多元函数的洛必达法则

曾玲莉，周雨佳

(西北大学 数学学院，西安 710127)

1 研究背景

1.1 洛必达法则

极限理论作为数学分析的理论基础，主要研究内容包含两个部分：首要任务是对极限能否存在，即存在性进行研究[1]，其次是求解极限的值。求极限值一直以来是众多学者探讨的问题，然而没有形成一致的方法和步骤，只能根据具体情况进行分析再采取合适的方法进行求解。求极限值的方法有许多种，大家熟知的有夹逼准则、单调有界原理、Stolz公式等，但最常用最简洁的是L’Hospital法则。

1.2 多元函数洛必达法则的发展背景

多元函数的极限有累次极限和重极限，因为函数自变量个数的增多，函数所处区域的不确定性，重极限变得十分复杂。求极限值，首先要保证这个极限是存在的，而关于多元函数的极限是否存在的问题便是一个难题，多元函数极限存在的条件比一元函数的洛必达法则更为严格。

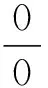
综上所述，现有研究主要是通过将多元函数不定式极限转化为一元函数或其他形式进行求解，很少有学者基于多元函数极限本身性质进行探究。

1.3 研究内容和目的

一元函数的洛必达法则在数学以及其他学科的运用中起到很大作用，无论是对于数学基础的建设，还是学生在考试中的应用上都十分重要。因此，对于多元函数的洛必达法则的研究具有重要意义，多元函数洛必达法则是否和一元函数具有相似的性质值得进一步探索。

本文在已有文献的基础上，总结了二元函数不定式的洛必达法则，并给出了二元函数洛必达法则的充分必要条件以及多元函数的洛必达法则，希望可以更便捷地求解多元函数不定式的极限值，丰富洛必达法则的内容，使洛必达法则的使用范围更加广泛。

2 预备知识

定义3[4]：设函数y=f(x)，若自变量在点x的改变量Δx与函数相应的改变量Δy有关系Δy=A×Δx+ο(Δx)，其中A与Δx无关，则称函数f(x)在点x可微，并称AΔx为函数f(x)在点x的微分，记作dy，即dy=A×Δx，当x=x0时，则记作dy|x=x0。

3 主要结果与证明

引理1[10]海涅定理

引理2[11]二元函数的柯西中值定理

设二元函数f(x,y)，g(x,y)满足以下条件：

(ⅰ)f(x,y)g(x,y)在去心矩形区域D:0<|x-x0|≤a,0<|y-y0|≤b内有连续的偏导数，且g1(x,y)dx+g2(x,y)dy≠0；

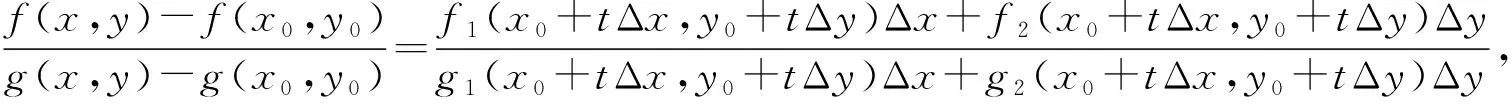
设二元函数f(x,y)，g(x,y)满足下列条件：

(ⅰ)去心矩形区域D:0<|x-x0|≤a,0<|y-y0|≤b内有连续的偏导数，且g1(x,y)dx+g2(x,y)dy≠0；

设二元函数f(x,y)，g(x,y)满足下列条件：

(ⅰ)去心矩形区域D:0<|x-x0|≤a,0<|y-y0|≤b内有连续的偏导数，且g1(x,y)dx+g2(x,y)dy≠0；

证明：

充分性：

必要性：

4 应用举例