计量学中浮点运算造成的痕量偏差对数据修约的影响及解决方案

毛森，王晓伟，杨宇，李光旭

(河南省计量科学研究院，郑州 450047)

电子原始记录数据的自动化处理功能不仅能够提高计量技术人员的工作效率，降低技术人员工作强度，还能够有效降低人工引入的差错率[1-2]。随着计量技术机构近年来的持续推广普及，电子原始记录在各计量仪器设备检定、校准过程中的使用覆盖率持续升高，技术人员对电子原始记录的依赖程度日益加深[3]。电子原始记录的实现方式有多种，从目前使用情况看，依托电子表格(以Excel 软件为代表)对原始数据进行处理的方案较为普遍和成熟[4]。计量学对计量数据的计算及修约精度有较高要求，数据修约需严格符合GB/T 8170 规定[5]。由于计算机程序是采用二进制的方式进行数据存储[6-8]，运算过程采用浮点运算方式进行[9-11]，这种计算方法会造成计算机计算结果与实际计算结果存在极为微小的偏差[12]。通常这种偏差对日常计算结果影响很小，但却会给计量结果造成不可忽略的影响，从而对仪器的级别判定造成本质影响。

综览国内外公开出版的学术期刊，尚未发现有研究这一现象和专门探讨数据自动化修约的报道。笔者以Excel 软件为依托软件，以两种典型的修约方法为例，介绍浮点运算造成的痕量偏差在修约过程中对数据结果的影响及规避方法。

1 修约方法中所用函数

使用Excel 处理数据时，采用自带的函数实现数据的修约，所用到的函数有IF()、Round()、MOD()、EVEN()、TRUNC()。以上函数的功能、各参数意义及使用规则见表1。

表1 Excel 部分函数用法及含义[13]

2 典型修约方法修约过程中的结果偏差现象与原因分析

2.1 数据自动修约典型

数据的修约是数据处理至关重要的一个环节，数据修约的正确与否直接关系到仪器准确程度的判断。在石油密度计检定过程中，经常需要对其修正值进行修约运算，通常Excel 在数据修约过程中采用“四舍五入”的进舍规则，这种修约规则并不能满足日常测量数据的处理要求。计量学中数字修约规则要符合GB/T 8170—2008 规定，即“四舍六入，逢五取偶”[14]，俗称“奇进偶不进”。要实现这种特殊的修约规则，则需要用到多种Excel 函数进行组合运算。

以下列举两种不同的方法对数据进行修约。

(1)方法一。具体实现过程：(为方便理解，默认对被修约数修约至个位)先使用ROUND 函数对被修约数进行四舍五入修约，再用返回值减去一个逻辑判断的返回结果(用MOD 函数以2 作为除数对被修约数除求余，当余数等于0.5 时返回1，否则返回0)。修约公式为：

ROUND(被修约数，有效位数)-(MOD(被修约数＊10^有效位数，2)=0.5)＊10^-有效位数

(2)方法二。具体实现过程：首先要对被修约数进行底数为10 的乘幂运算，将被修约位数移至小数点后一位，再用MOD()函数对被修约数进行除数为1 的求余运算。如果余数不为0.5，则对被修约数用ROUND()函数进行“四舍六入”运算；反之，则对被修约数先用TURNC()函数做取整运算，后用EVEN()函数做向上取偶运算，从而实现“逢五取偶”运算。修约公式：

IF(MOD( 被 修 约 数＊10^ 有 效 位，1)=0.5，EVEN(TRUNC( 被 修 约 数＊10^ 有 效 位 数，0))，ROUND(被修约数＊10^有效位数，0))/10^有效位数

修约公式中各参数含义参照表1。

表1 列举了3 种不同的修约公式是对固定数值的修约过程与结果，从结果不难判断，ROUND 函数仅能实现对固定值按照四舍五入修约规则进行修约，而以上两种修约方法能够实现对固定值按照“奇进偶不进”修约规则进行修约。

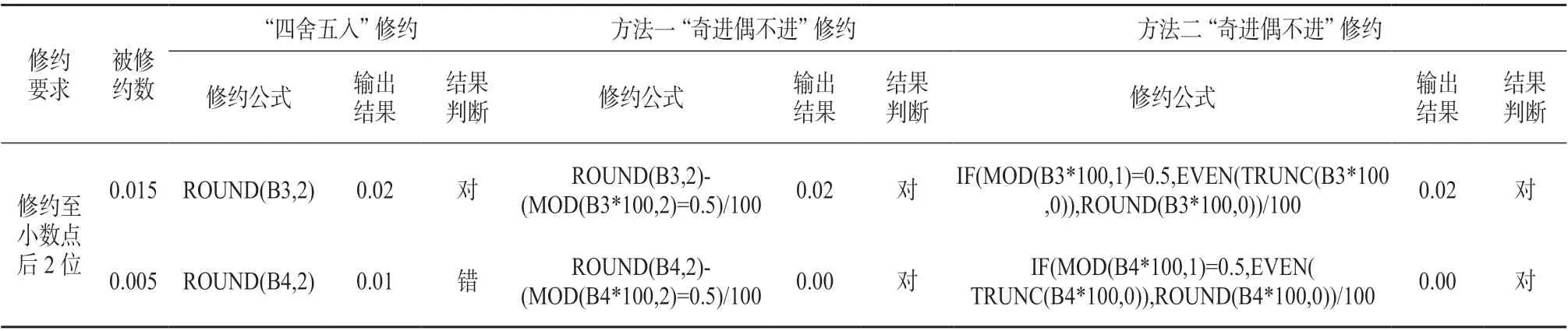
表1 三种修约公式对修约规则实现示例

2.2 浮点运算造成的痕量偏差对数据修约的影响

仪器准确度等级的判定需要对被检仪器的多项性能指标做出综合性判断才能得出。各项指标是通过原始记录中的数值按照规程给出的计算公式计算得出中间值，再对中间值进行相应的修约，最终才能得到用于判定级别的最终运算结果。

2.2.1 现象描述

以酸度计检定项目“电计输入阻抗引起的示值误差和近似等效阻抗”[15]项目为例：使用酸度计检定仪(标准信号发生器)向被检酸度计发送pH 13.000 的信号，酸度计在串联3×109Ω 电阻前后，pH 示值分别为13.00 和13.03，ΔpHR为0.015，按照“四舍五入”的修约规则将ΔpHR修约至小数点后2 位，pH 结果应为0.02，而用方法一和方法二进行修约实际得到的pH 结果均为0.01，软件修约结果明显发生了错误；而使用酸度计检定仪向被检酸度计发送pH 1.000 的信号，酸度计在串联3×109Ω电阻前后，pH 示值分别为1.00 和1.01，ΔpH'R为0.005，按照“奇进偶不进”的修约规则将ΔpH'R修约至小数点后2 位，结果应为0.00，用方法一、方法二分别对ΔpH'R进行修约得到的结果亦为0.00，软件修约结果与人工计算结果又保持了一致，如表2所示。综上，采用方法一和方法二对两个采用相同计算公式产生的中间值进行修约时，却出现了两种不同的结果。

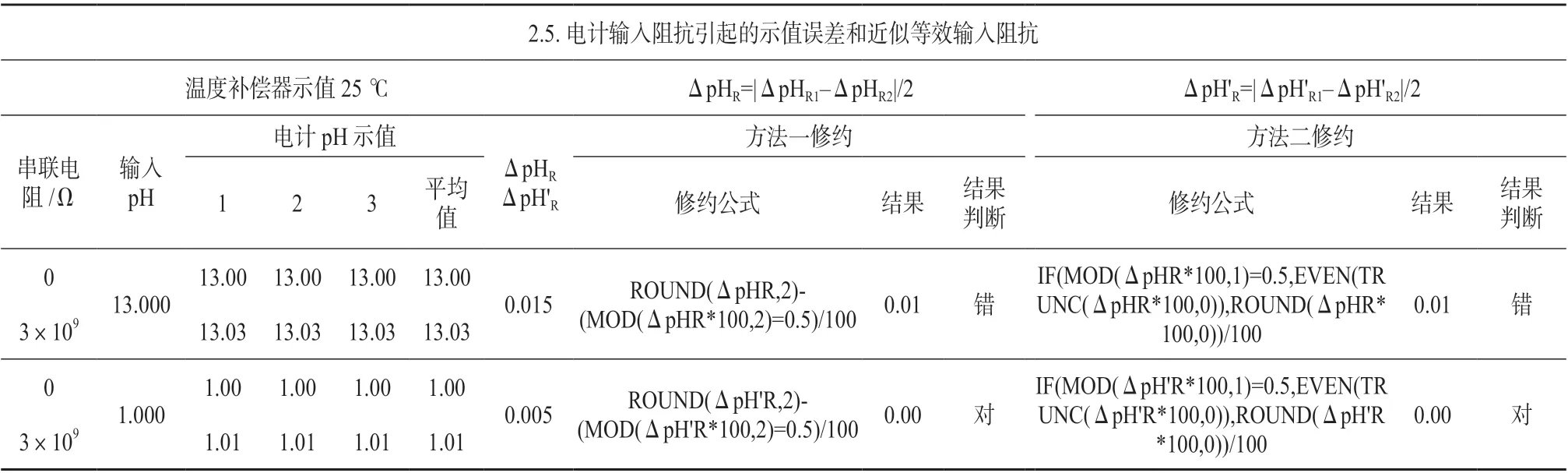
表2 在酸度计电计输入阻抗引起的示值误差中由于浮点运算造成修约结果错误的示例

2.2.2 原因分析

计算机采用浮点运算进行数据处理，采用二进制对数据及运算结果进行存储。在使用Excel 软件对十进制数据运算时，计算机需要将每一个十进制数值转化成二进制字符存储，然后对存储值进行运算，运算完成后再将存储的二进制结果转化成十进制结果进行显示，数据转换存储过程中有可能造成极其微小的折损，从而造成最终的修约结果错误(见表2)。

利用如下试验证实以上推论：用计算显示(存储) 值(ΔpHR、ΔpH’R) 与 实 际 值(0.015、0.005)作减法运算，验证计算显示值(即存储值)与实际值是否一致，示例如表3。从表3 中不难看出，ΔpH’R的存储值与实际值0.005 差值为0，说明两者是一致的。而ΔpHR的存储值与实际值0.015 差值为-3.19189×10-16。这证明了被修约数ΔpHR存储值与显示值存在痕量的偏差。

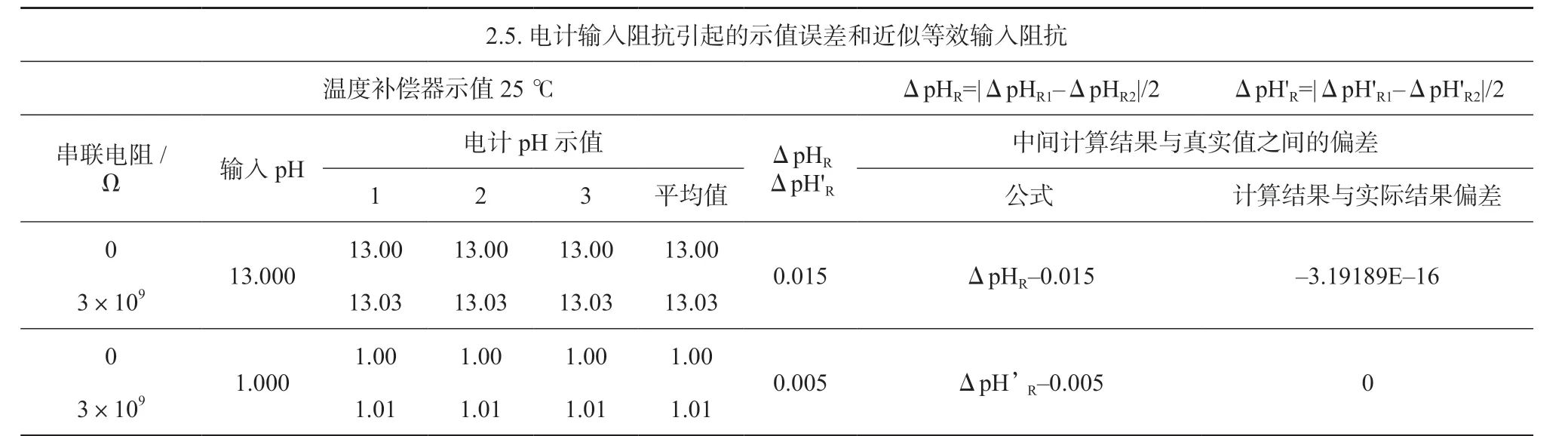
表3 计算机软件的显示值与实际值存在的微小偏差示例图

综上，浮点运算造成的痕量偏差具有一定的随机性，并不总是存在的。这种偏差对于粗略的运算影响不大，但在精密的计量数据处理过程中，会对后续数据处理过程产生叠加影响，从而导致了整体结果的偏离，最终致使仪器判定级别出现错误。

2.3 增加修正值以规避浮点运算对修约过程的影响

针对2.2 中所提到的问题，可以根据其特点，化不确定问题为确定问题。假设痕量偏差一定存在，以此为前提，在被修约的中间值中增加修正值，把单点判断变为范围判断，从而将浮点运算造成的痕量偏差消除。仍以2.2 中所举示例为例：按照2.1“方法一”中的描述，对单元格“ΔpHR”存储数据进行修约(“四舍六入，逢五取偶”规则)时，需要考虑到痕量偏差造成的两方面影响：一方面是对Round函数修约的影响，另一方面是对Mod 函数逻辑判断的影响。针对前者，可假设单元格“ΔpHR”中存储的计算显示值一定存在痕量偏差，在采用Round 函数进行修约之前，对单元格“ΔpHR”存储值加上已知微小数(例如0.000 001)，以确保“四舍五入”修约规则的实现；针对后者，可对单元格“ΔpHR”存储值求余运算结果与预期结果进行差值运算，如果存储值无限接近预期值，则二者差值应接近于0，可以预判其必定小于一个既定值(例如0.01)，以此将单点逻辑判断变为范围判断，从而消除痕量偏差造成的影响。具体过程如表4 所示。

表4 改进前后的修约公式输出结果对比图

通过表4 中改进前后的修约结果对比不难判断，修约公式在改进前，受到浮点运算造成的痕量偏差的影响，其输出值有对有错，也就是说其修约结果的可信度很差，如果以此作为仪器级别判定的标准，可能会产生错误结果。而通过改进修约公式，其结果的正确性得到了保证，证明上述改进方案是可行的。

3 结论

用计算机做数据处理时，计算机的浮点运算及二进制存储过程会对计算结果产生微小影响，这种影响具有一定的不确定性并且会累积，通常情况下，不会对复杂的中间运算结果修约造成干扰，但在一些特殊情况中，会导致数据修约结果错误，从而对一些特殊行业产生较大的影响。通过用范围判断取代单点判断的方法可以消除这种影响，较好的规避数据浮点运算及二进制存储对修约过程造成的干扰，从而保证修约结果的准确。由于数据处理具有复杂性，文中所给方法并不能解决所有计算机浮点运算造成的干扰，遇到具体问题仍需要对症下药，给出合适的预判方案以规避风险，期望越来越多的实用技巧被计量相关从业人员开发并推广。另外，根据GB/T 8170—2008 规定，按照修约间隔不同，还可分为0.1 间隔修约、0.2 间隔修约、0.5 间隔修约[16-17]。在具体的数据修约过程中，还要结合不同的修约间隔对数据作出精细化的分析。数据处理作为检测能力的一种具体体现，其与信息化技术相结合是提高检测能力的有效途径。对数据自动化处理中隐藏的问题进行深入挖掘分析，有助于提高计量检测精度，规避行业潜在风险，具有十分重要的现实意义。