红石岩堰塞坝力学参数随机场模拟研究

贾 宇 峰，葛 培 杰，相 彪，陈 永 康

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024； 2.大连理工大学 工程抗震研究所，辽宁 大连 116024； 3.云南农业大学 水利学院，云南 昆明 650201)

0 引 言

2014年8月3日，在云南省鲁甸县和巧家县交界处发生了6.5级地震。地震导致鲁甸县火德红乡红石岩村的牛栏江干流两岸发生大面积的山体崩塌和滑坡。地震引发的滑坡形成了顺河向长约1 807 m，高103 m，宽307 m，体积约1×107m3的堰塞体，如图1所示。从图中可以看到，堰塞体左岸侧为古滑坡体，河谷中心处为新堆积体，底部为河床冲积层。由于左岸古滑坡体稳定性较差，采用爆破方式拆除堰塞体极易引发次生灾害。并且，堰塞体体积巨大，采用常规方式进行拆除不仅需要对上部古滑坡体进行加固处理、设计合适的排渣场地，还需要承担高额的运输费用和较长的处理时间。因此，通过在堰塞体中设立混凝土防渗墙和帷幕灌浆区，可将其改建为永久性挡水建筑物，从而建成红石岩堰塞湖多功能大型综合水利枢纽工程。其中，堰塞坝最大坝高103 m，库容2.6亿m3，达到大(2)型水库规模。由图1可以看到，地震引起滑坡形成的新堆积体位于河道中央，是堰塞坝防渗墙所在区域。为了准确分析新堆积体的力学参数特性，预测坝体变形，分析混凝土防渗墙的变形和应力分布特性，对堰塞坝新堆积体进行了详细的现场勘察。

图1 堰塞体现场Fig.1 Photo of the barrier dam

现场勘察结果表明，红石岩堰塞坝新堆积体主要由弱风化、微新风化和新鲜的白云岩和灰岩组成。新堆积体上部18～40 m为孤石和块石，夹杂少量碎石和砂；下部以块石、碎石混合砂土为主。新堆积体上部细颗粒较少，存在架空现象，密度较低，下部颗粒级配基本连续，孔隙率低，密实度较高，变形模量较高。表1中列出了7次现场密度试验的测量结果。图2给出了现场钻孔试验测定的不同位置新堆积体的颗粒级配和相应的采样位置分布和采样点高程。

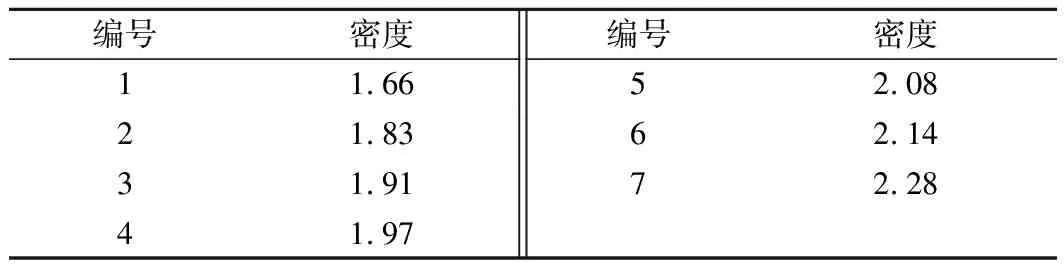
表1 堆积体现场密度采样结果Tab.1 Field results of accumulation body density g/cm3

图2表明新堆积体上游侧表面区域(ZK133，埋深9.5～12.6 m)粗颗粒较多，1 mm以上颗粒百分比超过74%。在新堆积体中部(ZK109-2，埋深46.3～47.9 m)的中间区域，小粒径颗粒含量明显提高，1 mm以下颗粒含量超过40%，在下游侧底层区域(ZK101-2，埋深 54.7～56.3 m)小颗粒含量更高，1 mm以下颗粒含量超过 50%。为了确定新堆积体颗粒的力学特性，进行了15组随机取样的岩石单轴抗压强度试验和4组直剪试验。试验结果表明，由于岩石风化程度不同，室内试验的单轴抗压强度差异性较大。干抗压强度在27.0～192.8 MPa，湿抗压强度在18.0～169.1 MPa，岩石抗剪角度在53.2°～61.7°，黏聚力在5.0～5.61 MPa。

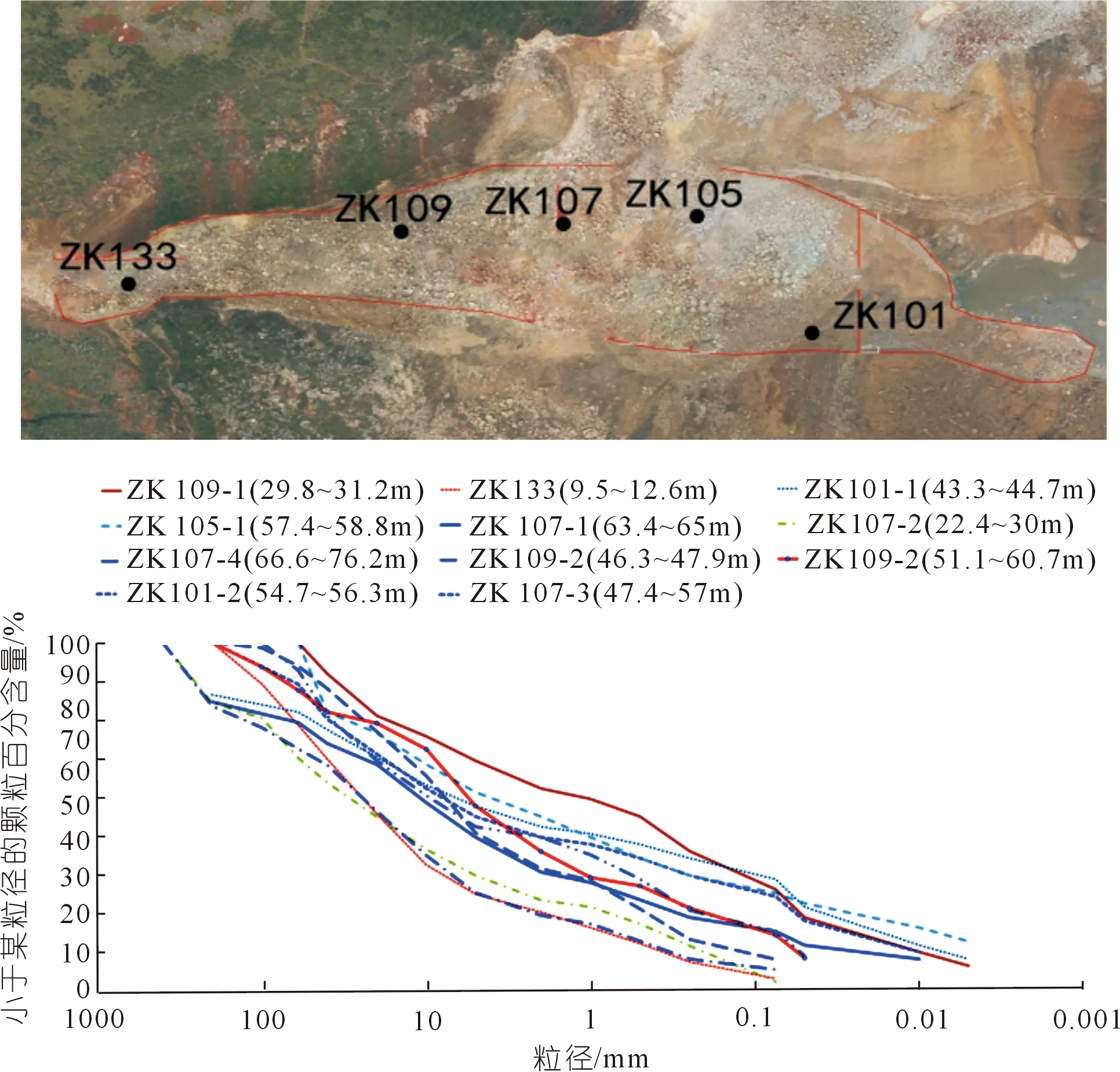
图2 现场钻孔试验采样位置与试样颗粒分布Fig.2 Sampling location and particle distribution of field borehole test

新堆积体的现场试验结果表明：新堆积体的密度分布规律具有明显的离散性；新堆积体的颗粒组成呈现显著的空间变异性，并且其小颗粒百分比远高于土石坝的堆石料，其大颗粒粒径又明显超出心墙掺粒料范围；并且土颗粒由白云岩和灰岩混合构成，颗粒风化程度差异导致其强度存在较大的离散性。传统的均质材料数值模型无法描述新堆积体力学参数的空间变异性。因此，本文根据空间随机场理论，结合现场试验和室内三轴试验构建了红石岩新堆积体力学参数的随机场有限元模型，为红石岩堰塞坝安全分析奠定了基础。

1 随机场理论的基本概念

空间变异性是天然土体固有的一种属性。地震引起山体滑坡形成的红石岩新堆积，其土体参数分布具有明显的空间变异性。已有研究结果表明，自然土体的密度和强度参数的分布规律可以采用标准正态分布或自然对数正态分布描述[1]。在此基础上，根据现场观测数据，通过相关函数来描述土体内部不同空间坐标下的土体参数之间的相关性，建立描述土体参数空间变异性的随机场有限元模型。

1.1 随机场的构建

目前，建立随机场有限元模型的成熟方法有Karhunen-Loeve级数展开法[2]、协方差矩阵分解法[3]等。上述离散方法在边坡稳定性、盾构隧道变形分析方面应用较广。如李典庆[4]、蒋水华[5]等学者采用Karhunen-Loeve级数展开法构建了土坡强度参数的随机场，进行了土坡可靠度分析。袁葳等[6]学者则采用Karhunen-Loeve级数展开法描述土体内摩擦角和黏聚力的空间变异性。程红战等[7]学者则采用协方差矩阵分解法模拟土体弹性模量变异性，进行盾构隧道数值分析。李健斌等[8]学者则对采用Karhunen-Loeve级数法建立的盾构隧道随机有限元模型的力学响应进行了敏感性分析。然而上述Karhunen-Loeve级数离散方法在针对不规则区域时，第二类Fredholm方程求解相对较难实现。而基于Cholesky分解的协方差矩阵分解法可适用于不规则区域且编程较为简单，便于工程应用。另一方面，随机场理论在土石坝安全评价分析方面应用较少。杨鸽等[9]学者提出考虑力学参数的空间变异性的土石坝动力分析结果明显有别于传统的确定性方法。

综上所述，本文根据红石岩堰塞坝现场试验确定新堆积体力学参数的相关距离，采用高斯函数拟合坝体内各个单元之间的相关系数，通过室内三轴试验确定力学参数的统计规律。采用协方差分解法建立堰塞坝新堆积体随机有限元模型。

1.2 协方差分解法

堰塞坝新堆积体有限元模型中，任意两个单元i和单元j之间的土体参数相关性可以采用三维高斯型相关函数描述，其表达式为

(1)

式中：τx、τy、τz表示i单元和j单元形心在x、y、z3个方向的距离；δx、δy、δz为3个方向的相关距离。由式(1) 可以求出坝体内任意两个单元参数之间的相关系数(aij=ρij)，组成对称正定的n阶相关系数矩阵A，对A矩阵进行三角分解，可得：

A=LLT

(2)

其中，L为下三角矩阵。新堆积体随机场有限元模型中，n个单元土体参数为

H(X)=μ+σLZ

(3)

式中：H(X)是n阶参数向量，且X={(xi，yi，zi)，i=1，…，n}代表n个单元的形心坐标，Z是代表不同位置单元土体参数分布概率的n阶独立标准正交随机向量，μ和σ分别为新堆积体参数的平均值和标准差。因此，由(3)式确定的新堆积体参数向量H符合各个单元之间的相关性，并且其统计参数也收敛于现场试验和室内三轴试验确定的统计值。

2 新堆积体参数相关距离的确定

2.1 空间递推法

土体参数的相关距离δ是描述其空间分布规律影响范围的参数，反映了不同方向上土体结构的变化程度[10]。本文通过空间递推法计算相关距离[11]。空间递推法通过方差折减函数Γ2(h)与土体参数样本波动范围h的关系计算相关距离。其基本步骤是将h取为取样间距Δz的倍数，即h=iΔz(i=1，2，3…)，然后将相邻i个数据点构成一组新的样本，计算新样本的方差为γ2(h)，S2为初始样本数据的方差，那么方差折减函数为

(4)

2.2 根据现场试验确定相关距离

红石岩新堆积体由地震引发山体滑坡形成，无法通过坝体内各个高程不同位置测量的密度或孔隙比等参数计算相关距离。因此，本文通过现场勘察试验测量的剪切波速、表面波速和视电阻率计算相关距离。图3给出了部分测点的竖直向剪切波速沿深度的分布图。图4～5给出了两个顺河向剖面的表面波速和视电阻率分布情况。以竖向相关距离计算为例，主要计算步骤如下：

(1) 先对图3中竖向剪切波速的样本数据进行趋势项分解，建立趋势项参数沿竖向分布的经验公式。并在此基础上，从实测剪切波速中扣除趋势项分量，确定由随机项分量产生的方差S2。

(2) 根据现场实际采样数据点的间距值Δz估算数据的波动范围h，即h=iΔz。以临近的i个数据点的剪切波速作为一组新样本，求出该组数据的方差γ2(h)。

(4) 绘制方差折减函数与波动范围的分布曲线，即Γ2(h)～h图。

(5) 根据所建立的Γ2(h)～h分布曲线，确定方差折减函数值趋于平稳的波动范围值h=i*Δz，根据δu=i*ΔzΓ2(i*)确定剪切波速的相关距离。

图4 顺河向剖面表面波速分布(单位：m/s)Fig.4 Surface wave velocity distribution of a section along the river

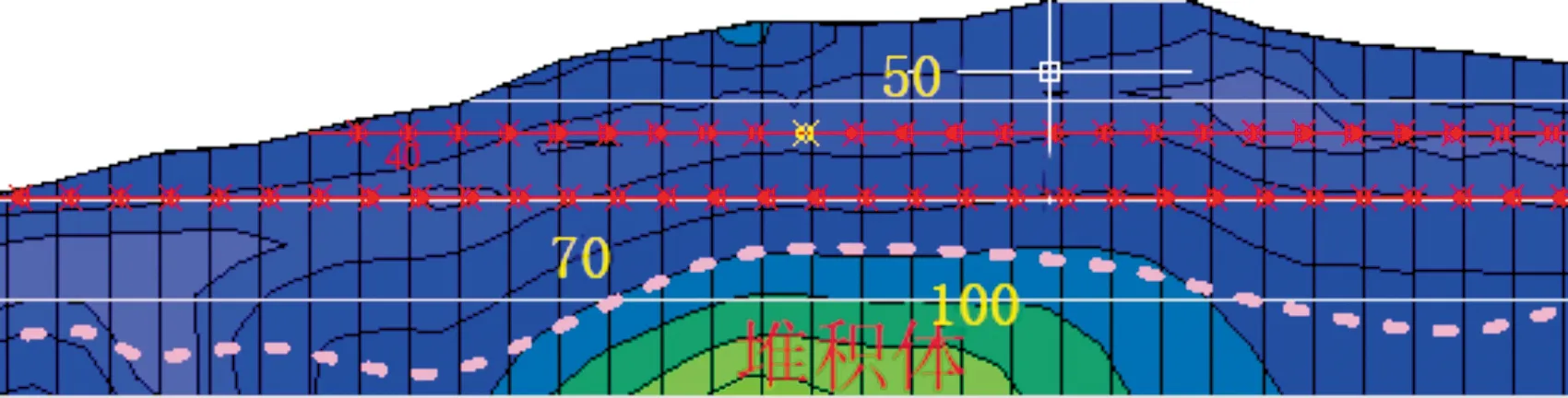
图5 顺河向剖面视电阻率分布(单位：Ω·m)Fig.5 Apparent resistivity distribution of a section along the river

已有研究结果表明，土体参数的相关距离可用来表征采样范围内不同位置土体参数之间的互相关性。因此，相同土层中剪切波速确定的相关距离同样也可以用于描述其它土体参数的互相关性[12]。新堆积体的水平相关距离也可以采用上述方法由图4～5中的实测表面波速和视电阻率确定。各个方向上的相关距离如表2所列，水平向相关距离取两种现场数据的计算结果的平均值(33.94 m)。

根据竖向相关距离和水平相关距离，结合式(1)可以求出新堆积体内各个位置点的力学参数在竖直向和水平向的相关系数。进而构建符合现场地勘实验数据分布规律的力学参数随机场。

表2 红石岩新堆积体物理参数的相关距离Tab.2 Correlation distance of Hongshiyan new accamulation material m

3 新堆积体力学参数的统计规律

3.1 试验方案

新堆积体力学参数的统计规律根据室内常规三轴试验确定。将红石岩新堆积体的现场采样级配通过等量替代法进行缩尺，拟定具有代表性的3条级配曲线，即上包线级配、平均线级配和下包线级配作为室内试验级配，如图6所示。

图6 三轴试验级配曲线Fig.6 Triaxial test grading curve

通过现场7次密度试验，拟合得到新堆积体的密度分布曲线(均值为1.98 g/cm3，标准差为0.21)。结合密度的正态分布特征和室内试验实际情况，确定室内试验密度为2.28，2.17，2.06，1.95，1.84 g/cm3，如图7所示。在试验级配和密度确定之后，分别进行围压为400，800，1 200 kPa的多组室内固结排水三轴压缩试验，试验方案见表3。

图7 室内试验密度确定Fig.7 Determination of laboratory test density

表3 室内三轴压缩试验方案

3.2 力学参数统计分析

按照表3的方案进行三轴试验，典型的三轴试验结果如图8所示。邓肯E-B模型能够较好地描述土体的非线性力学特性，广泛应用于土石坝数值分析，是目前SL 274-2020《碾压式土石坝设计规范》推荐的土石料本构模型。根据三轴试验结果整理了各个试验方案下的邓肯张E-B模型参数列入表4中。

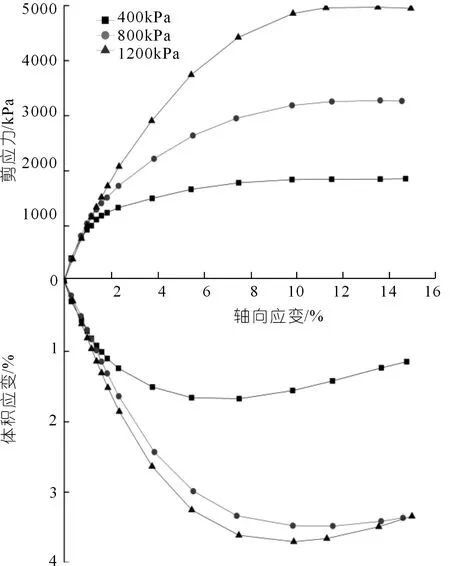
图8 试验方案7的三轴试验曲线Fig.8 Triaxial test curve of Test 7

由于E-B模型参数中，K、n、Kb和m是影响土石坝静力分析的主要参数。因此，本文仅构建了上述4个参数的随机场有限元模型。为了确定参数分布规律，对上述4种参数的试验数值进行了K-S检验[13]。K-S检验法将数据样本的累积频数函数与理论分布函数差异的最大值D作为衡量样本分布规律的统计量。表5给出了4个参数的D值，而D7，0.05为0.483 4。可以看到，根据对数正态分布计算的D值均小于分位值0.483 4，参数服从对数正态分布。这主要是因为邓肯E-B模型参数在数值上都是正值，并且模型数值的分布离散性较大，其原因是粗粒含量对模型的力学特性存在较大影响，相同密度条件下随着粗颗粒含量的增大模型参数变化幅度较大。

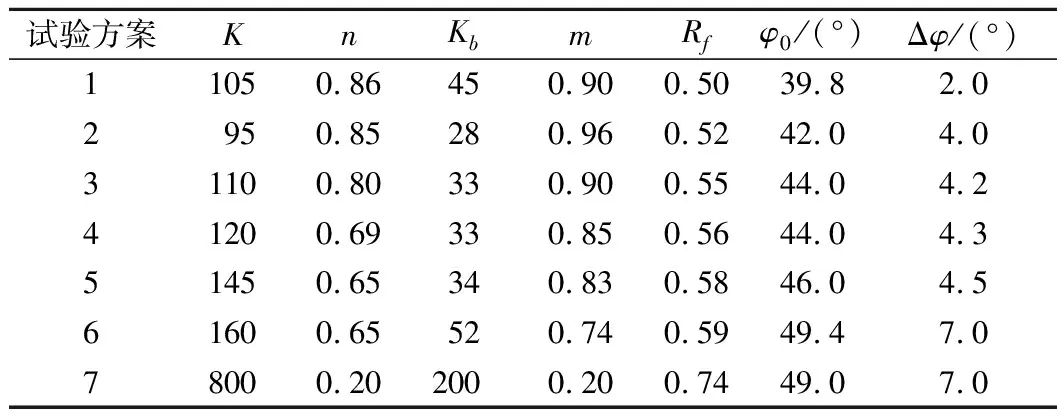
表4 新堆积体E-B模型参数Tab.4 E-B model parameters of new accumulation body

表5 模型参数统计规律Tab.5 Parameter statistical characters

4 新堆积体力学参数随机场的构建

红石岩堰塞坝三维有限元模型如图9所示。有限元模型中单元数为10 083，节点数为8 579。

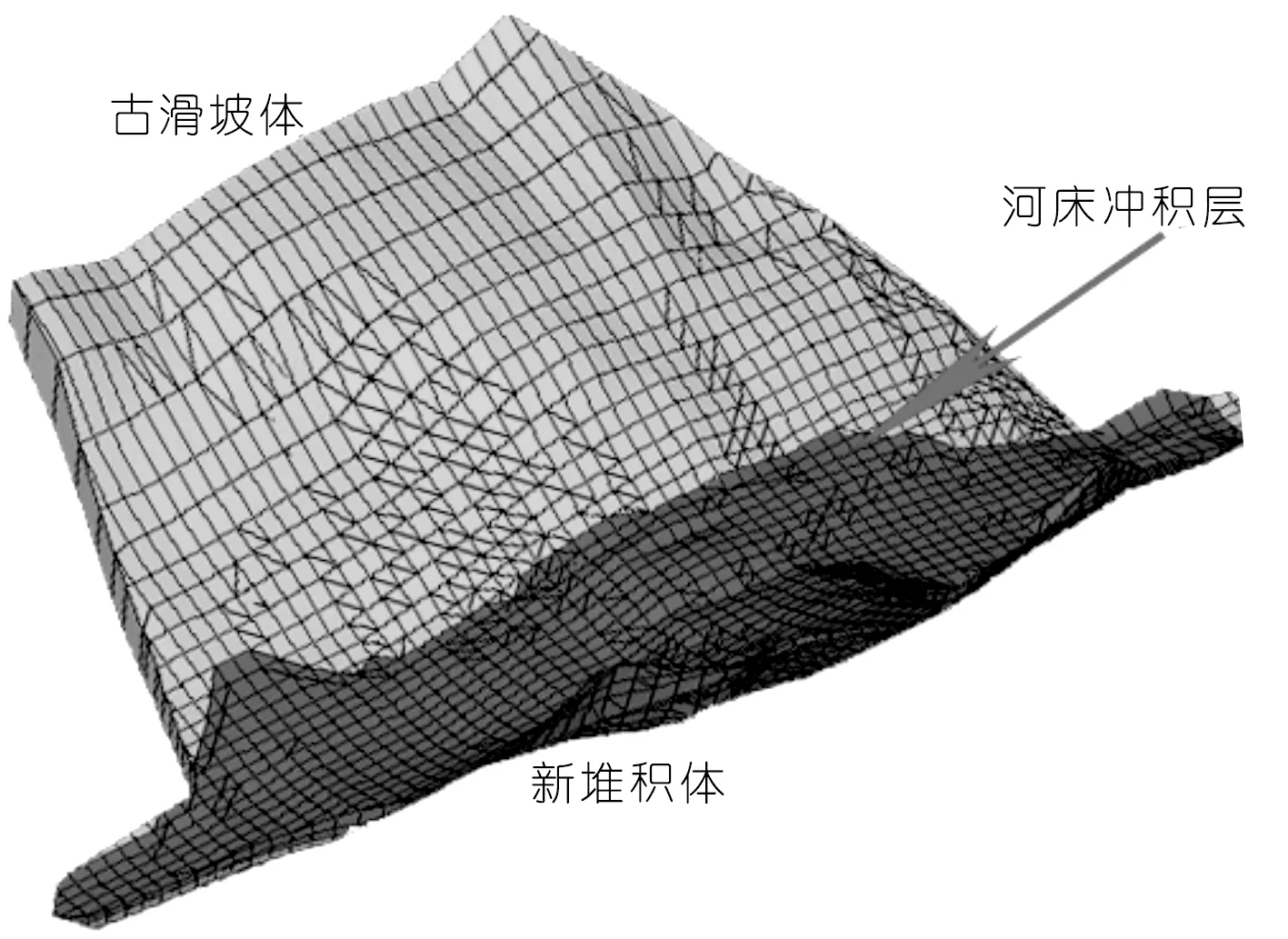
图9 红石岩堰塞体三维有限元模型Fig.9 Three-dimensional finite element model of Hongshiyan barries dam body

参数K、Kb、n、m均服从对数正态分布，而协方差矩阵分解法是在标准正态空间下进行的。因此，需要将标准正态空间变换到对数正态空间。对H取对数[8]，便可得出对数正态分布下的空间随机场He：

He=exp(μln+σlnLZ)

(5)

(6)

式中：μln和σln为对数正态分布下参数的平均值和标准差。

根据式(5)，结合所建立的红石岩堰塞坝三维有限元模型，生成新堆积参数的随机场有限元模型：

(1) 采用拉丁超立方抽样方法随机产生一组独立标准正态随机向量Z。

(2) 根据有限元模型中各单元形心点的空间坐标Xi(i=1，2，…，10 083)，采用表2中的相关距离，根据式(1)求出新堆积体有限元模型的相关系数矩阵C，并进行三角分解，得到系数矩阵L。

(3) 根据式(6)求出对数正态分布下的平均值μln和标准差σln。

(4) 根据式(5)求出新堆积体单元各个参数的随机场He。

图10和图11为参数K的某次随机抽样结果在典型断面的分布情况。参数Kb、n、m的随机场实现与参数K类似，由于篇幅有限暂未列出。

图10 顺河向剖面K参数随机场分布Fig.10 Distribution of K parameter random field along the river section

图11 横河向剖面K参数随机场分布Fig.11 Distribution of K parameter random field along the dam axial section

5 结 论

本文根据红石岩堰塞坝新堆积体现场试验资料，结合7组室内三轴试验结果构建了K、n、Kb、m参数的随机场模型，从中得出一些有益的结论：

(1) 通过空间递推法依据现场剪切波速求出红石岩堰新堆积体竖向相关距离为2.84 m，根据现场表面波速和视电阻率求出新堆积体水平相关距离平均值为33.94 m。

(2) 室内试验参数结果经K-S检验后，发现新堆积体邓肯张E-B模型参数K、Kb、n和m符合对数正态分布规律。

(3) 采用平稳性较好的高斯相关函数构建的协方差矩阵能够有效地描述红石岩新堆积体力学参数的空间变异性。