分形流场传质输运特性的数值模拟研究
石 均,陶善聪,周 毅
(1.南京理工大学能源与动力工程学院,江苏 南京 210094;2.中国航天空气动力技术研究院,北京 100074)
湍流现象广泛存在于自然界和工业界中,如森林火灾的大规模传播[1,2]、城市热岛效应[3]、发动机燃烧室的湍流燃烧[4]、机翼尾流[5]等.根据已有研究表明,湍流可以提高流动系统的输运能力和扩散混合强度[6].近些年,众多学者采用不同的方式来研究各种湍流问题.其中较为典型的是利用仿生学思想[7],提出将分形理论[8]与湍流领域相结合,从而来探索更为复杂的湍流现象,以期为实现相关的工业应用提供理论指导.
分形网格湍流FGT(Fractal-Generated Turbulence)是流体流过具有分形特征的格栅时引发的不规则、混乱的流动现象,如上文提到森林火灾的扩散呈现出分形湍流的特点[1,2].与之对应的则被称为规则网格湍流RGT(Regular-Generated Turbulence),即流体流经具有规则结构的格栅后产生的湍流现象.此前,经研究发现分形流场具有比规则流场更强的湍流扩散混合能力[9],为此人们对这种分形湍流过程的研究热度与日俱增.Queiros-Conde等[10]早期便是利用在风洞中加入分形格栅来开展分形流动研究,结果发现分形流动的结构函数尺度指数变化趋势与分形维度大小相反.Staicu等[11]利用分形流动实验探索了惯性尺度和耗散尺度范围内的流场特点,证明分形湍流的自相似性行为受到分形结构维度的影响.Hurst和Vassilicos[12]开展分形湍流实验,对比了十字形、工字形和正方形三种网格形成的湍流场特性,结果发现流场下游的均匀各向同性取决于分形结构的几何维度或网格的尺寸.Seoud和Vassilicos[13]对上述几种网格湍流进行了更深入的研究后发现,在远离网格的流场下游衰减区域,泰勒微尺度与积分尺度的变化保持相对独立,并与入口初始速度无关.Laizet和Vassilicos[14]采用直接数值模拟DNS(Direct Numerical Simulation)手段对FGT和RGT进行仿真研究,发现分形流场具有更高的涡度和湍流强度.Laizet等[15,16]利用高保真数值方法Incompact 3D对FGT进行一系列研究后指出,在分形流场远下游区域的小尺度尾流会被随机卷入大尺度尾流中,并且不停地重复这种行为.因此他们认为是特殊的分形结构导致了分形流场的标量输运和扩散能力更强,同时据此提出了一种空间尺度展开SSU(Space-Scale Unfolding)机制.此后,Laizet和Vassilicos[17]开展了二维分形湍流的数值模拟,证实了由于SSU机制导致分形流场的标量横向扩散能力大于规则流场.另外,特别是近年来,大量学者积极探索分形湍流理论的其他应用可能性.例如,Cafiero等[18,19]基于分形网格增强射流湍流强度的原理进行实验研究,提出了一种圆形冲击射流被动强化传热的新方法.Paul等[20]对单一方形结构湍流场开展DNS研究,通过对Nusselt的统计分析发现,与前沿驻点相比,流场最大热传递点附近发生了极端事件.并且他们建议可以将相应的研究结果应用于换热器传热优化等实际问题.Hoi等[21,22]将分形结构应用于翅片散热器中,在换热器领域取得了大量研究成果.Gehlert等[23]将分形端板引入到NACA0012半翼展中进行飞行实验,结果发现分形端板对翼尖涡结构和尾流场特性产生了较大影响,这意味着可将分形结构应用于飞行器部件设计中.
此外,分形结构提高湍流扩散混合能力的特点在诸多工业设备中具有广泛应用潜力,如采用分形刀刃的搅拌器[24]及燃烧设备中设置分形结构[25]等.然而,经过文献分析发现,大量学者关于分形流场的研究大都集中探索湍流统计特性的机理方面,尚未有学者对分形流场的传质输运特性进行深入分析.因此,本研究在课题组前期工作[26]的基础上,拟针对分形流场的输运机理开展研究.本文基于伪谱Fourier-Galerkin方法,将分形湍流按时间演化方式进行直接数值模拟.当分形流场演化至一定状态后,采用拉格朗日追踪方法,研究流场中流体微元的运动规律.同时模拟了具有相同阻塞率的RGT,以作对比分析.
1 直接数值模拟的方法简介
1.1 数值模拟的控制方程与数值方法
本研究的DNS仿真采用Hussaini等[27]提出的伪谱方法,流场在物理空间的控制方程包括连续性方程和Navier-Stokes方程(简称NS方程),如公式(1)和公式(2),其中空间网格节点进行均匀离散.
∇·u=0,
(1)
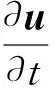
(2)
公式中:u为瞬时速度矢量;ν为运动粘度;P=p+u·u/2为无量纲化后的压力值.
在伪谱伽辽金方法中,需要将变量进行离散傅里叶变换至谱空间求解,因此控制方程最终在谱空间的为公式(3)和公式(4),具体的求解过程见参考文献[26].
(3)
(4)

本研究数值方法的时间递进采用四阶龙格-库塔格式.根据显示格式要求库朗数CFL(Courant Friedrichs Lewy)小于1,设置时间步长为Δt=0.005M/U0(M为规则相邻网格条之间的间距,同时也等于分形网格第三阶正方形的长度尺寸;U0为流场流向的初始平均速度).此外,NS方程的对流项、粘性项和压力项均采用谱方法求解.
1.2 计算域的参数设置
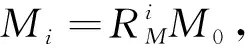
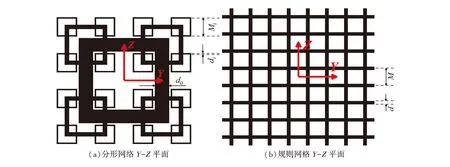
图1 分形网格与规则网格Y-Z平面示意图
此外,下面将给出数值模拟的部分参数,具体如表1所示.

表1 计算工况参数
两类流场网格在Y-Z平面上用Nf表示几何维度,规则网格的Nf=1,而分形网格的Nf=3(分别对应i=0,1,2).网格阻塞率为σ=Tbar/(LYLZ),Tbar表示Y-Z面网格条面积,LY和LZ分别为流场沿法向和展向的长度.本研究流场计算域的长度Lx=LY=LZ=8M.雷诺数设置为1 600,ReM=(U0M)/ν基于初始平均速度U0和网格尺寸大小M.将最大正方形网格的横向厚度与最小正方形横向厚度的比值定义为分形网格横向厚度比Dr,即Dr=d0/d2=9.5.
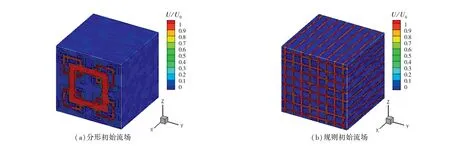
图2 加入附加扰动后的流场初始状态
此外,沿着流向X、法向Y和展向Z的网格节点数设置为Nx×NY×NZ=800×400×400,三个方向的节点为均匀布置,同时在X、Y和Z方向均采用周期性边界条件.其余具体的流场设置细节可参考文献[26],同时该文章中已经给出了FGT和RGT时间演化的初始速度条件.由于网格湍流的时间演化过程中需要向初始流场加入附加扰动,才能加速网格条产生的尾流从层流演变为湍流.本文FGT和RGT初始流场中添加的附加扰动场的脉动速度值大约为0.5%U0,特征长度尺度约为0.2M.将此附加扰动速度加入流场后,形成了两类网格湍流的初始状态,如图2所示.此外,关于数值方法准确性验证等方面的内容详情亦可参考文献[26],在此不再赘述.
2 粒子追踪期间的流场特性简介
流场演化至一定状态后,选取统计时间段为0≤Ttrack≤100Tr,主要研究流体微元的运动规律,下标“track”代表追踪粒子的含义.为了便于表述,后文统一将统计示踪粒子运动的初始时刻定义为Ttrack/Tr=0,结束统计的时刻定义为Ttrack/Tr=100,Tr=M/U0为无量纲化时间.需要明确的是,其中统计示踪粒子运动的初始时刻Ttrack/Tr=0并不等同于图2所示的流场初始演化时刻.因此,接下来首先对0≤Ttrack≤100Tr范围内的流场进行初步的介绍,旨在更清晰认识此时间段内流场的具体特征.
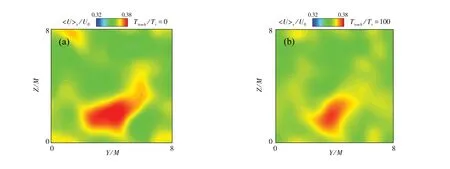
图3 不同统计时刻下FGT的流向平均速度云图
2.1 流向平均速度场
图3和图4分别为FGT和RGT在不同统计时刻下的流向平均速度〈U〉x云图,选取了Ttrack/Tr=0和100时刻的结果进行展示,符号“〈⋅〉x”表示对X方向进行平均.对于图3(a)的FGT而言,当Ttrack/Tr=0时,尽管分形流场Y-Z平面上整体的流向平均速度满足〈U〉x/U0≈0.36,但明显存在大尺度结构的痕迹,这说明此时的流场依然受到第一阶最大分形网格的影响.随着时间的演化,在图3(b)的Ttrack/Tr=100时,该大尺度结构的痕迹逐渐弱化,但其并非位于流场的中心区域,而是运动到了靠近流场的边界处.针对图4的规则流场演化结果,可以看出Ttrack/Tr=0至Ttrack/Tr=100,规则流场中几乎不存在大尺度痕迹,而且整个Y-Z平面的流向平均速度满足x/U0≈0.36,达到了较为均匀的状态.所以对比图3和图4可知,在统计时间(0≤Ttrack≤100Tr)内,分形条件依然影响着流场的发展状态.
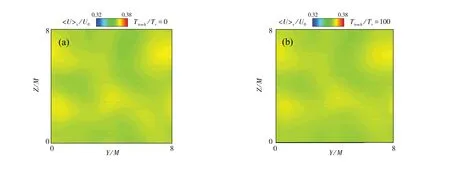
图4 不同统计时刻下RGT流向平均速度云图
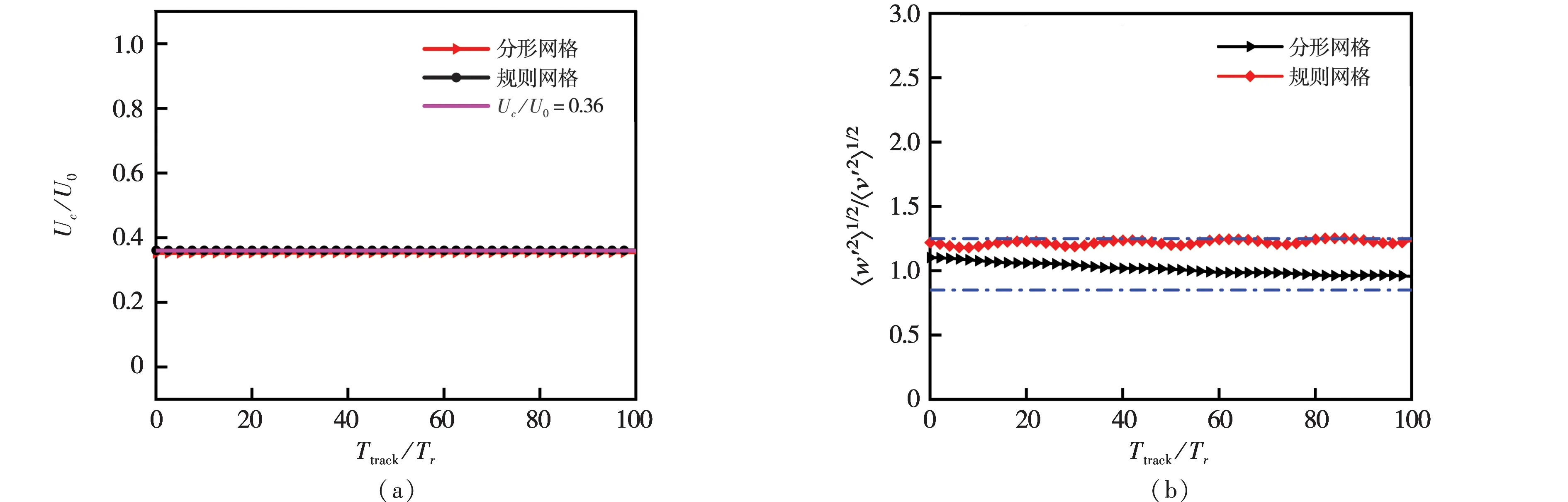
图5 流场的统计特性随时间演化结果
图5(a)为流场中心线上的流向平均速度Uc随时间演化结果,统计时间段内的FGT和RGT均满足Uc/U0≈0.36,因此流场沿流向发展基本趋于统计均匀,其中下标“c”代表流场中心线.根据课题组前期文章[26]的研究可知,初始条件对流场的影响消失后,整个流场都将演化至近似均匀各向同性状态.图5(b)为统计时间(0≤Ttrack≤100Tr)内流场展向与法向脉动速度比值,可以发现FGT和RGT两者的〈w′〉1/2/〈v′〉1/2均在0.85~1.25之间波动,符号“〈⋅〉”表示对X、Y和Z三个方向进行空间平均.其中,FGT的〈w′〉1/2/〈v′〉1/2比值从1.1开始随时间减小,而RGT的〈w′〉1/2/〈v′〉1/2在1.2附近徘徊.Laizet和Vassilicos[14]进行的FGT和RGT空间演化研究中也观察到,具有相同阻塞率σ时,分形流场和规则流场下游位置的〈w′〉1/2/〈v′〉1/2在0.8~1.2范围内波动.同时结合Hurst和Vassilicos[12]的研究结论可知,该脉动速度比值越接近1,说明此时流场的大尺度各向同性效果越好,并且反映出了流场在Y-Z方向上的对称性.
2.2 Q值瞬时等值面
为了进一步探讨两类流场在统计时间(0≤Ttrack≤100Tr)内拟序结构发展的异同,采用速度梯度张量第二不变量Q值来进行识别,具体结果如6和图7所示.其中速度梯度的张量Aij=∂ui/∂xj包括两部分,瞬时应变率张量sij=(∂ui/∂xj+∂uj/∂xi)/2和瞬时旋转率张量ωij=(∂ui/∂xj-∂uj/∂xi)/2,根据定义,速度梯度张量第二不变量Q=Qω+Qs=(ωijωij/2-sijsij/2).FGT选取的Q值瞬时等值面为Q/(1/Tr2)=4×10-4.根据之前的文章[26]研究可知,RGT的衰减速度要快于FGT,其涡度值也更低.为了在相同的统计时刻下清晰识别RGT的拟序结构,RGT选取的Q值瞬时等值面为-1×10-5.
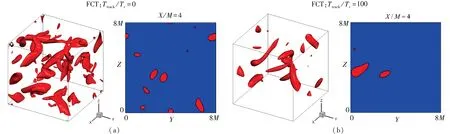
图6 FGT不同时刻下的Q值瞬时等值面
在图6和图7中,左图是流场拟序结构三维效果,右图为流向位置X=4M的平面上拟序结构二维效果.在图6的分形流场中,存在尺度大小不一的拟序结构,但明显以大尺度结构为主.而且大尺度结构的位置主要靠近边界区域,外形类似于经典的“虫子结构”[28,29].同时图6(a)和图6(b)的右图X=4M二维平面上的拟序结构也可以看出,此过程中大尺度结构普遍在流场边界区域运动,这与图3流向平均速度演化观察到的现象一致.
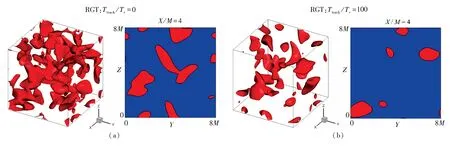
图7 RGT不同时刻下的Q值瞬时等值面
根据图7(a)和图7(b)的规则流场三维拟序结构发现,规则流场在此演化过程中不仅涡度值更小,整体的拟序结构尺度大小并未表现出强烈的反差,反而是拟序结构的尺度相比于分形流场分布显得更加大小均匀.当流向位置X=4M时,该二维Y-Z平面上的大部分拟序结构大小基本相同,结合图4的Y-Z平面上流向平均速度可视化结果,说明此时的规则流场演化至一种更加均匀的状态.
3 计算结果与分析
本研究将采用Yeung和Pope[30]提出的13点插值方法来获取粒子统计单元的拉格朗日数据,该方法也被称为TS13插值方案,并且其有效性也得到了Yeung和Pope[31]的证明.数值模拟时间步长为Δt/Tr=0.005,在课题组前期文章[26]的流场基础上,选取20 000个时间步长Δt/Tr,即统计时间段为0≤Ttrack≤100Tr.然后对流场中的流体粒子进行随机标记,追踪粒子的运动轨迹,从而探索粒子的运动规律.需要再次强调的是,此时的统计初始时刻Ttrack/Tr=0并非图2所示的流场演化初始时刻T/Tr=0,而是流场演化至一定状态后,选取其中的某一个时间段进行粒子追踪统计.
3.1 示踪粒子取样间隔的无关性验证
在Yeung和Pope[31]对TS13插值方法的应用中解释道,需要对示踪粒子在每一个时间步长下的具体位置和速度进行插值计算.由于采用DNS仿真,时间步长为Δt=0.005Tr,本研究在0≤Ttrack≤100Tr输出的数据大约将占用82 TB字节内存,这显然过于庞大,并且会严重延缓计算速度.根据2.1和2.2小节的结果可知,FGT和RGT两者的流场在0≤Ttrack≤100Tr内发展至近似均匀状态,因此将示踪粒子的取样间隔设置为Δt1=0.05Tr,即每10个时间步长进行一次统计.为了验证取样间隔对跟踪粒子计算结果产生的影响,分别对取样间隔为0.005Tr和0.05Tr进行初步试算,总计试算100个时间步长.在对示踪粒子轨迹的描述中,主要统计粒子沿流向X、法向Y和展向Z运动的平均位移〈X+〉i/M、〈Y+〉i/M和〈Z+〉i/M以及路程〈SX〉i/M、〈SY〉i/M和〈SZ〉i/M.其中符号“〈⋅〉i”表示对i个粒子进行整体平均.
当Ttrack/Tr=0的初始时刻,在分形流场和规则流场中随机标记Np=104个流体粒子.图8和图9分别是试算周期内,FGT和RGT中示踪粒子沿流向、法向和展向运动的平均位移轨迹结果.可以看出分形流场中,〈X+〉i/M、〈Y+〉i/M和〈Z+〉i/M均在4附近波动,示踪粒子在不同取样间隔时,沿流向运动的最大误差为0.05%,沿法向和展向运动的最大误差为0.005%和0.002%.而图9的规则流场中,〈X+〉i/M、〈Y+〉i/M和〈Z+〉i/M同样在4附近波动,沿三个方向运动的最大误差分别是0.04%、0.004%和0.002%.由此可见,释放104个示踪粒子能够充分采集到流场的拉格朗日信息,此时粒子运动采取不同取样间隔产生的最大误差仅为0.05%,这完全可以忽略.并且随着时间演化,流场将变得更加的各向均匀同性,两者之间的误差会逐渐减小.这说明在统计时间0≤Ttrack≤100Tr内,示踪粒子取样间隔产生的影响可以忽略不计.因此,后文统一将取样间隔设置为0.05Tr进行计算.

图8 FGT中不同取样间隔计算的示踪粒子运动轨迹
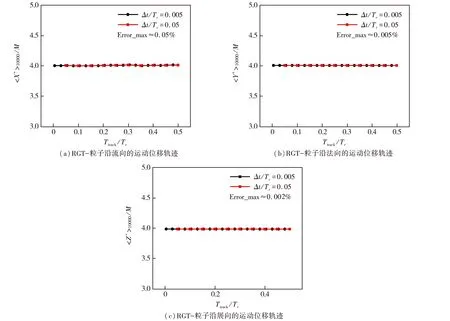
图9 RGT中不同取样间隔计算的示踪粒子运动轨迹
3.2 粒子数量对扩散规律的影响
由于3.1小节证明了示踪粒子取样间隔对粒子扩散无影响,本小节首先将在流场内随机标记Np=100、1 000、10 000个流体粒子,从Ttrack/Tr=0开始追踪粒子的运动轨迹,直到Ttrack/Tr=100统计结束.为了让读者对示踪粒子在流场中的分布情况产生直观的认识,当Ttrack/Tr=0,在流场范围0≤X,Y,Z≤8M内随机标记104个流体粒子,具体效果如图10所示,其中红色线条表示粒子初始释放范围的轮廓.此外,根据不同示踪粒子数量进行平均处理后,可以观察统计粒子的数量对流体微元扩散规律的影响.
图10 Ttrack=0时,104个示踪粒子在全流场中的分布情况
图11展示了在分形流场和规则流场中标记不同数量粒子后,示踪粒子沿流场流向运动的平均位移轨迹变化结果.可以看出,无论是分形流场还是规则流场,示踪粒子沿流向运动位移〈X+〉i/M始终在4附近成周期性波动.尤其是Np=100时,粒子在0≤Ttrack≤100Tr内一共运动了约4.5个周期.由于前文分析可知,该时间段内,流场流向平均速度满足〈U〉x/U0≈0.36,流向计算域长度为LX=8M,经计算发现粒子沿流向应该运动约4.5个周期,这与图11的结果一致.同时值得注意的是,标记的粒子数量越少,流体粒子更容易受到流场局部大尺度的影响,结合流场设置的周期性边界条件可知,粒子沿着流向运动平均位移将呈现出明显的周期性波动.然而随着示踪粒子数量增加,可以反映出对流场整体的系综平均效果.同时结合系统的质量守恒原则,当统计全流场中足够多的示踪粒子运动时,流体粒子沿流向平均运动位移值可以进行理论预测,即〈X+〉10 000/M=4,粒子沿流向运动平均位移波动幅度越小.这说明随着统计流体粒子数量越多,越能够充分反应出流场的真实情况.因此,当示踪粒子数量Np=104时,已经能够准确捕捉粒子的运动轨迹,证明粒子数量此时将不再影响粒子整体的扩散效果.

图11 不同数量的示踪粒子沿流向运动位移轨迹
3.3 分形结构对扩散规律的影响
由于课题组前期文章[26]中主要研究了分形流场的统计特性和能量耗散规律,因此本研究在此基础上进一步探索分形流场的输运特性.为了观察分形结构对流体粒子运动规律的影响,本节将在分形流场两个不同的区域(Run1:中心区域和Run2:对角区域)随机标记流体粒子,从Ttrack/Tr=0开始追踪粒子的运动轨迹.与此同时,为了进行对比,同样将在规则流场的对应区域标记示踪粒子,观察规则流场中粒子扩散规律与分形流场的差异.Run1的具体详情为Ttrack/Tr=0时,被动示踪粒子数量Np=104,释放范围为0≤X≤8M,2M≤Y,Z≤6M.Run1指定的中心区域以第一阶网格产生的大尺度运动主导,且小尺度运动始终被大尺度包围在中心区域,该区域的运动特性最为特殊.另外,Run2的具体详情为:Ttrack/Tr=0时,被动示踪粒子数量Np=104,释放范围为0≤X≤8M,4M≤Y,Z≤8M.该对角区域主要是第二阶和第三阶网格尺度较为集中,且位置远离流场的中心区域,研究该区域可探索分形流场中心区域的大尺度是否会对对角区域的流体运动产生影响.Run1和Run2指定区域的网格特点可见图1所示的网格二维几何结构,接下来将分别对Run1和Run2的计算结果进行分析.
3.3.1 Run1中心区域的结果分析
当计算工况为Run1时,统计初始时刻,示踪粒子在流场中的分布情况如图12所示.其中的红色矩形并非真实存在,而是为了便于识别初始的粒子位置所标记.图13为Run1的示踪粒子在分形流场和规则流场中运动轨迹随时间变化效果.在前文已经提到,主要统计示踪粒子沿流场流向、法向和展向运动的平均位移和平均路程.
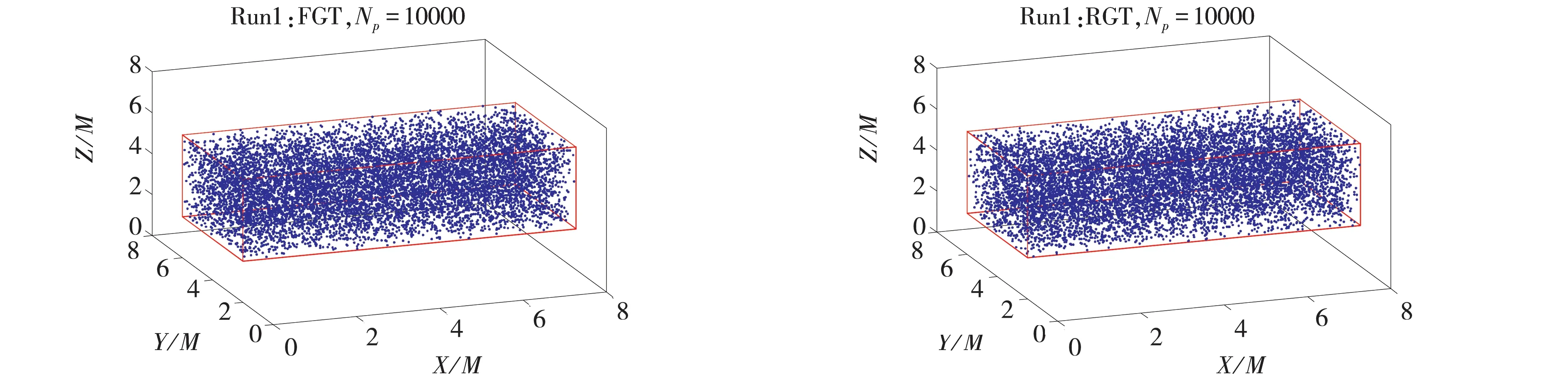
图12 Ttrack=0时,Run1的104个示踪粒子在流场中的分布情况
从图13(a)的示踪粒子沿流向运动的平均位移可知,无论是在分形流场或规则流场中,〈X+〉10 000/M始终在4附近波动,且波动幅度大致相同,说明两类流场中心区域沿流向上的湍流特性具有相似性.图13(b)为示踪粒子分别沿法/展向运动的平均位移轨迹,对比FGT和RGT发现,规则流场中的粒子沿法向或展向运动位移波动幅度较小,〈Y+〉i/M和〈Z+〉i/M几乎约等于4.而分形流场的粒子沿法向或展向运动时,〈Y+〉i/M和〈Z+〉i/M均呈现出远离4的趋势,说明分形流场中粒子沿法/展向扩散强度更大.对于图13(c)的粒子沿流向运动平均路程而言,FGT和RGT中的示踪粒子沿流向运动路程与统计时间成线性关系〈SX〉i≈0.36ΔTtrack,同时Ttrack=100Tr时,两者的路程均满足〈SX〉10 000/M≈36.值

图13 Run1的示踪粒子运动轨迹
得关注的是图13(d)的粒子沿法/展向运动平均路程变化结果,具体在FGT中,示踪粒子沿展向运动路程约为法向1.1倍,且当Ttrack=100Tr时,〈SY〉10 000和〈SZ〉10 000大约在0.5M~0.6M之间.而在RGT中,示踪粒子沿展向运动路程约为法向的1.2倍,且当Ttrack=100Tr时,〈SY〉10 000和〈SZ〉10 000大约在0.15M~0.2M之间.这说明,两类流场中的粒子沿展向运动能力都略强于沿法向运动,同时FGT流场的展向和法向各向同性效果更好,这一点从图5(b)的流场展向与法向脉动速度比值结果也可以得到证明.此外,FGT中粒子沿法/展向运动路程大约为RGT的3倍,意味着分形流场的示踪粒子沿法/展向的扩散强度比规则流场更大.
3.3.2 Run2对角区域的结果分析
当计算工况为Run2时,统计初始时刻,示踪粒子在流场中的分布情况如图14所示.图中的红色矩形框同样是为了便于识别初始的粒子位置所标记.分形流场的该区域以第二阶和第三阶网格尺度尾流运动为主,同时位于边界处的流体粒子沿法向或展向运动会不停地穿越边界,结果可与图12的结果进行对比.
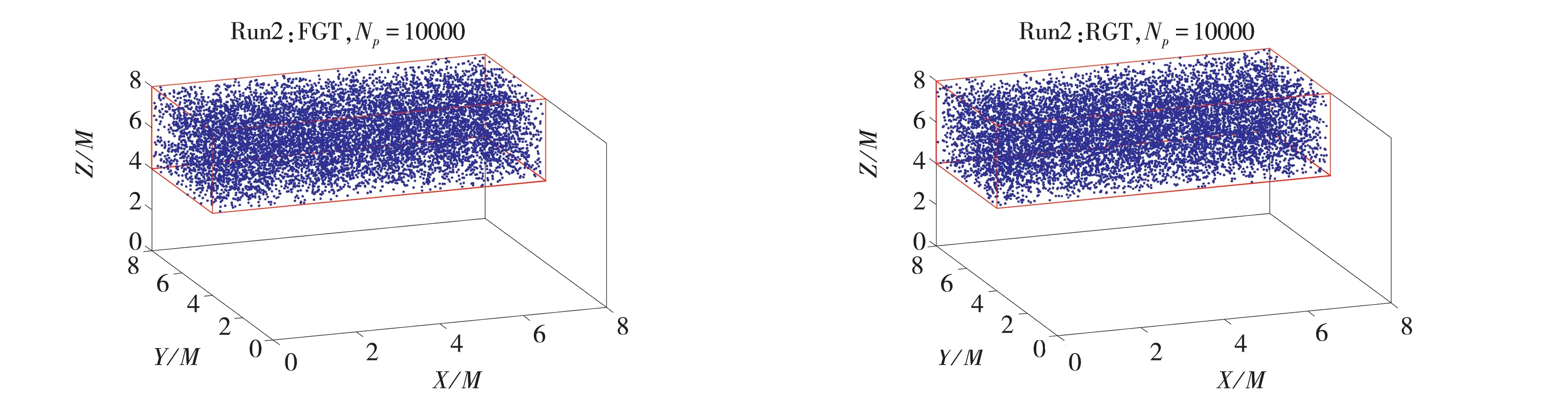
图14 Ttrack=0时,Run2的104个示踪粒子在流场中的分布情况

图15 Run2的示踪粒子运动轨迹
Run2工况的计算结果见图15.图15(a)与图13(a)一样,FGT和RGT中示踪粒子沿流向运动的平均位移始终在4M附近波动.其中示踪粒子沿流向运动平均位移出现波动且波动随时间增大的原因是:流场随着时间的演化,本应该聚集在中心区域和对角区域的流体微元将逐渐随机逃逸出指定区域(具体效果可见图16),这些逃逸出去的粒子则反映了流场的局部不均匀性.另外结合图3和图6的分析结果可知,分形流场在0≤Ttrack≤100Tr内,大尺度结构逐渐移动到流场的边界区域,这就导致了该区域流体粒子沿流向运动的扰动强度比Run1的中心区域更加剧烈.说明在该统计时间段内,分形流场依然受到局部大尺度运动的影响,所以图15(a)中FGT的结果曲线明显比RGT波动的幅度更大.不过可以确定的是,当FGT和RGT演化足够长的时间后,两类流场都将逐渐变成均匀各向同性湍流HIT(Homogeneous Isotropic Turbulence)状态.而在这个过程中,流场逐渐变得高度均匀,示踪粒子沿流向运动的平均位移波动也会逐渐减小,最终等于图11所示的理论值〈X+〉10 000/M=4.
图15(b)与图13(b)不同的是,无论是分形流场还是规则流场中的示踪粒子,其沿法/展向运动的平均位移从初始的6M位置处逐渐减小,意味着Run2对角区域的流体粒子在朝着流场的中心区域运动.但很明显的是,分形流场示踪粒子沿法/展向运动的平均位移幅度均大于规则流场.规则流场可能是因为中心区域特殊的湍流特性,导致了对角区域的流体粒子朝着中心区域运动.而在分形流场中,除了中心区域特殊的湍流特性外,可能还因为边界处的较小尺度尾流在运动过程中容易被卷入大尺度尾流中,受到大尺度运动的影响,导致了示踪粒子沿法/展向运动能力要比规则流场更强.图15(c)的粒子沿流向运动路程与图13(c)一致,不再赘述.图15(d)中,分形流场和规则流场的示踪粒子沿法/展向运动路程变化趋势与图13(d)几乎一样,分形流场的示踪粒子沿展向运动路程大约为法向的1.1倍,而规则流场的该值约为1.2倍.分形流场中示踪粒子沿法/展向运动路程同样约为规则流场的3倍.
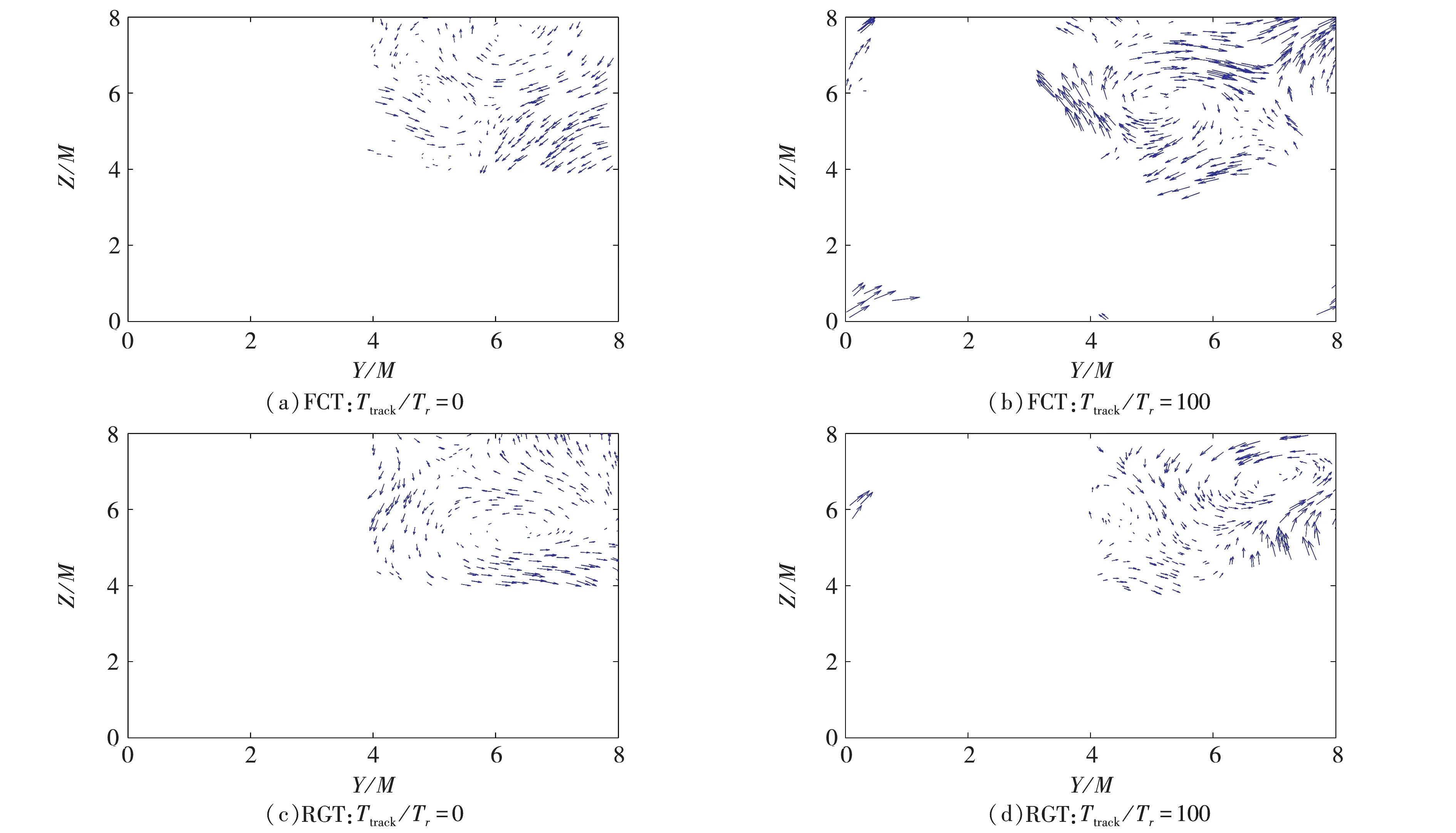
图16 不同统计时刻下,Run2的分形流场和规则流场中某Y-Z平面上示踪粒子矢量分布情况
图16表示不同统计时刻下,分形流场和规则流场中某Y-Z平面上流体微元运动的二维矢量图.其中Y-Z平面的定义为:当示踪粒子沿流向运动位移值在范围3.9M≤X+≤4.1M内,认为示踪粒子出现在该Y-Z平面上.统计时刻Ttrack=0时,对比图16(a)和图16(c),可以看出示踪粒子集中分布在对角区域,但分形流场中流体微元分布更为混乱.然而当统计时间为Ttrack=100Tr时,尽管图16(d)的规则流场中示踪粒子分布展现出一定程度上的混乱,但沿法/展向运动还是主要集中在范围4M≤Y+,Z+≤8M内.而此时图16(b)的分形流场中,示踪粒子沿法/展向运动明显更加混乱,其中在范围4M≤Y+,Z+≤8M内示踪粒子运动出现了明显的漩涡状,该位置正好对应中心区域的第一阶大尺度分形结构.同时可以看出,分形流场有大量示踪粒子逃逸出对角区域朝着中心区域运动,结合图15(b)的分析可知,分形流场中心区域特殊的湍流特性会对对角区域的流体微元运动产生影响,随着时间演化,边界上的小尺度尾流将逐渐被卷入大尺度尾流中,从而增大流场湍流混合度.
通过标记流场中足够数量的流体粒子后,对示踪粒子的运动轨迹进行统计发现,分形流场的对角区域主要集中为较小尺度运动,流体运动容易受到中心区域大尺度的影响,导致流体微元朝着中心区域运动的幅度更大.同时由于受到局部大尺度运动影响,分形流场湍流混合能力更强,示踪粒子沿法/展向扩散的程度及范围都比规则流场更大.此外,也说明分形结构能增强流场的横向湍流混合扩散强度,可以基于此原理,利用分形结构设计,开发合理的工业元件,以实现对流动的被动控制.
4 结 论
本文针对具有相同阻塞率的FGT和RGT,当流场演化随时间至近似均匀状态后,通过在两类流场的不同区域释放被动标记的流体粒子,对示踪粒子的运动规律进行统计,具体分为两种工况Run1和Run2.主要结论如下:
(1)当示踪粒子初始在某方向的释放范围为[0,8M]或[2M,6M]时,其粒子沿该方向运动的平均位移值将等于理论值〈X+〉10 000/M=4.另外,示踪粒子沿流向运动平均路程与统计时间同样满足理论计算的线性关系〈SX〉i≈0.36ΔTtrack.
(2)工况Run1表明,在中心区域两类流场的示踪粒子沿法/展向运动的平均位移均在4M附近波动,但分形流场的局部不均匀性导致波动幅度要略大于规则流场.此外,示踪粒子沿法/展向运动的平均路程大约是规则流场的3倍.
(3)工况Run2表明,分形流场的对角区域存在大尺度运动,导致示踪粒子沿流向运动位移的波动幅度要大于规则流场.同时在两类流场中,对角区域的示踪粒子沿法/展向均朝着中心区域运动,但分形流场的粒子运动范围更大.由于分形流场依然受到大尺度运动的影响,使得示踪粒子沿法/展向运动的平均路程同样满足规则流场的3倍关系.

