基于BP 神经网络的船舶气象航线决策系统

张大恒，张英俊，张闯

1 大连海事大学 航海学院，辽宁 大连 116026

2 大连海洋大学 航海与船舶工程学院，辽宁 大连 116023

0 引 言

为了实现船舶交通安全、经济运营，降低燃油消耗量，需要通过航线优化来确定船舶航线。船舶最优航线对于远洋捕捞、海上救援、溢油以及沿海灾害（如海啸和台风）中紧急疏散等至关重要。然而，船舶航线受海洋和大气环境的影响非常显著，Prpić-Oršić等[1]提出，在恶劣气象条件下航行可使船舶燃油消耗量增加50%以上；逆流等会降低船舶的相对速度并增加燃油消耗量[2]。因此，在航行过程中，考虑了周围海洋和大气条件的船舶最优航线对于船舶航行非常重要。船舶气象航线是考虑指定航程的天气和海洋条件、船舶特性、领海等诸多因素[3-4]确定的最优航线，基于实际运行数据的研究表明，船舶采用气象航线后，燃油消耗量可降低3%[5]。

船舶气象航线是最短航线[6]、安全航线[7]和最低燃油航线[8]的组合和优化[9]。以往的研究都试图寻求计算量最小化。如Journée 等[10]提出的等时线法是寻找船舶气象航线最优路径的常用方法，但它必须先验地手动确定。Hagiwara[11]利用自动等时线检测算法对其进行改进，使之适用于计算机处理；然而，自动等时线法经常会产生“等时线环”，导致无法找到航线，并且它也无法避免航线穿越陆地。因此，很多学者致力于采用动态规划方法，设计船舶气象航线决策系统网格尺寸，以减少工作负荷[12-13]。Zaccone 等[14]提出了一种三维的多阶段动态规划方法，船舶的航向和航速通过气象预报图获得。Bentin 等[15]在散货船上使用A*算法，同时通过风力辅助推进，实现燃油消耗量优化。Vettor 等[16]使用遗传算法，在2 个港口之间以船舶燃油消耗量和到达时间为船舶风险条件，在每条航线上寻找帕累托最优(Pareto optimality)路径和航速。上述方法的主要缺点是路径规划期间需要分析船舶运动模型，导致规划的航线精度低、节点数量多、存储空间大、灵活性差、计算速度慢。

人工神经网络可用于复杂系统建模，它具有极强的适应性、鲁棒性、容错性和表面拟合能力，非常适用于预测分析。Beşikçi 等[17]比较了采用人工神经网络（ANN）和多元回归（MR）模型在不同操作条件下对船舶燃油消耗量的预测结果；与MR 模型相比，ANN 模型具有更高精度，结合气象航线系统可为用户提供优化的航行参数，以减少燃油消耗量和环境影响。

在充分考虑船舶特性和航行特点的基础上，本文拟采用BP 神经网络方法，统计和分析船舶燃油消耗模型，为船舶气象航线决策系统提供数据支持；提出基于BP 神经网络燃油消耗预测模型的船舶气象航线决策系统；通过12 335 t 多用途船营口至仁川航线的仿真分析，获得船舶气象航线，验证基于BP 神经网络的船舶气象航线决策系统方法的可行性和有效性。

1 船舶燃油消耗预测模型

1.1 数据预处理

为了开发基于BP 神经网络燃油消耗预测模型的船舶气象航线决策系统，需要大量的训练和测试数据，才能准确预测各种操作因素下的船舶燃油消耗量。

船舶航行期间，船员每4 h 记录1 次航海日志和轮机日志，每24 h 提供1 次午报，包括船舶每日的燃油消耗量以及各种参数的平均值，例如吃水、航速、航行时间、航行距离、船位、目的港、气象条件、主机和辅机燃油消耗量以及所用燃油的类型。船舶运行数据是船舶在各种气象条件和不同航行速度下评估燃油消耗量的主要指标。本文用于仿真实验的12 335 t 多用途船，通过分析其自2018 年3 月开始共计656 d 的船舶运行数据，得到该船航行时间占比62.5%，在港时间占比37.5%；每个航次平均在港时间14.7 h，平均航行时间24.5 h。该船配备了2 台主机，其主要参数如表1 所示。

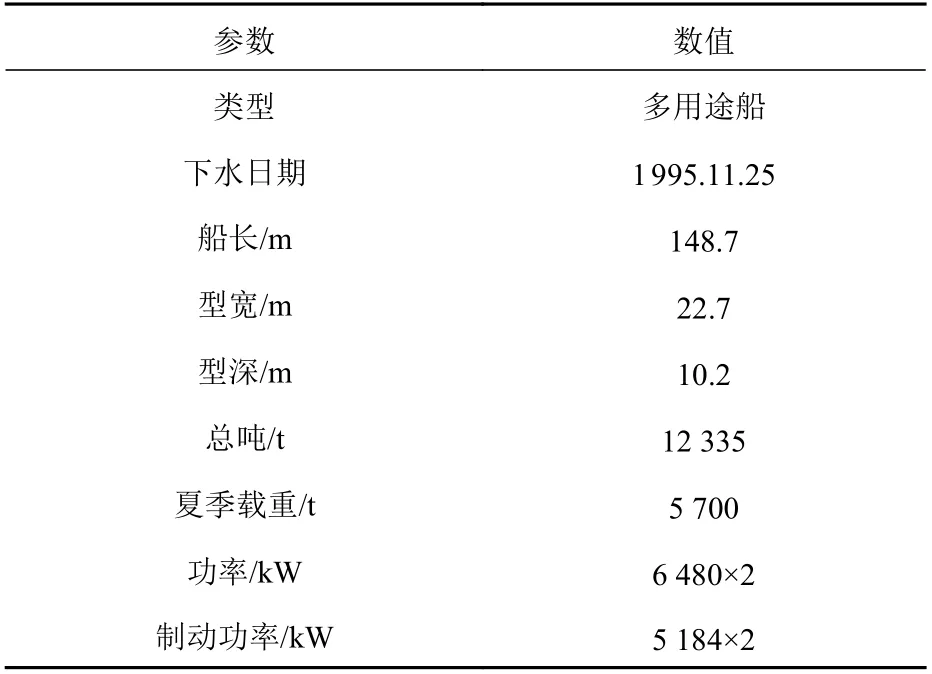
表1 船舶参数Table 1 Ship parameters

燃油消耗预测模型共有7 个输入参数：船速、主机转速、平均吃水、吃水差、船上货物重量、风和海浪的影响。采用黑箱模型[18]对船舶燃油消耗量进行建模。

由于7 个输入变量的单位不同，其幅度差异较大，直接将原始数据输入神经网络进行训练会降低算法的性能和收敛性。因此， 本文采用z 分数标准化方法对数据进行标准化处理：

式中：x*为标准化数据；u为样本数据的均值；σ 为样本数据的标准差。

1.2 BP 神经网络

Gkerekos 等[19]研究发现采用额外树回归（ETR）、随机森林回归（RFR）、支持向量机（SVR）和人工神经网络（ANN）对燃油消耗量建模时，可获得最佳性能结果；然而只有人工神经网络和支持向量机这种参数建模方法，可减少训练数据和计算成本，更适合分析气象航线。与支持向量机相比，人工神经网络在气象航线的实时性和准确性方面的效果更优。

BP 神经网络是一种基于误差反向传播的多层前馈人工神经网络，它能以任意精度逼近任意非线性映射，并能学习和适应位置信息，还具有用于数据存储和处理的分布式结构。神经网络具有较好的容错性、学习性和鲁棒性。其中，层数量用于控制神经网络的深度，而通过每层节点数量控制其宽度。增加一层的宽度可以提高它的记忆能力，而增加网络的深度可以提高它在不同层上学习特征的能力。但若层数及节点数量过多，会导致模型过度拟合[20]。实验结果表明，神经网络对复杂问题具有自适应能力。在完成前向传播后，可获得实际输出值的误差，然后用反向传播算法得到各层的输出误差，并对各神经元的连接权值进行校正。当神经网络输出层的误差平方和小于规定的误差时，完成训练并保存网络的权值和偏差。

传统神经网络中最常用的激活函数是Sigmoid函数，Sigmoid 函数是神经网络的核心。从数学角度看，非线性Sigmoid 函数对中心区域信号的增益较大，两侧信号的增益较小，对信号特征空间的映射有非常好的效果。利用加权输入的非线性组合产生非线性决策边界。从神经科学的角度来看，中枢区域类似于神经元的兴奋状态。两侧区域类似于神经元的抑制状态。因此，在神经网络训练中，关键特征在中心区域，非关键特征移到两侧。

近年来Relu 函数在神经网络中得到了广泛的应用。与Sigmoid 函数相比，Relu 函数具有计算简单、导数简单、收敛速度快、单边抑制和较宽的边界等优点。但是网络在训练过程中非常脆弱，一旦其输入值为负，很容易使神经元的值为0，导致训练停止。因此，在Relu 函数的负半区间引入Leaky 值，所以称为Leaky Relu 函数。本文采用Leaky Relu 函数作为激活函数。使用Leaky Relu 的好处就是：在反向传播过程中，当激活函数输入小于零的时候，也可以得到梯度（而不是像Relu 函数一样值为0），这样就避免了梯度方向的锯齿问题。

1.3 船舶燃油消耗预测模型结构

船舶燃油消耗预测模型的数据集取自该船656 d 的航海日志、轮机日志、油类记录薄和午报，共计3 936 份数据。随机抽取3 150 份（80%）数据样本作为训练集，其余786 份（20%）数据样本作为验证集。其中，输入变量有7 个，输出变量只有船舶燃油消耗量（单位：t/h），详见表2，表中的“风影响”和“海浪影响”分别为风速和浪高乘以影响因子得到的结果。

表2 BP 神经网络输入和输出变量范围Table 2 The range of input and output variables of the BP neural network

在BP 神经网络中，隐含层数的确定是一个非常重要和复杂的问题。如果隐含层数太少，则BP 神经网络的性能会很差或无法训练，并且可能无法生成足够数量的连接权值来满足BP 神经网络对样本的学习。如果隐含层数过多，虽然可以减小BP 神经网络的系统误差，但同时也增加了BP 神经网络的训练时间，容易陷入局部极小值而达不到最佳效果。

在确定隐含层数时，本文参考了文献[20]中的经验公式：

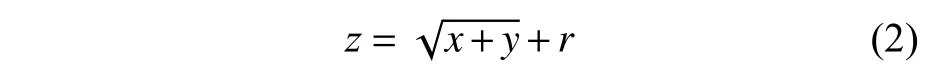
式中：z为隐含层数；x为输入层节点数；y为输出层节点数；r为[1,10]的常数。

在BP 神经网络模型中，隐含层数可通过实验获得。本文设计的BP 神经网络模型有7 个输入节点和1 个输出节点。经过多次实验可以发现，当隐含层数z=10 时，BP 神经网络的性能最好，训练次数（epochs）设置为10 000，BP 神经网络模型如图1 所示。

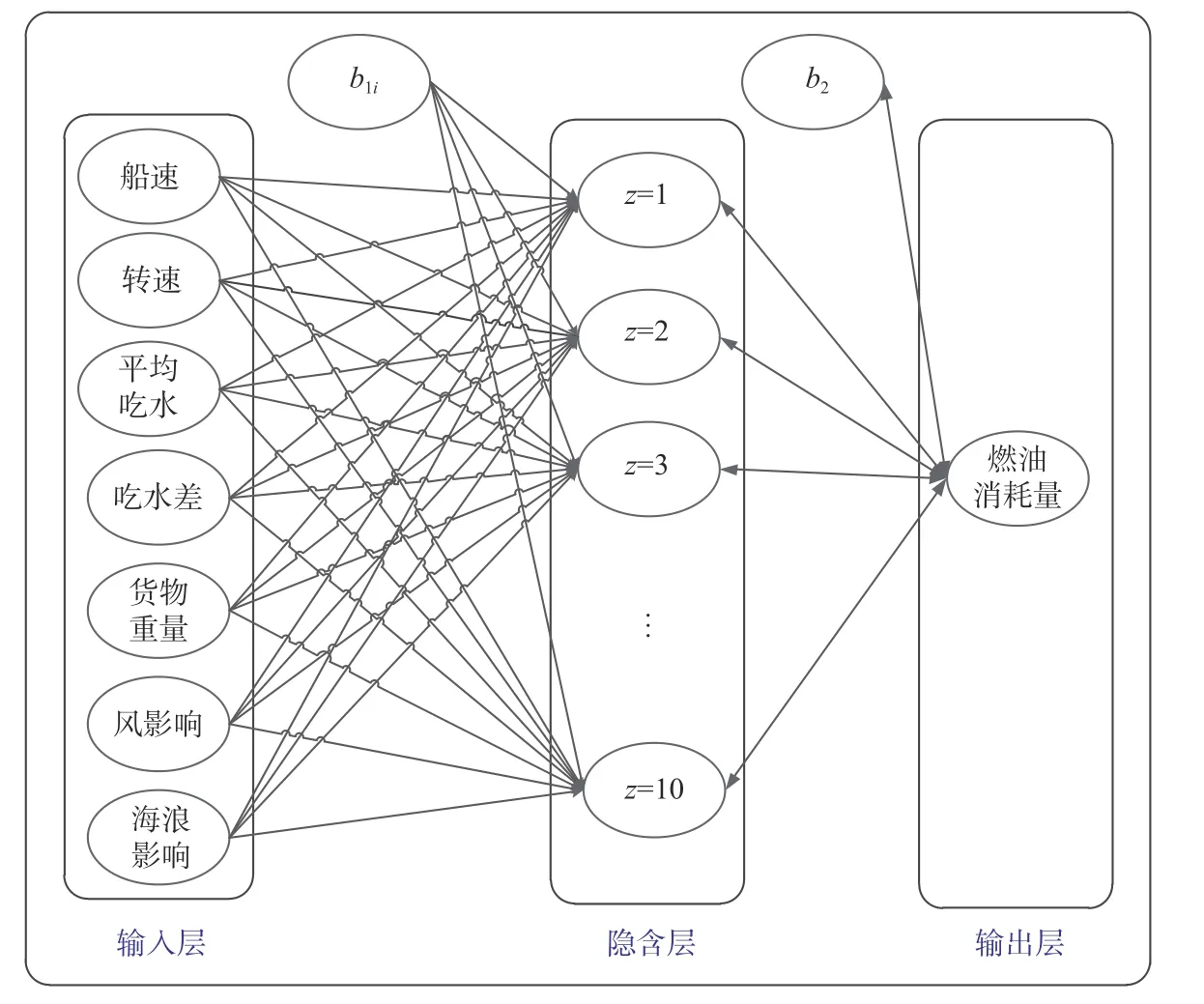
图1 BP 神经网络结构Fig. 1 BP neural network structure

本文的传递函数公式为

式中：ai=0.01，i取决于训练数据；xi与输入参数有关，公式为

式中：vship为船舶速度；R为船舶的主机转速；t为船舶吃水差；d为船舶平均吃水；G为船舶货物总重量；W为风对船的影响；S为海浪对船的影响；c1i～c7i和b1i分别为输入变量预处理权重和偏值。

利用训练好的BP 神经网络模型，可以求出实际的燃油消耗量：

其中，Ui公式为

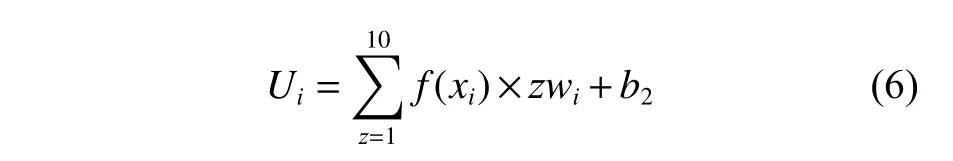
式中，wi和b2分别为BP 神经网络训练权重和偏值。经训练的权重和偏值如表3 所示。

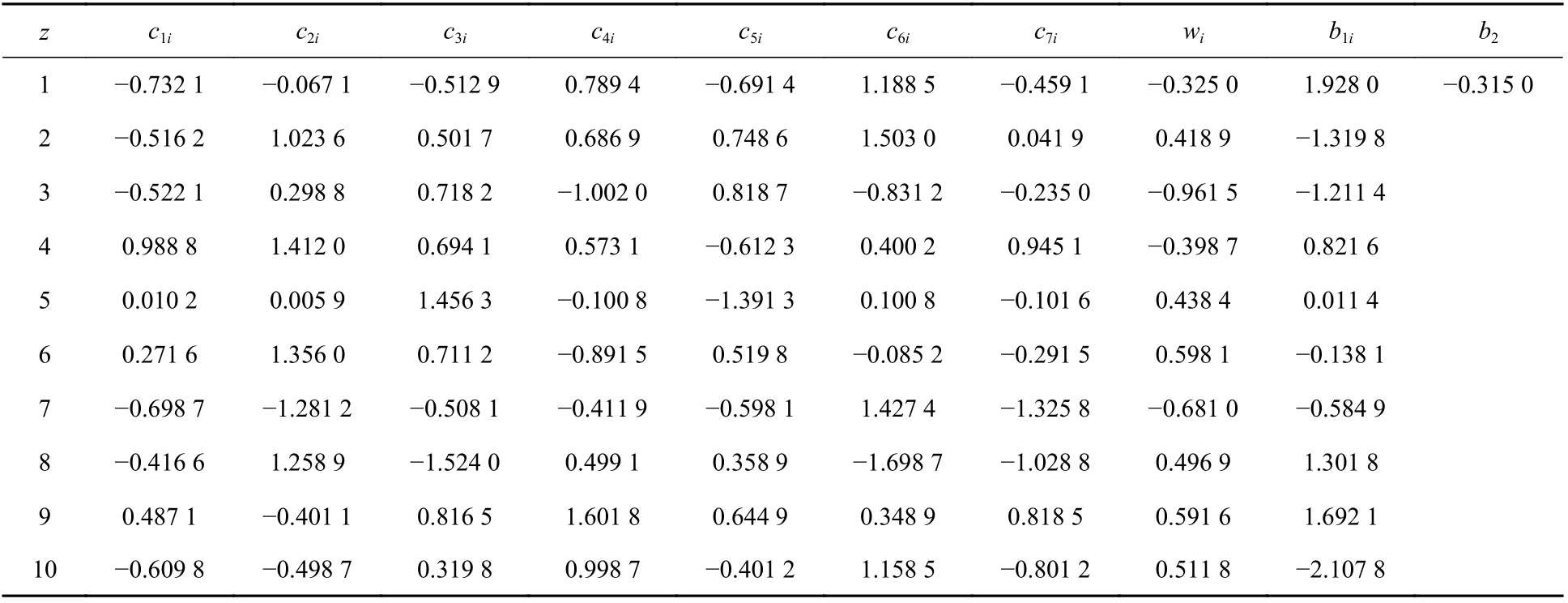
表3 输入层和隐藏层的权重和偏值Table 3 Weights and biases of the input layer and hidden layer

2 船舶气象航线决策系统

2.1 改进的Dijkstra 算法

对于网格化的海域，图论中的Dijkstra 算法在船舶导航中非常实用。Dijkstra 算法从一个特定的节点开始向外扩展，计算加权图中任意2 个顶点之间的最短路径。由于该算法需要搜索出发地和目的地之间的所有节点，因此如果以精细的横向间距对海域进行网格划分，则计算量非常大。本文研究中，在通过历史AIS 轨迹数据挖掘获得的先验船舶航线的基础上，对Dijkstra 算法进行改进，并引入新的代价函数，与原Dijkstra 算法中定义的启发式函数相结合，用于响应船舶周围的海洋和气象条件的影响。利用本文提出的改进Dijkstra 算法，根据上文建立的船舶燃油消耗预测模型，计算船舶在不同节点的船舶燃油消耗量，不断更新代价函数，并求取最低燃油消耗量航线。

本文将节点定义为地理坐标，航段弧是节点之间可能经过的路径，航段弧的成本定义为船舶燃油消耗量。航线算法的主要流程如图2 所示。

图2 改进的Dijkstra 算法流程图Fig. 2 Flow chart of improved Dijkstra algorithm

利用改进的Dijkstra 算法求取船舶气象航线的步骤如下：

1） 利用历史AIS 轨迹数据获取经验航线并提取其船舶转向点TRi[22]，在TRi之间设置不同节点vi；

2） 连接所有船舶转向点TRi和节点vi，找出连接始发港和目的港的经验航线，此时不考虑路径的燃油消耗量；

3） 根据式5）计算最短路径上船舶的燃油消耗量，保留可选择的节点vopt，以产生具有最低燃油消耗量的路径；

4） 循环遍历vopt和vi并应用Dijkstra 算法，通过vopti和vi确定连接始发港和目的港的最优路径；

5） 计算最短路径上船舶的燃油消耗量，保留可选择的节点vopt。

6） 重复步骤 4）～5），直到vopt没有变化，流程结束。

2.2 船舶气象航线决策系统框架及设计

本文提出的船舶气象航线决策系统模型，包括船舶历史数据处理模块、船舶燃油消耗分析模块、船舶航行数据处理模块、船舶推荐航线模块、用户信息交互模块以及船舶气象航线系统（图3）。

图3 船舶气象航线决策系统模型Fig. 3 Model of meteorological shipping route decision-making system

1） 历史数据处理模块的功能是利用船舶历史运营数据，如午报、航海日志、轮机日志、油类记录薄和气象预报的历史数据等，通过数据预处理平台进行数字化和标准化处理，将预处理后的数据输入到船舶燃油消耗分析模块。

2） 船舶燃油消耗分析模块的功能是把数据预处理模块的7 个输入变量（船速、转速、平均吃水、吃水差、货物重量、风和海浪的影响）和1 个输出变量（船舶燃油消耗量），通过BP 神经网络，获得船舶燃油消耗模型，用于计算船舶燃油消耗量。

3） 船舶航行数据处理模块的功能是将船舶导航定位系统、船舶自动识别系统、电罗经、计程仪等设备获得的船舶实时数据以及计划航线所航海域的气象预报数据等，转换为满足船舶燃油消耗模型要求的7 个输入变量，通过船舶燃油消耗分析模块计算实时的船舶燃油消耗量。

4） 船舶推荐航线模块的功能是利用该航线所有船舶的历史AIS 轨迹数据，通过轨迹聚类获得航线的船舶转向区域，并利用最优转向区域匹配算法和基于简单循环单元（SRU）网络获得不同类型船舶的推荐航线[22]。

5） 用户信息交互模块的功能是船舶驾驶员可根据船舶航次需求，如预计到港时间（ETA）、风和海浪对船舶的影响，修改船速或航向等。同时将修改后的参数输入至船舶航行数据处理模块的数据处理单元，进行数据处理，再通过船舶燃油消耗分析模块重新计算船舶燃油消耗量。

6） 船舶气象航线系统采用改进的Dijkstra 算法，在船舶推荐航线的基础上，考虑最新的天气预报信息，求取不同节点之间的船舶燃油最低消耗量，获取船舶最优航线；同时，船舶驾驶员还可根据航次计划要求调整航速和转速或航向，并重新计算最低燃油消耗量和最优航线。

该船舶气象航线决策系统框架，可通过修改系统参数，扩展到其他类型船型和航线。

3 仿真实验和结果分析

3.1 船舶燃油消耗模型性能分析

采用本文研究得到的BP 神经网络预测结果与多元回归分析（MR）结果进行比较。研究中，拟合优度（R2）、均方根误差（RMSE）、均方误差（MSE）可用于衡量BP 神经网络的性能。如果R2数值高，或者MSE和RMSE数值低，则表明模型拟合效果好。针对单一输出的神经元网络，常用MSE和RMSE作为误差指标。

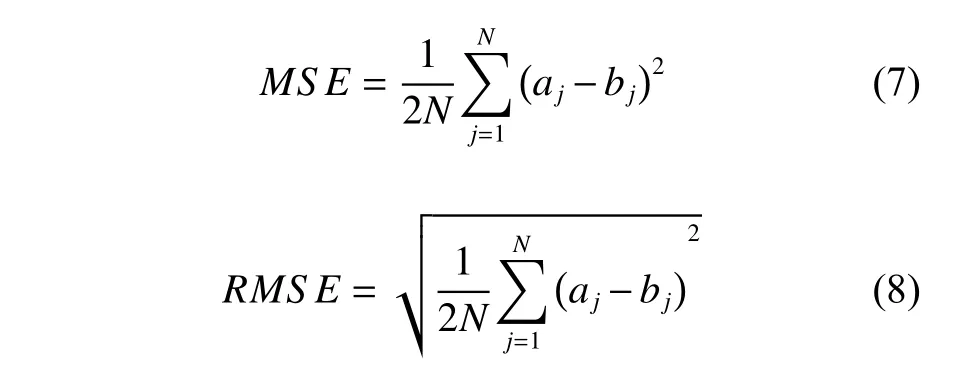
式中：N为训练总数；aj和bj分别为第j次训练的预测输出值和目标值。

如表4 所示，数据统计分析结果表明，该船的平均燃油消耗量为1.321 t/h。图4 是采用基于BP神经网络的船舶燃油消耗模型得到的预测值与实测值的比较分析结果，导出模型中R2=79.97%。其中，86.2%的预测点显示在其实际值的10%以内。偏差超过10%的数值，经分析，归因于在船舶航行海域观察到的实际气象条件与历史气象数据之间的差异。

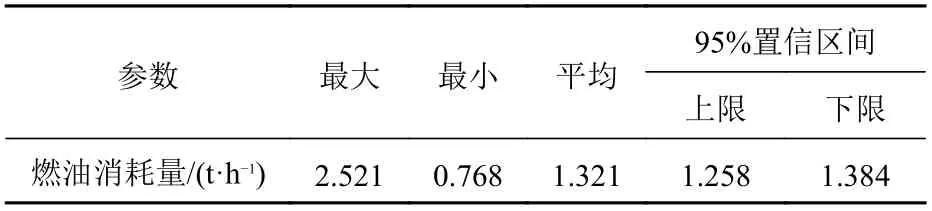
表4 燃油消耗量统计结果Table 4 Fuel consumption statistics results

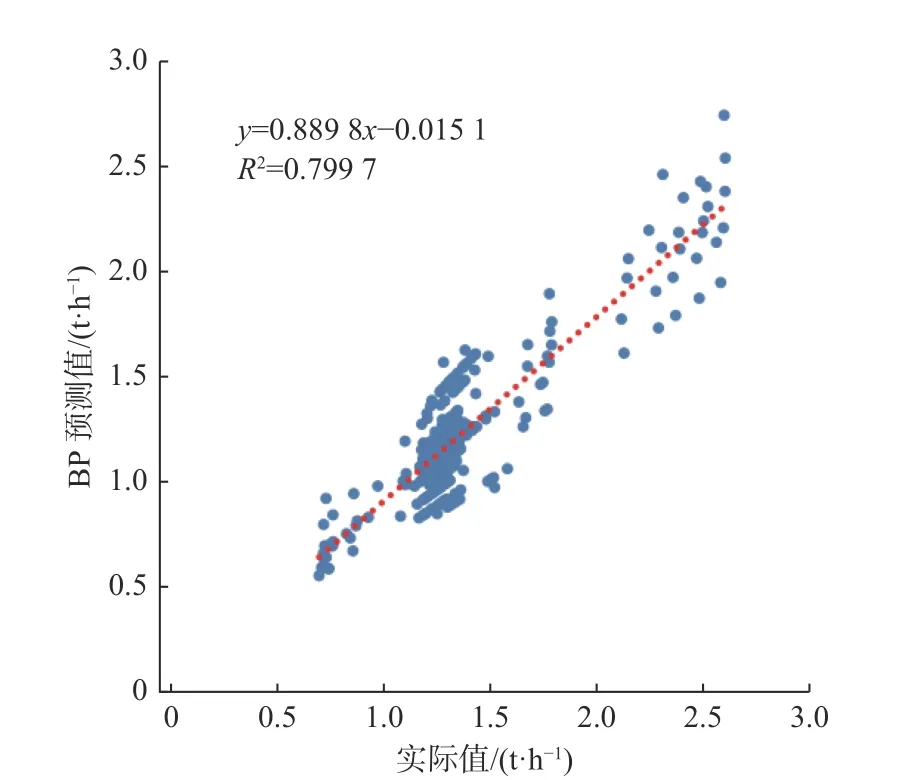
图4 燃油消耗实际值和BP 神经网络训练预测值对比结果Fig. 4 Comparison of fuel consumption predicted by BP neural network training and actual fuel consumption

为了更好地分析本文提出的基于BP 神经网络的燃油消耗预测模型的性能，采用多元回归分析（MR）模型与该模型进行比较。MR 是一种线性统计技术，其采用最小二乘法建立变量之间的最佳关系。本文用来预测燃油消耗量的多元回归分析模型为

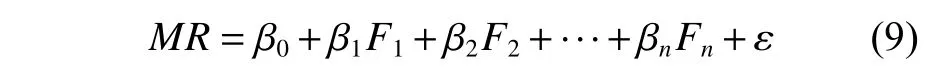
式中：β0，β1，···，βn为回归系数；F1，F2，···，Fn为自变量；ε 为模型误差。该模型具有线性形式，以表示变量之间的线性关系。

在性能分析时，多元回归分析模型采用与BP 神经网络训练相同的数据集，以便对两者进行比较。图5 所示为采用多元回归分析模型得到的预测值和实际船舶燃油消耗量，其中R2=72.68%，它表明多元回归分析可以拟合燃油消耗量。最终，得到验证数据的MSE和RMSE分别为0.032 0和0.178 9，如表5 所示。通过BP 神经网络模型与多元回归分析模型的比较，发现BP 神经网络模型的预测燃油消耗量的相关性远高于多元回归分析模型；此外，BP 神经网络模型对验证数据的RMSE远低于多元回归分析模型。

图5 燃油消耗量实际值和人工回归分析预测值对比结果Fig. 5 Comparison of fuel consumption predicted by MR analysis and actual fuel consumption

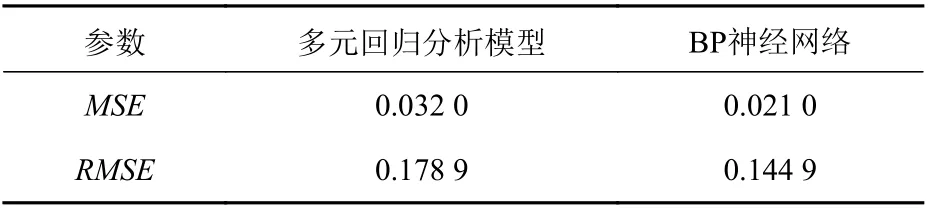
表5 BP 神经网络和多元回归分析模型得到的MSE 和RMSETable 5 MSE and RMSE of BP neural network and MR

3.2 船舶气象航线决策系统仿真实验

将基于改进Dijkstra 算法的船舶气象航线决策系统应用于多用途船从营口至仁川的航线。在仿真实验期间，海洋分析数据包含表2 中受风和海浪影响的603 个海洋位置的观测值，位置纬度和经度分辨率分别为0.01°和0.20°，如图6 所示，时间频率按航海日志的时间间隔，以4 h 为基准，中间点进行数据插值处理。实验的气象要素以船舶记录的历史数据和历史气象为基准，利用本文开发的船舶气象航线决策系统求取该船在不同航速情况下的最低燃油航线。

图6 环境模型Fig. 6 Model of the environment

图7 所示为不考虑气象要素和船舶燃油消耗量得到的船舶最短航线，从图中可以看出，该最短航线能够准确避开陆地及浅水环境，但其沿着海岸线，未经过老铁山水道，这些均与船舶实际航线严重不符，不利于船舶航行安全。

图7 不考虑气象要素和燃油消耗量的船舶最短航线Fig. 7 The shortest route of ships without considering meteorological factors and fuel consumption

图8 所示为利用营口至仁川航线的历史AIS数据提取的船舶推荐航线，图9 所示为考虑了气象要素和船舶燃油消耗模型，采用改进的Dijkstra算法获取的该航线某航次在不同航速下的船舶气象航线。从图中可以看出，船舶从营口港出发至大连海域附近的船舶航线基本没有大的变化，而推荐航线和气象航线的差异主要是受气象因素影响和船舶在不同气象条件下的船舶性能变化所致。因在山东半岛东北部海域存在西南风和海浪等不利于营口至仁川航线的气象条件，使得仿真得到的2 条船舶气象航线偏离山东半岛。由图9可见，船速为17 kn（黑色）和15 kn（绿色）的船舶航线也存在差异，其原因是在相同气象条件下（风向SW，风速20 kn，波浪向SW，浪高1.5 m），不同航速对船舶燃油消耗量的影响不同。燃油消耗量如表6 所示。通过分析船舶燃油消耗量可知，由于船舶航线中存在不利于船舶航行的气象条件，2 条航线的船舶平均燃油消耗量都高于表4的统计结果，但远低于最大燃油消耗量。仿真实验验证了利用船舶气象航线决策系统模型生成的气象航线既避开了不利气象要素，也保证了船舶航行安全，降低了燃油消耗量，且与该船在正常航行活动中的实际航线基本相符。

图8 基于历史AIS 数据的船舶推荐航线Fig. 8 Recommended shipping routes based on historical AIS data

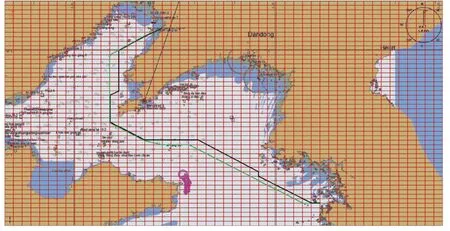
图9 改进的Dijkstra 算法得到的船舶气象航线Fig. 9 Ship meteorological route based on improved Dijkstra algorithm

表6 船舶燃油消耗量统计Table 6 Ship fuel consumption statistics

4 结 语

本文研究提出了基于BP 神经网络的船舶气象航线决策系统，它利用气象预报和船舶的燃油消耗预测模型，对AIS 数据挖掘的经验航线进行修正，以获得不同航速下的最低燃油航线。某多用途船营口至仁川航线的路径规划仿真结果表明，BP 神经网络能够非常准确地学习输入变量与船舶燃油消耗量之间的关系。与多元回归分析模型结果相比，BP 神经网络提供了相对更准确的船舶燃油消耗预测结果。该方法可用于评估船舶燃油消耗量和设计不同航速的最低燃油航线，以为船舶管理者提供决策参考。

考虑到不同船舶操纵性能的差异以及船舶燃油消耗量受海洋环境中不可控因素的影响，因此，未来可深入研究探讨如船舶稳性、能见度等其他输入变量与船舶燃油消耗量之间的关系。