基于逆优化的汽车配件服务网络服务能力优化

申国剑，张相斌，徐亚楠

（南京邮电大学 管理学院，江苏 南京 210003）

0 引言

中国作为世界上汽车保有量最大的国家，自2014 年起汽车保有量逐年增加。截止到2020 年底，全国的汽车保有量高达2.81 亿辆，相较于2014 年的1.54 亿辆，同比增长高达约55%，并且市场仍在不断扩大，这就使得汽车售后服务的重要性越来越显著。对于4S 店而言，提高售后服务能力、降低生产经营成本一直是其需要解决的主要问题，尤其是汽车配件服务，更是4S 店所需要解决的核心问题。汽车配件服务很大程度上取决于市场需求，汽车市场需求直接影响着配件的库存以及组装销售过程。目前，4S 店一直面临着因库存资源不足导致顾客满意度下降和顾客流失，或因配件库存过多导致经销商库存成本上升等问题。当零配件缺货时，若不能及时补货，往往会导致企业服务水平低下，造成客户流失，间接或直接影响企业利润；若配件库存积压严重，则会加大企业运营成本，资金周转率低下，不利于企业持续稳定地发展。早期4S 店的优化工作主要是以库存配件分类研究为主，常用ABC 配件分类法以控制库存。但随着配件种类越来越多，分类复杂程度越来越大，普通的分类方法已经无法满足企业决策需求，适用性大不如前。因此各学者在此基础之上针对方法的改进做了相关研究。刘晔、刘晓分析了ABC 分类方法的局限性，并在此基础之上提出了基于数据分析的多准则配件分类K-means 算法，进一步节约了企业的配件管理成本；Titty F提出一种新的模糊C 均值和机遇AHP 的三阶段方法，用于多准则ABC 库存分类，增强了方法的适用性和灵活性；Y Liu，Q Zhang为控制维修配件库存，结合天气条件进行了4S 店维修备件需求预测研究，预测模型显著优化了配件库存。随着优化需求的提高，近年来4S 店的优化方向逐渐侧重于营销策略、配件服务、需求预测、资源分配等角度。谢鹏寿、张宽等通过改进传统RFM（Regency，Frequency，Monetary）模型，构建了适用于新阶段4S 店顾客细分的TFM 模型，该模型更好地提高了4S 店管理效率，减少了顾客流失率；王玖河结合4S 店售后服务配件供应链管理的现状，构建CPFR 体系架构，提高了4S 店之间的协作性、共享性；范志强以交易费用、采购成本最小化，服务质量最大化为目标构建新的两级物流服务供应链多目标订单分配模型，提高了企业动态服务能力；刘念从动态演进角度切入，通过对多种案例进行分析，总结出服务创新能力升级的内在逻辑，为4S 店服务能力改进升级提供了重要思路；刘畅考虑到服务能力存在较为严重的不确定性，从服务能力的集成性、制约性角度出发，构建了供应商满意度与模糊能力的多目标、多阶段供应链调度优化模型和求解算法；Wang D构建了一个由两个SP 和一个SI 组成的服务供应链，并建立了五个分析模型，并得出“需求驱动的数据价值导致SI最优定价和SP 最优增值服务水平下降，影响需求驱动和供应驱动的数据价值”的重要结论。随着品牌4S 店企业的不断扩大发展，现阶段的4S 店为扩大市场，往往会选择在某个城市设立多个下级部门，为进一步优化，4S 店总部与下级部门需要形成两层关系即采用两级销售结构。即上级节点统一采购多种汽车配件，并将采购的配件分配给下层节点部门，下层节点再将配件进行组装加工成整车用以销售。然而在一定时期内，4S 店总部会因包括预算、加工水平等各方面因素，所能够得到的配件资源往往是有限的，无法满足下层所有部门的生产需求。为了充分使用现有资源，提高配件服务能力，获得最大经济收益，上层决策者则需要对有限资源进行合理分配，根据下级各部门所在市场需求情况，对购买的零部件实行错位分配，使得各部门零部件的库存水平保持差异性。

这种问题的优化复杂性较高、难度较大，两层规划方法可以较好地解决这类问题。两层规划的资源分配问题可以表述为：上级部门采购资源，并将有限的资源在下级各部门之间进行分配，使得自身与下级所属部门生产活动相关的目标达到最优或者满意；同时，下级部门根据上级分配的资源进行生产活动，使其收益最大化。两层规划起源于经济问题，中国学者夏洪胜、盛昭瀚等着力对Stackelberg 模型进行分析解释，并且在此基础之上考虑下层决策者关联问题，给出了优化算法，为以后的两层规划问题的研究奠定了基础。在分散供应链中的合作决策问题研究中，Haiyan Luo解决了预算约束作为企业范围供应链背景下有吸引力的特征的双层决策问题，但并未考虑不确定环境中的实际弹性需求和变量，为后续的研究提供了改进思路。

结合以往研究，学者在两层规划问题上往往将一段时间内企业拥有的资源作为刚性约束进行优化，忽略了在销售过程中企业与企业、部门与部门之间相互合作中资源约束为弹性的特点。逆优化方法则是研究企业在满足市场需求的前提下，通过横向补货来调整资源数量以降低需求不确定性带来的影响以及实现资源优化配置的方法。针对研究问题，本文在两层规划模型的基础上加入逆优化模型，针对下级节点部门的资源配置进行局部逆优化，从而在提高4S 店总体配件服务水平的前提下，减少企业运营成本。

1 汽车配件服务优化建模

4S 店作为一种以“四位一体”为核心的汽车经营模式，集整车、零配件、售后服务、信息反馈于一身。由于4S 店具有超高的针对性，每种4S 店只会经营单一品牌的汽车，这就使得4S 店需要进行统一组织、管理、销售。4S 店配件服务的经营模式大致如图1 所示：

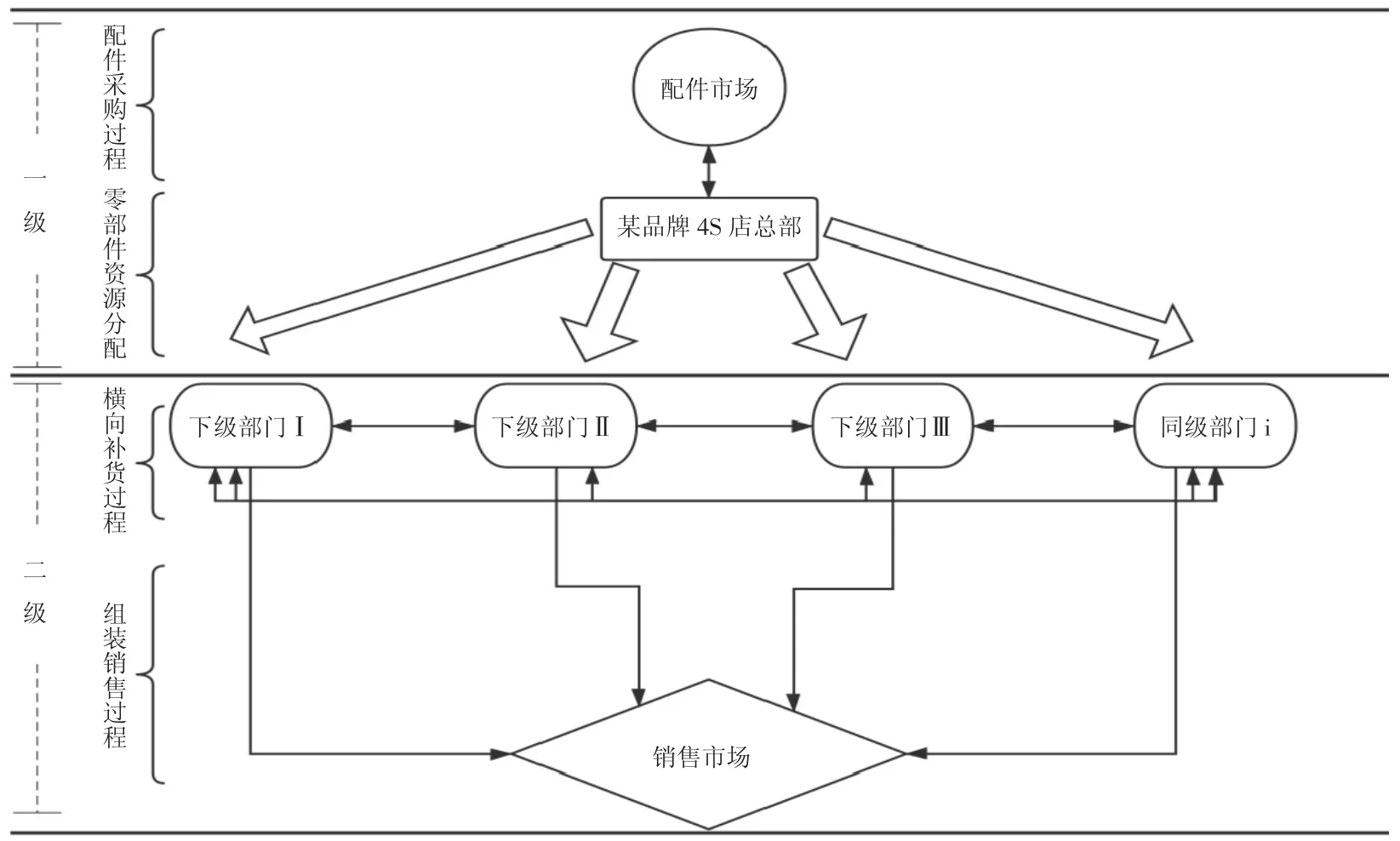
图1 某4S 店经营组织结构图

在该两级运行模式下，4S 店的上级、下级均有自己的目标。其中4S 店企业的下级生产销售部门以利润最大化作为主要目标，总部作为上级决策者，除了考虑利润最大化以外还需要考虑企业资源的使用情况，这就需要决策者可以纵观全局，通过决策使得整体最优。

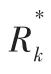
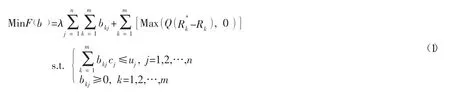
下层决策者需要将所分配到的资源组织生产，获得最大经济效益。其中p,k=1,2,…,m;i=1,2,…,l 表示第k 个部门生产第i种配件的经济价值，x，p,k=1,2,…,m;i=1,2,…,l 表示第k 个部门生产第i 种配件的数量，M,i=1,2,…,l;k=1,2,…m;j=1,2,…,n 表示第k 个部门生产第i 种配件所需第j 种零部件的数量，于是下级部门资源优化模型为：

于是，对于汽车配件服务网络服务能力优化的两层规划模型为：

该模型为一个上层决策者和多个下层决策者的非线性的两层单目标决策问题。由于上层分配的资源需要转化为整车产量，对上层决策者给定的每一个方案，下层决策者需要解决以求最大经济价值为目标的线性规划问题，因此对于下层决策者可使用一般线性规划算法进行求解。

2 局部资源配置逆优化建模

由于市场需求不是永恒不变的，在动态的市场需求环境下，下层各部门存在自有资源无法满足所有配件的市场需求或自有资源过分积压、难以销售的情况。随着科技水平的提高，ERP 系统、库存云与供销协同系统等一整套售后配件管理优化系统正在广泛应用于各企业部门，下级部门可以借助统一平台了解其他部门资源储备情况，及时向其他部门调用零部件资源，减少采购时间以及运输成本，即通过横向资源交易来提高自身的配件响应服务能力。在这个过程中，由于自身资源的限制，下级各部门均需要向其他部门调用零部件资源并同时调出自身富裕的相关资源。这就导致两层规划模型中的部分参数难以确定，因此需要引入逆优化方法对不确定参数进行调整，进而实现资源配置优化。

假设m 个下级部门在计划期内根据各自的需求生产l 种汽车配件，x,k=1,2,…,m;i=1,2,…,l 为m 个部门配件生产数量；p,k=1,2,…,m;i=1,2,…,l 为m 个部门汽车配件的边际价值；在提供配件服务过程中存在一部分资源能够满足配件服务的生产需求，一部分不能够满足，一部分则完全缺失；其中b,k=1,2,…,m;j=1,2,…,r 为m 个部门能够满足配件服务需求的自有资源；q,k=1,2,…,m;j=1,2,…,r 为m 个部门可以租出去的资源的市场价值；b,k=1,2,…,m;j=r+1,r+2,…,s 为m 个部门不能够满足配件服务需求的自有资源；q,k=1,2,…,m;j=r+1,r+2,…,s 为m 个部门需要租用的资源的市场价值；q,k=1,2,…,m;j=1,2,…,r 为m 个部门可以租出去的资源的市场价值；s,k=1,2,…,m;j=1,2,…,r 为m 个部门需交易用的资源的数量；b,k=1,2,…,m;j=s+1,s+2,…,l 为m 个部门缺失的资源数量；q,k=1,2,…,m;j=s+1,s+2,…,l 为m 个部门需要交易资源的市场价值；s,k=1,2,…,m;j=s+1,s+2,…,l 为m 个部门需要交易的市场资源的数量；M,k=1,2,…,m;i=1,2,…,l;j=1,2,…,n 为m 个部门生产单位第i 种汽车配件对第j 种资源的消耗量。Mx为m 个部门生产第i 种汽车配件对第j 种资源的总消耗量。

假设这m 个部门富余、缺失的零部件资源能够全部交易，则下级部门的优化目标是演变成根据上级部门给定的资源量组织生产并通过横向调节自有资源以及其他资源，来获得最大收益R，此时目标函数为：

将（4）式进行整理可得：

由于在配件服务过程中，部分自有资源能够满足市场需求，部分不能满足。本文取k=1，此时配件服务企业下级其中某一个部门的资源优化模型为：

对于下级各部门而言，市场需求直接决定了其生产数量。因此在资源交易的过程中，需要预先确定配件生产所需消耗的资源数量，使得生产量成为该资源优化模型的最优解。通过将自有资源量作为优化变量，用b 变化最小为优化目标，以式（6）的互补最优性条件为约束构建相应的逆优化模型。

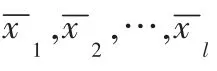
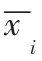
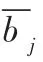
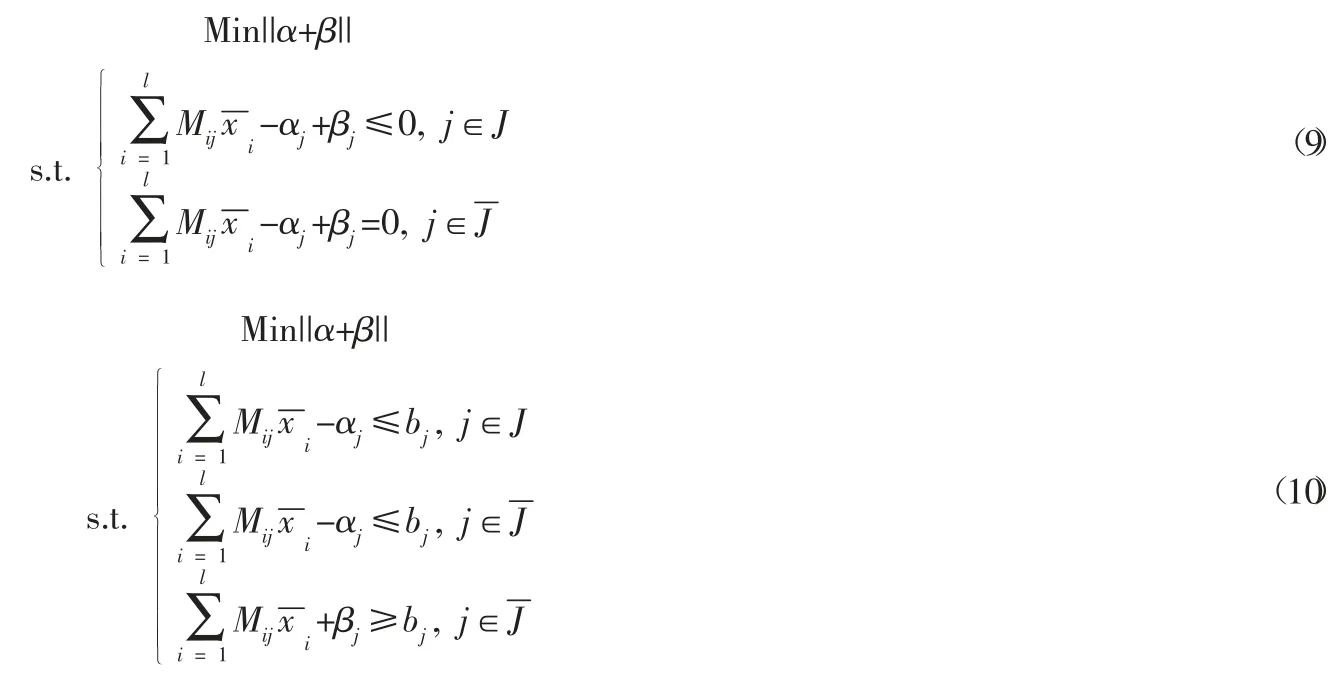
在选取范式l的情况下，整理式（10）可得：

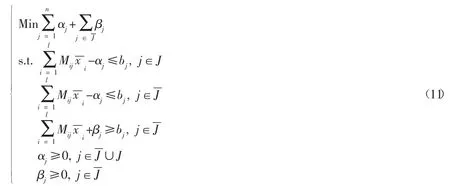
利用线性规划方法求解式（11）可得该部门所需的零部件自有资源为：

该部门可以租出的零部件资源h,j=1,2,…,r 可以表示为：

该部门需要向其他部门租进的零部件资源s,j=r+1,r+2,…,s,s+1,s+2,…,n 可以表示为：

3 算例分析

现如今，为扩大销售市场，提高企业利润，增强服务水平，各种品牌的4S 店在世界范围内旗下有多家下级门店。选取A市的某品牌4S 店，并以该4S 店为例。据调查，这种品牌的4S 店在该地区有3 个下级部门，分别为部门A、部门B 和部门C。并且三个部门分别生产三种相同型号的畅销汽车n、n、n，其中每种汽车在组织生产过程中均需要多种零部件用来组装成车，选取5 种核心配件r、r、r、r、r。以1 个季度为周期，为方便计算，将所得数据简化如表1 所示：

表1 资源使用情况

若上层决策者给定下层决策者的预定经济价值分别为950 万、800 万、700 万，取Q=1，λ=1×10，于是有：

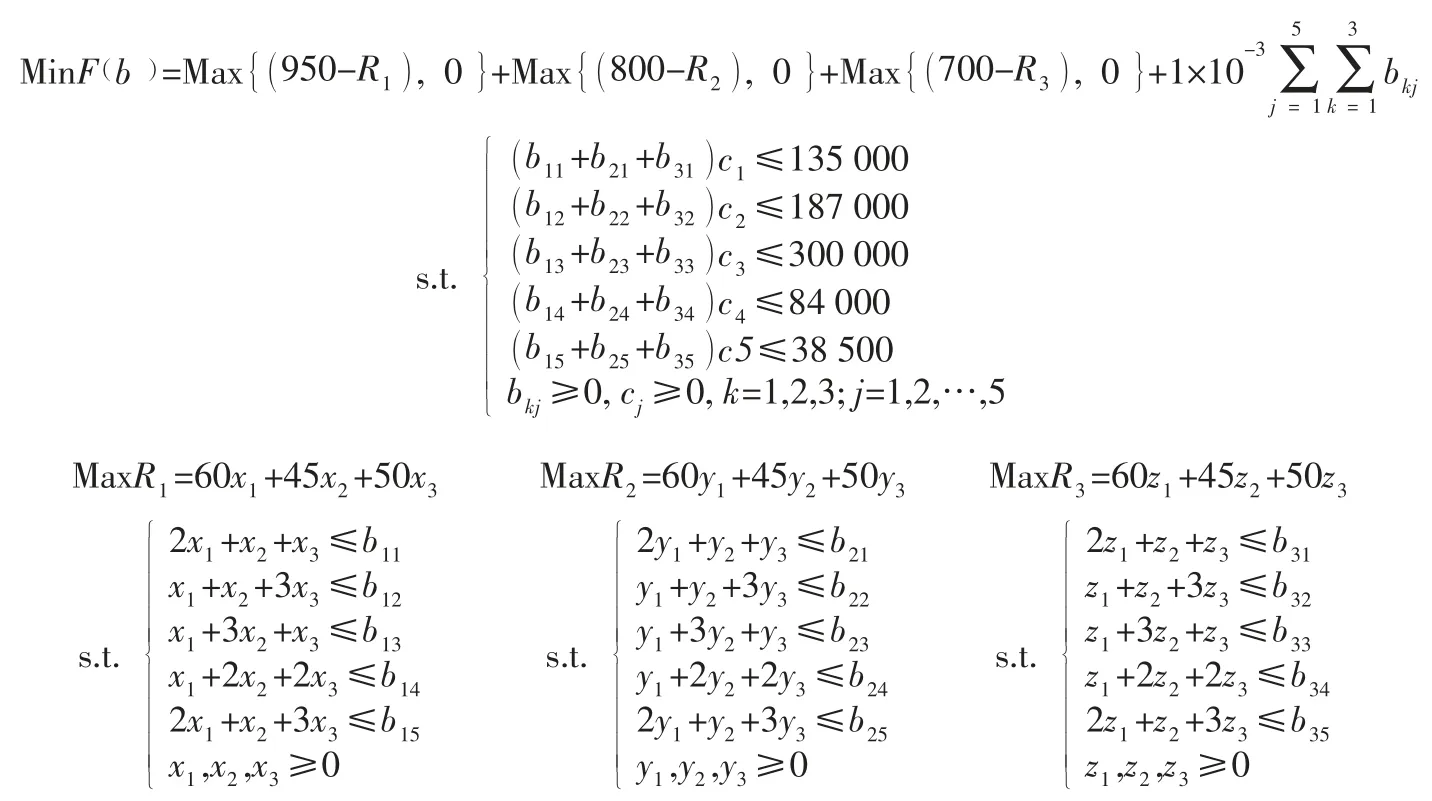
其中：x,x,x;y,y,y;z,z,z分别为第一个部门、第二个部门、第三个部门的三种车型生产数；R,R,R为三个子部门实际经济价值；b为第k 个部门分得第j 种零部件资源的数量。

采用改进智能粒子群算法，通过使用MATLABR2018a 进行求解，仿真迭代次数I 分别选取50、100、200、500，结果如图2 至图5 所示。

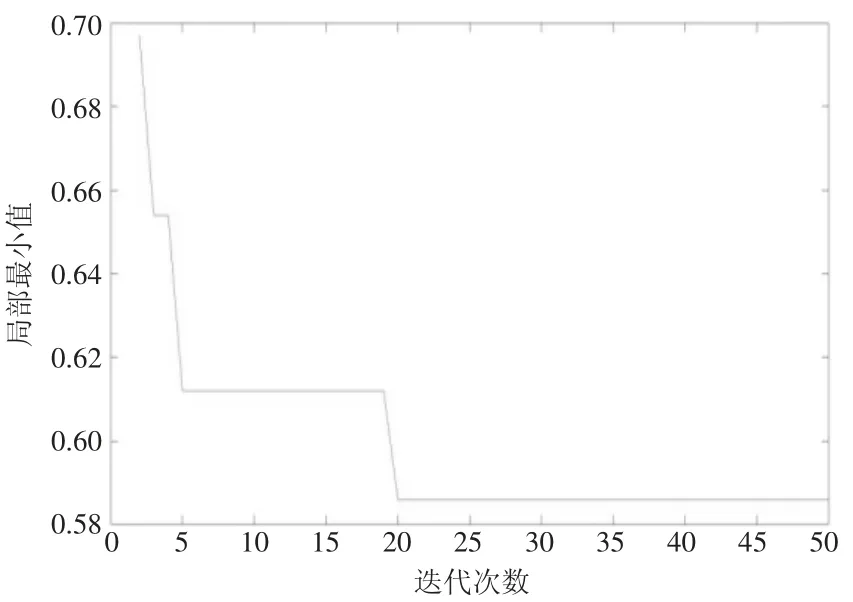
图2 I=50 时模型仿真结果

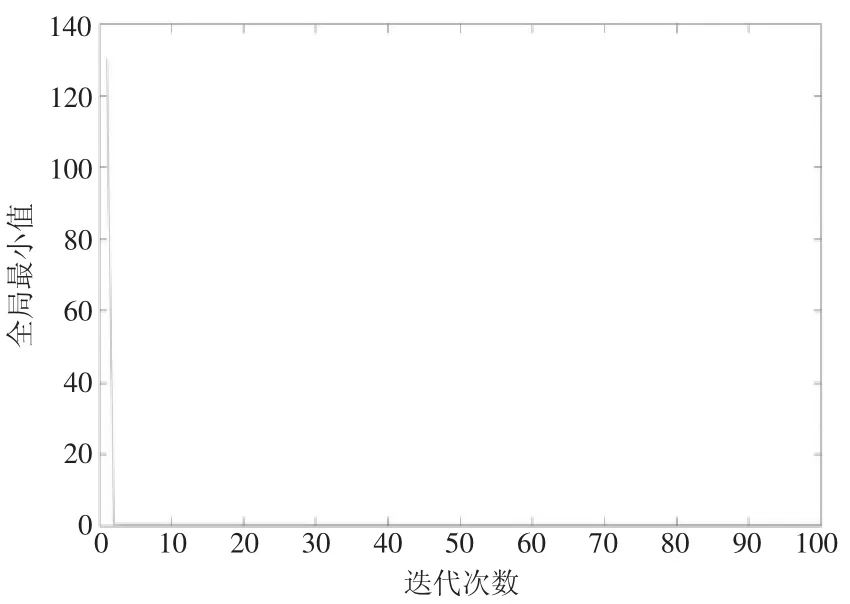
图3 I=100 时模型仿真结果

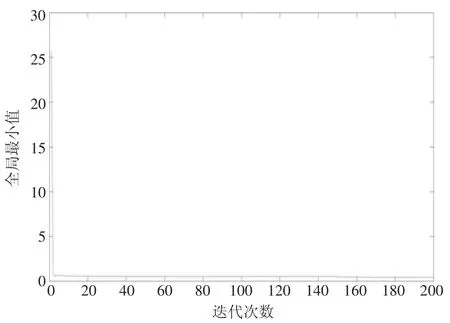
图4 I=200 时模型仿真结果

图5 I=500 时模型仿真结果

根据以上结果可以分析得出：

迭代50 次得到的零部件最优分配方案为：b=45、b=40、b=50、b=32、b=26、b=44、b=49、b=60、b=35、b=24、b=35、b=40、b=50、b=36、b=20。

此时上层目标函数值为F(b)：0.586。

迭代500 次得到的零部件最优分配方案为：b=46、b=38、b=47、b=39、b=24、b=33、b=27、b=33、b=36、b=18、b=40、b=30、b=30、b=25、b=20。

此时上层目标函数值F(b)为：0.486。

综合分析可以看出，当取I=500 时，所购买的零部件资源r、r、r几乎全部分配完，资源r、r存在部分剩余，因此为避免增加成本应不再购买并且分配该资源，此时目标函数达到最优值。

根据上述模型求解得出上级决策者分配给下级部门的资源数量。选取迭代500 次时结果，并且针对第一个部门A 得出资源消耗如表2 所示：

表2 部门A 资源使用情况

由于消费市场变化莫测，产品的市场需求也难以预估。假设某个周期消费者对该4S 店中的三种车型(n,n,n)的需求量x分别为(12,8,6)，根据上述表格可以求得资源r刚好能够满足市场需求；零部件资源为r、r富余状态，可以租出的剩余资源数为h=8、h=5；资源r、r则出现短缺现象，需要经过横向补货租进的数量分别是S=1、S=26。对其资源拥有量b进行优化，可以得到α,α,…,α,β,β,…,β的取值均为0，并且取值会随着市场需求的变化也相应改变。具体变化如表3、表4所示。

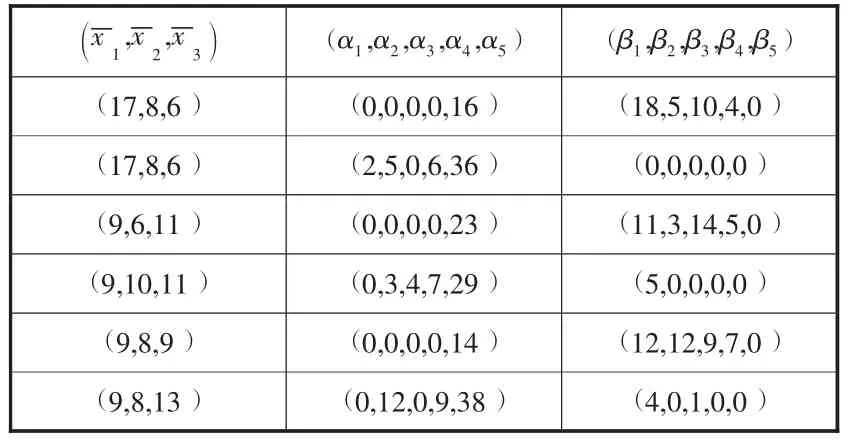
表3 市场需求变化对配件服务能力的影响

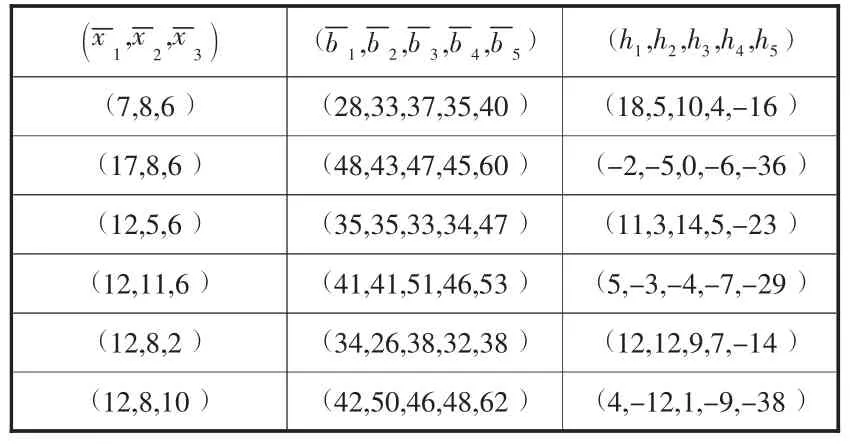
表4 市场需求变化对零部件资源数量的影响

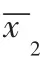
对于配件n而言，资源r是组成该配件的核心部件。由于资源r是刚好可以满足市场需求，因此只有当市场需求水平降低时，该资源才能变为富余的状态，从而可以租出，否则都会短缺，因此部门可以准备周期内多储备一些零部件资源r，从而提高市场竞争力和持续发展能力。

4 结论

汽车配件服务企业资源分配与交易的决策问题，本文首先针对汽车配件服务企业上下级决策者关系，建立了资源分配两层决策模型，并通过使用粒子群算法进行求解，得出了在上下级决策者之间相互制约的情况下，上级决策者资源分配的最优解；此外，为了提高企业服务水平，本文在满足市场需求的前提下，分析汽车零部件资源的交易特点，建立了基于市场需求的优化模型，并构建了关于资源自有量的线性规划逆优化决策模型。示例体现了汽车配件服务企业下层决策者在给定资源量的前提下，如何与其他部门或企业进行零配件资源的交易，从而实现资源的精益化与成本最小化。