高铁运输参与的多目标绿色多式联运路径优化
梁晓磊,刘星雨,李文婷,马千慧,梅 磊
(1.武汉科技大学 汽车与交通工程学院,湖北 武汉 430065;2.江汉大学 智能制造学院,湖北 武汉 430056)
0 引言
我国交通运输在“碳达峰、碳中和”要求下,高铁作为一种具有耗时少和安全性高的高效运输模式,探究“高铁+”联运模式,优化绿色发展要求下的高铁多式联运,成为构建绿色“高铁经济带”需要解决的问题。目前针对多式联运问题模型,众多学者进行了研究,主要集中于不同场景下的多式联运模型构建,如针对不同产品价值特性构建的总物流成本最小化模型、结合联运网络枢纽选址构建的总费用最小化模型、考虑长江经济带现状的运输成本和时间最小化模型、到达时间间隔约束下的运输成本和转运成本最小模型、随机运输时间与班期限制的多式联运模型等。近年来碳排放控制也成为多式联运的重要目标,如Li 等考虑多任务碳排放构建了多式联运路径优化模型,刘杰等构建了运输总成本和运输碳排放量最小的多目标优化模型,李珺等构建了考虑运输时间、中转时间、客户需求和中转集拼货运量的绿色多式联运路径优化模型,Guo 等针对收货时间约束和运输方式选择等特征建立了碳排放和运输成本最小化双目标模型。
目前大部分多式联运网络建模仅考虑公路、普通铁路、水路,而对高铁多式联运网络研究多集中在铁路规划设计方面,针对多式联运路线规划研究较少,如考虑不同高铁线路产能的高铁网络适应性分析、高铁站与公交接驳设计、高铁参与下的生鲜农产品配送总成本最小等。实际上,由于高铁不如普通铁路进行大宗货物运输,对发车时间也有非常严格要求,因此运量和时间因素对高铁参与的多式联运网络路径选择有重要的影响。本文以高铁参与的多式联运网络为对象,从绿色经营角度,考虑运力、班期及运输质量等因素,综合碳排放量、运输成本和物流服务满意度构建多目标绿色多式联运路径优化模型和求解算法。
1 问题描述与模型构建
1.1 问题描述
本文中多式联运运输考虑各节点处不同运输方式班期和运力差异以及收货时间窗约束。起止点间有若干个转运节点,任意相邻节点间具有公、水、普铁、高铁运输方式可选,其中运输和中转换装过程中存在碳排放。除公路外,各节点处不同运输方式受班期和运力限制。在多式联运过程中作如下设定:
(1)运输过程中同批货物不可拆分。若货运量超过所选节点最大运力,需选择其他节点;
(2)若货物在班期外到达,需等待下一班期;若超过节点某运输方式最大运力,不能采用该方式;
(3)任意相邻节点间只能选择一种运输方式,同一节点最多进行一次中转;
(4)任意相邻节点至少存在一种运输方式,同种方式不进行换装。
1.2 符号定义
设O、D 代表起始点城市;W 表示节点城市集合;M 表示运输方式集合;Q 表示承运集装箱量。
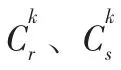
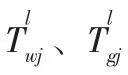
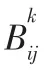
满意度变量:o表示利用模糊等级评价法求解的节点i 到j 间的物流服务质量;H、H和H表示多式联运时效性、经济性和服务性评价指标;C、C表示最小和最大运输总成本。

1.3 模型构建
根据上述问题描述,考虑节点运力、混合时间窗等因素,以运输成本、碳排放量和物流服务满意度为优化目标构建模型。
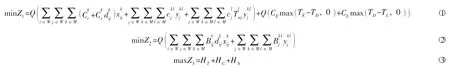
目标1(式(1))由运输费、中转换装费、等待转运仓储费以及违反顾客时间窗的惩罚费组成的总运输成本最小化。目标2(式(2))为最小化碳排放量,包括运输和转运过程中的碳排放量。目标3(式(3))物流服务满意度最大化,包括时效性、经济性和服务性评价。总运输时间T包含运输、转运、等待转运及等待离开等时间,如式(4)所示。

在运营过程中,货物提前或延期到达会导致存储费用产生以及降低客户满意度。本文对多式联运时效性评价与运输时间的关系采用模糊理论中升岭形与降岭形函数进行表征,如式(5)所示。

对于多式联运经济性评价与运输总成本的关系采用隶属度函数来描述,其特征可以表征成本波动对经营人满意度的影响,如式(6)和式(7)所示。目标总成本Z 由运输成本和碳排放成本组成。
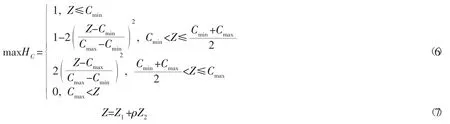
多式联运服务性评价指标与各节点的基础设施水平、经济发展水平以及多式联运物流服务水平相关,采用模糊等级评价如式(8)所示:

约束条件:

式(9)表示节点i 与j 之间只能选择一种方式;式(10)表示在节点j 处最多发生一次转运;式(11)保证整个运输过程连续;式(12)保证节点流量平衡;式(13)表示决策变量;式(14)表示节点运输能力约束;式(15)表示在节点j 处等待转运耗费时间;式(16)表示在节点j 处等待离开耗费时间。
2 基于多目标进化算法的问题求解设计
在上述模型中,目标间存在一定冲突,如当运输成本最小时,会使运输时效性及服务性变差;最小化碳排放方案需要降低转运环节碳排放,也会带来仓储和惩罚成本增加,无法在优化单一目标的同时不削弱其他目标,因此该问题属于多目标优化问题。针对两个目标以上的多目标问题,基于参考点的非支配排序遗传算法(NSGA-Ⅲ)具有较好的求解效果。但实际应用中当最优解数量未知时,真实非支配解数与种群规模的差异会导致NSGA-Ⅲ算法在非支配排序过程中存在“漏解”现象,削弱了算法搜索能力。因此,本文利用自适应交叉变异算子和外部非支配解保留策略构建改进INSGA-Ⅲ(Improved NSGA-Ⅲ),结合基于优先级的编码解码策略对模型进行有效求解。改进策略描述如下:
(1)基于优先级实数编码和解码策略设计
多数研究采用实数和整数的方式分别对多式联运运输路径和运输方式编码,使染色体较长,带来解码、交叉和变异操作复杂。本文设计基于优先级的实数编码策略对运输路径和方式进行一体化编码,提高解码效率。以具有4 种运输方式和6 个节点的多式联运网络为例,染色体长度设置为节点数6,取值范围为[1,5)。每个基因位数值代表节点运输优先级,其整数部分为1~4 的数值,分别代表公路、水路、普铁及高铁。
针对图1 中染色体编码,起始点为节点1,根据优先级和可达节点确定下一节点。譬如节点1 的可达节点有2 和4,而节点2 的优先级值高于节点4,因此选择路径1→2,同时运输方式采用节点2 优先级值取整为3 即普铁。依此类推,最终所得路径为1→2→3→6,节点间运输方式为3-4-1。如出现节点间所选运输方式不存在时,则优先选择公路。

图1 染色体编码图
(2)外部非支配解保留和自适应交叉变异概率策略
利用非支配排序将种群分为若干个不同的非支配层。根据非支配层等级顺序和参考点关联性选择将各非支配层的解逐层加入到新的种群,直到种群内个体数满足预设定种群大小。同时,为了避免非支配解在迭代过程中丢失,建立一个外部非支配解集。从每一代排序等级为1 的非支配解中挑选新的不重复非支配解到外部非支配解集中,并对外部解集中保存的上一代解进行非支配更替,实现外部非支配解集更新。
为增强算法搜索性,分别引入自适应的交叉和变异扰动策略,增强种群全局搜索能力。交叉和变异方式分别以模拟二进制交叉与多项式变异为基础,设定自适应交叉和变异概率如式(17)和式(18)所示。其中,p为交叉概率,p为变异概率,γ、ε 表示常数,δ 是以e 为底在区间[-10,0]内的指数分布随机数,N 表示最大迭代次数,i 为当前代数。

3 实验设计与分析
3.1 案例设计
假设20 个20ft 集装箱需从城市1 运往城市20,有18 个可选中转节点。任意相邻节点间至多有公路、水路、普铁、高铁4种运输方式,如图2 所示。除公路外,其余运输方式有班期限制。设置初始顾客收货时间窗为[40,55]。货物提前到达的单位存储成本和延迟到达的单位惩罚成本分别是600 元/(TEU·h)和1 200 元/(TEU·h)。公路运输基价为20 元/TEU,运输运价为3元/(TEU·km)。水路运输基价为8 元/TEU,运输运价为0.429 元/(TEU·km)。普铁运输基价为161 元/TEU,运输运价为0.6603元/(TEU·km)。高铁运输基价为260 元/TEU,运输运价为1.29 元/(TEU·km)。碳税税率为20 元/t,其中,公路运输单位碳排放量为0.9kg/(TEU·km),水路为0.328kg/(TEU·km),普铁为0.238kg/(TEU·km),高铁为0.198 kg/(TEU·km)。水路、普铁、高铁的单位时间等待成本分别为40 元/(TEU·h),60 元/(TEU·h),100 元/(TEU·h)。多式联运服务性评价指标中节点基础设施建设、经济发展水平以及物流服务水平的对应权重分别为{0.2,0.2,0.6},评价等级为三级,对应分值为{0.9,0.6,0.3 },采用模糊等级法随机生成18 组节点服务性评价数据。各路径对应不同运输方式的运输时间、距离和运力如表1 所示,不同运输方式间单位转运费用、转运时间、单位中转碳排放量如表2 所示,班期设置如表3 所示。
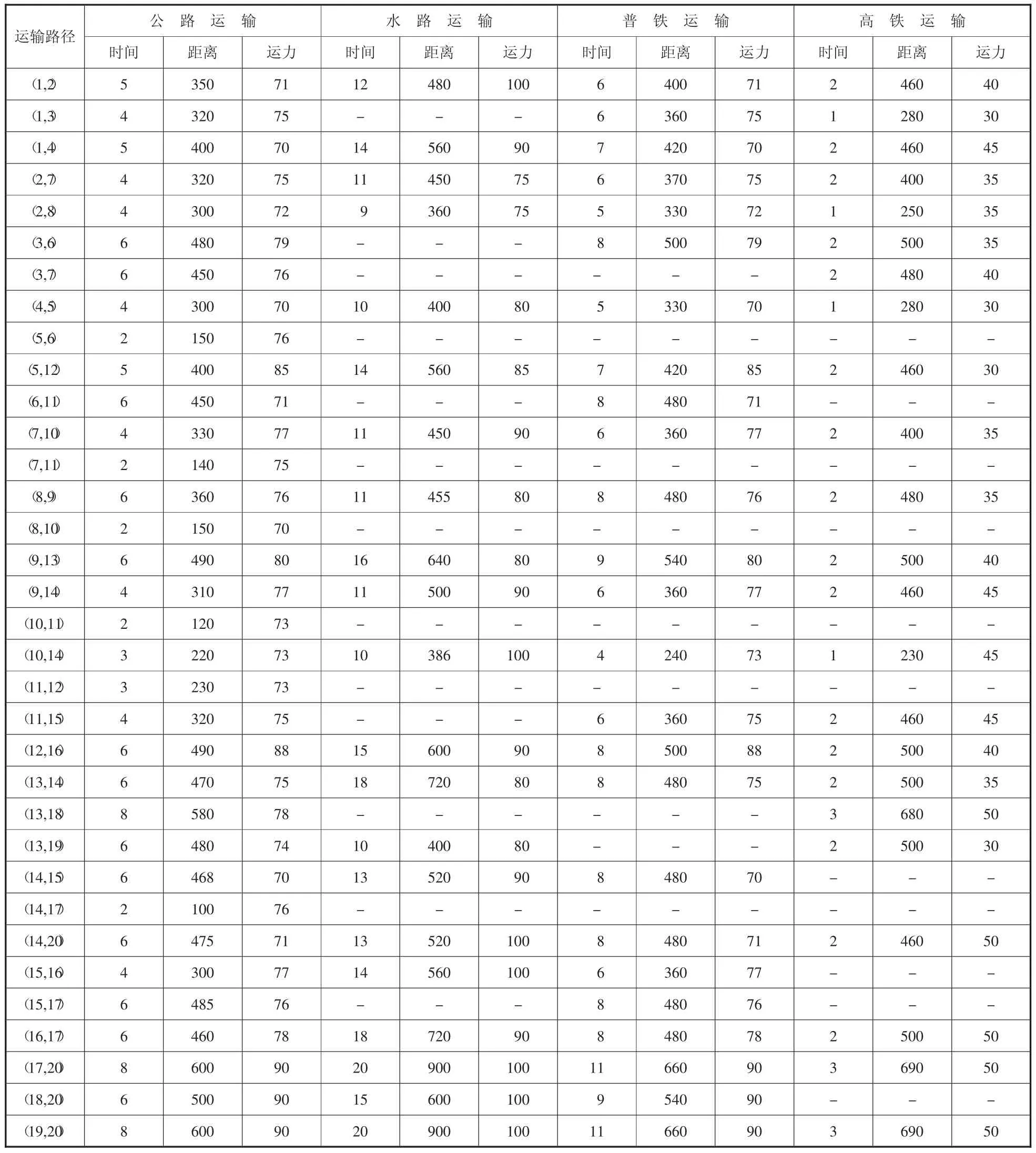
表1 各运输路径不同运输方式下的运输时间(h)、距离(km)和运力(TEU)

表2 各运输方式间单位转运费用、转运时间和单位中转碳排放量

表3 各运输方式在转运节点处的班期限制
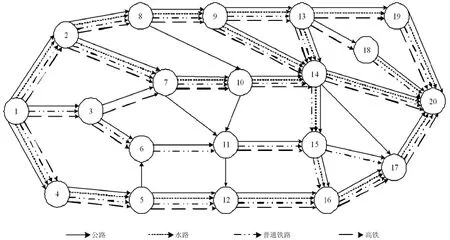
图2 多式联运运输网络图
实验中算法种群规模为100,最大迭代次数为100,初始概率p=0.9,p=0.5,扰动因子r=1、ε=0.5。采用Python3.8 进行算法编程实现,运行平台为Intel Core(TM)i5-4200H 2.80GHz CPU,4.0G ROM。
3.2 结果分析
(1)算法和模型有效性分析
本实验采用NSGA-Ⅲ算法和INSGA-Ⅲ算法对所构建模型进行求解和对比,以验证算法和模型的有效性。两个算法获得的Pareto 解集空间分布(如图3 所示)对比显示INSGA-Ⅲ算法所求非支配解数量更多、分布区间更广,表现出了良好的多目标搜索性能,验证了改进算法的有效性。基于表4 中运输成本最小、碳排放量最少和物流服务满意度最大的Pareto 解集,对比方案1 和方案3,不采用高铁运输,虽运输成本减少,但是碳排放量和运输时间增加,物流服务满意度下降约37%;对比方案2和方案3,采用单一高铁方式进行运输,虽然碳排放量和运输时间明显减少,但是运输成本上涨9 倍且物流服务满意度下降。说明合理安排高铁参与货物运输,有助于节省运输时间、减少碳排放量并提高物流服务满意度,验证了多目标优化模型的适用性。

表4 各目标最优Pareto 解集
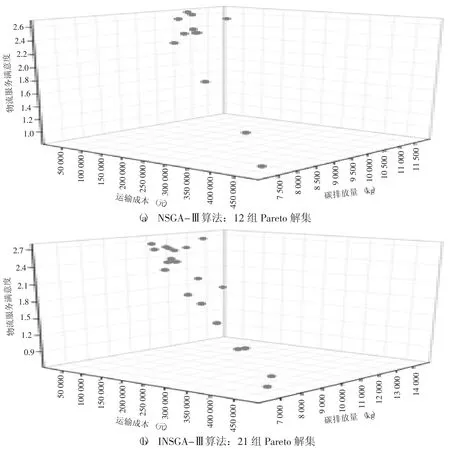
图3 Pareto 解集空间分布图
(2)运量变化对多式联运路径优化影响分析
运量大小对高铁参与的运输路径选择有重要影响,本实验以5TEU 为增量构建算例。由图4 可知,针对不同运量下运输成本最小化目标,随运量增加,运输成本和碳排放量呈正相关,而运输时间和物流服务满意度保持不变。结合表1 和表4 结果分析可知,因为运量变化没有超过运输成本最小化方案的路径服务能力,运输路线与运输方式没有发生改变。在不同运量下的碳排放量最小化结果(如图5 所示)中,当运量大于30TEU 时(实验4~7),运输成本变化显著,运输时间增加,物流服务满意度上升。其原因是运量超过单一高铁运力,运力大、运输成本低但运输时间长、碳排放量高的方案被选取。在物流服务满意度最大化方案中(如图6 所示),运量大于35TEU 时运输成本增长变缓,碳排放量和物流服务满意度下降,运输时间缩短,原因是运量超过该网络最大化物流服务满意度方案的服务能力,运力大但物流服务满意度低的方案开始被选择。实验可知,在一定物流服务满意度范围内,相比单一使用高铁带来的时效性与低碳效益,运输成本的变动影响更重要,选择高铁与其他运输方式的联运发展对于提高整体物流效益更有优势。
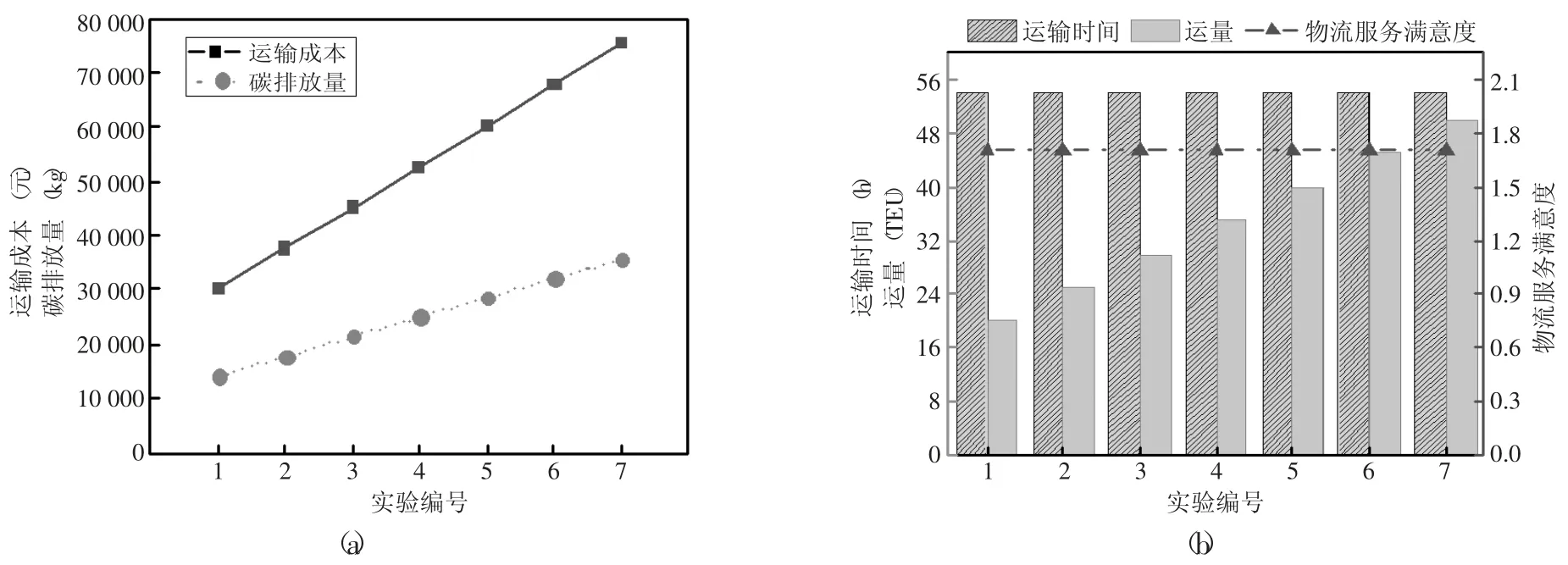
图4 不同运量方案下最小运输成本值变化图
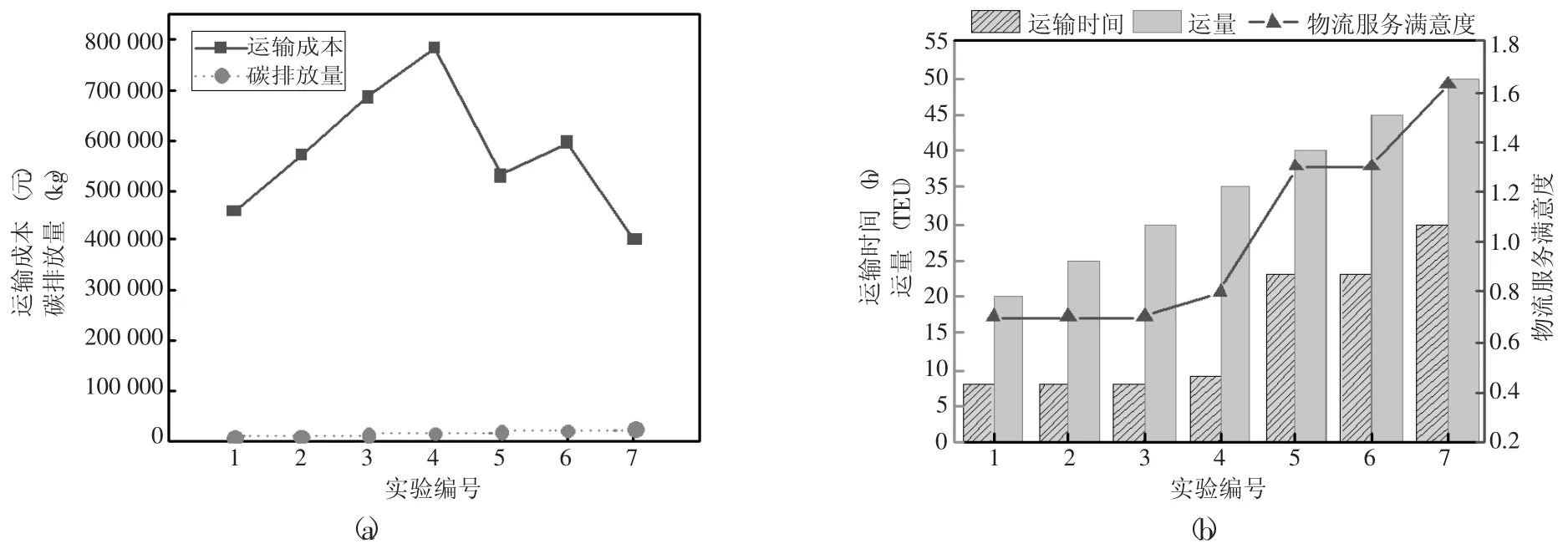
图5 不同运量方案下最小碳排放量值变化图
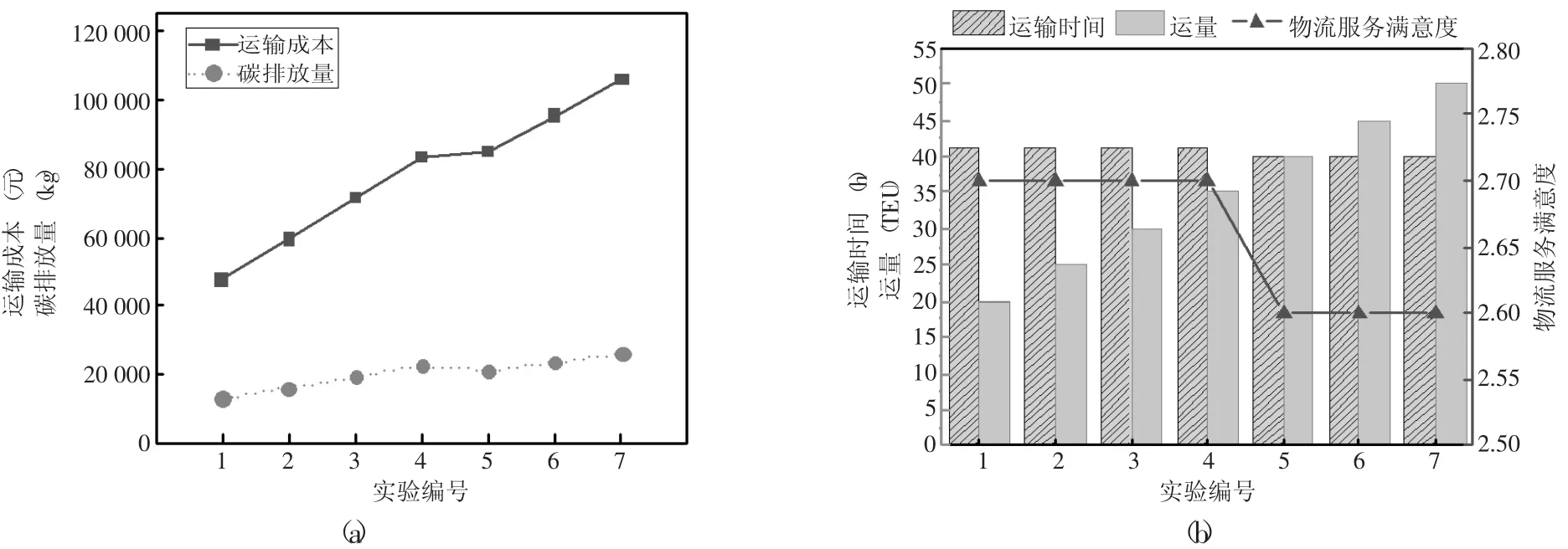
图6 不同运量方案下最大物流服务满意度值变化图
(3)时间窗变化对多式联运路径优化影响分析
在顾客收货时间窗[40,55]基础上,以5h 为增量,增加[25,40]、[30,45]、[35,50]、[45,60]案例进行时间因素影响实验。实验结果如图7 所示,其中由具有高铁或普铁的运输方案数量在所有案例所得非支配解中占比(图7(a))分析可知,普铁参与率一直维持较高水平,但随着时间窗不断提前,高铁参与率逐渐上升。通过高铁联运和普铁联运方案在所有包含高铁或普铁的非支配解中数量占比(图7(b))分析可知,当顾客时间窗延后至[45,60]时,普铁运输具有显著优势,高铁参与率低且大多以联运方式为主。当时间窗提前至[35,50]时,普铁参与率达到87.5%,高铁参与率上升,此时单一普铁运输利用率达到最高。当收货时间窗进一步紧缩,提前至[30,45]时,高铁参与率超过70%,联运参与率下降约9%,普铁参与率下降,此时高铁取代部分普铁进行单一或联合运输。当时间窗提前至[25,40]时,高铁与普铁参与率及联运参与率均呈现上升趋势,高铁与普铁联运成为主要方式。因此,当顾客收货时间窗大幅提前时,在现有多式联运网络条件不变下,促进高铁和普铁联运是主要方案。
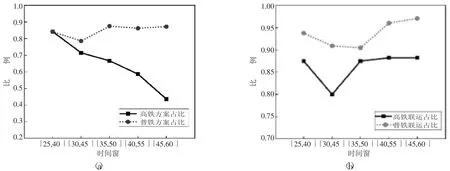
图7 不同时间窗下运输方案占比图
4 结束语
考虑碳排放和高铁运输对多式联运的影响,本文引入节点运力差异以及混合时间窗因素,构建了具有高铁参与,以运输成本、碳排放量和物流服务满意度优化为对象的多目标绿色多式联运模型,并采用具有优先级的实数编解码策略以及基于自适应交叉变异算子和非支配策略的INSGA-Ⅲ算法进行求解,通过算例验证了算法和模型有效性。
针对普铁运输和高铁运输在多式联运中的竞争协作,通过对不同货运量和时间窗两类重要影响因素的实验分析,结果表明,当顾客时间窗后延或运量超过高铁线路运力限制时,相较使用单一高铁运输对低碳、时间等效益的提升,经济效益降低更为显著,需在合理物流服务满意度内选用以高铁为辅的联运模式进行货物运输;而当顾客时间窗持续提前或运量较小时,随着时间窗不断提前,高铁带来的时间负效益逐渐转化为经济正效益,适合采用高铁为主的联运模式,上述结论可为多式联运运营者决策提供支持。
——《2013年中国机动车污染防治年报》(第Ⅱ部分)

