基于点面接触的三维结构地震接触模拟

钟 红，郭胜山，涂 劲，李德玉，王海波

（中国水利水电科学研究院 工程抗震研究中心，北京 100048）

1 研究背景

接触问题是土木水利工程中的重要非线性问题。工程地基中存在大量的节理、裂隙和断层等不连续面，在外荷载尤其是地震作用下可能产生相对滑移和错动[1-3]。混凝土拱坝中设置有横缝，强震时可能张开从而引起应力重分布，拱向应力释放而梁向应力增加[4-9]。对工程结构-地基系统在地震荷载作用下可能出现的接触问题进行准确的模拟，影响到结构抗震安全评价的可靠性，直接关系其抗震安全。

在基于有限元方法的接触问题模拟中，接触体经有限元剖分后，其表面被离散化为多边形边界单元集，接触体之间的接触相互作用转化为离散的分片光滑的表面接触单元作用，产生接触作用的点对即为接触点对。对于工程结构在地震作用下的接触分析，由于接触体之间可能出现大滑移、大转动，使得在问题解决之前无法预知其局部接触状态，如何有效、准确地搜索出每一时刻的接触点对成为接触问题求解的关键。在结构产生大滑移的情况下，初始构型发生变化，接触点对位置相应发生变化，小变形接触算法中常用的点点接触（Node-to-Node，NTN）模型是不成立的[5-9]。主从算法采用点面接触（Node-to-Segment，NTS）方式进行搜索，由于能实时捕捉接触位置，在大变形接触搜索中被普遍采用，而且被认为是比较有效的搜索算法之一[10-12]。

本论文将点面接触模型引入基于动接触力法的接触模拟分析，实现了对三维结构地震大滑移接触的模拟，并与点点接触模型进行了比较研究。

2 接触搜索

接触搜索的任务是找出系统中的测试对，然后针对每个测试对确定其接触状态，包括接触、贯入、脱开。对于接触和贯入的情况，测试对已经转变为实际的接触对，还要找出接触点及贯入量。上述寻找测试对的过程，称为全局搜索；确定测试对的接触状态以及计算接触点和贯入量的过程，称为局部搜索。全局搜索算法的关键是计算效率，局部搜索算法的关键是计算精度。

全局搜索算法目前使用较普遍的全局搜索算法主要包括主从算法、单曲面算法、级域算法、位码算法等。点面配对的主从接触算法中，将主片上的节点被定义为主节点（master node），从面上的节点被定义为从节点（slave node）。对于每一个从节点，搜索出与之对应在主片上的接触点，从而形成接触点对。为了提高接触搜索的计算效率，在进行接触搜索细判之前常常要对表面单元进行粗判，排除一部分不可能发生接触的表面单元。

对于拱坝横缝、地基内部结构面、坝基交界面等接触面的地震滑移模拟，接触形态相对明确，滑移量相对较小，全局搜索依据有限元拓扑结构开展。在结构地震响应计算开始前，根据结构初始拓扑结构，针对每一对接触面上的从节点，在主接触面上寻找与之对应或者距离最近的节点，记为O节点（见图1）。对于主从面上节点位置重合的情况，这一过程可简化，直接选取坐标相同的对应节点即可。进而将与O点共单元且位于接触面上的节点A～H所包围的区域（红色线包围的Layer1区域）作为该从节点的可能接触范围。如预判滑移量过大可能超出此范围，则可将该范围外推一层单元，并将绿色虚线包围的Layer2区域作为可能的接触范围。

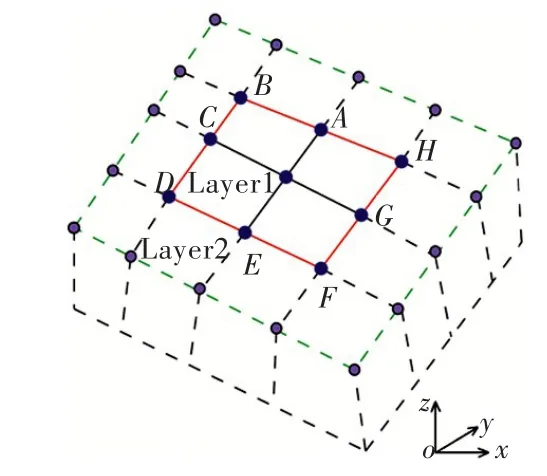
图1 全局搜索示意图

局部搜索的目的是从全局搜索给定的接触测试对中确定真实发生的接触（从节点，主接触片）对，并计算相应的间隙函数值。为避免经典点面算法存在的盲区问题以及提高搜索效率，本文采用内外算法[13]，以从节点的外法线方向作为从节点对主接触片的投影方向（同时也是接触力施加方向）。从节点外法线方向定义为与该节点相连的接触片法线方向的平均值，如图2所示。

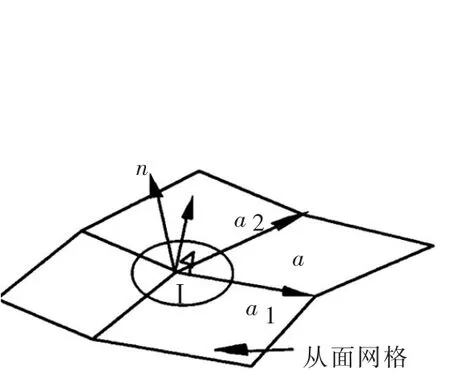
图2 从点的外法线方向[13]

其中na为单元a在图中所示面上的外法线方向，由两个方向矢量a1和a2作叉积得到。

从节点相对于主接触片一条边的内或外状态，通过从节点与该边构成的三角形在主接触片上的投影来确定，如图3所示。

图3 从节点的内外状态检查

其中rab和rad是三角形的两条边的方向矢量。

若Δa≤0，则从节点处于边内部。如果从节点处于主接触片所有边的内部或者外部，则从节点位于该主接触片内部，否则位于主接触片外部。

如果从节点位于主接触片内部，则利用下式计算从节点对主接触片的贯入量

式中x为投影点，xs为从节点位置向量。

内外算法的优势在于，接触点可以唯一确定，避免了从节点对主接触片的多重接触，并且接触点计算不需要迭代。因此，该算法具有很好的健壮性与较高的计算效率。由于内外算法假定接触点处主从面的法向共轴（但方向相反），当从节点位于两个低阶单元的交界线上时，尤其是当网格不够精细时，内外算法给出的接触方向可能会与实际存在较大偏差。

接触点确定后，通过如下步骤求解其坐标。在主接触片上建立二维直角坐标系（图4），主点1的坐标通过求解从节点x2在面ABCD上的投影获得，其与节点坐标存在如下插值关系：

图4 点面接触示意图[11]

3 基于点面接触的动接触力模型

4 楔形体动力稳定模拟

将本文算法应用于边坡的滑动模拟。E.T.Hoek和J.W.Bray的楔形体稳定问题[14]典型算例中，楔形体边坡面CDEF的倾角为65°，倾向为185°，坡顶面ABCD的倾角为12°，倾向为195°。边坡被斜面abc和斜面adc交切，楔形体abcd表面的产状和摩擦参数见表1。平面abc和adc交线ac的垂直高度H=39.624 m。岩体重度γ=2.563×103kg/m3。楔形体及有限元模型见图5和图6。有限元模型中地基的模拟范围为从楔形体往外边界延伸80～100 m。

图5 Hoek楔形体示意图

图6 有限元模型

表1 楔形体各表面的产状和摩擦参数

先考虑楔形体承受自重的情况。基于强度折减法计算其安全系数，当减小滑面内摩擦角及黏聚力时，楔形体失效下滑，安全系数为1.60。文献[15]中采用DDA和有限元法计算的安全系数分别为1.66和1.68，本文结果与之一致。

地震工况中，输入Koyna地震加速度时程，其中水平向分量沿y轴输入，竖直向分量沿z轴输入。图7中给出了归一化的地震加速度时程，考虑了加速度幅值为0.2 g、0.5 g、0.8 g、1.0 g和1.5 g等五种情况。

图7 Koyna地震加速度时程（归一化）

图8—图10给出了楔形体在加速度幅值为1.0 g的地震动激励下的破坏模式以及滑移量、位移时程，并将采用点面接触模型（NTS）的结果与点点接触模型（NTN）的结果进行比较。两种接触模型得到了相同的破坏模式，楔形体沿两个结构面相交的棱线滑动（图8）。楔形体约在2.4 s后开始滑动，地震激励结束时楔形体保持稳定，根据点点接触模型计算得到的P1点三向残余位移分别是5.6 cm、-11.3 cm和-8.2 cm，相应地根据点面接触模型的计算结果为7.2 cm、-14.3 cm和-10.2 cm，比前者分别增大27.1%、26.3%和24.7%（图9）。

图8 楔形体破坏模式

图9 地震激励下楔形体A点位移时程（1.0 g）

图10 地震激励下楔形体B点滑移量时程（1.0 g）

以P2位置两点沿两结构面相交棱线方向的位移之差作为楔形体的滑移量。从图10可看出，随着地震动的增强，2.4 s后楔形体产生明显的滑动，之后滑移量出现数次阶跃式增大，最终保持稳定。由点点接触模型和点面接触模型计算得到的残余滑移量分别为14.7 cm和18.6 cm，后者比前者大26.5%。

图11比较了不同加速度幅值的地震动输入时的滑移量值。当加速度幅值在0.5 g及以下时，楔形体没有明显滑动。随着地震加速度幅值的增大，用两种接触模型计算得到的滑移量都增大，且点面接触模型算得的滑移量大于点点接触的滑移量，且二者差别随着加速度幅值的增大而增大。这是由于点面接触模型中，每一时刻都根据变形后的坐标重新判断接触关系，可更真实地反映接触状态。

图11 不同地震加速度幅值时的滑移量

5 考虑横缝开合效应的拱坝地震响应分析

以某拱坝为例，研究了在拱坝地震响应分析中采用点面接触模型的效果，并与点点接触模型进行了对比。大岗山拱坝高210 m，地基模拟范围为2倍坝高，采用无质量地基模型模拟。拱坝-地基系统的有限元模型如图12所示。大坝共设置28条横缝，从左向右依次编号1～28。混凝土的弹性模量、泊松比和密度分别为24 GPa、0.17和2400 kg/m3，横缝的摩擦系数取0.8，黏聚力取0 MPa。基岩的弹性模量、泊松比和密度分别为24.5 GPa、0.25和2000 kg/m3。设计地震加速度为0.5575 g，考虑了1倍、2倍、3倍设计地震输入的情况，地震动时程沿三向输入。

图12 拱坝-地基有限元模型和横缝位置

图13给出了所有横缝在整个时程中的最大开度。1倍和2倍设计地震加速度输入时，可看出各条横缝的开度并不均匀，边缝和中缝的开度较大。采用点点接触模型（NTN）和点面接触模型（NTS）计算的结果基本相同。3倍设计地震加速度输入时，各缝开度显著增大，但各缝开度趋于均匀。最大开度出现在左岸坝肩附近，且点面接触模型计算结果比点点接触模型的结果大4.0%。对于中缝，点点接触模型的开度更大。由于横缝的接触非线性，随着地震加速度的增大，各缝开度增长幅度超过地震动增长的幅度。1倍、2倍、3倍设计地震动输入时，采用点点接触模型计算的最大开度分别是21.1 mm、56.9 mm、100.9 mm，而采用点面接触模型计算的最大开度分别是21.0 mm、56.9 mm、104.9 mm。

图13 横缝最大开度

图14给出了所有横缝在整个时程中的最大切向滑移量。1倍和2倍设计地震加速度输入时，采用点点接触模型（NTN）和点面接触模型（NTS）计算的结果基本相同。3倍设计地震动输入时，左右两侧坝体的横缝滑移量大体上呈对称分布，最大滑移量出现在两侧的四分之一拱圈处。采用点面接触模型算得的滑移量比点点接触模型大8.8%。

图14 横缝最大切向滑移

上下游坝面对最大主拉应力云图和最大主压应力分布云图分别见图15和图16。对于最大主拉应力，两种接触模型得到的应力分布趋势一致，最大值出现的位置相同。点面接触模型和点点接触模型算得的最大应力分别为20.7 MPa和18.7 MPa，前者高出10.7%。对于最大主压应力，两种接触模型算得的应力分布趋势基本一致，最大值出现位置有所差异。点面接触模型的最大值（-39.6 MPa，负号代表受压，下同）出现在左岸坝肩，点点接触模型的应力最大值（-31.7 MPa）靠近下游面底部，且前者比后者高出24.9%。

图15 3倍设计地震动输入时最大主拉应力分布（单位：Pa）

图16 3倍设计地震动输入时最大主压应力分布（单位：Pa）

6 结论

针对工程结构在地震作用下产生大滑移如边坡滑动、拱坝横缝张合等接触模拟问题，提出了基于点面算法和动接触力模型的接触算法，相对于点点算法能更真实地反映接触位置并且适用于接触面网格不一致的情况。推导了适于点面接触的动接触力模型公式；采用主从接触算法，通过全局搜索和局部搜索确定接触点对，其中局部搜索中采用内外算法可避免盲区问题、提高搜索效率。

通过楔形体稳定问题对该模型进行了验证，并通过对楔形体进行地震动输入研究了其地震稳定问题，比较了采用点点接触和点面接触的计算结果。研究表明，地震加速度幅值较小时，两种接触模型结果一致，随着加速度幅值的增大，结构响应增大，两种接触模型的计算结果差异也随之增大，地震加速度幅值为1.0 g时残余滑移量差别可达25%左右。

将该模型应用于某拱坝的地震响应分析，模拟了28条横缝，并考虑了1倍、2倍和3倍设计地震动输入的情况。研究表明对于1倍和2倍设计地震动输入的情况，点面接触和点点接触模型计算结果基本一致。对于3倍设计地震动输入的情况，两种接触模型得到的横缝开度、切向滑移量以及最大应力分布趋势大体一致，但点面接触模型算的最大横缝开度、最大切向滑移量、最大主拉应力、最大主压应力均大于点点接触模型的计算结果，增大幅度分别为4.0%、8.8%、10.7%和24.9%。可以看出，对于相对较小的地震，点点接触模型即具有足够的精度，对于超强地震，点点接触模型的计算结果偏小，尤其对应力值的低估更为明显。