混凝土大坝变形监控指标拟定的混合法
徐小枫,黄耀英,朱赵辉,李 新
(1.三峡大学 水利与环境学院,湖北 宜昌 443002;2.中国水利水电科学研究院,北京 100038;3.新疆额尔齐斯河流域开发工程建设管理局,新疆 乌鲁木齐 830000)
1 研究背景
大坝变形(位移)监测反映了大坝整体变形和受力性态,且变形监测直观可靠,因此,大坝变形监测是大坝重要的安全监测项目。在大坝蓄水运行期,由于监控指标对于判定大坝监测物理量是否异常十分方便,在设计阶段或当获得足够的监测资料时,经常分析求得相应的监控指标。拟定监控指标的主要任务是根据大坝系统(坝体和坝基)已经历荷载的抵御能力,来评估和预测抵御可能发生荷载的能力,从而确定各荷载组合下大坝服役性态效应量的警戒值和极值[1]。由大量工程经验和实验成果分析表明,混凝土大坝的结构性态可分为黏弹性、黏弹塑性和失稳破坏3个阶段,因此,大坝安全可分为正常、异常和险情,对应地将监控指标划分为一、二、三级[2]。迄今国内外广大科技工作者开展了大量变形监控指标的研究,这些变形监控指标的拟定方法主要分为两大类[3]:一类是基于变形监测资料拟定监控指标,主要包括置信区间法、典型效应量小概率法以及云模型法等[4-7],此类方法虽然简洁易行,但其可信度依赖于现有监测资料所包含的荷载信息,而且物理概念不明确,没有联系大坝失事的原因和机理[5];另一类是基于结构分析的数值计算法或数值计算-变形统计模型的混合法拟定监控指标,该类方法物理概念较明确,可模拟未发生过的不利工况,同时也可充分利用监测资料。其中,在采用数值计算-变形统计模型的混合法拟定变形监控指标时,首先依据超载法或强度储备法(或称强度折减法)[8-9],采用数值计算法计算一部分相对可靠的效应量,其余效应量则采用统计模型的分离值,进而累加获得变形监控指标。例如,顾冲时等[2]基于6参数强度准则,采用有限元法计算了最不利水压分量与温度分量,采用变形统计模型计算时效分量,拟定了佛子岭连拱坝的变形二级监控指标;刘健等[10]基于4参数强度准则、Mohr-coulomb准则和D-P准则[11],采用有限元法计算了水压力、泥沙压力、温度、渗流力等荷载引起的效应量,而时效分量则由统计模型分离获得,从而拟定了李家峡拱坝的变形二级监控指标。由于温度分量和时效分量的数值计算涉及到的材料参数和边界初始条件较为复杂,魏超等[12]、尹尧等[13]、Chen 等[14]、魏博文等[15]等只对水压分量采用有限元法进行计算,而温度、时效分量则由统计模型分离获得,结合实际混凝土坝工程拟定了相应的变形监控指标。其中,在进行结构力学数值计算时,对于材料弹性模量取值问题,尹尧采用了竣工设计报告的参考值,魏超采用假设试算法来获得当前实际材料强度参数,顾冲时、Chen和魏博文则采用了反演参数值;而对于材料强度参数取值问题,目前报导的文献一般是采用强度极限值或设计报告的建议值。总体来看,由于监控指标拟定涉及参数众多且不易合理确定,完全采用数值计算法来拟定监控指标报导文献很少;而采用数值计算-变形统计模型的混合法拟定二级监控指标时,存在对变形统计模型分离的不利温度分量的非线性效应考虑不足的问题;此外,材料强度参数以及安全储备系数(或强度折减系数)等的取值也较为含糊。
为此,本文采用数值计算-变形统计模型的混合法拟定变形一级、二级监控指标时,着重考虑了不利温度分量的非线性效应,以及尝试引入材料性能分项系数,明确材料强度参数以及安全储备系数(或强度折减系数)等的取值,并结合某常态混凝土拱坝进行变形一级、二级监控指标拟定应用。
2 混凝土坝变形监控指标拟定原理
2.1 混凝土坝变形监控指标拟定准则通常混凝土坝变形统计模型由水压、温度和时效分量组成[1]。当拟定混凝土坝变形一级监控指标时,在不利荷载工况下,大坝处于黏弹性工作状态,此时采用弹性参数计算水压分量和温度分量,采用黏弹性参数计算时效分量。当拟定混凝土坝变形二级监控指标时,在不利荷载工况下,大坝处于黏弹塑性工作状态,此时采用弹塑性参数计算水压分量和温度分量,采用黏弹塑性参数计算时效分量。因此,混凝土坝变形一级、二级监控指标需分别满足式(1)和式(2)。

式中:δ为大坝变形;[δI]为大坝变形一级监控指标;[δII]为大坝变形二级监控指标;K为整体刚度矩阵;δH、δT、δθ分别为水压、温度和时效引起的位移矩阵;RH、RT、Rθ分别为水压、温度和时效引起的荷载列向量;E、μ、c、φ分别为混凝土或基岩弹性模量、泊松比、凝聚力和内摩擦角;Kf和[Kf]分别为抗滑稳定安全系数和抗滑稳定允许安全系数;Kσ和KC分别为裂缝尖端应力强度因子和断裂韧度;εve和εvp分别为黏弹性变形和黏塑性变形;B和D分别为几何矩阵和弹性矩阵。
2.2 混凝土坝变形监控指标拟定混合计算方法由于混凝土坝变形监控指标拟定十分复杂,涉及的坝体和基岩的弹性参数、强度参数和黏性参数众多且不容易准确获取[16-17]。考虑到水压分量数值计算涉及的参数相对较少且计算结果相对可靠,为此,采用基于数值计算-变形统计模型的混合法拟定混凝土坝变形监控指标,即水压分量由数值计算分析法计算获得,不利工况下的温度分量和时效分量,则由长时间系列混凝土坝变形监测资料统计模型分离获得,从而叠加得到混凝土坝变形一级、二级监控指标:

式(4)中各不利工况下的水压、温度和时效分量的具体计算如下:
(1)最不利水压分量。一级监控指标通过参数反演获得坝体混凝土和基岩的等效弹性参数,输入大坝有限元计算模型,计算给定不利水位工况下的水压分量差,作为大坝变形一级监控指标的水压分量差;二级监控指标考虑坝体混凝土和基岩的塑性屈服,凝聚力和内摩擦角等强度参数采用设计值,其由强度参数极限值或标准值除以折减系数得到,坝体混凝土和基岩的弹性参数仍采用反演值,建立弹塑性大坝有限元模型,计算不利水位工况下的水压分量差,计算结果作为大坝变形二级监控指标的水压分量差。
(2)最不利温度分量。一级监控指标由变形统计模型分离出的温度分量,计算得到温度分量向下游的最大位移,进而得到不利温度工况下相对起始日的一级监控指标温度分量差;二级监控指标由于变形统计模型分离出的温度分量本质上为线性温度分量,而一些极端不利温度工况下会产生非线性的温度效应[18],为此,由不利温度工况下的实测变形扣除变形统计模型分离出的水压分量和时效分量,进而得到含非线性因素的真实温度分量,在非线性温度分量基础上,选取相对于起始日真实温度分量向下游最大的差值作为二级监控指标的温度分量差。
(3)最不利时效分量。由变形统计模型分离出时效分量,选取至起始日起,时效分量最大变幅值(最大值-最小值)作为一级和二级监控指标的时效分量差[2,10]。
3 应用实例
3.1 工程概况新疆某常态混凝土双曲拱坝坝顶高程649.00 m,建基面高程555.00 m,最大坝高94.00 m,坝顶厚10 m,坝底厚27 m,坝顶弧长319.646 m。正常蓄水位为646.00 m,设计洪水位643.73 m,校核洪水位647.21 m。大坝河床岩基主要为中泥盆纪阿勒泰组厚层—巨厚层状灰白色花岗片麻岩,微风化~新鲜岩体质量属AⅡ类岩体;两岸为厚层—巨厚层状灰白色花岗片麻岩,局部为薄层—中厚状灰黑色黑云母斜长片麻岩,微风化~新鲜岩体质量属AⅡ、BⅢ类。其水平位移主要由正倒垂线组进行监测,布置如图1所示,选择坝顶处3个测点PL 1-3、PL 2-3、PL 3-3,采用数值计算-变形统计模型的混合法进行大坝变形监控指标拟定。

图1 拱坝正、倒垂线监测布置图
3.2 拱坝变形统计模型建立由变形监测资料定性分析可知,该拱坝径向水平位移主要受水压、温度和时效等因素的影响,由此,建立大坝径向水平位移监测资料统计模型为[1,19]:

式中:Hi为观测日当天上游水深的i次方;Hi0为建模资料序列第一个观测日当天上游水深的i次方;a1、a2、a3、a4为上游水深分量的回归系数;t为观测日至始测日的累计天数;t0为建模资料序列第一个观测日至始测日的累计天数;b1、b2、b3、b4为温度分量的回归系数;θ为观测日至始测日的累计天数t除以100;t0为建模资料序列第一个观测日至始测日的累计天数t0除以100;c1、c2、c3为时效分量的回归系数。
结合坝顶处测点PL 1-3、PL 2-3、PL 3-3的水平径向位移监测资料系列(2016年10月2日—2020年10月29日),采用逐步回归分析法对式(5)进行回归分析,3个测点回归分析的复相关系数分别为0.935、0.878和0.967,这说明本文建立的变形统计模型效果良好。3个测点实测值和统计模型拟合值对比如图2所示。
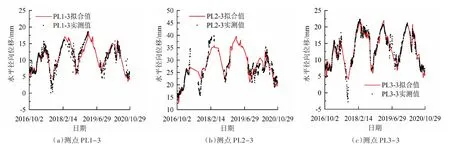
图2 大坝坝顶处典型测点实测值与统计模型拟合值对比
3.3 坝体和基岩弹性模量优化反演采用正交设计-BP神经网络-数值计算[20]相结合的方法进行坝体混凝土和基岩弹性模量反演。主要计算过程如下:
(1)大坝三维有限元模型建立。依据该大坝设计报告及坝基地质资料,向上下游、左右岸和地基深度各截取1~2倍坝高范围,建立三维有限元计算模型。三维有限元模型坐标系x向为顺河向,以指向上游为正,y向为横河向,以指向右岸为正,z向为垂直向,以向上为正,反之为负。采用六面体八节点等参单元进行网格剖分,共剖分单元数为35 589,节点数为42 843,其中,坝体单元数为19 645,节点数为24 315。将坝体以及坝基概化为三种材料,其中,坝体混凝土概化为一种材料,坝基花岗片麻岩(D2a-4)概化为一种材料(基岩类型I),坝基黑云母斜长片麻岩(D2a-3和D2a-5)概化为一种材料(基岩类型II)。拱坝三维有限元模型以及模型材料概化分区见图3。

图3 拱坝三维整体有限元模型
(2)反演参数取值范围确定。根据设计报告以及工程地质勘察报告确定拱坝各分区材料弹性模量参考值,根据工程经验,确定各分区材料弹性模量取值范围[21],如表1所示。

表1 材料弹性模量取值范围
(3)计算工况选取。根据实测水位资料,该坝在2019年12月27日至2020年4月14日期间,库水位变化较大,水位由644.3 m降低到628.2 m,为此,选取上游水位H1=644.3 m和H2=628.2 m作为计算工况水位。
(4)反演样本获取。结合表1的参数取值范围,采用3因素5水平的正交设计表(L25(53)),得到3种材料的25种参数组合,将其逐一代入建立的大坝有限元计算模型中,得到计算工况水位对应的水平位移水压分量差。为了和正倒垂线实测位移进行对比,将直角坐标系下的计算位移通过位移转换得到径向位移,由此获得反演学习样本如表2所示。

表2 材料参数反演学习样本
根据表2,将水平位移差计算值作为输入,对应样本E1、E2、E3的弹性模量作为输出,采用BP人工神经网络建立变形水压分量差与弹性模量之间的非线性映射关系。
(5)反演结果及验证。根据式(5)建立的变形统计模型分离得到对应水位H1与H2下各典型测点的水压分量差值,将其输入到训练好的神经网络模型中得到弹性模量反演值,其中坝体混凝土(E1)弹性模量为32.49 GPa,基岩类型I(E2)弹性模量为18.03 GPa,基岩类型Ⅱ(E3)弹性模量为14.90 GPa。将反演弹性模量对应输入大坝三维有限元模型中,计算出水位H1和H2工况下拱坝计算变形的差值,并与实测位移分离出来的水压分量差进行对比验证,验证结果见表3。

表3 反演结果验证
由表3结果可知,实测水压分量差与计算位移差相差较小,说明本次反演结果是有效的。
3.4 大坝变形监控指标拟定
(1)变形一级监控指标拟定。由该拱坝径向水平位移和环境量(库水位和日平均气温如图4所示)的相关性分析可知,坝顶处测点PL1-3、PL2-3、PL3-3的水平径向位移主要表现为向下游位移(如图2所示,黑色线表示库水位,红色线表示日平均气温);库水位较高时,大坝向下游变形较大;低温季节时,温度引起的向下游变形也较大,即高水位低温对大坝变形不利。为此,在拟定该坝变形一级监控指标时,选取低温高水位作为计算工况。

图4 库水位和日平均气温过程线
水压分量计算。该拱坝自下闸蓄水运行以来,在2017年10月27日出现历史最高水位646.20 m,超过了正常蓄水位646.00 m,为此,选择历史最高水位646.20 m作为不利计算水位工况;通过分析该拱坝径向水平位移和库水位监测资料,选择较低水位630.54 m的2017年3月27日作为起始日。结合3.3节优化反演的材料参数,将选定的水位输入所建立的大坝三维有限元计算模型,通过线弹性有限元计算得到不利工况下的水压分量差。
温度分量选取。由3.2节建立的变形统计模型,分离出温度分量,计算得到相对于起始日向下游最大的差值作为对应温度分量的差值。
时效分量选取。由3.2节建立的变形统计模型,分离出时效分量,选取至起始日起的最大变幅值作为最不利时效分量差。
变形一级监控指标拟定结果。根据式(4)得到该坝变形一级监控指标,如表4所示。

表4 大坝变形一级监控指标拟定结果
(2)变形二级监控指标拟定。水压分量计算与变形一级监控指标类似,选择历史最高水位646.20 m作为不利计算水位工况,并选择较低水位630.54 m的日期作为起始日。假设坝体混凝土和基岩的屈服准则满足Drucker-Prager屈服准则,强度参数采用设计值,由凝聚力和摩擦系数建议值除以折减系数获得。混凝土重力坝设计规范(SL319-2018)基于单一安全系数法进行设计,坝体混凝土抗压安全系数,基本组合不应小于4.0;特殊组合(不含地震)不应小于3.5;混凝土拱坝设计规范(SL282-2018)基于单一安全系数法进行设计,对于基本荷载组合,1级、2级拱坝的安全系数采用4.0,3级拱坝的安全系数采用3.5。非地震情况特殊荷载组合,1级、2级拱坝的安全系数采用3.5,3级拱坝的安全系数采用3.0。由于单一安全系数法将工程中各种不确定性用一个安全系数来表征,虽然简单,但只是定性的标准,没有定量的意义,而分项系数法更加的定量和科学,为此,本文根据混凝土重力坝设计规范(NB/T 35026—2014),选择分项系数法中的材料性能分项系数来获得设计强度值,凝聚力和摩擦系数对应的折减系数分别为2.0和1.7。依据该大坝设计报告及坝基地质资料,坝体混凝土、基岩类型Ⅰ和基岩类型Ⅱ相应的凝聚力建议值分别为2.50 MPa、1.10 MPa和0.95 MPa,摩擦系数建议值分别为1.428、1.2和1.1,容易得到强度参数相应的设计值,进而由内切圆公式计算得到Drucker-Prager屈服函数对应的材料参数α和K[11],然后通过弹塑性有限元计算获得不利工况下水压分量差。
温度分量选取。由该拱坝径向水平位移和环境量(库水位和日平均气温)的相关性进一步分析可知,该坝除了高水位低温工况下会引起较大的向下游变形,另外,该坝在运行过程中会遭遇低水位与极端低温同时发生工况。此时大坝上游面混凝土裸露面积增大,由此引起的温度分量相对于高水位低温工况下的温度分量更为不利。为此,考虑到低水位低温工况会引起的复杂的不利变形效应量,根据实测径向位移和变形统计模型的水压分量和时效分量分离出低水位低温工况下的实测温度分量:


图5 非线性温度分量与线性温度分量过程线对比
由于该实测温度分量差值包含了不利温度工况引起的非线性温度分量,取其最大差值作为变形二级监控指标的温度分量差。
时效分量选取。由3.2节建立的变形统计模型,分离出时效分量,选取至起始日起的最大变幅值作为最不利时效分量差。
变形二级监控指标拟定结果。根据式(4)得到该坝变形二级监控指标,如表5所示。

表5 大坝变形二级监控指标拟定结果
(3)变形监控指标拟定结果评价。作为对比,结合实测变形监测资料系列,选取测点每季度向下游最大位移组成典型效应量集合,采用典型效应量小概率法[5]拟定坝顶处测点PL1-3、PL2-3、PL3-3的水平径向位移监控指标,其特征值如表6所示。

表6 典型效应量特征值
将表6中的特征值代入式(7)计算监控指标。

对比混合法与典型效应量小概率法拟定结果,如表7所示。由表7可知,三种监控指标均大于历史最大监测值;由于典型小概率法拟定的监控指标为大坝处在正常工作状态下的监控指标,混合法拟定的变形一级监控指标与该值接近但略大,其原因为混合法拟定的变形一级监控指标考虑的因素更全面。这同时也表明,该拱坝目前处于黏弹性工作性态。

表7 大坝变形一级、二级监控指标拟定结果对比
4 结论
本文采用数值计算-变形统计模型的混合法拟定混凝土坝变形监控指标,并结合某常态混凝土高拱坝,展示了基于混合法的混凝土坝变形一级、二级监控指标拟定。通过分析得到如下结论:
(1)给出了基于数值计算-变形统计模型的混合法拟定混凝土坝变形一级、二级监控指标的计算准则,以及给出了不利工况下水压分量、温度分量和时效分量的计算方法;其中在计算变形二级监控指标的水压分量时,引入凝聚力和摩擦系数对应的材料性能分项系数来获得强度参数的设计值;在计算变形二级监控指标的温度分量时,采用包含了非线性温度分量的不利温度工况下的实测温度分量差。
(2)结合某常态混凝土高拱坝拟定变形监控指标结果表明,基于混合法拟定的变形一级监控指标与典型小概率法拟定的变形监控指标接近但略大,这表明该拱坝目前处于黏弹性工作性态,而且混合法拟定的变形一级监控指标考虑的因素更全面。

