四阶张量分解在视频压缩领域的应用

徐娇娇， 杨志霞， 姚 瑞

(1. 昌吉学院 数学系， 新疆 昌吉 831100； 2. 新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046；3.新疆师范大学 数学科学学院， 新疆 乌鲁木齐 830000)

0 引言

以四阶张量为主要展现形式的数据广泛存在于各种实际问题中，例如不同患者在不同药物剂量下的EGG数据、各种视频数据、单镜头的人脸识别问题等.尤其视频数据作为四阶张量的表现形式，引起了广大学者的注意，如视频压缩[1]、视频恢复[2]、视频分类[3]等.数字图像压缩技术在多媒体、通信、医学等诸多领域有着广泛的应用.我们知道，奇异值分解(SVD)[4]和非负矩阵分解[5]在图像压缩理论中非常重要.与灰度图像相比，彩色图像和视频具有更多的信息和识别特征，对彩色图像和视频进行处理，具有广泛的潜在应用.目前存在很多数据描述方法[6]，使用向量或矩阵存储彩色图像和视频数据信息、压缩或处理数据时，不仅占用了大量的存储容量，而且破坏了数据的原始结构信息.因此，彩色图像和视频被表示为多维数组，多维数组通常称为高阶张量.以高阶张量的形式保存彩色图像，可更多保护数据的原始结构.因此，使用张量存储更复杂的数据也更加合理.

事实上，张量可以看作是矩阵的推广，关于张量的研究方向有很多，如张量逼近[7-9]、张量完备[10-13]、张量特征值问题[14-15]、支持张量机[16]以及张量分解等问题.特别是张量分解问题广受关注.现有的张量分解包括Tucker分解[17-18]、高阶奇异值分解(HOSVD)[19]、CANDECOMP/PARAFAC(CP)分解[20]、张量稀疏分解[21]等.Tucker分解通常表示为向量的外积之和，它也可以表述为张量模乘[22].特别地，高阶奇异值分解具有与Tucker分解相同的结构形式，可以看作是矩阵奇异值分解的拓展.类似于Tucker分解，CP分解被定义为向量的外积之和.另一个重要的分解是对称张量的低秩分解[23].此外，文献[24]还构建了一个新颖的多线性张量空间.具体地，不仅给出了任意多维离散变换，而且给出了矩阵空间上的四阶张量双线性算子；还定义了四阶张量的L-奇异值分解和张量L-QR分解.它们都具有精度高、收敛速度快、计算量小的特点.值得注意的是，Kilmer等[25]和Golub等[26]通过块循环矩阵和展开算子定义了两个三阶张量之间的乘法运算.在此基础上，对块循环矩阵进行离散傅里叶变换(DFT)，得到T-奇异值分解.由于矩阵可视为张量，因此矩阵的T-奇异值分解与矩阵奇异值分解一致.可见该三阶张量的分解算法不仅具有很好的稀疏性，而且具有很好的保结构性.因此，将其推广到四阶张量是一个亟待解决的问题.

另一方面，彩色视频可视为四阶张量，其维数高于三阶张量.因此，研究四阶张量的分解具有重要意义.为了节省计算资源和保持数据结构，可以通过截断的方法在保持原数据特征不变的前提下，压缩四阶张量的数据量.然而，由于维度增加，四阶张量的数据结构比三阶张量更复杂.此外，四阶张量的研究相对少于三阶张量，包括乘法和分解.我们探索了一种新的四阶张量分解以及截断的四阶压缩算法.

本文主要研究四阶张量分解在视频压缩领域的应用.首先，研究了块循环三阶张量和离散傅里叶变换，定义了四阶张量之间的乘法.基于以上定义，提出了一个新的四阶张量分解及其算法.具体地，原始的四阶张量被分解为两个T-正交张量和一个对角张量的乘法.经过适当的截断，压缩了原始四阶张量的存储量.通过数值实验表明了本文提出的四阶张量分解算法的有效性和可行性.

本文安排如下：第一节，描述了一些符号，并回顾了一些张量背景知识；第二节，定义了两个四阶张量的乘法，并基于块循环三阶张量的离散傅里叶变换提出了四阶张量分解；第三节，分别通过随机数据和真实照片数据进行数值实验，验证了本文提出的张量分解和视频压缩算法的有效性；最后，总结了本文的主要结论.

1 符号和张量背景

在本文中，我们用大写手写体字母表示张量(例如：X)，用大写字母表示矩阵(例如：A)，而黑体小写字母和小写字母分别表示向量和标量.

一个N阶张量是具有N个向量空间的张量积空间中的一个元素，即一个N维数组

X=(xi1,i2,…,in)∈Rd1×d2×…×dN，

其中“×”表示笛卡尔积，dn表示张量X第n维的大小.特别地，向量是一阶张量，矩阵是二阶张量.当一个张量的阶数不小于3时，称其为高阶张量，若N=3，则X称为3阶张量，若N=4，则X称为4阶张量.

下面，先介绍循环矩阵的定义.给定向量v=(v0v1v2v3)T∈R4，称矩阵

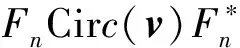
若三阶张量中的每一个前后矩阵片由循环矩阵代替，可得三阶张量的块循环矩阵，下面以1-模展开块循环矩阵为例，具体定义如下：

定义1.1(循环三阶张量)形式为

的三阶张量C，称为循环三阶张量，其中ci为循环矩阵中的一个元素.

为了方便后文引入四阶张量的离散傅里叶变换，这里首先给出两个与三阶张量相关的定义.

定义1.2(Face-wise乘积[27])设三阶张量X∈Rd1×d2×d3， Y∈Rd2×m×d3.那么X和Y的Face-wise乘积定义为

X*Y=

(X(1)Y(1)|X(2)Y(2)|…|X(d3)Y(d3))，

其中X(i)和Y(i)(i=1,2,…,d3)分别表示X和Y的前后矩阵片.

定义1.3(Kronecker积)设矩阵X∈RI1×I2，张量Y∈RJ1×J2×J3，则X和Y的Kronecker积定义为

X⊗Y=(Yj1,j2,j3⊗X)，∀jm∈Jm，m=1,2,3,

其中

X⊗Y∈R(I1J1)×(I2J2)×J3.

显然，当三阶张量降阶为二阶张量(矩阵)，张量的Kronecker积即为矩阵的Kronecker积.

2 四阶张量乘法及其分解

本节，我们首先提出四阶张量的1-模展开和折叠算子.接下来，给出块循环的三阶张量与其相应的离散傅里叶变换.随后，定义两个四阶张量间的乘法和一些特殊的四阶张量乘法.最后，建立一种新的四阶张量分解方法，并提出相应的算法.

2.1 四阶张量算子

本小节，依次介绍四阶张量的Frobenious范数、1-模展开算子以及1-模折叠算子的定义.为了叙述方便，本文主要讨论四阶实张量.若向量空间V1、V2、V3、V4的维数分别是d1、d2、d3、d4，则张量积空间V1∘V2∘V3∘V4中任意一个四阶张量X表示为

其中

v1i∘v2j∘v3k∘v4k(1≤i≤d1,1≤j≤d2,

1≤k≤d3,1≤l≤d4)

是张量积空间V1∘V2∘V3∘V4的一组基.对于四阶张量X=[|xi,j,k,l|]∈Rd1×d2×d3×d4，其Frobenious-范数定义为

对于张量X∈Rd1×d2×d3×d4，X的1-模展开算子为

(·)〈1〉∶Rd1×d2×d3×d4→R(d1d4)×d2×d3

X→X〈1〉.

折叠算子记作(·)〈1〉，定义为

(·)〈1〉∶R(d1d4)×d2×d3→Rd1×d2×d3×d4

X〈1〉→X.

类似地，也可以定义n-模(n=2,3,4)展开及其折叠算子.

利用上述描述，我们得到下面的定义．

定义2.1(四阶张量的1-模展开)给定四阶张量X={xi,j,k,l}∈Rd1×d2×d3×d4，若按照X的1-模的方向排列其每一个子三阶张量，则得到X的1-模展开三阶张量

其中X(1)=X(:,:,:,l)∈Rd1×d2×d3(l=1,2,…,d4) 是第l个1-模展开子三阶张量.类似地，也可以定义n-模(n=2,3,4)展开和折叠算子.

2.2 块循环三阶张量和离散傅里叶变换

有了上述循环三阶张量的定义，下面我们给出块循环三阶张量的定义.

定义2.2(四阶张量的块循环三阶张量)对于四阶张量X∈Rd1×d2×d3×d4，X(j)(j=1,2,…,d4) 是张量X的1-模展开三阶张量X〈1〉的第j个三阶子张量，把形式为

∈Rd1d4×d2d4×d3d4

的三阶张量称为四阶张量X的块循环三阶张量，记为Circ(X).

下面，以四阶张量X∈Rd1×d2×d3×3为例，给出其块循环三阶张量(见图1).

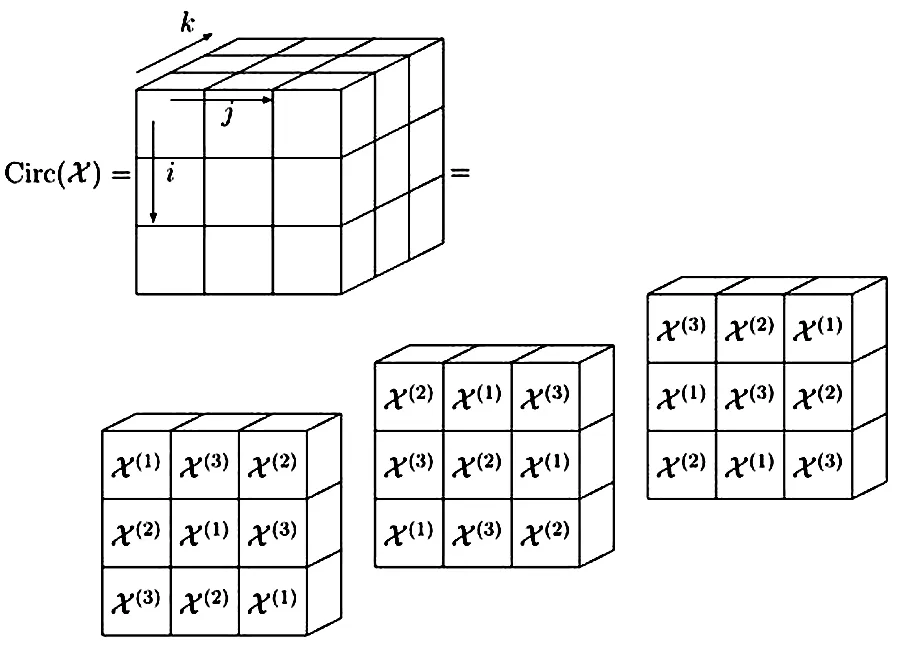
图1 四阶张量X∈Rd1×d2×d3×3的块循环三阶张量

换个角度，Circ(X)可以看作d4个维数为d1d4×d2d4×d3的块三阶张量的排列.进一步，通过张量的3-模展开，块循环三阶张量Circ(X)的每一个三阶子张量都可转化为矩阵.也就是将维数为d1d4×d2d4×d3d4的块循环张量Circ(X)转化为一个维数d1d4×d2d3d4×d4的三阶张量，记作TenMat(X)，即

我们知道，利用离散傅里叶变换，循环矩阵能够被对角化.类似地，下面给出块循环三阶张量的块对角化过程.给定四阶张量X∈Rd1×d2×d3×d4离散傅里叶矩阵Fd1∈Rd1×d1，则有

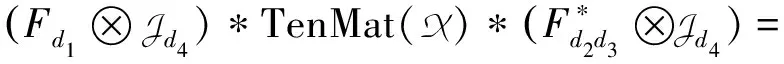
其中Jd4∈Rd4×d4×d4为对角线元素全为1的三阶张量，*表示两个三阶张量的Face-wise乘.值得注意的是，每个矩阵Dl∈Rd1×d2d3(l=1,2,…,d4) 应该是稠密的.相反地，通过离散傅里叶逆变换，TenMat(X)能够被计算出来，即

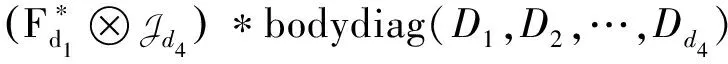
特别地，上述两个过程分别记作fft{TenMat(X)}和ifft{TenMat(X)}.

2.3 张量乘法

在本小节，我们给出四阶张量的乘法，这也是本文的主要贡献之一.下面，主要给出一个新的四阶张量乘法的相关定义和张量模乘的定义.此外，还定义了一些特殊的四阶张量.

定义2.3(B-乘)对于四阶张量X∈Rd1×d2×d3×d4和Y∈Rn1×n2×n3×n4，且d2d3=n1n4，四阶张量的B-乘为

X*BY=(X〈1〉〈3〉Y〈1〉〈3〉)〈1〉〈3〉∈Rd1×n2×n3×d4，

其中X〈1〉〈3〉是X〈1〉的3-模展开矩阵，·〈1〉〈3〉是折叠算子.

容易看出，四阶张量的B-乘基于展开矩阵X〈1〉〈3〉和Y〈1〉〈3〉之间的乘法.下面，给出张量B-乘与张量模乘之间的关系.

命题1对于张量B-乘，矩阵A∈Rn1×n2能够视为一个四阶张量，且n3=n4=1.此时，定义2.3退化为矩阵乘法.进一步，设四阶张量X∈Rd1×d2×d3×d4，矩阵A∈Rn1×n2且d2d3=n1,则

X*BA=X〈3〉×2AT∈Rd1×n2×d4，

其中×n表示张量和矩阵之间的n-模乘法.

证明已知四阶张量X的3-模展开张量为X〈3〉，其第k个前后片为d1×d2d3的矩阵X(k)(k=1,2,…,d4).由张量的B-乘的定义知，张量X与矩阵A的B-乘，即为三阶张量X〈3〉的每个前后片与矩阵A=(amn)n1×n2相乘.

具体如下：

进一步，有

另一方面

因此，通过2-模乘法的定义，命题1成立.

现在，提出几个具体的四阶张量相关的定义.基于四阶张量B-乘，给出四阶Tb-正交张量的定义.

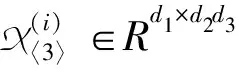
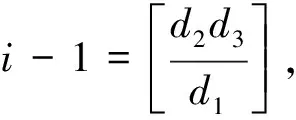
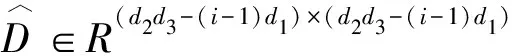
下面，将给出Tb-正交张量、单位张量以及张量的Tb-转置的定义.

定义2.5(单位张量)若四阶张量J∈Rd1×d1×d3×d4的第i(i=1,2,…,d4)个子三阶张量的第i个前后片是一个d1×d1的单位矩阵,则称F为四阶单位张量.

定义2.6(Tb转置)设四阶张量X∈Rd1×d2×d3×d4，其Tb转置定义为

XTb=((X〈1〉〈3〉)T)〈1〉〈3〉∈Rd2×d1×d4×d3，

其中，X〈1〉〈3〉∈Rd2d3×d1d4表示X的展开矩阵.

有了四阶单位张量和张量的Tb转置的定义，下面给出四阶Tb-正交张量的定义.

定义2.7(Tb-正交张量)四阶张量Q∈Rd1×d2×d3×d4称作Tb-正交张量，如果

Q*BQTb=J，

其中J∈Rd1×d1×d4×d4是单位张量.

注释1：我们知道正交矩阵和三阶正交张量都能确保Frobenius范数不变性.本文定义的Tb-正交张量也具有保范性，也就是说，如果Q∈Rd1×d2×d3×d4是Tb-正交张量，且X∈Rn1×n2×n3×n4满足d2d3=n1n4，则 ‖Q*BX‖F=‖X*BQ‖F=‖X‖F.

2.4 四阶张量分解

本小节，基于四阶张量B-乘，我们提出一个新的四阶张量分解方法.当四阶张量退化为矩阵时, 该分解即为矩阵的奇异值分解.同时本小节也给出对应的算法.

定理1(B-TD)设四阶张量X∈Rd1×d2×d3×d4，X的奇异值分解为

X=U*BS*BVTb，

其中U∈Rd1×d1×d4×d4，V∈Rd2×d2×d3×d3是Tb-正交张量， S∈Rd1×d2×d3×d4是对角张量.四阶张量的奇异值分解简记为B-TD.

证明首先，对TenMat(X)做离散傅里叶变换.也就是说，存在两个傅里叶矩阵Fd1∈Rd1×d1和Fd2d3∈Rd2d3×d2d3使得

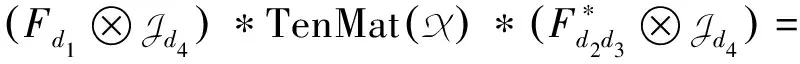
其中Di∈Rd1×d2d3，i=1,2,…,d4.

接下来，将上式中所有的稠密矩阵排列成一个三阶张量，即

D=(D1|D2|…|Dd4)∈Rd1×d2d3×d4.

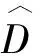
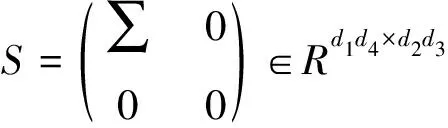
也就是说

令

且i,j=1,2,…,d4，有

其中k=1,2,…,d4.进而有

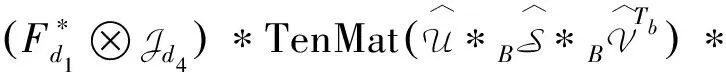
因此，有

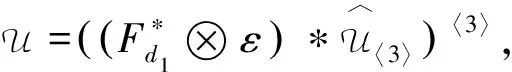
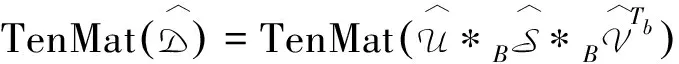
这意味着X=U*BS*BVTb.显然， U、V均是Tb-正交张量,且S是对角张量.

注释2：值得一提的是，对于四阶张量X∈Rd1×d2×d3×d4，当d3=d4=1时，分解式X=U*BS*BVTb退化为矩阵的奇异值分解.此时，U和V是正交矩阵，S是对角矩阵.

为了获得四阶张量X∈Rd1×d2×d3×d4的奇异值分解，根据定理1的证明过程可总结出如下算法：

算法1四阶张量分解(B-TD)

输入：X∈Rd1×d2×d3×d4

输出：U，S，V

bodydiag(D1,D2,…,Dd4)=fft(TenMat(X))

D=(D1|D2|…|Dd4)

3 数值实验

本节，通过两个数值试验来验证本文提出的四阶张量的奇异值分解算法(B-TD)的可行性.第一部分数值算例，将本文四阶张量的奇异值算法应用在一个人造数据中，验证了本文提出的算法不仅是可行的，同时也具有较高的计算精度.第二部分数值算例是针对实际的视频数据，执行了本文所提的算法，通过不同的压缩比对视频数据进行不同的压缩效果，从而表明了本文所提算法的实用性.

3.1 人造数据

算例1本例中，X是由Matlab随机产生的维数为3×3×3×3的四阶张量，下面通过三个三阶子张量拼接的形式，将四阶张量X中展示如下：

X=(X(1)|X(2)|X(3))∈R3×3×3×3.

这里具体给出三个三阶子张量.

通过我们的B-TD算法，得到张量S=(S(1)|S(2)|S(3))，其三阶子张量分别为

显然S是对角张量.类似地，同样能够计算出Tb正交张量U和V，这里不再一一列举.除此之外，我们也能计算原始张量X与分解后的张量之间的误差，即

‖X-U*BS*BVTb‖F=3.9146e-14.

上述误差表明，B-TD算法具有较高的误差精度，也表明了方法的可行性.

3.2 图像压缩应用

我们知道，实际的计算机视频处理问题中，关键技术是海量数据的表示和传输.因此，如何有效地存储和传输视频数据成为信息社会迫切需要解决的问题.视频数据压缩的原理是将稠密的视频数据转换成具有相同特征的稀疏数据.

实际数据中的彩色图片是三阶张量，无声的视频是以时间为第四个维度的四阶张量.为了清晰地显示数据压缩的结果，我们将本章提出的新的四阶张量分解理论应用于视频数据.具体地，将B-TD方法应用在图像压缩问题上.考虑到这些照片的质量随曝光时间、光线和视点的不同而变化.因此，首先考虑将已有的图像数据做归一化处理.具体做法如下：

Pl(l=1,2,…,d4)是一个d1×d2×d3维的三阶张量.Pl是由d3个d1×d2的矩阵片构成，其中每个矩阵片表示第l个人的一张人脸图像.做归一化处理，即每个Pl减去其均值.把处理过后的张量记作X(:,:,:,l)，即X(:,:,:,l)=Pl-Ψ，其中

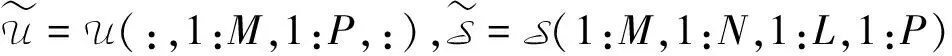
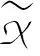
算法2视频压缩算法(TDVC)

输入：实验数据Pl(l=1,2,…,d4)，截断参数M，N，L，P

对图像做归一化处理，Ψ；

forl=1,2,…,d4X(:,:,:,l)=Pl-Ψ；

End

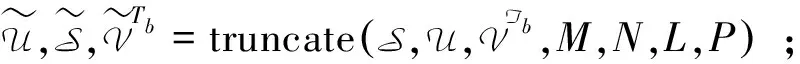
下面给出用来衡量压缩效果的视频压缩率的计算方法.X∈Rd1×d2×d3×d4表示原始的视频压缩数据.可以看出X具有d1d2d3d4个像素.利用算法2对X进行截断，截断后的数据像素为d1MPd4+NL+Nd2d3L.数据压缩率定义为截断前的像素值与截断后的像素值的比值，即

显然，大的压缩比可以大大节省数据的存储空间.此外，图像的视觉效果也是很重要的.基于此，下面给出一个基于不同视频压缩比的例子.

a原始图像 b M=40,N=30 c M=20,N=20 d M=10,N=10 ρ=4.2637 ρ=7.5641 ρ=15.1282图2 原始图像与对应于不同的截断参数和压缩比的重构图像对比

a原始图像 b M=100,N=100 c M=40,N=20 d M=10,N=10 ρ=5.1404 ρ=14.9938 ρ=51.4041图3 原始图像与对应于不同的截断参数和压缩比的重构图像对比

通过原始图像与选择不同的截断参数M，N，L，P得到后面三列不同的重构图像.可以发现，L和P的值并不影响压缩后照片的清晰度，故上述过程取L=P=1.该方法不仅可以压缩数据的存储量，而且保留了原始数据的主要特征.由此表明本文的分解方法不仅可节省计算时间，而且减少图像的存储空间.

算例3本例中，我们从AbsFreepic网站下载了三张彩色照片.每张彩色照片大小为Pl∈R300×400×3(l=1,2,3)，利用算法2TDVC分解四阶张量P∈R300×400×3×3，效果如图3所示.

图3中，最左侧第1列为原始图像，其他三列是在不同的压缩比下，由算法2 TDVC压缩后的图像.同样地，设L=P=1，不难看出重构的图像同样保存了原始数据的主要特征，且N和M的值越大，重构的图片的清晰度越高.

4 总结

本文提出了一个新的四阶张量乘法和四阶张量奇异值分解算法(B-TD)，该方法具有很好的稀疏性和保范性.我们将所提算法应用到视频压缩领域，通过选取不同的截断参数，计算视频数据的压缩比，以成组的黑白照片、彩色照片构造成四阶张量进行分解.压缩后的视频数据表明，不同的压缩比会得到清晰度不同的视觉效果. 数值实验能很好地说明本文提出的四阶张量分解方法的可行性.在后期的研究工作中，我们将继续以高阶张量分解为研究课题，进一步探讨更多的应用领域.