基于Softplus函数的神经网络的Reluplex算法验证研究

陆明远 侯春燕 王劲松

(天津理工大学计算机科学与工程学院 天津 300384)

(1933044495@qq.com)

形式化验证是通过数学方法证明一个系统没有漏洞且实现了设计者的规划，在软硬件检测中都有较多应用.人工神经网络则在人工智能领域和相关的工业生产中不可或缺.既然要了解一个神经网络系统的综合性能并评价和检验其自我学习的效果，就必须采用合适方式来验证神经网络，可以充分地运用形式化验证的方法来进行指导和辅助[1-2].在进行神经网络验证方面的研究时，通过对深度神经网络选择不同的激活函数进行测试和比较研究，能更好地了解神经网络的鲁棒性、感知能力和深度学习能力[3]，并对比分析不同激活函数的适用性，从而更有利于对神经网络深度学习的总体研究[4].

1 研究现状

近年来形式化验证的实践方法在不断发展，其应用层面涉及到测验IEEE标准、客户端与服务端传输数据校验、程序稳定性等.形式化验证的相关应用软件也逐渐成为各大厂商愿意进行商业投资的方向之一[5-6].

数十年来在仿照高等动物的神经网络系统对信息进行反馈功能的机制下[7]，人工神经网络已能高效完成许多看似艰巨的任务计划[8]，其结构框架也在愈发复杂深邃化，解决工业、服务业和学术研究方面的能力普遍增强[9].而Reluplex作为针对神经网络错误进行检验校对的算法，充分运用了形式化验证技术与可满足性模理论(SMT)的方法，可以采用具体的输入数据充分验证各个神经网络的特性，对研究和优化神经网络的深度学习能力有很大帮助[10-11].

2 Reluplex算法简介

单纯形算法(Simplex)是迭代算法的1个子类型，该算法一般先尝试假设出1个最初的解集并进行代入测试，随后分析出这个解集是否为问题的最优解.如果不是，就在目前已有解的基础上通过约束条件优化得到1组更合适的解集，于是不断地迭代更替下去，目标参数越来越接近于期望值.Reluplex算法则将Simplex应用于深度神经网络验证领域，它擅长于验证无人机是否会发生碰撞的安全性事故[10].Reluplex允许互为决定的非基本变量Xb，Xf暂时不符合逻辑关系，以Update操作与迭代操作纠偏之前的取值范围与等式关系[10]，这是其之于Simplex的改进.

(1)

(2)

(3)

(4)

(5)

下标b和i表示输入，f和j表示输出，l表示下限.在Reluplex的5点基本操作中，Updateb与Updatef均是给非基本变量重新赋值，以纠正其之前的数值超出取值范围的错误，导致式子左边的基本变量超出取值范围，就要采用PivotForRelu操作来迭代，将其移到右边与非基本变量相互易位，若引起方程组内别的式子里的基本变量也超出取值范围，便继续迭代，最终方程组内任何式子都符合各个限制规则.ReluSplit操作采取拆分的方式判定lower(Xi)=0与upper(Xi)=0时Relu分别为激活状态与未激活状态.ReluSuccess操作则设定Xb与Xf在逻辑上的相互关系，若Xb>0，则将Xf调整成等同于Xb；若Xb≤0，Xf则调整成0[10]，所有变量最终都要符合约束条件.而Relu激活函数在深度学习算法中相对较为常见[12-13]，它在输入的数值为负数时，始终保持对外输出数值0；而在输入的数值为正数时，输出则保持与其输入量一致.

Relu激活函数(如图1所示)为

图1 Relu激活函数图像

3 算法设计

3.1 理论分析

Relu激活函数也有着自身的局限性.由于它在负半轴上的斜率始终为0并保持输出0，这使得它在具体的环境下很容易变成“垂死的Relu”，从而在训练深度神经网络的过程中表现得非常脆弱[14].在这种情况下，需要对Relu激活函数进行改进，将其替换成其他与之类似的激活函数进行测试，进行相应的比较研究，从而能更好地了解深度神经网络的安全性和不同激活函数的适用性[15].将Reluplex算法中所运用的Relu函数更换成比其更平滑的Softplus函数，可以改良其算法的实现效果[16].可以将Softplus视为比ReLu更平滑的近似替代品，根据神经科学家的相关研究，Softplus比Relu更加接近脑神经元的激活模型[17-18].

Softplus函数(如图2所示)为

f(x)=ln(1+ex).

图2 Softplus的函数图像

Softplus的导函数(如图3所示)则为

图3 Softplus的导函数图像

如图4所示，当x较小时，Softplus的斜率接近于0，比Relu函数要平滑得多，随着x的逐渐增大，Softplus的导函数越来越无限接近于1，从而逐渐与Relu函数趋同起来.

图4 Relu激活函数和Softplus激活函数的对比

Updateb1=(Xi∉B,(Xi,Xj)∈,α(Xj)≠

(αupdate(α,Xi,α(Xj)-α(Xi))).

(6)

Updateb2=(Xi∉B,(Xi,Xj)∈,α(Xj)≠

(αupdate(α,Xi,()·α(Xj)-α(Xi))).

(7)

Updatef=(Xj∉B,(Xi,Xj)∈,α(Xj)≠

(αupdate(α,Xj,max(()·

α(Xi),α(Xi))-α(Xj))).

(8)

PivotForRelu=(Xi∈B,∃Xl·(Xi,Xl)∈∨
(Xl,Xi)∈,Xj∉B,Ti,j≠0)/
(Tpivot(Ti,j),BB∪{Xj}{Xi})，

(9)

(10)

PivotRelu和ReluSplit在处理的基本原则上仍然与原算法保持一致.

ReluSuccess=(∀x∈,l(x)≤α(x)≤u(x),

∀〈Xb,Xf〉∈,α(Xf)=max(()·

(11)

改进后的Reluplex便具备了验证基于Softplus激活函数的神经网络的能力，此后还能对比这2种激活函数在效果上的不同.Softplus以自身特有的平滑的梯度直接避免了“垂死的Relu”的缺陷[19]，而Softplus的梯度又经常小于1但永远不至于消失，在“均值激活”靠向0时，会使储存信息的矩阵中有很小的非对角数值，从而神经网络的训练速度更快[20-21].Softplus所具有的灵活变化的非线性的导函数也使得神经网络的连接方式更符合其所需的非线性因素[22]，也有利于Softplus激活的神经网络的自我学习能力[23].Softplus较斜率恒定的Relu的平衡性能更强[24]，从而让深度学习的效率进一步提高[25-26].

3.2 算法实现

算法1.设定输出与输入的函数关系的斜率.

① voidexample1_Softplus

②Reluplex←newReluplex(9);

③p←ebound/(1+ebound);

④Reluplex→setSoftplusValue(p);

⑤update(Xb,(1/getSoftplusValue())·

Xf-Xb,true);

⑥ if ((!_dissolvedReluVariables.exists(Xf))

&&reluPairIsBroken(Xb,Xf))

⑦update((Xf,getSoftplusValue·

Xb)-Xf,true);

⑧ endif

如算法1，要更换所验证的激活函数，先将p赋值为Softplus的斜率，随之需把输入变量Xb设定成与输出变量Xf相对应，正好把Xb赋值为(1/getSoftplusValue())·Xf.若Xf并不存在或者Xf与Xb之间的关联性已经丧失，由于原先的输入变量Xb还在，此时将Xf调整为getSoftplusValue·assignment[Xb].

算法2.分配并判断变量是否一致的算法.

① boolReluPairIsBroken(Xb,Xf)

② doublebpoi←assignment[Xb];

③ doublefpoi←assignment[Xf];

④ return (fpoi≠bpoi·getSoftplusValue).

如算法2，Xf≠Xb·getSoftplusValue应该更新，则输出true.

算法3.设定取值上限的算法.

① if (ReluPairs=Xf)/*有待修复的数据作为输出变量的Xf*/

②setupperBounds((1/getSoftplusValue)·

bound);

③ elsesetupperBounds(getSoftplusValue·

bound);

④ endif

如算法3，更新操作之前若需要对Xf更新，那么设定Xb的上标(1/getSoftplusValue)·bound，如果需要对Xb更新，那么设定Xf的上界getSoftplusValue·bound，如此设定神经网络的输出与输入的比率关系.

算法4.根据Xf与Xb的基本条件进行调整的算法.

① if (fpoi≥0) and (bpoi≥0)

② Δb←0;

③ Δf←0;

④ endif

⑤ else if (fpoi≥0) and (bpoi<0)

⑥ Δf←0;

⑦ Δb←(1/getSoftplusValue)·fpoi-

bpoi;

⑧ endif

⑨ else if (fpoi<0) and (bpoi≥0)

⑩ Δb←0;

bpoi;

如算法4，有“Xf≥0，Xb≥0”“Xf≥0，Xb<0”“Xf<0，Xb≥0”“Xf<0，Xb<0”4类条件，都根据具体条件调整Xf与Xb维持其与Softplus激活函数下关系对应.

算法5.积分累加的算法.

①u←ebound/(1+ebound);/*Softplus的斜率先前已赋过值*/

②integral(u(t),i,j,k);/*i是下限，j是上限，k是从下限到上限需经历的次数*/

③ {i←0;

④j←t;

⑤ Δl←(j-i)/k;

⑥t←i;

⑦sum←0;

⑧ for (a←0;a≤k;a←a+1) {

⑧t←t+Δl;/*激活函数的横坐标数值t不断变化*/

⑩sum←sum+u(t) ·Δl;/*对每段积分进行累加*/

为避免计算量无穷大，Reluplex对输入数值的变更过程并非完全连续的，它以10-10为最小单位.如算法5通过积分累加的手段，输入数值在横坐标上每经过极短的长度便更新1次斜率，Xf=Xf+f′(Xb)·setSoftplusValue，依次累加，得到输出变量Xf与输入变量Xb的近似于Softplus激活函数的关系，便能够检验基于Softplus激活函数的神经网络.

算法6先将列链表内的数值都存储在对应的矩阵中，再将需取代的行非空作为整个循环的基本条件，若将被取代的变量与新变量都在同一行，直接删除列链表内被取代的变量并重新调整相关系数.再以函数addEntry重新补充相关系数，将输出变量Xf的系数乘上其在该点的斜率SoftplusValue，结尾清除所有列.

算法6.矩阵操作的算法.

① voidreplaceNonBasicWithAnotherNonBasic

(beReplaced,replace,SoftplusValue)

② while (beReplacedEntry≠NULL)

③current←beReplacedEntry;

④beReplacedEntry←beReplacedEntry→

nextInColumn();

⑤rowcurrent→getRow();

⑥Entry·entryInTarget←NULL;

⑦ if (denseMap.exists(row))

⑧entryInTarget←denseMap[row];

⑨entryInTarget→getRow();

⑩entryInTarget→getColumn();

current→getValue());

SoftplusValue·current→

getValue());

denseMap.clear();

4 实验结果

在原Reluplex求解器中，Reluplex.h是其最主要的源程序，调整Reluplex.h的源代码，使其激活函数由Relu变成Softplus，随后分别对求解器的10个properties脚本文件进行运行测试，获取输出的数据信息与先前Relu激活函数下获取的信息对比分析.还导入别的神经网络TestNetwork.nnet，TestNetwork2.nnet来检验，使得其能更好地显示验证效果.通过在Linux系统下分别测试2种激活函数下的properties脚本文件得到相应的数据输出文件，对其测试效果进行对比评判.

无人机默认由左向右行驶，由神经网络引导无人机躲避别的飞机，神经网络得到冲突解除(clear-of-conflict)信号则会放松警惕，验证无人机是否有潜在的碰撞的可能性，从而训练神经网络的鲁棒对抗性.这10个脚本所对应的10个特性都是无人机防撞系统中的不同基本情况.例如：前2个特性都是入侵的飞机距离较远且速度比无人机慢；第3个至第4个特性都是入侵者在正前方；第5个至第6个特性都是从左侧入侵；第7个至第8个特性都垂直距离过大；第9个特性为从右侧入侵；第10个特性则为入侵者极其遥远.

在图5～10的曲线中，标记为“Softplus”和“Relu”后的数字是与其所对应的测试的第几个脚本文件.横坐标是无人机模拟系统的45个测试点(有的脚本的子程序对数据的约束条件使其仅能检验其中的局部测试点)，纵坐标是各测试点的耗时，达到12 h说明检测超时.每个脚本文件的子程序都设定相应的输入来违反其特性，测试结果为UNSAT表明违反不成功从而特性成立；测试结果为SAT则说明违反特性成功，意味着无人机会有碰撞的风险性.

如图5所示，在第1个特性文件中，Softplus函数则仅有8个测试点超时，其余测试点都得出了UNSAT的结果，而之前采用的Relu激活函数则有20个测试点超时且其他测试点耗时也多于Softplus.

图5 第1个特性下测试点的情况

如图6所示，第2个特性文件是从第10个测试点开始的，Softplus下只有2个超时点，其余测试点都得出了SAT的结果，这与原算法采用Relu激活函数验证的结果完全一样，并比Relu要节省时间.

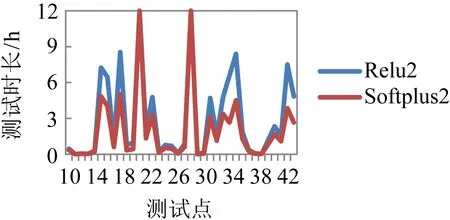
图6 第2个特性下测试点的情况

如图7所示，在第3个特性文件中，Softplus激活函数没有任何超时的测试点，这与之前使用的Relu函数的情况是一样的，并在每个测试点上所停留的时间比Relu要短.

图7 第3个特性下测试点的情况

如图8所示，在第4个特性文件中，除前3个测试点耗时略多些，Softplus激活函数的其余测试点都在25 min以内得到了结果.所有测试点均为UNSAT，与原求解器下Relu的验证情况一样,但相对高效得多.

图8 第4个特性下测试点的情况

如图9所示，T1至T8为8个测试点，这些脚本的子程序仅能检验其中的局部测试点.Softplus激活函数在第6个到第9个特性文件的所有测试点都超时，这与原算法中Relu激活函数的验证结果完全相同.而第5个和第10个特性文件的验证结果则全部得出UNSAT的结果，相对而言原算法中Relu激活函数在第10个特性文件有1个超时点,而在第5个特性文件的各个测试点所花的时间要更多一些.

图9 第5～10个特性下测试点的情况

如图10所示，在新引入不同的神经网络训练数据集后，4个特性文件和其对应的各2个测试点也都得到了其验证结果，均为UNSAT，Softplus没有发生超时情况，并比Relu所花时间要短一些.

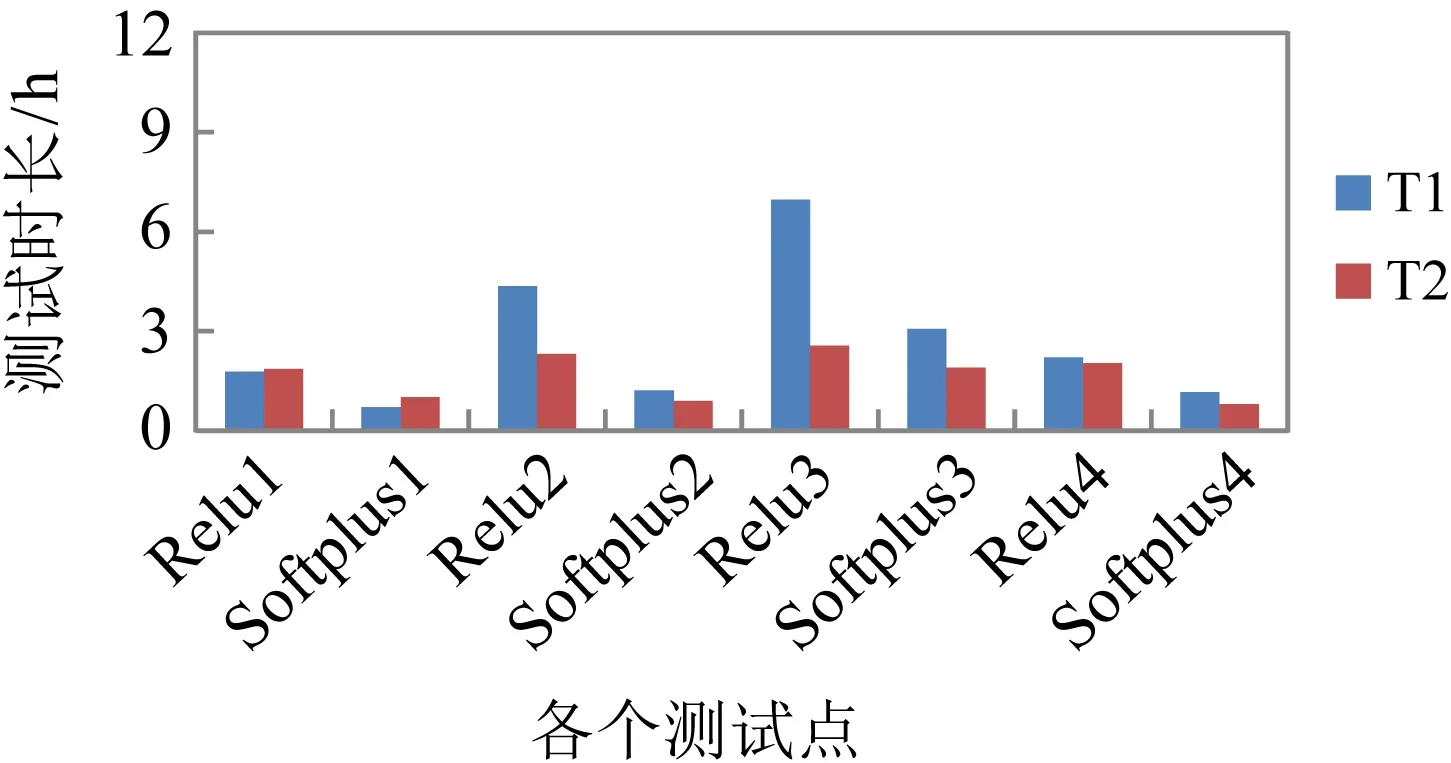
图10 新网络里4个特性下测试点的情况

实验数据证实了改进后的Reluplex算法完全具备验证Softplus激活函数的能力.Softplus函数在大多数测试点中均比Relu函数明显节省时间并成功地解决了局部原本超时而无解的测试点.

5 总 结

使Reluplex能检验Softplus激活函数后，再对基于Softplus的无人机神经网络的所有测试点检测并参照Relu下的结果进行对比研究，可以看出Softplus训练神经网络的成效比Relu要迅速且平稳.

在选择神经网络的激活函数时要尽可能将其平滑化和避免垂死的情况[27].通过对Softplus激活函数的深度神经网络验证研究，扩展优化了对神经网络进行形式化验证的方法，并看到了激活函数不同时所具有的效果，最终成功地检验了神经网络的安全性，证明了该技术在验证现实世界的深度神经网络的可靠性上有着不小的潜力.