应力等效法在单梁静载试验中的应用研究
蒋国富, 卓小丽, 江京翼, 郝天之*,2
(1. 广西交科集团有限公司, 广西 南宁 530007; 2. 广西北投交通养护科技集团有限公司, 广西 南宁 530022)
静载试验是评定桥梁承载能力的最直接、最有效的方法,目前对技术状态不明确的桥梁,或采用新技术、新工艺、新结构或新材料等建成的新型桥梁,或主要结构构件存在潜在损伤的桥梁等情况,多采用荷载试验方法对桥梁进行承载能力评定.盛兴旺等[1]提出了基于P-Δ曲线评估桥梁弹性工作状态的方法;关淑萍[2]对桥梁梁板荷载试验方法及其影响因素进行了分析研究;周勇军等[3]提出了应力等效概念但未对此进行阐述和应用;李凯峰[4]对静动载试验下装配式混凝土箱梁桥的有限元模型修正进行研究.但上述学者均是以《公路桥梁荷载试验规程》(JTG/T J21-01-2015)中校验系数的确定方法为基础进行的研究[5].郝天之等[6]对简支梁裸梁与成桥后梁体应变换算进行了研究(弯矩等效法);提出了采用应变换算对裸梁试验进行了分析,但也仅限于简支结构,对于先简支后结构连续体系未做具体分析.因单梁实际受力特性与成桥受力状态并不相同,仍然采用“弯矩等效法”使得试验荷载计算值失真.为解决上述问题,本文结合一座3~30 m、一座3~20 m和一座3~40 m先简支后连续预应力混凝土箱梁桥的裸梁静载试验控制弯矩进行分析,在文献[6]的基础上,提出了一种更易于工程师理解和应用的计算方法——“应力等效法”.
1 弯矩等效法与应力等效法概述
成桥静载试验以运营状态的汽车荷载效应确定控制荷载效应(常以弯矩表示),再结合荷载试验效率确定试验荷载;单梁静载试验对象为预制梁,在确定控制荷载效应时,除考虑成桥后运营状态的汽车荷载效应外,还需计入尚未施工的恒载效应(如湿接缝、二期恒载等).
常规先简支后结构连续的装配式梁桥,其上部结构由预制状态施工至成桥状态时,结构体系和截面特性均将发生根本变化.
“弯矩等效法”考虑施工过程中结构体系的变化,但不考虑梁体截面特性的变化,仅将各施工阶段增加的恒载及成桥运营状态活载产生的弯矩值累加作为拟试验预制梁的控制荷载效应值,这是不准确的.
“应力等效法”既考虑施工过程中结构体系的变化,同时又考虑梁体截面特性的变化,计算各施工阶段增加的恒载及成桥运营状态汽车荷载对拟试验梁体底面产生的应力增量,并将其折算为预制梁产生等效应力增量时对应的弯矩值,即为拟试验预制梁的控制荷载效应值,据此结合荷载试验效率确定试验荷载.按平截面考虑时应力和弯矩的计算表达式可表示为
式中:σ为拟试验梁体控制截面底面各施工阶段应力增量和;M为拟试验预制梁产生等效应力增量时对应的换算弯矩值(即控制荷载效应值);Mi为控制截面第i个施工阶段增加的荷载产生的弯矩增量;hyi为第i个施工阶段时拟试验梁体控制截面中心轴至梁底面的距离;Ii为第i个施工阶段时拟试验梁体控制截面惯性矩;Wxi为第i个施工阶段时拟试验梁体控制截面抗弯模量;Wx0为拟试验预制梁控制截面抗弯模量;n为用于计算分析的总施工阶段数.
式(1)中相同M作用下σ取决于hy和I或Wxj,如果简单地采用弯矩进行控制,由于hy和I均为变量,应力σ将为不定值,控制不合适将达不到预期的应力要求目标.
以某20 m跨径桥为例,图1a为试验状态,梁高h0=1.2m,hy0=0.738 285 m,I0=0.166 926 m4;图1b为成桥状态(包含混凝土调平层、两侧湿接缝),梁高h2=1.28 m,hy2=0.874 839 m,I2=0.227 996 m4.
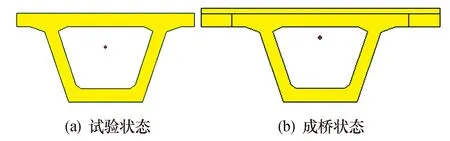
图1 截面特性Fig.1 Section characteristics
仅以成桥后活载效应为例,若活载对试验梁产生的弯矩为M0.
采用“弯矩等效法”计算时,弯矩增量为M2=M0.
采用“应力等效法”计算时,其应力增量为
σ活载=M0hy2/I2=M0/Wx2,σ活载=3.84M0
(3)
根据式(2),在试验梁上产生等效应力对应的弯矩增量MΔ为
(4)
显然以“应力等效法”反算的弯矩增量约为用“弯矩等效法”计算的弯矩增量的87%,说明两种算法的差异非常明显.由于结构的承载能力通常以荷载产生的应力不超过结构材料强度为主要判定标准,为达到相同的应力目标,可通过控制应力σ与h和E的关系反求出控制弯矩M值,从而建立荷载试验效率公式中需要的参数.
2 应力等效法原理及求解方法
2.1 基本原理
常规先简支后结构连续的装配式梁桥,其上部结构由预制状态至通车运营状态的主要施工顺序(不含负弯矩区预应力张拉施工)如图2所示.
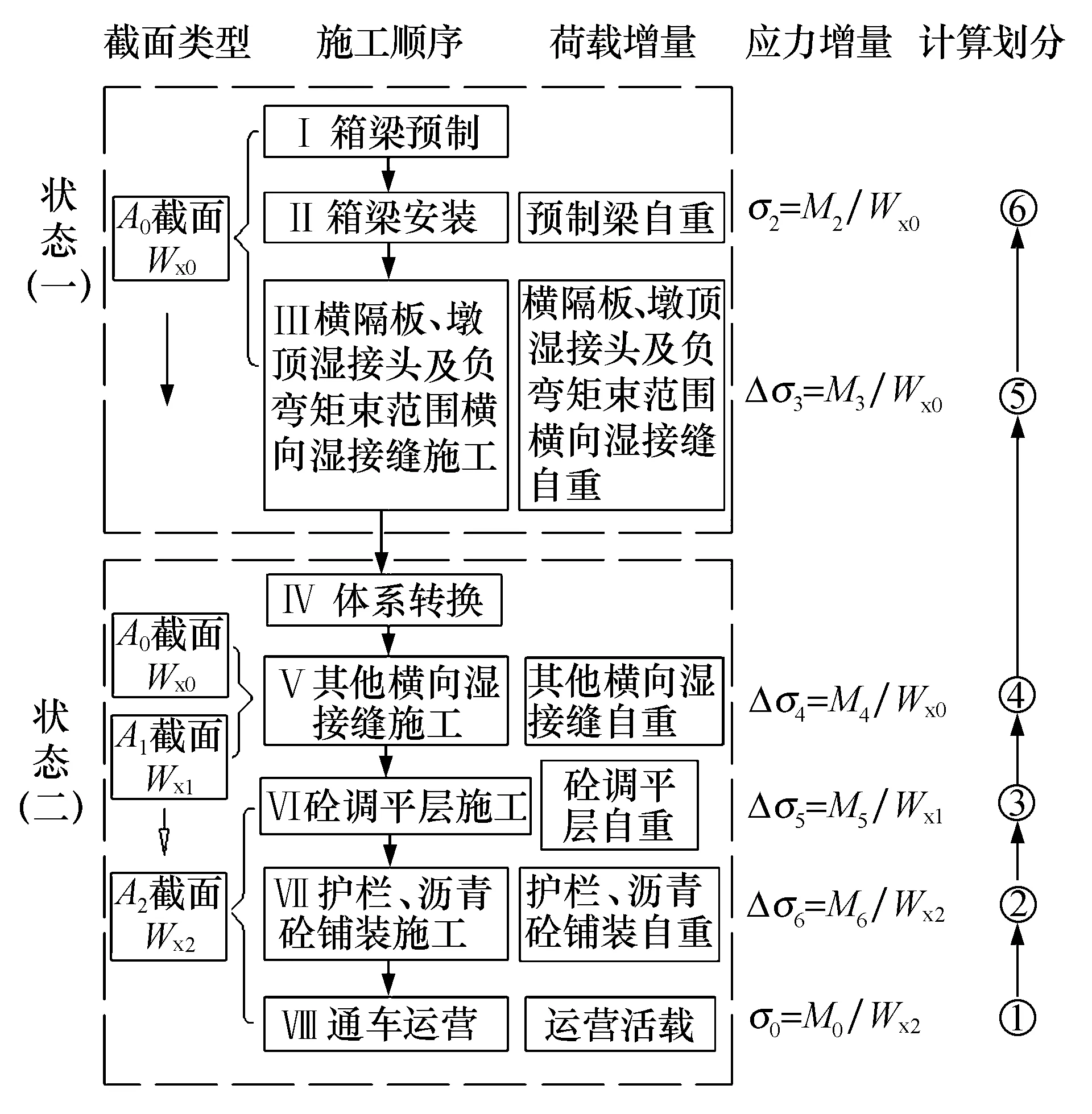
图2 截面类型、施工顺序、荷载增量及计算阶段划分对应关系图Fig.2 Corresponding diagram of section type, construction steps, load increment and calculation stage division
其中,状态(一)为平面状态,按单梁简支受力分析,主要考虑施工阶段Ⅲ增加的恒载对拟试验梁片受力的影响;状态(二)为空间状态,考虑横向、纵向连接的影响,按空间梁格状态受力分析,主要考虑施工阶段Ⅴ、Ⅵ、Ⅶ、Ⅷ增加的二期恒载和通车运营阶段活载对拟试验梁片受力的影响.
在桥梁施工过程中,状态(一)和状态(二)除结构体系变化外,梁体截面特性也发生变化.施工阶段Ⅲ和Ⅴ后梁体翼缘板宽度增加、施工阶段Ⅵ后梁体顶板厚度增加,相应梁体截面特性发生变化.
要想将成桥后连续结构的箱梁的受力情况转换到简支的预制箱梁的受力状态,就必须具体分析箱梁的架设施工至成桥运营过程中的各受力状态,根据箱梁各阶段的应力相等原理折算试验阶段的加载控制弯矩值,进而进行静载试验并根据试验结果评定箱梁的承载能力.
2.2 求解方法
一座先简支后结构连续的装配式箱梁桥一经建成,其连续状态、对同一种荷载工况的横向分布系数很难再改变,进而具体每片梁的控制内力便为一个定值.
根据2.1节基本原理,计算预制箱梁承载能力评价中的静载试验控制内力,就必须从施工顺序和成桥状态入手,首先根据最终成桥状态计算确定待试验梁在活载作用下的最不利位置(本文以控制截面A表示)及梁底应力σ0,再按施工顺序计算各施工阶段下控制截面的梁底应力增量Δσi.计算阶段划分为6个,并假定:1) 某一个阶段浇筑的混凝土,在该阶段不考虑其对截面刚度的贡献;2) 不考虑沥青混凝土层对截面刚度的贡献.试验梁截面类型、施工顺序、荷载增量及计算阶段划分对应关系见图2.施工各阶段中梁体截面变化情况见图3.
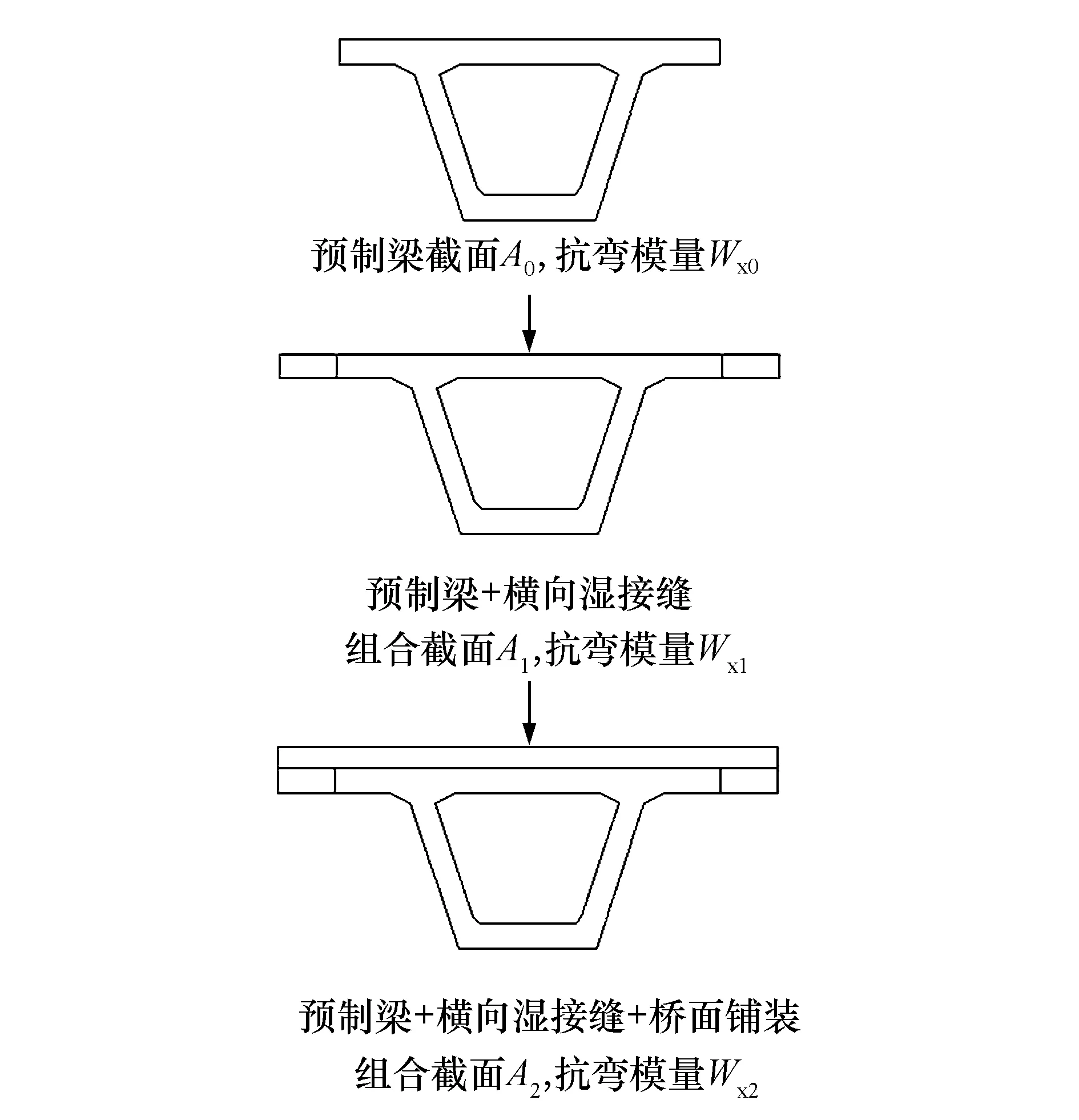
图3 截面变化示意图Fig.3 Schematic diagram of section change
1) 计算阶段①(运营期)主要为通车运营活载在控制截面A处箱梁底面的应力增量σ0,其对应施工阶段为Ⅷ,截面抗弯模量为Wx2;
2) 计算阶段②主要为防撞墙和沥青混凝土铺装层施工在控制截面A处箱梁底面的应力增量Δσ6,其对应施工阶段为Ⅶ,截面抗弯模量仍为Wx2;
3) 计算阶段③主要为混凝土调平层施工在控制截面A处箱梁底面的应力增量Δσ5,其对应施工阶段为Ⅵ,截面抗弯模量为Wx1;
4) 计算阶段④主要为体系转换后,剩余部分湿接施工在控制截面A处箱梁底面的应力增量Δσ4,其对应施工阶段为Ⅴ,此阶段中梁体分两种状态,本阶段浇筑区域的截面抗弯模量为Wx0,而负弯矩预应力束长度范围内的箱梁截面抗弯模量为Wx1;
5) 计算阶段⑤主要为体系转换前横隔板、负弯矩区段湿接缝及连续段接缝施工在控制截面A处箱梁底面产生的应力增量Δσ3,其对应施工阶段为Ⅲ,箱梁截面抗弯模量为Wx0;
6) 计算阶段⑥主要为试验梁的自重在控制截面A处箱梁底面产生的应力σ2(该应力与试验状态的初始应力相同),其对应施工阶段为Ⅱ,箱梁截面抗弯模量为Wx0.
由图2和图3知,施工过程中截面A处的弯矩M和主梁底面的应力σ是变化的,A截面处箱梁底面总应力为
σ总=σ0+σ2+Δσ3+Δσ4+Δσ5+Δσ6
(5)
由于试验箱梁处于σ2状态,因此应力的实际增量为
Δσ=σ0+Δσ3+Δσ4+Δσ5+Δσ6
(6)
根据试验状态时箱梁的抗弯模量Wx0,利用Δσ反求M值即为静载试验的控制内力值,然后根据该内力值进行加载布置.
3 工程算例
3.1 工程背景
某高速公路桥梁,采用3 m×30 m装配式预应力混凝土箱梁,先简支后结构连续;桥面防水及调平层采用8 cm厚C50防水混凝土,桥面铺装采用10 cm厚的沥青混凝土,钢筋混凝土墙式护栏;设计荷载等级为公路-Ⅰ级;桥面总宽为13.0 m.预应力混凝土箱梁的梁高1.6 m,底板宽1.0 m,标准梁间距3.233 m,每两片箱梁间在支点和跨中各设1道横隔板.由于施工管理原因,导致中跨2#梁存在影响承载能力的缺陷,需要对该预制箱梁进行静载试验,评定预制梁箱的承载能力是否能满足设计要求.
3.2 应力等效法求解及分析
1) 控制截面及σ0的确定
根据桥梁最终的成桥状态,计算设计活载作用下2#梁的最大内力及控制截面的位置.计算时首先建立成桥状态模型,并将墙式护栏、不计入刚度的桥面铺装(如沥青混凝土等)以质量的方式施加到结构上计算结构的固有频率,计算活载冲击系数.采用MIDAS/Civil有限元软件建立空间梁格模型进行计算分析,模型见图4.根据计算结果得知中跨2#梁的跨中截面A活载最大效应M0=1 751.1 kN·m,此时箱梁A截面处底面应力σ0为
σ0=M0hy5/I5=M0/Wx2=4.14 MPa
(7)

图4 空间梁格模型图
与软件计算结果4.15MPa基本一致,经核对,其他各阶段中软件计算结果与公式计算基本一致,故本阶段及其他阶段统一采用软件计算值.本阶段软件计算得到的弯矩和应力见图5.
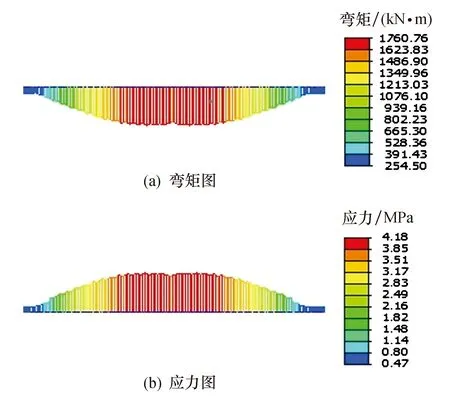
图5 梁格模型、试验梁弯矩及应力图示Fig.5 Beam lattice model, test beam bending moment and stress diagram
2) Δσ6的确定
采用倒拆法进行计算分析,该阶段为连续梁体系,混凝土调平层与湿接缝及主梁形成组合截面受力,计算防撞墙和沥青混凝土铺装层荷载在A截面处产生的弯矩和梁底应力,此时的效应ΔM6=252.1 kN·m,对应的箱梁底面应力Δσ6=0.59 MPa.该阶段弯矩及应力见图6.
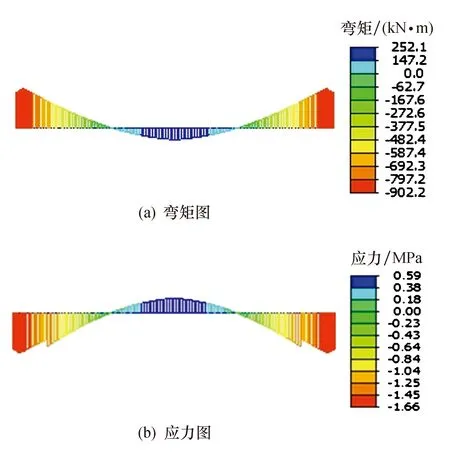
图6 ΔM6及Δσ6图示
3) Δσ5的确定
该阶段为连续梁体系,湿接缝与主梁形成组合截面受力,计算混凝土调平层、防水层荷载在A截面处产生的弯矩和梁底应力,此时的效应ΔM5=147.8 kN·m,对应的箱梁底面应力Δσ5=0.38 MPa,该阶段弯矩及应力见图7.
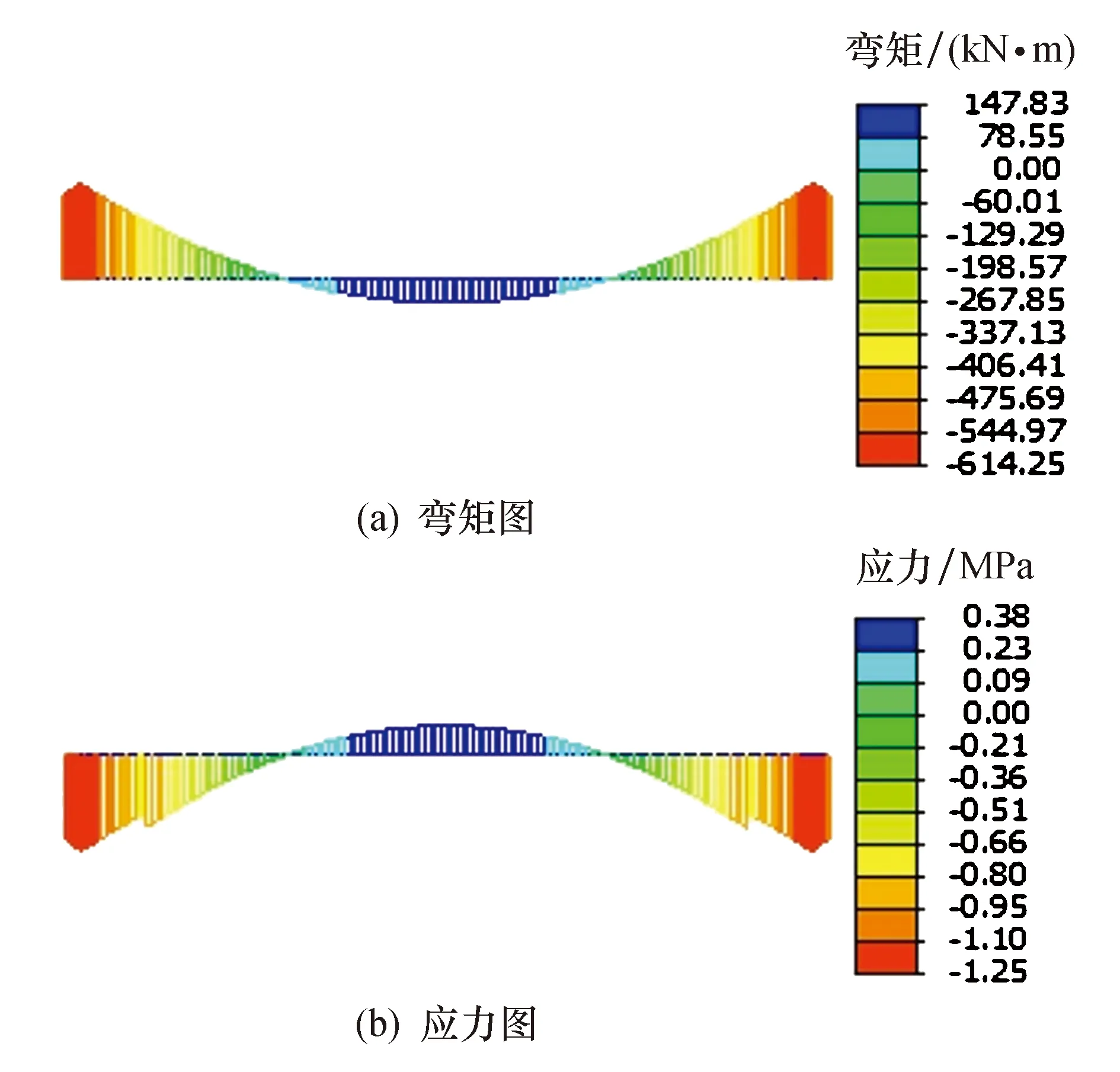
图7 ΔM5及Δσ5图示Fig.7 M5 and Δσ5
4) Δσ4的确定
该阶段为连续梁体系,连续段接头及负弯矩预应力束长度范围内的湿接缝与主梁形成组合截面受力,其它截面为预制梁(裸梁)截面,计算部分湿接缝荷载在A截面处产生的弯矩和梁底应力,此时的效应ΔM4=63.0 kN·m,对应的箱梁底面应力Δσ4=0.17 MPa,该阶段内力及应力类似图7.
5) Δσ3的确定
该阶段为简支梁体系,裸梁受力,计算连续段接头及负弯矩预应力束长度范围内的横向湿接缝、横隔板荷载在A截面处产生的弯矩和梁底应力,此时的效应ΔM3=108.9 kN·m,对应的箱梁底面应力Δσ3=0.29 MPa,该阶段内力及应力见图8.
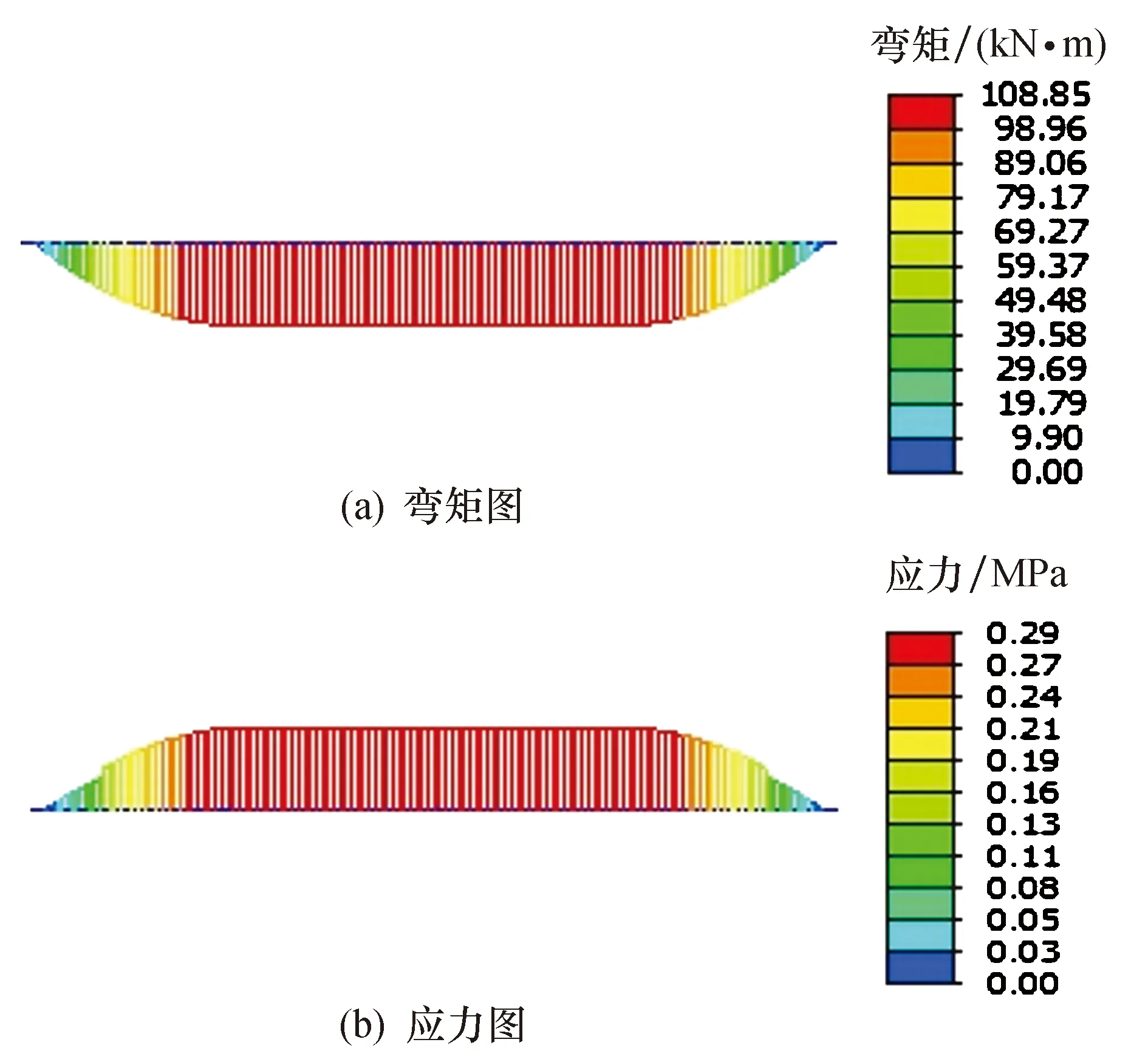
图8 ΔM3及Δσ3图示Fig.8 M3 and Δσ3
6) 控制弯矩的确定
根据以上各施工阶段的计算分析,计算得箱梁的应力增量和Δσ为
Δσ=σ0+Δσ3+Δσ4+Δσ5+Δσ6=5.58 MPa
(8)
各施工阶段的弯矩增量和M2=ΔM,即:
M2=ΔM=2322.9 kN·m
(9)
利用Δσ值反求静载试验的控制弯矩M1为:
M1=Δσ·Wx0=2065.6 kN·m
(10)
采用“应力等效法”反算的弯矩M1与采用“弯矩等效法”计算的弯矩M2,M2比M1大约:
(M2-M1)/M1=12.5%
(11)
以上计算中M1考虑了各施工阶段结构的几何特性变化,比未考虑施工阶段中结构几何特性变化的M2要准确,因此采用M1作为静载试验的控制内力更接近实际,同时也减少了荷载试验的误判.
3.3 跨径对应力等效法求解的影响研究与分析
为进一步分析和验证“应力等效法”和“弯矩等效法”的差异性,及“应力等效法”对不同跨径的响应,特选取目前修建较为广泛的3种跨径的装配式箱梁进行分析.3座桥梁位于同一段高速公路上,净宽相同,设计荷载等级均为公路-Ⅰ级,为更具可比性,本次假设箱梁顶板横坡均为0,采用MIDAS/Civil有限元软件建立空间梁格模型进行分析,并综合考虑横向分布系数的影响,主要成果如表1.

表1 对比分析结果
由上表可以看出,“弯矩等效法”计算结果明显比“应力等效法”计算结果大,且随跨径的增大影响逐渐减弱,但跨径变化对计算结果影响较小.根据式(2)可知:M1的换算与试验状态梁体的抗弯模量Wx0和施工过程中计算时刻梁体的有效抗弯模量Wxi的比值直接相关.通常后期成桥状态的混凝土调平层厚度多在8~10 cm,若其贡献的抗弯模量为Wpz,随着跨径的增大主梁通常采取增加梁高来提高主梁的抗弯模量,达到减小梁底应力目标.显然,主控目标Wx0的增量要远大于Wpz的增量,Wpz在Wxi中的占比将被弱化,即随着跨径增加,Wpz的影响作用将变小.对40 m小箱梁进行计算,以活载为例,根据式(4)计算得:
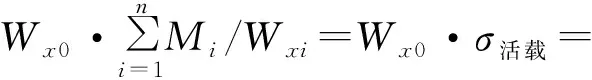
Wx0·M0/Wx2=0.878M0
(12)
与20 m小箱梁计算结果MΔ=0.868M0比较,相差1%.
根据以上分析可知:
1) 3种跨径的桥梁按以上两种计算方法的计算结果偏差均在12%左右,且结果偏差有随跨径增加而逐渐减弱的趋势,但跨径变化对计算结果的影响较小;
2) 不同施工阶段梁体几何特性会发生变化,部分后期施工的混凝土将与预制梁组成联合截面,并分担部分施工荷载和后期活载产生的效应,从而降低预制梁承担的总荷载效应;
3) “应力等效法”考虑更为周全和准确,可避免因控制弯矩过大(“弯矩等效法”导致控制弯矩偏大)而导致的加载过大,从而减少荷载试验的误判和降低加载成本.
4 结论
本文根据预制箱梁试验时至成桥各施工过程中的结构几何特性不同,对梁体受力进行了详细分析和研究,通过采用“等效应力法”和“弯矩等效法”对梁体受力计算分析,并以具体计算结果进行对比分析,得到了一些有益结论:
1) 横向湿接缝、桥面调平层等后期浇筑的混凝土会与预制梁组成联合截面,并分担部分施工荷载和后期活载产生的效应,已影响到采用“弯矩等效法”计算控制内力的准确性;
2) “等效应力法”计算单梁静载试验控制内力时,以应力计算为准,综合考虑了梁体施工过程中结构的几何特性变化,计算过程和结果更加符合结构的实际受力状态.
3) “弯矩等效法”计算结果比“应力等效法”计算结果大12%左右,采用“应力等效法”计算可减少荷载试验的误判和降低加载成本.
4) 单片简支梁静载试验以应力作为控制指标,可有效避免结构计算失真,目标更为直观.

