双回路线圈连续移动感应加热的数值分析
谌卓豪, 谢 晖,2
(1. 湖南大学 汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082;2. 大捷智能科技(广东)有限公司, 广东 佛山 528225)
感应淬火是利用电磁感应加热的原理,以电涡流的形式迅速提高工件表面温度,而后快速冷却的一种表面热处理工艺。感应淬火能有效提高工件表面的硬度、耐磨性和抗疲劳强度,同时使工件心部保持较高的韧性[1]。
国内外学者针对不同的应用领域设计了多种形状的感应加热线圈,并采用数值模拟的方法对工件表面感应淬火的温度分布进行了多方面的研究。Li等[2-3]使用多根并排的长直铜管线圈对汽车B柱进行感应加热,在铜管线圈的不同位置加装导磁体环,并建立有限元数值模型研究B柱感应加热的温度分布,发现可以在线圈不同位置上加装导磁体环对B柱进行局部加热,以满足区域温度定制的要求,并通过改进加热线圈上导磁体环的布置制定出满足汽车B柱淬火需求的新工艺。Sun等[4]建立电磁场—温度场—应力场的多场耦合模型研究重型气缸的感应加热过程,研究结果表明,使用矩形线圈会引起明显的尖角效应,导致重型气缸的末端出现过热和过烧现象,通过在线圈上加入热处理环和导磁体可以削弱尖角效应的影响。Song等[5]针对轴类零件感应加热设计了等节距线圈、变节距线圈和变半径线圈并建立感应加热数值计算模型,计算结果表明,与等节距和变节距线圈相比,变半径线圈可以减小零件轴向温差。在合适的电流密度和电流频率下,使用变半径线圈加热的工件可以获得更均匀的温度分布。
此外,不少学者研究了使用不同形状感应线圈对齿轮、轴承、曲轴等工件感应淬火时,工件表面的温度场分布,以此优化淬火工艺和改进淬火线圈的结构,并取得了良好的效果[6-8]。感应淬火在不同应用领域所使用的加热线圈形状有很大差异,加热线圈的形状和尺寸则会直接影响工件的温度分布和淬火的加热效率[9]。小尺寸双回路加热线圈具有加热效率高、淬火型面适应性强的优点,结合连续移动局部感应加热的新技术[10-12],将适合用于批量小且形状多变的汽车模具表面热处理。
本文针对汽车模具表面淬火领域,选取模具整形面和修边刃口表面淬火两种典型工况,以双回路线圈为热源,使用有限元仿真软件建立电磁场与温度场双向耦合的连续移动感应加热模型,研究小尺寸双回路线圈在汽车模具表面连续移动感应加热的温度分布。
1 数学模型
1.1 电磁场
根据电磁场理论,汽车模具感应淬火过程中的电磁模型可以用微分形式的麦克斯韦方程组来描述:
高斯磁通定律:
∇·B=0
(1)
高斯电通定律:
∇·E=0
(2)
法拉第电磁感应定律:

(3)
安培环路定律:
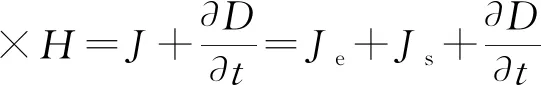
(4)
式中:B为磁通密度;E为电场强度;H为磁场强度;D为电通密度;J为传导电流密度,由涡电流密度Je和源电流密度Js组成;t为时间。与传导电流密度相比,位移电流密度∂D/∂t可以忽略不记,可将式(4)简化为:
∇×H=Je+Js
(5)
引入本构关系:
B=μH=μ0μrH
(6)
J=σE
(7)
式中:μ为磁导率;μ0为真空磁导率;μr为相对磁导率;σ为电导率。
为简化计算,引入磁势矢量A并表示为:
B=∇×A
(8)
同时工件内的涡电流分布可以表示为:
(9)
因此,涡流区的电磁场方程可以描述为:

(10)
1.2 温度场
汽车模具感应淬火过程中的温度场可以用三维非稳态导热微分方程来描述:

(11)
式中:ρ为模具材料的密度;c为模具材料的比热容;T为模具的瞬态温度;λ为模具材料的导热系数;qv为模具内的体积能量密度,此处表示感应涡流产生的焦耳热。
在感应加热过程中,还需要考虑模具外表面和环境之间的对流传热和辐射散热,可以用公式(12)和公式(13)来描述温度场的边界条件:
qc=h(T∞-Ts)
(12)
(13)
式中:qc为单位面积对流换热热流密度;h为对流换热系数;T∞为环境温度;Ts为模具表面温度;qr为单位面积辐射热流密度;ε为发射率;δ为斯提芬波尔赫兹常数。
2 模型建立
2.1 几何模型
选取长方体工件为研究对象,分别以工件中心和边缘两个位置的表面淬火代表模具整形面淬火和模具刃口淬火,研究模具在使用双回路线圈淬火时的温度分布。以模具整形面淬火为例,建立连续移动感应加热的有限元计算模型如图1所示,模型由双回路线圈、导磁体、工件和空气域4部分组成。图1中P1、P2分别为双回路线圈在连续移动感应加热的起始位置和结束位置,在淬火过程中,工件保持不动,感应线圈从P1点开始加热,并以5 mm/s的速度自左往右移动,移动至P2点时停止加热,仿真结束。在整个数值计算过程中,感应线圈输入电流的大小为1500 A,频率为30 kHz,感应线圈与工件之间保持1 mm的间距,设置环境温度为20 ℃。

图1 感应加热有限元计算模型
有限元计算模型中,导磁体和双回路线圈的基本几何数据如图2所示,模型的材料信息和其余的尺寸数据为:①工件材料为球墨铸铁GGG70L,尺寸为80 mm×80 mm×30 mm;②导磁体材料为铁氧体;③线圈材料为脱氧铜,方形空心线圈,壁厚0.5 mm。

图2 双回路线圈和导磁体的几何数据
2.2 数值分析流程
图3为球墨铸铁GGG70L的材料属性参数随温度的变化曲线[13],其恒压热容、磁导率、电导率和热导率随温度的升高呈非线性变化,会对感应加热的温度分布产生较大的影响。为此,需要建立电磁场与温度场双向耦合的数值计算模型,其计算流程如图4所示。首先根据初始条件求解电磁场,将电磁场求解得到的焦耳热作为当前时间步工件内的体积能量密度输入到温度场,并根据三维非稳态导热微分方程计算工件的温度分布。在下一个时间步,先根据工件的温度分布,更新材料属性参数,再按上述流程重新求解电磁场和温度场,往后不断计算每一个时间步的解,直至到达设定时间,求解完成。
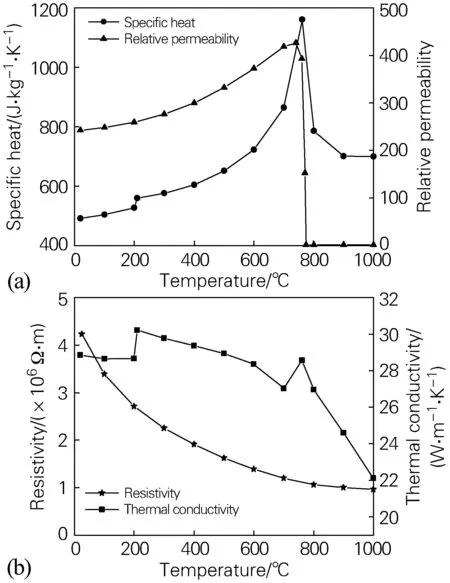
图3 GGG70L球墨铸铁的材料属性参数

图4 耦合计算流程
3 结果分析
3.1 电磁场
3.1.1 初始涡流
图5是感应淬火初始时刻,工件中心和边缘两个位置在双回路线圈感应加热时的涡流分布图。此时电流由线圈右端输入,左端输出,在双回路线圈中呈逆时针流动,工件受电磁感应作用,在表面产生与线圈形状相似的顺时针涡流,且沿线圈向外涡流值逐渐减小。对比图5(a,b)可以发现,M2区域的涡流值(约7.0×108A·m-2)略大于M1区域的涡流值(约6.5×108A·m-2),说明双回路线圈在工件边缘的直角位置进行感应加热时,会受到尖角效应[14]的影响,工件直角位置涡流更密集,加热效果更明显。
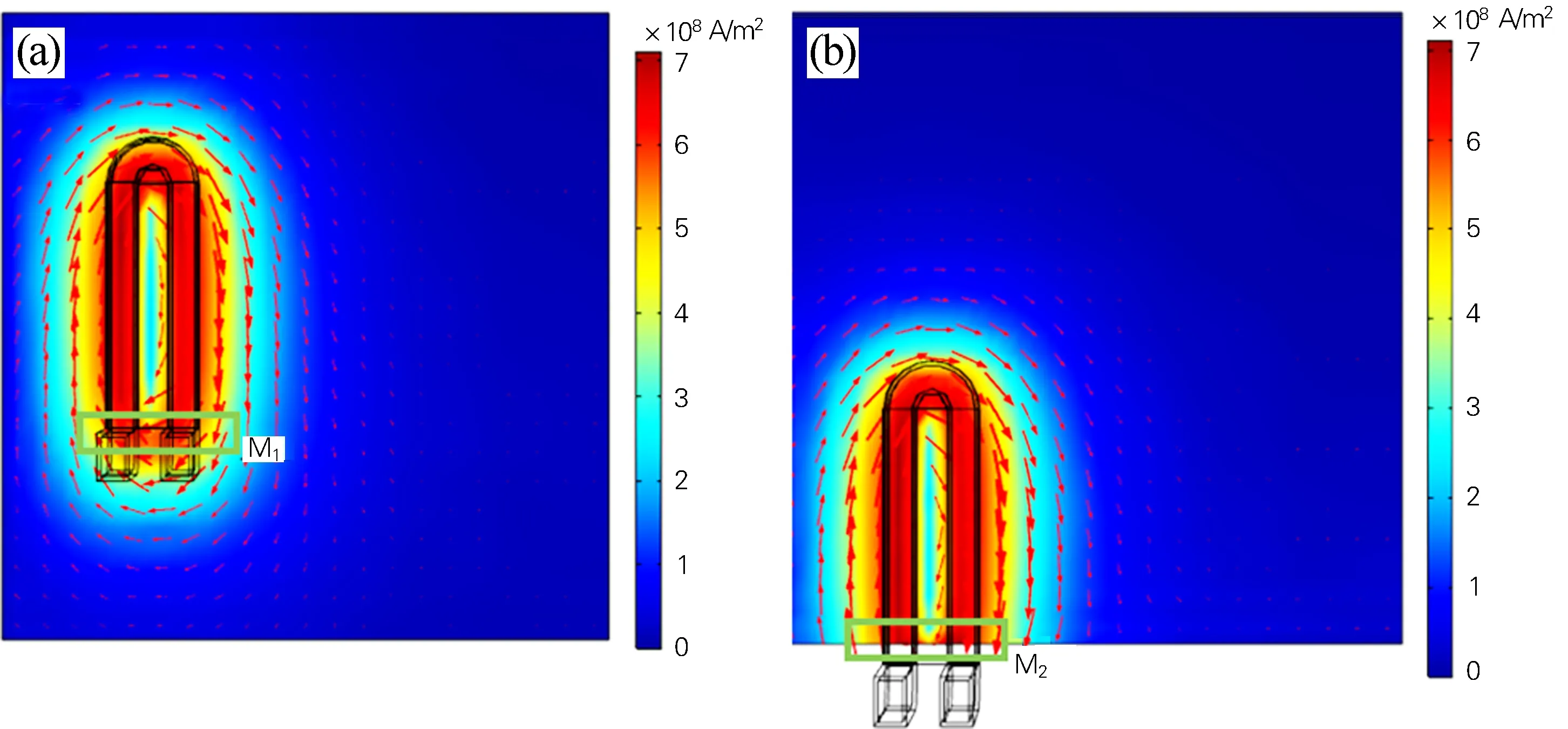
图5 工件初始时刻的感应涡流分布
3.1.2 最大涡流
图6为感应加热过程中,工件的最大涡流密度随时间的变化。可以发现,工件中心和边缘感应加热的最大涡流变化规律大致相同,在初始时刻涡流值较大,随感应加热的进行,工件温度升高,涡流值降低。以工件中心位置感应加热为例,可以发现,从0~2 s,最大涡流从7.80×108A·m-2迅速降低到3.74×108A·m-2,主要原因是随着感应加热的进行,工件表面的温度迅速升高,材料电导率随温度的升高逐渐降低,导致涡流值迅速减小。随着双回路感应加热线圈沿工件表面自左往右移动,在2~10 s,涡流值在3.74×108A·m-2附近呈现小幅度波动,说明双回路线圈连续移动感应淬火的过程中,工件表面的最大涡流值可以达到一个相对稳定的状态。

图6 工件不同位置最大涡流密度随时间的变化
3.2 温度场
3.2.1 表面温度分布图
图7为工件中心和边缘两个不同部位在双回路线圈感应淬火时的温度分布。为方便描述,将双回路线圈分成左线圈、右线圈和顶部的半圆线圈3部分。以工件中心位置感应加热为例,在0.5 s时,线圈移动距离为2.5 mm,此时工件中心的加热区域温度约为550 ℃,加热区域基本保持在线圈正下方,表现为椭圆外形。随着双回路线圈沿工件表面自左往右移动,在5 s时,有效加热区域表现为左线圈扫过的区域,在左线圈正下方偏左约2 mm位置出现一个超过900 ℃的高温区域,说明移动式感应加热的高温区域出现位置会滞后于线圈覆盖区域,但滞后现象并不明显。

图7 工件不同时刻的温度分布
对比工件中心和边缘直角感应加热的温度分布,可以发现,工件边缘直角处受尖角效应的影响较大,在0.5 s时温度已经达到700 ℃,明显高于其他加热区域。在5 s时,受加热的直角部位出现一个超过1000 ℃的高温区域,该高温区域会导致线圈覆盖区域的温度分布均匀性下降,一定程度上影响工件边缘直角部位的淬火质量,这也是模具刃口在使用双回路线圈淬火时容易产生裂纹和出现过热的主要原因。
3.2.2 最大温度
图8为双回路线圈在工件不同部位感应加热过程中,工件的最高温度和时间的关系,可以看出工件中心和边缘感应加热的最高温度变化规律基本是一致的,但受尖角效应的影响,工件边缘直角处淬火时的最高温度会略高于工件中心位置淬火的最高温度。以工件中心位置感应加热为例,在0~2 s,最高温度迅速增加并达到峰值,在随后的2~10 s,最高温度维持在950 ℃附近,呈现小幅度波动,说明双回路线圈在连续移动感应加热时,淬火温度会到达一种稳定状态。相比传统的火焰淬火,使用双回路线圈对模具进行移动式感应淬火,可以在一定的工艺条件下得到稳定的淬火温度,这将有利于实现淬火的机械化和自动化,并能获得更均匀的淬火质量,延长模具的使用寿命。

图8 工件不同位置的最高温度随时间的变化
3.2.3 工件不同深度的温度分布
在工件距离双回路线圈初始位置30 mm的位置设定6个不同深度的测温点A~F,图9(a)为工件中心位置感应加热过程中,不同深度的温度随时间的变化规律。A1~D1点深度小于2 mm,位于工件集肤深度内,其温升主要受感应涡流的影响,随着深度的增加,达到的最高温度逐渐降低。在整个加热过程中,工件表层温度出现两个峰值,温度变化过程可以分为5个阶段:

图9 工件不同深度的温度分布
1) 0~4.8 s,线圈从初始位置自左往右移动,逐渐接近但并未到达测温点上方。此阶段测温点受电磁场的影响较小,产生的感应涡流和焦耳热较小,热量主要来自测温点左侧已加热区域的固体传热,温升速度和幅度较小。
2) 4.8~5.6 s,右线圈经过测温点上方,此阶段集肤深度内测温点处产生非常大的感应涡流,温升速度最快,温度出现第1个峰值。此过程可以看作感应加热过程的一个预热,先依靠右线圈将工件加热到一个比较高的温度,再通过左线圈将工件加热到淬火所需温度。预热有利于工件进行热传导,增加淬硬层深度,同时提高加热均匀性,减小加热畸变[15]。
3) 5.6~6.4 s,右线圈离开测温点,此时测温点位于左线圈和右线圈之间的间隙下方,涡流值相对较小。受空气自然对流、热辐射和热传导的影响,此阶段出现短暂的温度下降。
4) 6.4~7.2 s,左线圈经过测温点上方,测温点处涡流值增大,温度再次升高,此过程中温度出现第2个峰值,并达到淬火的最高温度。相比第二阶段,该阶段温升速度和幅度更小,主要是因为:①该阶段工件表面的温度已经到达材料的居里温度,材料的相对磁导率降为1,导致作用于集肤深度内的感应加热功率下降;②工件的电导率随温度升高而降低,导致该阶段的涡流值相对较小;③该阶段测温点处温度和周围环境温度差异更大,由热传导、热辐射和热对流引起的散热效果更明显。
5) 7.2~10 s,左线圈离开测温点上方,测温点处感应加热结束,温度逐渐降低。
图9(a)中E1、F1两点位于工件集肤深度外,随深度的增加,温度逐渐降低,其温升曲线只出现一个峰值,这是因为在集肤深度外,工件的加热主要依靠集肤深度内高温区域的固体热传导,这也导致了工件集肤深度外的最高温度出现时间(7.6 s)要滞后于集肤深度内的最高温度出现时间(7.2 s)。
图9(b)为工件边缘感应加热过程中,工件直角处不同深度的温度随时间的变化规律。可以发现,直角处不同深度测温点的温升曲线均为单峰值曲线,这是由于工件直角处在淬火过程中会出现尖角效应,导致直角处的涡流更加密集。当测温点位于左右线圈之间的间隙下方时,直角处依然汇集很大的涡流密度,温度保持上升趋势。随深度的增加,直角处的温度也逐渐降低,但相比工件中心位置,随深度增加其温度下降的幅度更小,拥有更大深度的高温区域,便可获得更大的淬火深度。因此,对部分淬火要求较低的模具刃口,可以使用双回路线圈替代定制的直角仿形线圈沿刃口直角的一侧进行淬火,这样能够在获得满足刃口淬火要求的淬硬层深度的条件下,省去拆卸更换感应线圈的操作步骤,有效提高淬火的作业效率。
4 试验验证
为进行试验测试,制作带导磁体的双回路感应线圈并将其安装在感应器上,使用工业机器人控制感应器和感应线圈运动,确保感应线圈沿GGG70L球墨铸铁样件表面匀速移动,对表面进行感应淬火。淬火过程中,使用红外测温仪测量工件表面的温度。由于红外测温受到双回路线圈和导磁体的阻挡,无法测量线圈正下方的工件温度,试验时将红外测温点设定在线圈左侧1 cm处,并跟随线圈自左往右移动。试验选用工艺参数为:电流频率为30 kHz,电流大小为1500 A,线圈移动速度为5 mm/s。温度测量结果和仿真模拟结果的对比如图10所示,仿真计算结果和试验测量结果大致相同,最大误差为6%,表明数值模拟计算的结果是可靠的。

图10 淬火过程中工件表面温度测量结果与数值模拟计算结果对比
5 结论
1) 双回路线圈的感应加热区域基本保持在线圈正下方,表现为与线圈外轮廓相似的椭圆外形。
2) 使用双回路线圈进行连续移动感应加热,工件最高温度会在2 s时到达最大值,随后保持一个相对稳定的状态。通过控制淬火工艺,可以获得稳定的模具淬火温度,提高淬火质量。
3) 在模具整形面淬火时,集肤深度内热量主要来自感应涡流产生的焦耳热,温升曲线表现为带预热的双峰温度曲线,集肤深度外热量主要来自高温区的热传导,温升曲线表现为单峰温度曲线。
4) 在模具刃口淬火时,有比较明显的尖角效应,温升曲线表现为单峰曲线,容易出现过热现象,影响淬火均匀性。

