多属性相似度一致性投影决策法

郑诺希, 李 武, 周小强, 刘 钢

(湖南理工学院信息科学与工程学院, 湖南 岳阳 414000)

0 引 言

在工程、管理、经济、军事等领域,人们面临许多多属性决策与评价问题,很多学者进行了大量的理论研究和方法探索。文献[4]结合文献[7]对评价数据进行规范化处理,把评价向量在理想向量上的投影作为综合评价标准,以此来评价备选方案或候选对象的优劣,即投影决策法。随后,诸多学者对投影决策法进行了研究,从不同方面进行了改进、扩展或应用。

文献[8]基于投影决策法提出了主成份投影法,旨在解决属性间的信息重叠问题。文献[9]结合数学规划模型,便于处理区间数属性权重不确定问题。文献[10]进一步讨论了基于投影的区间数评价。文献[11]结合数学规划和区间型理想点,提出了基于投影的区间型多属性决策两阶段优化模型。文献[12]为了避免模糊矢量之间进行比较,建立了一种新的模糊矢量投影评价法。文献[13]进一步扩展到三角模糊数,提出了一种基于线性规划和投影的模糊多属性决策新方法。文献[14-15]将投影决策法扩展到直觉模糊数和区间直觉模糊数。还有一些学者提出了多种针对其他决策数据类型的投影决策法。值得注意的是,矢量投影法与灰色关联理论结合也取得了一定的研究成果。投影决策法及其扩展方法在效能评估、装备方案评价、可持续技术方案、风险分配等方面都有很好的应用。

文献[35]考虑到正负理想点,在空间上构造了一种综合评价方程,很好地从侧面验证了文献[4]的有效性。文献[36]针对文献[4,35]存在决策向量在理想向量上投影值相等而无法判断方案的优先顺序的问题,提出了一种新的带距离相似度的投影决策法。文献[37]指出文献[36]引入的距离相似度会导致新的问题产生,针对此提出了一种新的余弦相似度与距离相似度相结合的方法。文献[38]在犹豫模糊信息下,融合了逼近理想解排序(technique for order preference by similarity to ideal solution, TOPSIS)思想,提出了一种折中的双向投影法。文献[40]考虑到决策者的偏好,强调了模相似度,提出了一种新的带模相似度的投影决策法。然而,上述相关投影决策法及衍生方法关注到向量相似度及组合方法不够全面会产生空间评价失效的情况,从而导致某些评价数据失效,这样有时会导致违背决策者的意愿或者出现异常的评价结果。

因此,本文结合矢量投影思想、距离测度、向量相似度、决策者偏好对其进行改进,提出理想偏移向量的定义,构造新的综合评价函数。本方法对模相似度、距离相似度、余弦相似度和方向相似度进行综合考虑,对理想向量进行调整,既能更好地反映评价向量与理想向量的接近程度,还有利于融入决策者的偏好。

1 预备知识

1.1 问题描述

设多属性决策的方案集为={,,…,},属性集={,,…,},决策矩阵为={}×。

设={,,,},其中(=1,2,3,4)分别表示效益型、成本型、固定型以及区间型属性集。对不同的属性进行规范化处理:

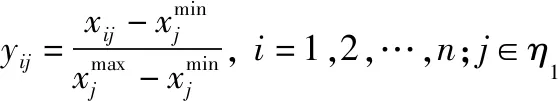
(1)

(2)

(3)

式中:为属性的最佳稳定值。

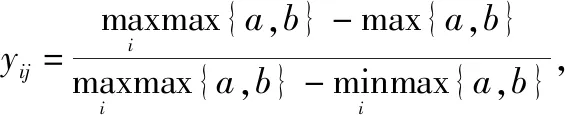
(4)

式中:[1,2]为属性的最佳稳定区间。

由规范化后的矩阵={}×,可知各个方案的决策向量=(1,2,…,)。由文献[7,36]可知,采用式(1)～式(4)分别对效益型、成本型、固定型以及区间型属性值规范化后,属性值最大均为1,最小均为0。显然,各评价属性的理想属性值为

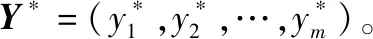
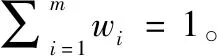
1.2 现有方法的相关分析

设第个决策向量与理想向量之间的夹角为,如图1所示。

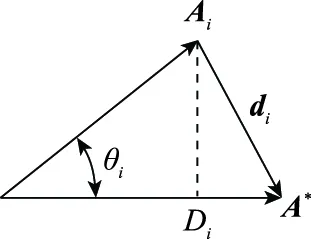
图1 决策向量Ai与理想向量A*的几何关系示意图Fig.1 Schematic diagram of geometric relationship between decision vector Aiand ideal vector A*

则决策向量与理想向量的夹角余弦为

(5)

记决策向量到理想向量的距离向量为

=-

(6)

决策向量在理想向量上的投影为

(7)

式(7)表明:当余弦相似度(非负)相等时,决策向量的模越大,则方案越优;当决策向量的模相等时,余弦相似度越大(即夹角越小),则方案越优。但式(7)无法有效评价模相似度小但余弦相似度大或模相似度大但余弦相似度小的情况。

文献[35]考虑到TOPSIS法的空间特性,构建了一种综合评价方程,即正交投影法,可得决策向量的综合评价函数:

(8)

由式(8)可知,文献[35]强调了方案与负理想解的关系,遍历所有方案之后得到的正负理想解是固定的,从侧面验证了文献[4]的可取之处。

文献[36]指出文献[4,35]给出的决策向量在理想向量上的投影值有时不能对决策向量进行排序。例如,图2中=。

图2 决策向量Ai在理想向量A*上投影值相等的情况Fig.2 The case where the decision vector Aihas the same projection value on the ideal vector A*

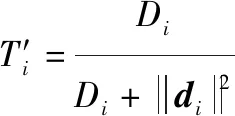
(9)

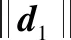
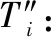
(10)

式(10)表明:当余弦相似度(非负)相等时,距离相似度越小,则方案越优;当距离相似度相等时,余弦相似度越大,则方案越优。但式(10)无法有效评价距离相似度和余弦相似度同时都小或同时都大的情况。

文献[38]借鉴了TOPSIS等方法的贴进度测算公式,同时考虑遍历所有方案的正负理想点,提出了一种折中的双向投影法,即定义了决策向量的综合评价函数:

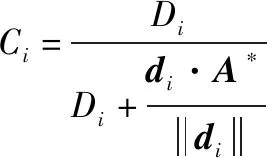
(11)

由式(11)可知,文献[38]很好地解决了决策向量在理想向量上投影值相等的问题,但忽略了文献[4]方法的优越性,导致容易引入新的问题,例如第4节案例及分析部分某些投影值小但距离相似度大的情况。

文献[40]强调了模相似度,即定义了决策向量的综合评价函数‴:

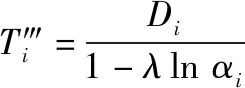
(12)

式中:∈[0,+∞);

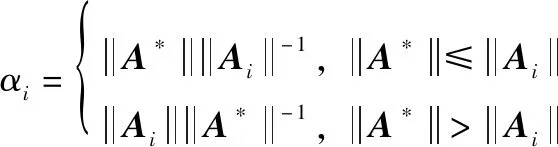
式(12)表明,根据的不同,综合评价函数‴倾向于投影一致性或者模相似度一致性。

但对于图3中的例子,余弦相似度为零导致投影为零,式(7)～式(12)会导致综合评价函数失效,从而文献[4,35-38,40]都无法有效评价。

图3 投影相等并且夹角为90°的情况Fig.3 The case when the projections are equal and the included angle is 90°

为此,本文将决策向量在理想决策向量上的投影思想与向量接近程度结合起来,给出一种多属性决策与评价的新方法,能解决上述无法进行综合评价的问题。

2 相似度一致性的投影决策方法

2.1 理想偏移向量

由式(6)可知:理想向量是由评价向量与距离向量组成的。则理想偏移向量可定义为

=+=(1-)+

(13)

式中:∈[0,+∞),且与理想向量的偏移程度有关。当接近0时,理想向量向决策向量靠近;当=1时,=表明理想向量无偏移;当远离1趋向于+∞时,理想向量向决策向量远离。理想偏移向量通过参数可对理想向量的模、方向进行调整,从而调整与决策向量的模相似度、距离相似度、余弦相似度和方向相似度之间的权重。

2.2 改进的投影决策法

基于理想偏移向量,下面定义一种决策向量的综合评价函数:

(14)

设={=|=1,2,…,},∈[0,+∞),为待评估和决策方案的个数,是偏好系数。当越接近0时,决策者越倾向于决策方案与理想方案的模相似度的一致性;当从右边临近1时,决策者倾向于决策方案与理想方案的距离相似度的一致性;当越趋向于+∞时,决策者越倾向于决策方案与理想方案的方向相似度的一致性。特别地,如果=1,那么=,和文献[4]中综合评价函数一致,即式(7)综合了模、方向的评价,表明决策者完全忽视了文献[4]的不利影响。

2.3 多属性评价步骤

基于以上理想偏移向量和综合评价函数,多属性评价基本步骤如下。

根据决策者的偏好确定偏好系数。

按照值的大小进行评价与决策。

3 有效性分析

3.1 决策向量与理想偏移向量的关系

决策向量与理想偏移向量之间的几何关系如图4所示。

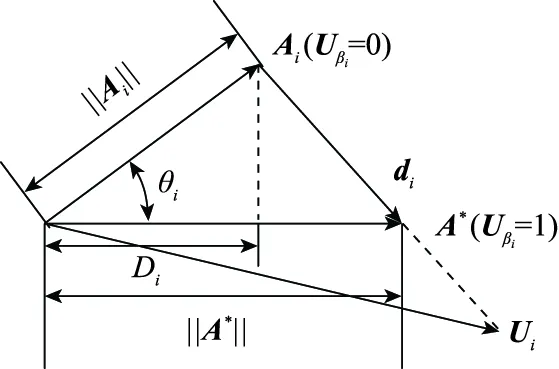
图4 决策向量Ai与理想偏移向量Ui之间的几何关系Fig.4 Geometric relationship between the decision vector Aiand the ideal offset vector Ui

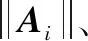
(1) 由可以计算出:

① 当=1时,则=1=,反之也成立。

② 当=0时,则=0=,反之也成立。

③ 可得:

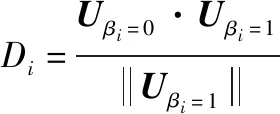
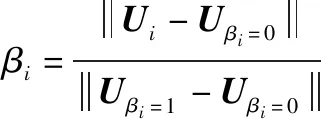
==1-=0

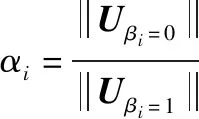
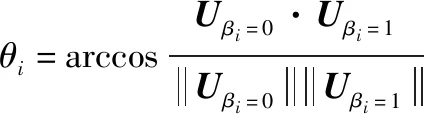
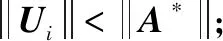
综上所述,本文给出的理想偏移向量具有调节作用。由式(7)～式(12)可知:文献[4,35-38,40]给出的方法各有优势,但本文基于理想偏移向量构造的一种新的综合评价函数集成了文献[4,35-38,40]的优势,起到了改进、扩展和补充的作用。

3.2 决策向量之间的评价关系

决策向量之间的综合评价效果如图5所示。

图5 决策向量之间的综合评价效果图Fig.5 Comprehensive evaluation effect diagram between decision vectors

在平面几何中,向量之间不仅存在模和方向的差异,还存在距离测度的不同。当一个方案3个方面的相似度都优于另一个方案,则能直接评价两个方案的优劣;当一个方案3个方面的相似度不劣于并有至少一个方面优于另一个方案,如图5所示,从直观上也能评价两个方案的优劣。因此,考虑在空间评价中方案至少存在一个方面的差异,同时研究模长、方向和距离测度的评价方法显得十分有必要。

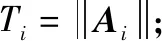
其次,由图5可知,当在临近1时,1=1(2=1)>5=1>3=1(4=1)能使相对综合评价位置不变;当从右边靠近1时,2>1>1>1>5>1>3>1>4>1,这体现了决策者注重距离相似度的评价;当从左边靠近1时,1<1>2<1>5<1>4<1>3<1,这体现了决策者注重模相似度的评价。

然后,综合式(10)和图5可以判断,单一相似度的衍生综合评价标准可能会导致评价失效。

最后,通过图5可以得出,数据尺度的不同将直接影响数据综合评价失效的数量。例如百分制评分和十分制打分的数据分布离散程度是不同的。

4 案例及分析

4.1 案例分析

为了方便比较,本文选用文献[4]中1992年我国16个省份主要工业经济效益的统计数据(见表1)。

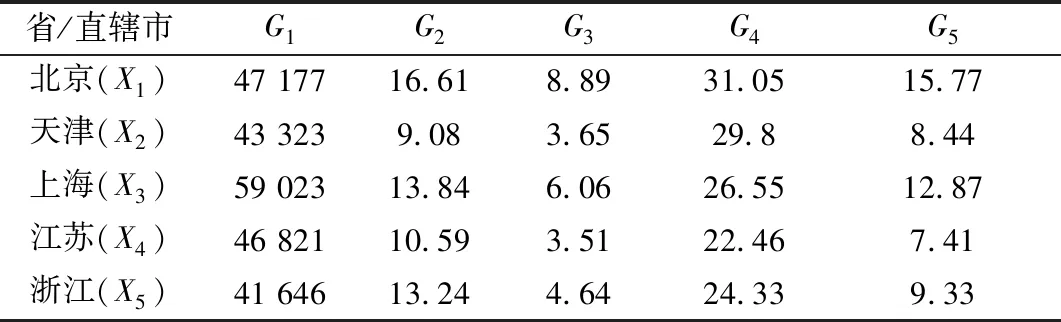
表1 1992年全国部分省、直辖市主要工业经济效益指标Table 1 Comparison of main industrial economic benefit indexes in some provinces and municipalities of China in 1992

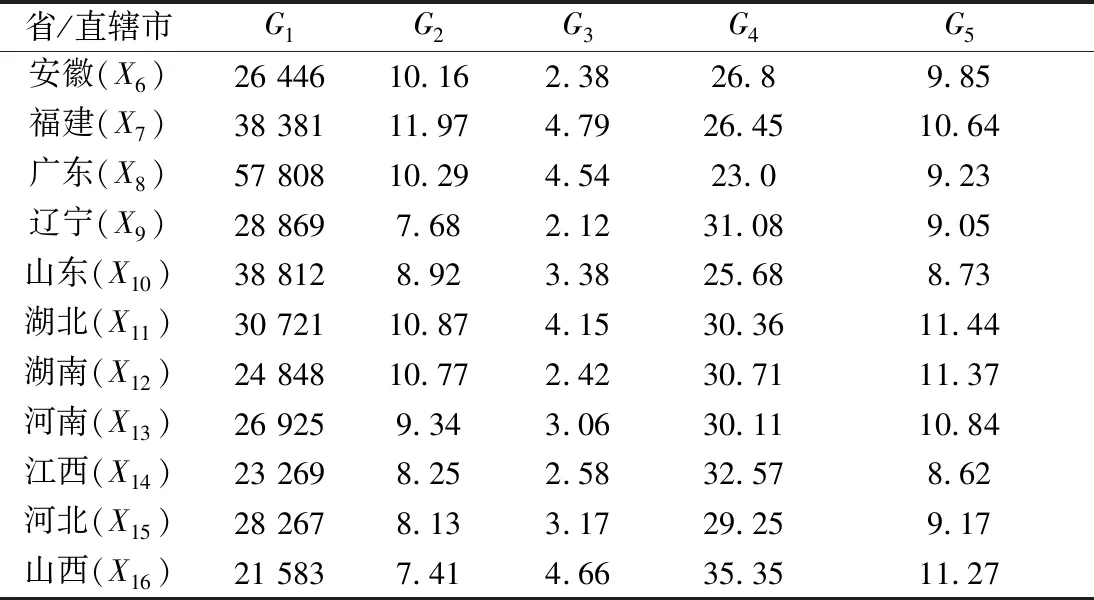
续表1Continued Table 1

已知方案集为={北京(),天津(),上海(),…,山西()},属性集为

式中:是成本型属性,其余均为效益性属性。各属性权向量为

=(0229 6,0187 6,0155 7,0265 6,0161 4)

下面利用本文提出的多属性相似度一致性投影决策法进行分析,计算步骤如下:

得到的决策矩阵如表1所示。

对不同的属性进行规范化处理得到规范后的决策矩阵(见表2)和理想决策向量。

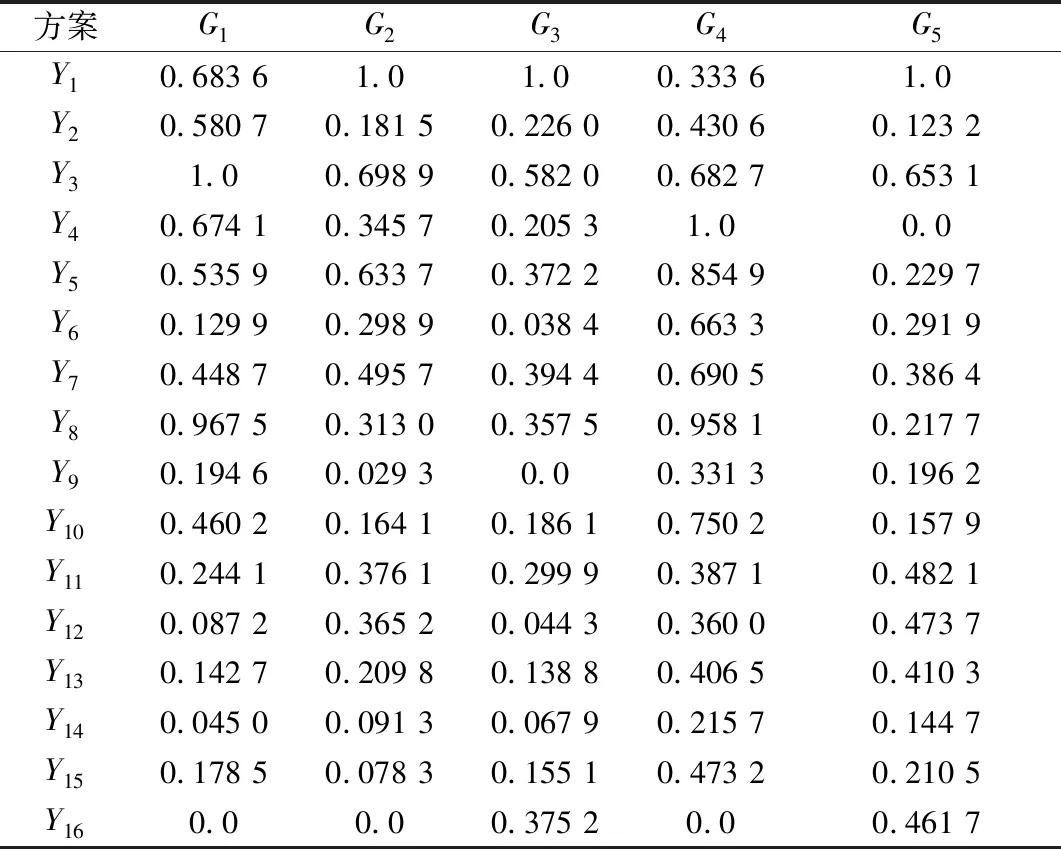
表2 规范化后的决策矩阵Table 2 Normalized decision matrix

根据表2得到理想决策向量为

由式(13)可得各个方案的理想偏移向量为

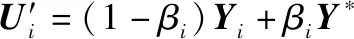
根据表2可得加权决策矩阵(见表3)和加权理想决策向量。

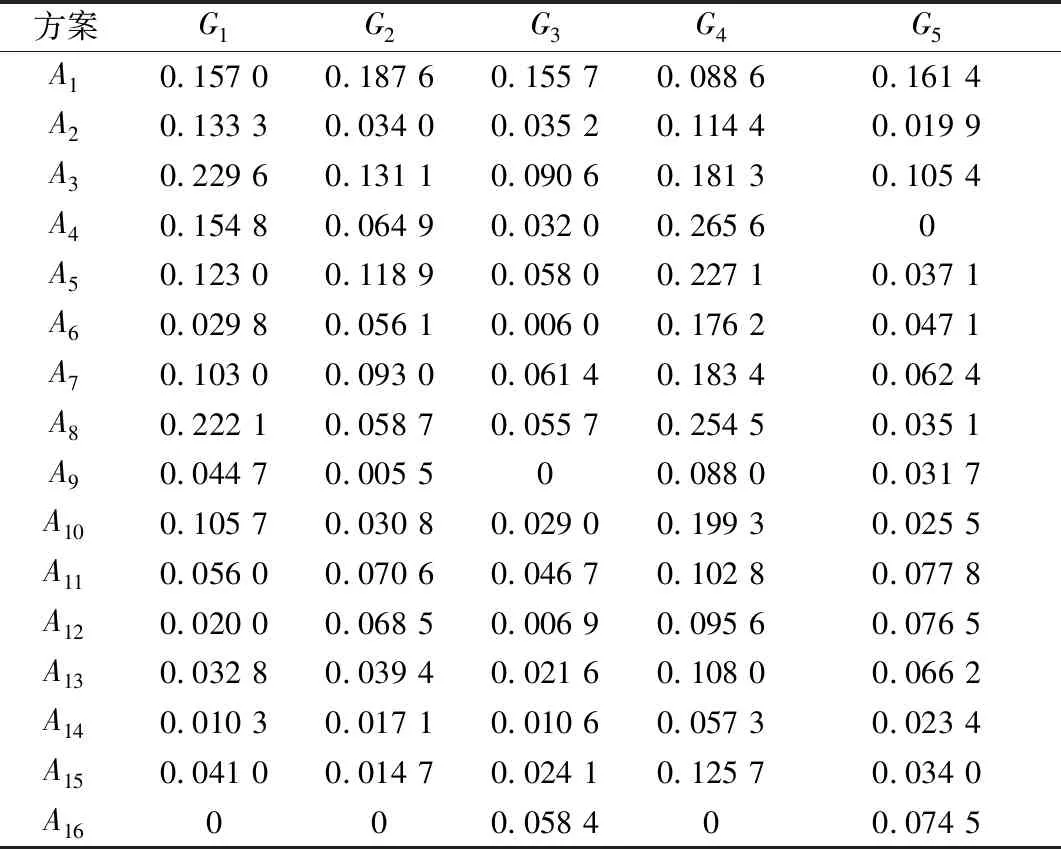
表3 加权决策矩阵Table 3 Weighted decision matrix

根据表3可得加权理想决策向量:

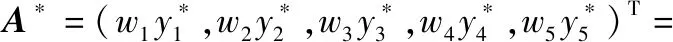
由式(13)可得各个方案的加权理想偏移向量为

=(1-)+

根据决策者的偏好确定偏好系数,不妨取偏好系数=12。

计算各个方案的综合评价值。

在偏好系数=12下,本文提出方法的综合评价函数可表示为

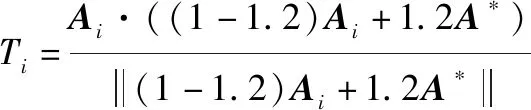
从而可得各方案综合评价值,如表4所示。

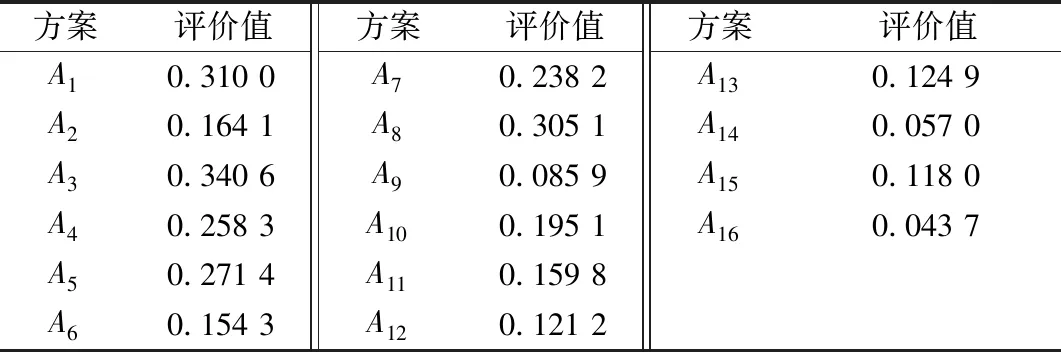
表4 各方案的综合评价值Table 4 Comprehensive evaluation value of each scheme

由综合评价值可知>>>>>>>>>>>>>>>,则在偏好系数的综合评价标准下,最佳方案是()。

4.2 不同偏好系数下的综合评价值

为了进一步说明本文得到的排序在均衡考虑决策向量与理想向量接近程度的关键因素方面哪个更合理,根据表3计算了方案在不同偏好系数下的综合评价值,如图6所示。

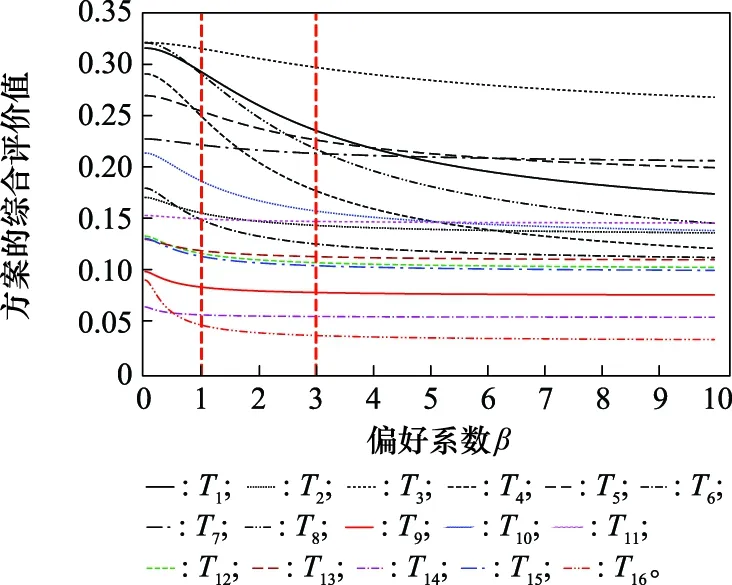
图6 方案在不同偏好系数β的情况下的综合评价值Fig.6 Comprehensive evaluation value of the scheme under different preference coefficients β

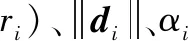
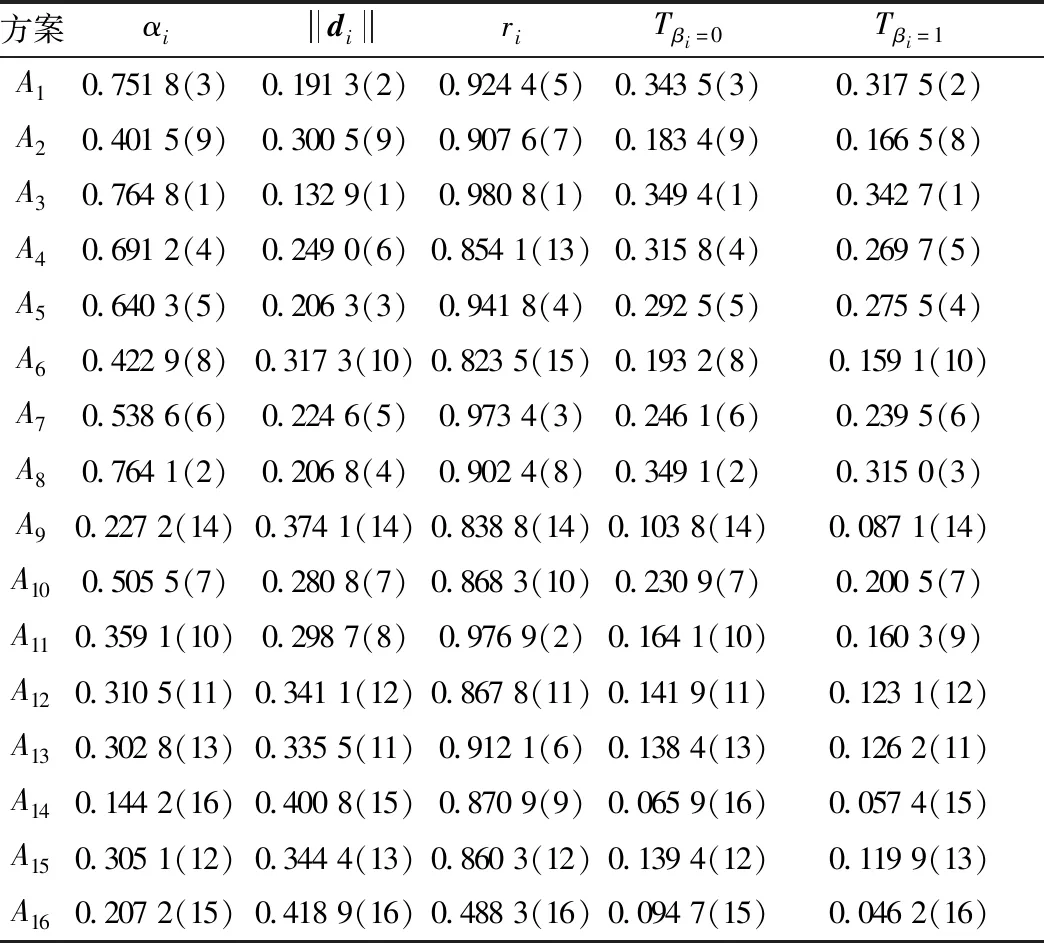
表5 按照单一相似度排序Table 5 Sort by single similarity

首先,从图6和表5可以看出,当增加时,方案与方案之间的相对位置变化稳定,这表明相应相似度的权重缓慢变化。

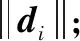
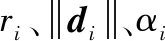
最后,综合图6和表5还可以看出,方案3(上海)与方案9(辽宁)的相对位置不发生变化,体现了所提方法不因偏好系数的变化而影响绝对优势、相对优势(上海、辽宁)和绝对劣势的客观评价,本文的方法保留了相似度之间的客观优势。

4.3 算例结果的比较分析

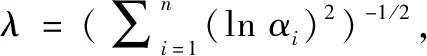
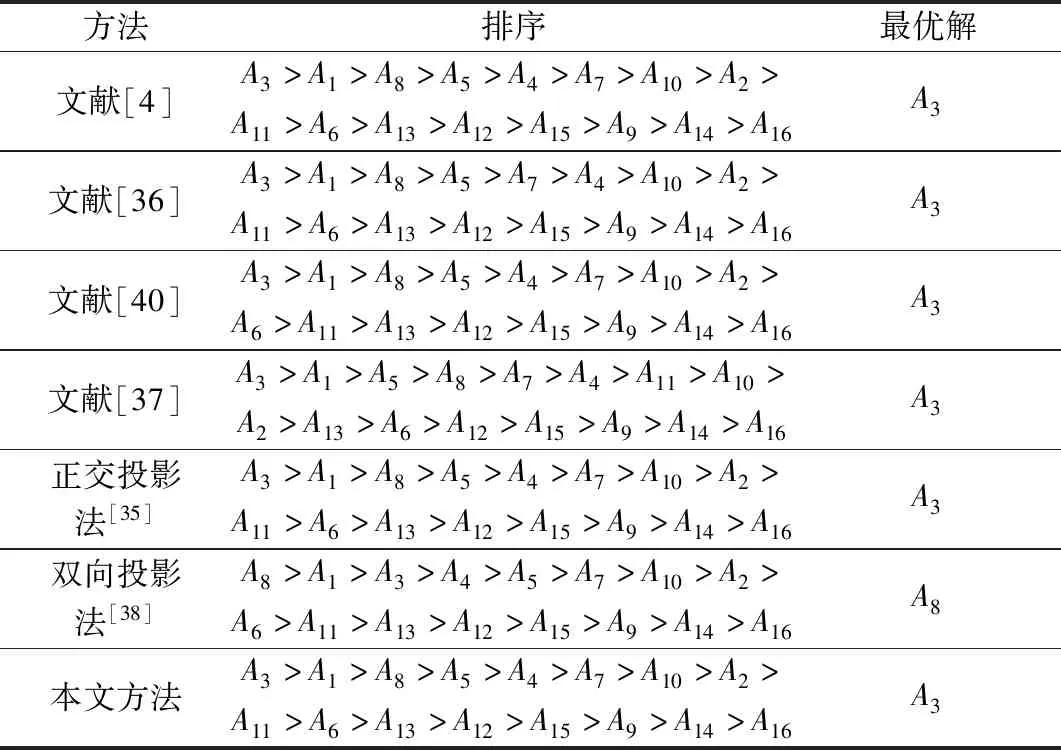
表6 7种方法的决策结果比较Table 6 Comparison of decision results of seven methods

通过表6可以看出,除了采用双向投影法外,是最好的方案,是最差的方案。

综合表4、表5和图6,为了避免重复表述,下面对文献[4,36,40]的方法与本文方法得到的排序结果进行比较分析。

本文与文献[4]所提方法的排序结果相同,这验证了本文方法的有效性。同时,本文取=12的式(14)提高了距离相似度和方向相似度的权重,降低了模相似度的权重,从而导致的值发生变化。同理,当偏好系数∈[097,15]时,其排序结果与文献[4]相同;当偏好系数∈[17,18]时,其排序结果与文献[36]相同;当偏好系数∈[09,095]时,其排序结果与文献[40]相同。这进一步表明所提方法综合考虑了模相似度、距离相似度、投影的一致性。

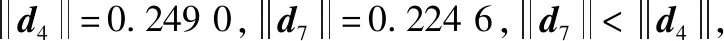
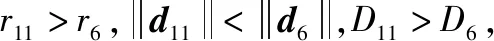
综上所述,本文所提方法主要有以下几方面的优势:

(1) 综合考虑了4种相似度,能避免单一相似度的不全面和综合评价函数的失效;

(2) 评价函数相比文献[36,40]更简单,当备选方案和属性个数较多时,该优势将会体现得更加明显;

(3) 考虑到主观因素对理想向量的调整;

(4) 有利于融入决策者的偏好,还有利于评价数据的评价标准统一;

(5) 相似度之间的客观优势不随偏好系数的变化而改变,能一定程度上限制决策者的随意性,更好地发挥决策者的主观能动性,体现了在复杂环境下主观与客观评价相互有益的补充。

5 结 论

本文给出了多属性决策与评价的新方法——相似度一致性的投影决策法,并对现有相关方法进行了梳理和评价。然而,本文给出的理想偏移向量容易受到决策者之间偏好的影响,如何综合所有的评价数据拟合一条稳定的理想偏移曲线值得考虑。对于高维空间数据映射到平面空间进行评价可能存在信息重叠的现象,不仅要考虑决策者的标准偏好,还要考虑与具体目标结合建立数学规划模型,才可能避免高维曲线这类问题。在影响决策者偏好因素方面,还需要进一步的研究。

随着其他理论的多元发展,结合本文提出的方法,对于不同的数据类型,决策规则更加多样;对于不同评价数据分布,评价角度更加灵活。还需要指出的是,本文的方法与密度中间算子结合,在决策的两个层面表达了决策者的标准一致性和群体评价意见偏向,更有利于决策者精细化的表达,这可能会促使群决策问题新的思考。