基于频域稀疏压缩感知的雷达目标三维散射中心反演方法

田 鹤, 董纯柱, 殷红成

(北京环境特性研究所电磁散射重点实验室, 北京 100854)

0 引 言

基于平面阵列微波天线结构下的目标三维散射中心反演及三维成像技术已被广泛应用于安全检查、产品检测、生物医学成像等领域。当平面阵列中天线孔径均匀等间隔分布时,目标反演精度最优,但对应的数据计算量及复杂度亦随之增加。设计合理的稀疏采样方式以及稀疏重构算法,可在满足反演精度的同时大幅降低数据量需求。文献[9]针对机载阵列合成孔径雷达(synthetic aperture radar, SAR)以巴克码为准则实施稀疏重航过采样,使载机飞行次数减少50%。此方法使成像结果避免了图像栅瓣影响。针对副瓣噪声,文献[10]通过构造参考复图像信号,并利用两幅图像干涉和低通滤波处理,在频域去除图像副瓣影响,但此方法在消除噪声的同时也会损失图像细节。文献[11-12]在干涉处理的基础上,利用频域稀疏特性,引入压缩感知(compressed sensing, CS)理论实现了三维图像重建。在此基础上,文献[13]将主成分分析(principal component analysis, PCA)引入稀疏信号重建过程,通过对回波信号进行降维处理以去除由稀疏采样带来的副瓣噪声和高频噪声。

针对上述研究背景,本文提出一种基于频域PCA和CS的稀疏微波三维散射中心反演方法。以组合巴克码作为稀疏采样准则,利用PCA对稀疏频谱的二阶统计量进行特征提取,去除稀疏采样带来的噪声影响。基于干涉原理,构建稀疏采样下的目标散射中心反演模型,建立基于CS的最优化问题并进行优化求解,以获得目标散射中心幅度和三维空间分布。

1 观测模型

基于平面阵列微波天线结构的目标观测几何模型如图1所示。以目标场景中心为原点建立直角坐标系,坐标系中天线孔径形成的阵列平面为-平面,天线照射方向(平行于观测目标的高度方向)为方向,也称距离向。各天线孔径通过时分方式依次发射并接收宽带信号,形成的采样平面大小为×,采样间隔为,场景中心到采样平面的距离为。本文选择方向作为稀疏采样方向,在选择稀疏采样方式时,考虑到巴克码伪随机序列具有约50%的占空比和良好的自相关特性,但巴克码的码长最长只有13位,故本文采用组合巴克码作为稀疏准则。组合巴克码伪随机序列的相关特性略差,但码长较长。利用4位巴克码[1110]和11位巴克码[11100010010]可构成一列组合巴克码序列,该编码序列为[1110111011100001000100011110000100011110000],长度为44,稀疏率约为50%。从图2可知,该组合巴克码自相关图较为尖锐(见图2(a)),说明其具备一定的随机性,且天线方向图(见图2(b))中远区副瓣较低,可以应用于微波三维成像观测。

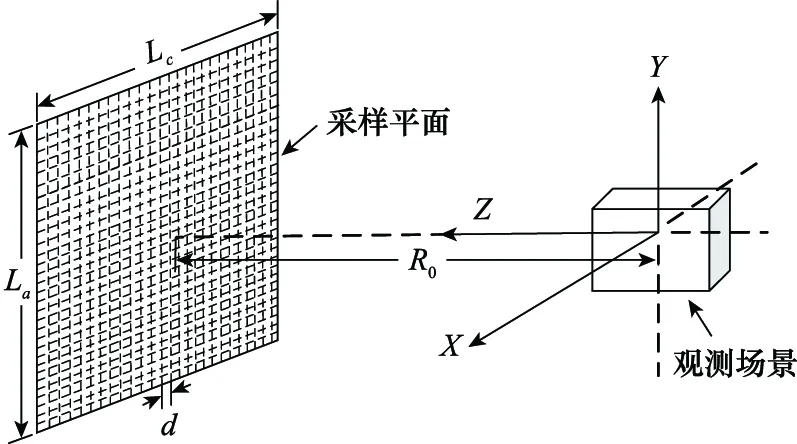
图1 基于平面阵列微波天线结构的目标观测几何模型Fig.1 Geometric model of target observation based on planar array and microwave antenna structure

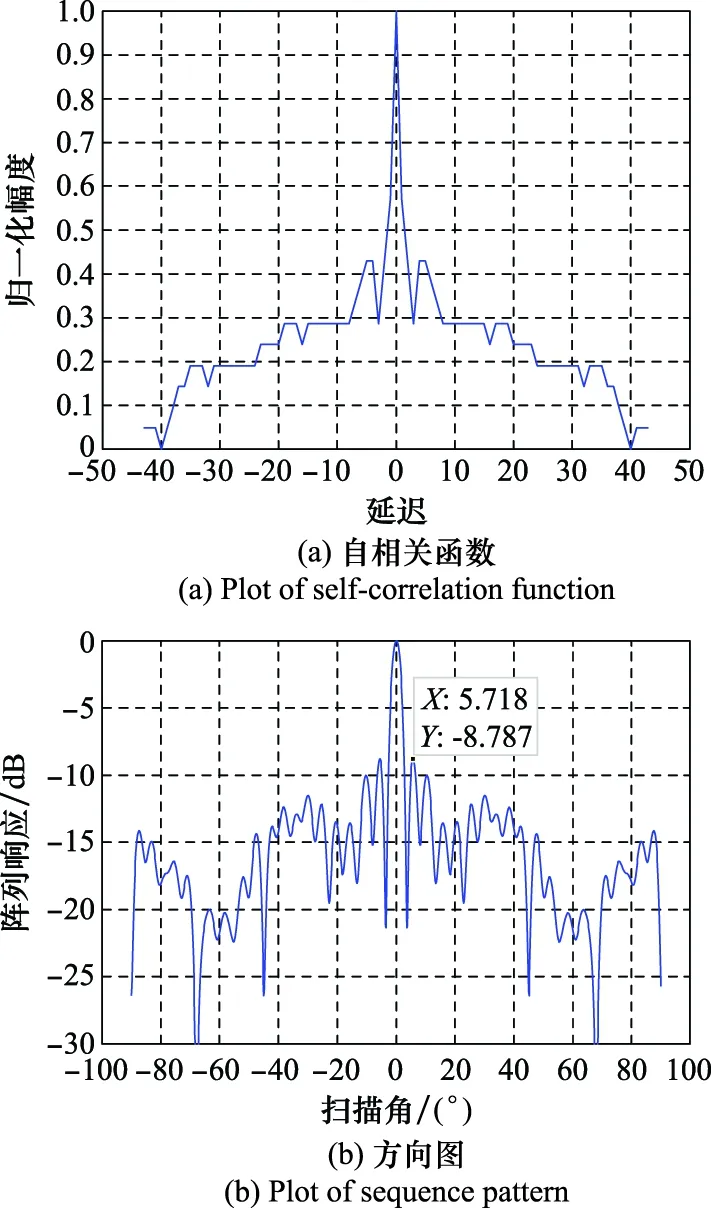
图2 44位组合巴克码自相关与方向图情况Fig.2 Plot of self-correlation and antenna pattern for 44 combined Barker sequence

2 基于频域PCA和CS的重构算法

2.1 频域PCA构造参考信号

可通过正交变换减少PCA的数据维度,保持数据中方差贡献最大的特征,在对原始复杂数据降维的同时,去除由稀疏采样带来的噪声泄露。

已知回波频谱对应的傅里叶基为正交基矩阵,这与PCA对输入数据属于正交空间的要求相一致。假设稀疏采样回波经过三维匹配滤波(脉冲压缩)处理得到的粗聚焦结果为,为三维复数矩阵,对应的三维频谱为,则在方向中第(1≤≤,为距离向分辨单元总数)个距离频率处的二维频谱为

(1)

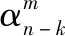
假设在方向不同频率间的协方差矩阵为,∈×,中第(,)个元素为

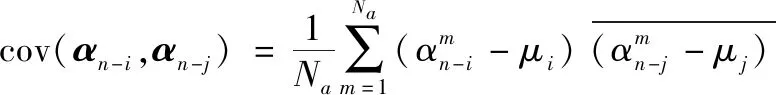
(2)

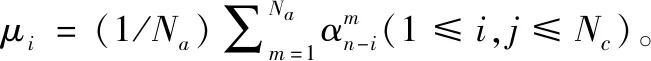
=diag{,,…,,…,}

(3)

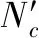
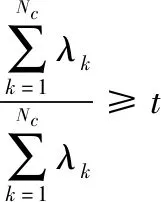
(4)

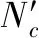
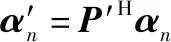
(5)

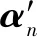
=IDFT{′′}

(6)

本文将该结果作为后续干涉处理所用的参考复数信号。由于数值小的特征值所对应的特征向量往往与噪声有关,因此可认为重建后的粗聚焦结果具有抑制稀疏采样副瓣噪声的性能。

2.2 频域CS重建散射中心

根据CS理论,不完备采样下信号被正确重建的前提为信号存在稀疏表征。当微波观测目标在空间为连续分布时,其对应的回波信号不满足空间稀疏特性,且成像分辨单元内存在随机初始相位,对应的频谱信号也不满足频域稀疏特性。在此考虑利用干涉处理去除微波复图像的随机初始相位,使信号在频域具备稀疏性质。其中,干涉所用的参考复数信号由频域PCA方法重构而成。

假设待重建的目标散射中心三维复数矩阵为,对应的三维频谱为,两者关系为

=

(7)

式中:为逆傅里叶基。假设频域PCA构造的参考复数信号为,对和进行干涉处理,得到干涉后的三维复数矩阵:

=||·exp{j[∠()-∠()]}

(8)

由于和对应的天线视角相同,随机初始相位近似相等,故相位中已去除随机初始相位的大部分影响。假设对应的频谱为:

=

(9)

则具备稀疏性,可在频域引入CS理论进行频谱系数求解,并反变换至图像域,可获得目标散射中心幅度和三维空间分布。频域线性测量矩阵建立的过程为:假设图1中阵列平面内某一采样点的空间位置为(,,),其中1≤≤;设目标区域中的某一散射中心的空间位置为(,,),其中1≤≤,为方向(稀疏方向)目标散射中心分辨单元总数。根据几何光学理论和线性近似,经过、方向二维匹配滤波后的离散回波信号为

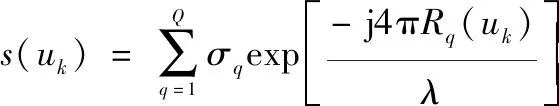
(10)

式中:()为空间采样点到目标区域中该散射中心的往返距离:

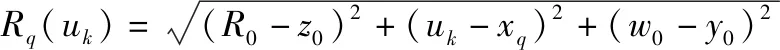
其中,为该点对应的散射系数。

将()进行泰勒级数展开,得

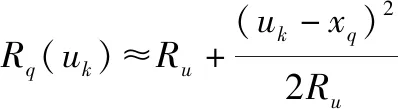
(11)

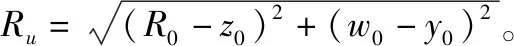
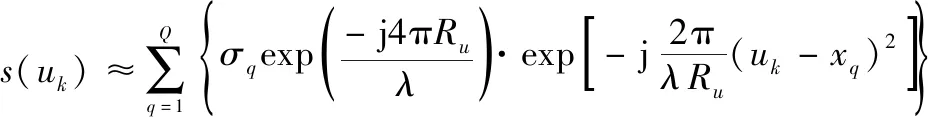
(12)

将()重新写成如下向量相乘的形式:

()=(:,,)

(13)

式(13)即为交轨向第个回波信号的一维线性测量模型;为基向量,大小为1×,第个元素为

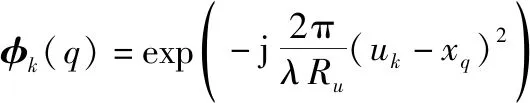
(14)

(:,,)为散射系数向量,大小为×1,第个元素为

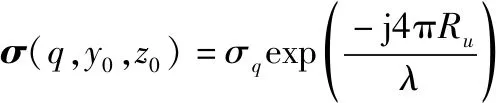
(15)

为便于表达,在后续分析中将(:,,)简写为。可将测量模型表示成矩阵形式:

=

(16)

式中:=[();();…;()]×1;=[;;…;]×;为由稀疏采样准则决定的选择矩阵。根据上述分析可知,用于求解图像稀疏频谱的距离频域CS测量模型可写为

=exp[j∠()]=exp[j∠()]

(17)

可根据式(18)所示的优化准则求解方向频谱,以实现对目标散射中心的三维位置分布重建,获取目标高精度几何尺寸信息。

(18)

3 暗室试验处理

在暗室试验中,观测目标为一辆坦克模型。为了体现观测目标的空间不稀疏性,在坦克模型外部涂覆了锡箔层,并以金属板作为背景(金属板上粘贴树叶),如图3所示。天线以图1所示的平面阵列结构进行数据获取,发射信号为步进频率信号。试验参数如表1所示。

图3 暗室观测目标Fig.3 Experimental target of the anechoic chamber

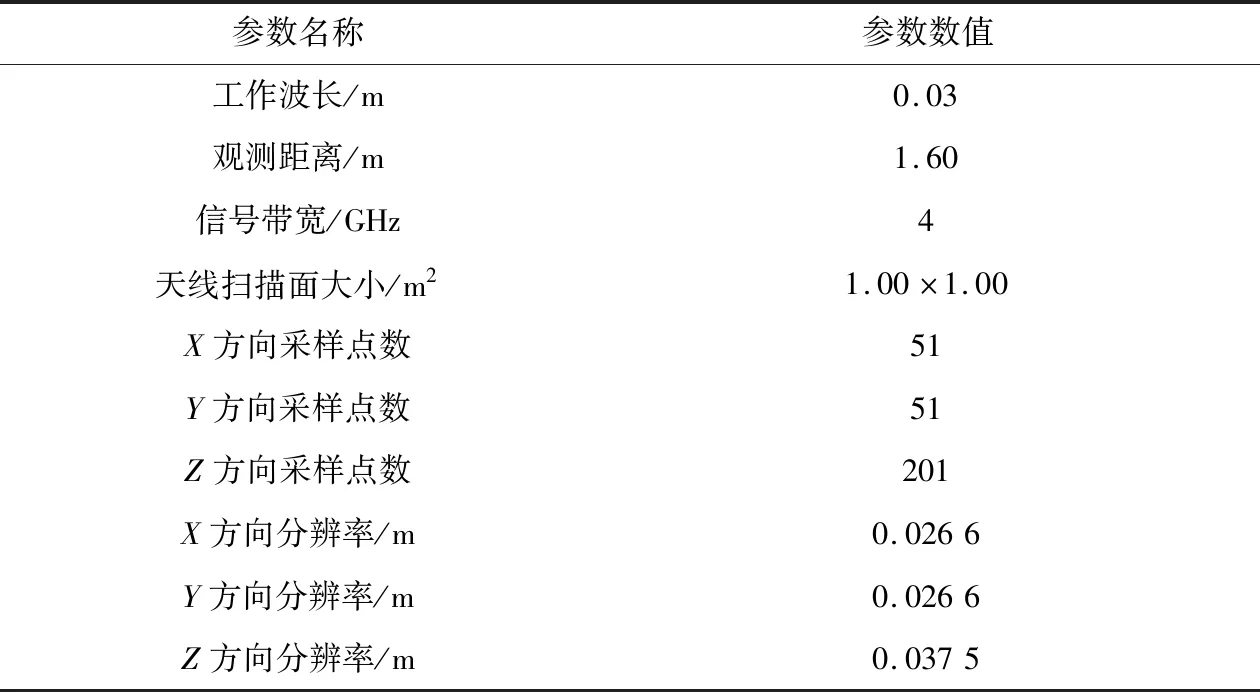
表1 试验参数Table 1 Experimental parameters

完备采样下回波的三维匹配滤波结果如图4所示,其中图4(a)为目标散射中心三维复数数组在距离向1.3 m处对应的-截面图,表示该距离下的散射中心幅度值(单位: dB);图4(b)为目标散射中心方向位置对应的等高线图,表示各散射点在目标中的相对高度;图4(c)为重构的散射中心三维位置分布点图,表示各散射中心的三维位置分布。由于缺乏理论值,本文在后续重构性能评价中,将图4所示结果作为真值进行量化误差分析。

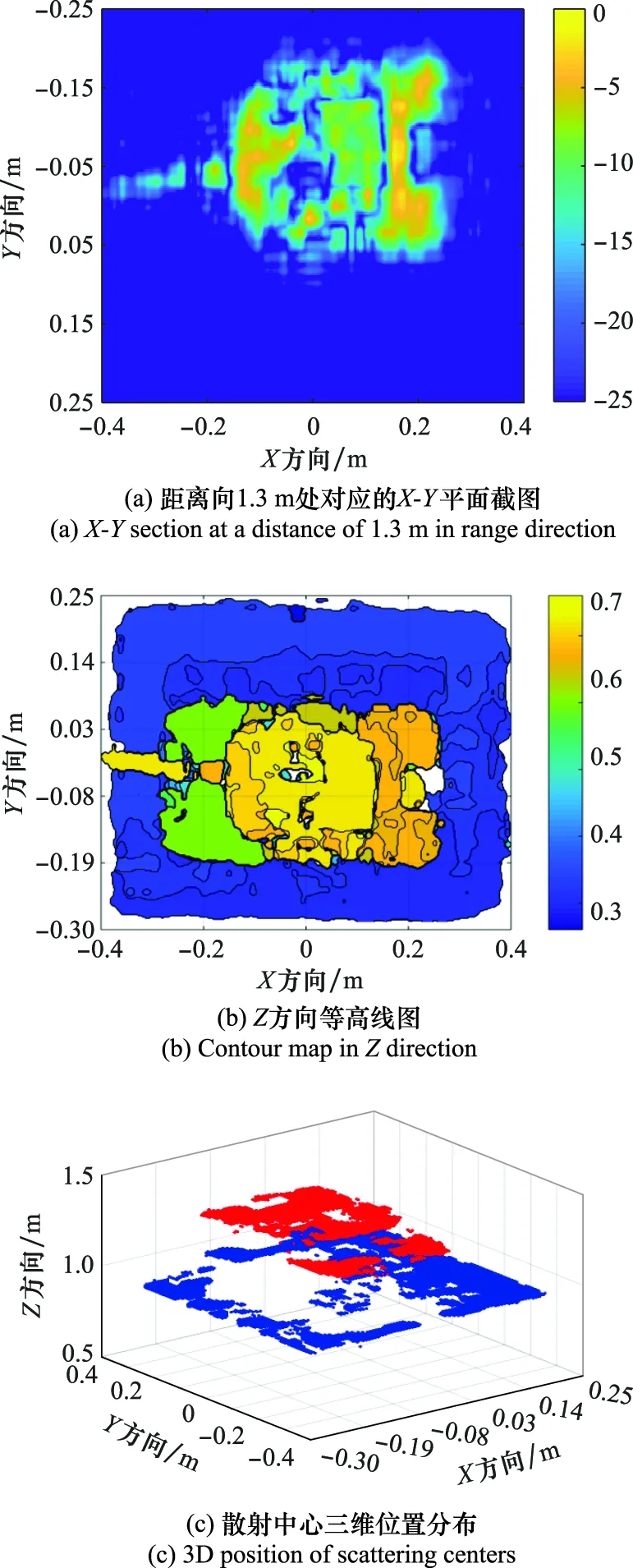
图4 完备采样下微波回波直接匹配滤波结果Fig.4 Results of microwave echo match filtering method under complete sampling

按照组合巴克码进行稀疏采样,获得的三维匹配滤波结果如图5所示。从图5可看出,在稀疏采样率为50%的条件下,组合巴克码稀疏采样方式能够避免部分栅瓣影响,但仍然存在较严重的副瓣能量泄露,需要进行算法重构。

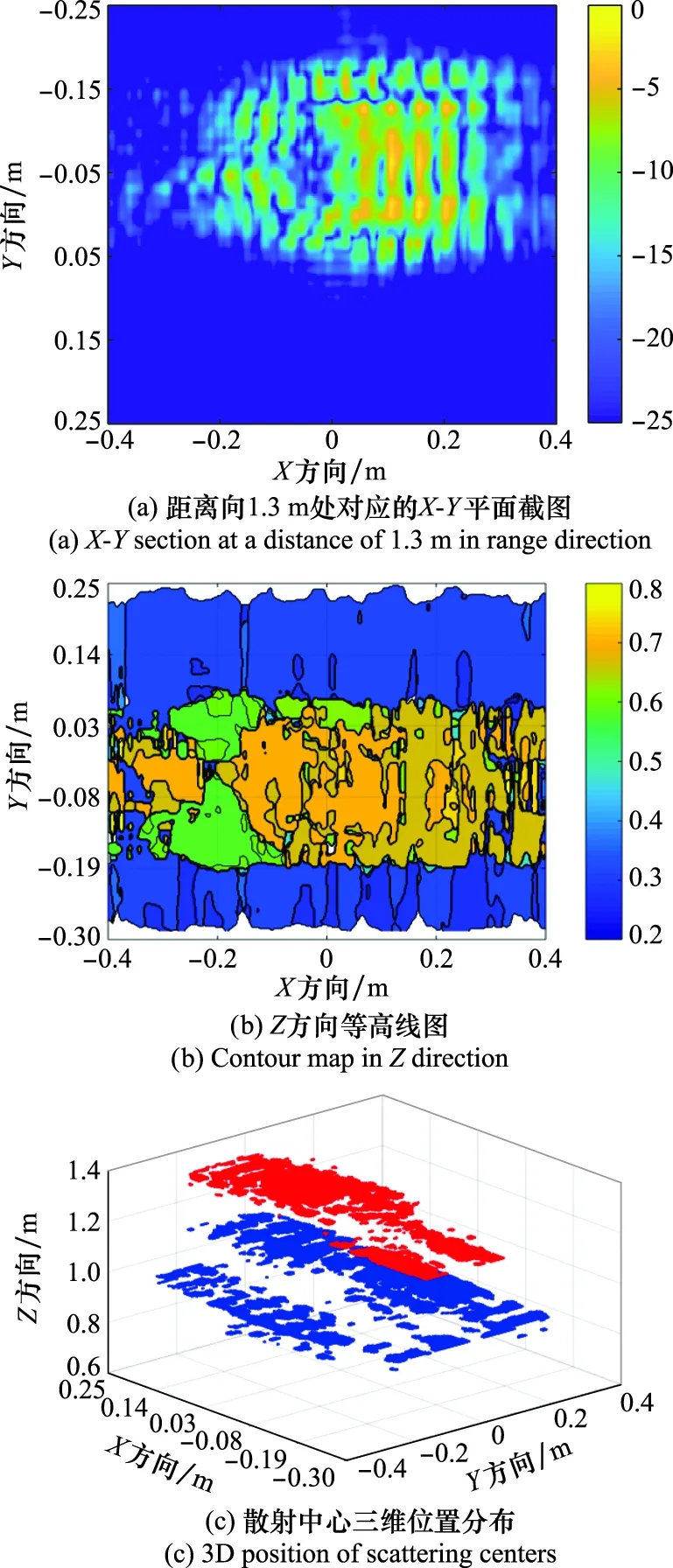
图5 稀疏采样下微波回波直接匹配滤波结果Fig.5 Results of microwave echo match filtering method under sparse sampling

利用PCA在频域对稀疏采样回波进行PCA,获得的参考复数图像如图6所示。图6中,目标散射中心重构结果消除了高频副瓣噪声,但由于频域PCA降维处理,图像高频细节有所缺失。在此基础上,利用PCA得到的参考信号与原始稀疏回波对应的复数图像进行干涉处理,干涉处理前后的信号三维频谱如图7所示。从图7可以看出,经过干涉处理后的信号频谱具备稀疏表征,为后续CS稀疏信号重建提供了充分条件。在此基础上利用式(18)对稀疏频谱进行重建,并反变换至空间域,得到目标的散射中心三维分布,如图8所示。从图8可以看出,基于频域CS的三维重建算法能有效抑制由稀疏采样带来的副瓣噪声和高频噪声,可正确重建出目标在三维方向的散射点位置,同时较好地保留了观测目标的细节和连续性。

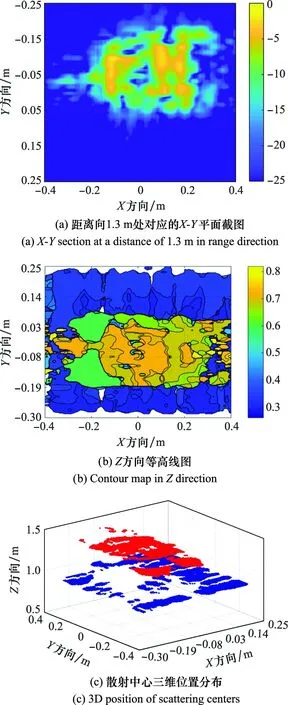
图6 稀疏采样下频域PCA对应的参考复数图像结果Fig.6 Referential complex images of PCA in frequency domain under sparse sampling

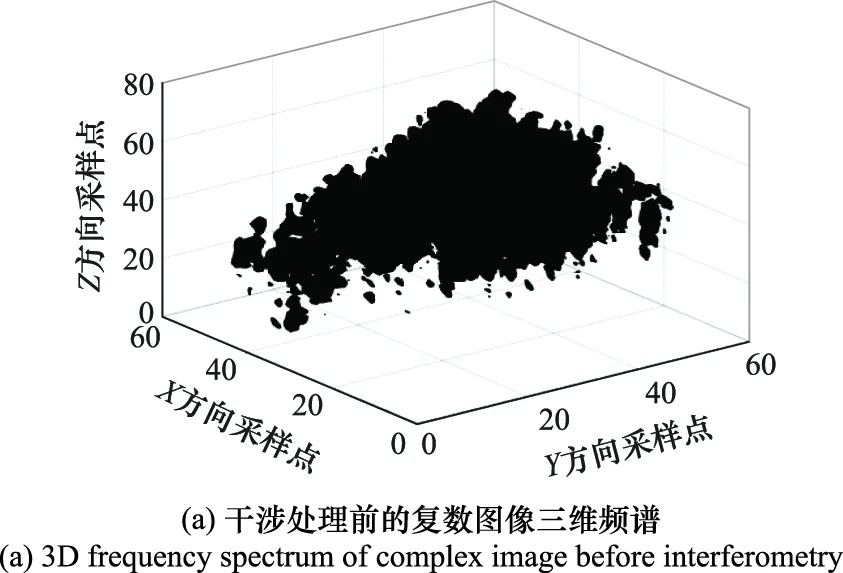
图7 稀疏采样下干涉前后的复数图像三维频谱Fig.7 3D frequency spectrum of complex images before and after interferometry under spares sampling

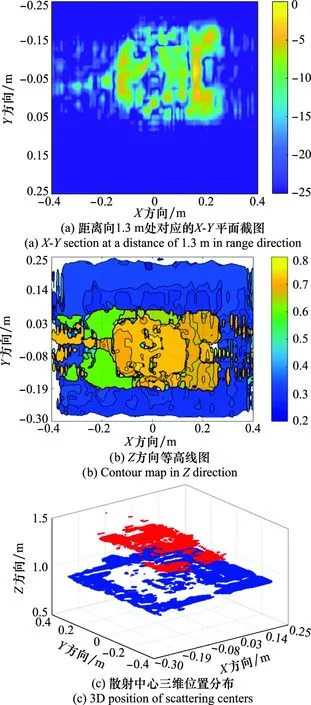
图8 稀疏采样下频域CS重建结果Fig.8 Reconstructed results based on CS in frequency domain under sparse sampling

在稀疏重建结果定量评价过程中,采用相关系数、均方根误差(root mean square error, RMSE)和结构相似度(structural similarity index, SSIM)作为指标,评价对象为重建前后的目标各散射点幅度和位置形成的三维复数矩阵,表2为组合巴克码稀疏采样条件下不同算法得到的图像质量评价结果。在定量评价分析中,文献[8]提出的频域CS重建算法和文献[9]提出的频域低通滤波(low pass filtering, LPF)算法的相应结果也用来进行对比。从表2结果可知,基于本文所提的频域稀疏CS反演方法得到的散射中心位置分布及幅度反演结果RMSE最低,且与完备采样结果的相关系数和相似度最高,验证了上文理论和数据分析。

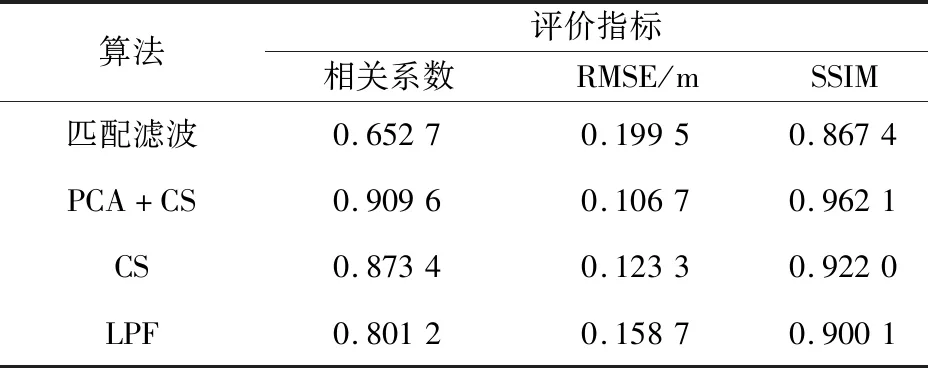
表2 算法重构性能评价Table 2 Reconstruction performance evaluation of different algorithms

4 结 论

本文以组合巴克码为准则实施稀疏采样,对应的孔径稀疏率为50%。提出一种基于频域PCA和CS的目标三维散射中心重构算法,利用PCA构造参考复数矩阵,并通过干涉处理使原始稀疏回波信号的三维频谱具备稀疏性。由于干涉处理后复图像频谱集中,因此可基于CS对频谱建立线性观测矩阵,并进行最优化求解,获得待重构三维散射中心对应频谱,进而实现稀疏采样下的微波散射中心三维位置的精确重建。暗室试验结果表明,在组合巴克码稀疏采样条件下,该算法可获得与完备采样相近的重构质量。

本文所提的频域稀疏CS雷达目标三维散射中心反演方法可应用于人体安检、对地侦察等热门领域,并为目标三维特征提取及识别应用提供技术支撑。