基于数据场联合决策图改进的GMM聚类

王 磊, 张志勇, 曾维贵, 曹司磊, 张天赫

(1. 海军航空大学岸防兵学院, 山东 烟台 264001; 2. 中国人民解放军91827部队, 山东 威海 264000)

0 引 言

雷达信号侦察作为电子侦察的重要组成,指通过对侦收到的雷达信号进行参数测量、聚类分选等,进而实现对雷达辐射源目标的定位、识别和威胁判定。随着电子信息技术的不断发展,战场电磁环境变得更加复杂多变,同一空间中雷达辐射源数量猛增、雷达信号形式变得更加复杂多样、混合信号在参数空间交叠严重以及杂波干扰等问题对雷达信号分类提出了严峻挑战。

为了解决雷达信号分类面临的问题,近年来国内外研究者针对无监督聚类提出了一些系列新算法或改进措施。李德毅院士2006年首次将物理世界中场的概念引入到数据处理领域,创造性地提出了数据场理论,因其可自动确定聚类中心和聚类数目的优点,为雷达信号分类处理提供了一种新思路。针对K-means算法需要预先设定聚类中心和聚类数目的缺点,赵喜贵等将数据场引入到雷达信号分选,并与K-means算法结合提出一种融合算法,提高了在缺少先验知识的情况下处理未知雷达信号的能力。张怡霄等提出将数据场与脉冲重复间隔(pulse repetition interval, PRI)变换相结合,根据PRI估值结果对待分类脉冲进行预分选和类中心合并,自动得到K-means初始聚类中心和聚类数目,在一定程度上改善了K-means算法的局限性,但存在相关参数设置复杂等问题,且仍存在对非球体数据对象聚类效果差的问题。沙作金将数据场与平面变换算法相结合,提升了复杂电磁环境下的雷达信号分选能力。后来郜丽鹏和沙作金又针对数据场聚类在雷达信号分类中的应用对场强函数做了改进,提高了算法对孤立噪声脉冲的抗干扰能力。2014年Rodriguez 等在Science上发表了一种快速搜索密度峰值聚类(clustering by fast search and find of density peaks, CFSFDP)方法,在人工参与的情况下借助密度距离决策图可以快速确定聚类中心和聚类数目,具有计算速度快等优点,但缺点也很明显,即需要人为参与,自主性有待提高。Zhu等针对CFSFDP方法需要手动设置簇中心和截断距离的问题,提出利用粒子群优化算法自动确定聚类中心和截止距离,并成功应用于提高癌症预测准确率。Li等提出了一种阈值曲线自确定方法,利用阈值曲线对决策图进行划分,实现对聚类中心和聚类数目的自确定,并将改进的CFSFDP方法应用于雷达信号分选,无需设定任何参数,自动实现了对待分类数据聚类分选,但算法对孤立噪声脉冲干扰较敏感。

现代电子侦察设备侦收到的雷达信号参数错综复杂且密集程度高,要求分选算法具备抗干扰能力强、人为依赖性低、处理时效性高等能力。传统常用于雷达信号的聚类分选方法如K-means、模糊C均值、基于密度的噪声应用空间聚类(density-based spatial clustering of applications with noise, DBSCAN)、高斯混合模型(Gaussian mixture model, GMM)等算法,不同程度存在适用范围窄、抗干扰能力弱、需要人为设置参数、计算复杂度高等问题。上述提到的部分改进方法,往往针对聚类算法的某一方面进行改进,在复杂环境下处理雷达信号分选时,依然存在不少问题。为此,本文提出一种基于数据场联合决策图改进的GMM聚类算法,通过累加数据对象场强函数值形成数据势能,根据孤立点势能明显低于目标区域的特征对孤立点进行剔除。该方法借鉴密度峰值聚类中决策图的思想,根据数据对象势能与其到达最近大势能点之间的距离构建势能-距离决策图,通过势能距离积下降率确定边界点,来自动确定聚类中心和聚类数目,最后通过GMM聚类算法完成数据对象的聚类分选。

本文结构安排如下:第一部分介绍了数据场聚类原理及其相关改进;第二部分介绍了决策图的基本思想、聚类中心点和聚类数目的自确定方法;第三部分对现有算法进行改进,并就总体实现方式进行了介绍;第四部分对本文方法就聚类准确度、算法鲁棒性、时间复杂度等方面进行了仿真对比;最后进行了总结分析。

1 数据场理论

“场”是一种描述事物之间相互作用的概念,现实生活中广泛存在着各种场,如电场、磁场、引力场等。在数据场中,数据对象的势能正比于该对象所处空间位置的场强,受空间中所有数据对象的辐射场强共同作用决定。数据场中数据对象之间的作用力类似库仑力,距离越近作用力越大,距离越远作用力越小,所有数据对象之间的作用力和作用范围共同构成了整个数据空间的数据场。

1.1 场强函数

类似于电场和引力场,场强函数被定义为用于描述数据对象对其他数据对象作用能力的概念,位于数据对象附近的空间中由该对象产生的数据场场强较大,相反距该数据对象较远的空间中由该对象产生的数据场场强较小。场强函数一般用高斯函数表示,定义数据空间中数据对象在数据对象处产生的数据场场强为

(,)=·exp[-(,)·(2)]

(1)

式中:为数据对象的影响因子,类似于引力场中物体的质量、电场中物体带电量等属性,鉴于数据场中各数据对象的独立性和完备性,一般将影响因子设为1;(·)为欧式距离函数;为描述数据对象间辐射作用能力的辐射因子。从数据场场强公式可以看出,辐射因子越大,数据对象对外辐射能力越强。

设定影响因子为1,则数据空间中数据对象受到来自数据对象的辐射作用可以表示为

(,)=·exp[-(,)·(2)]=
exp[-(,)·(2)]

(2)

1.2 势函数

数据场中数据对象所受的所有辐射作用的标量和定义为该数据对象的势函数,其数值称为数据对象的势能。假设数据空间中存在个数据对象,,…,,数据对象的势函数可以表示为

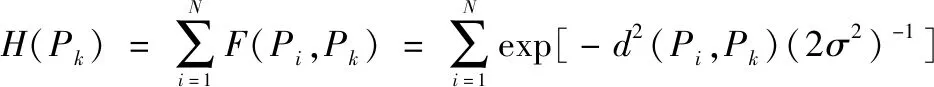
(3)

1.3 辐射因子

辐射因子是描述数据对象对外辐射能力的参数,单个数据对象在不同辐射因子设定情况下的场强函数如图1所示。

图1 不同辐射因子下场强函数曲线Fig.1 Curves of field intensity function under different radiation factors

场强随距离增大整体呈下降趋势,在辐射因子设置较小时,场强随距离下降较快,在辐射因子设置较大时,场强随距离下降较慢,辐射因子设定是否合理直接影响数据场聚类效果。为了提高数据场聚类算法的适应能力和聚类效果,减少对人为设定参数的依赖,后续需对辐射因子的选取方法进行改进,根据数据对象分布情况自动确定最优辐射因子。

2 决策图理论

传统的基于划分的聚类需要提前设定聚类中心和聚类数目,再通过不断的迭代运算调整聚类中心和数据对象的划分,最后达到设定条件下的最优。而决策图方法根据数据对象局部密度值与该对象到最近大密度点的距离构成密度-距离决策图,根据决策图中数据对象的分布实现快速确定聚类中心和聚类数目,故该算法又称为决策图聚类。

决策图思想基于两点基本假设:一是聚类簇中聚类中心是该簇中局部密度最大的数据对象;二是不同聚类簇对应的聚类中心之间相距较远。基于以上两点假设,在决策图中引入局部密度和最近大密度点距离的概念。根据决策图可以容易判定哪些数据对象是孤立噪声点,哪些数据对象是聚类中心点。即具有较小局部密度和较大最近大密度点距离的是孤立噪声点,具有较大局部密度和较大最近大密度点距离的是聚类中心点。

密度峰值聚类中数据对象对应的局部密度定义为

(4)

式中:局部密度表示在数据对象的邻域内存在的数据对象个数;为空间中数据对象个数;为截断距离,其作用与密度聚类中的邻域半径和数据场聚类中的辐射因子概念基本相同;阶跃函数定义如下:

(5)

该算法截断距离需要为人设置,且该参数设定的合适与否对聚类结果影响较大。

数据对象的最近大密度点距离定义如下:

(6)

即如果该数据对象的局部密度为全局最大,则其为与其相距最远的数据对象之间距离的一半,否则其为与比其局部密度高且距离最近的数据对象之间的距离。

根据各数据对象的局部密度和最近大密度点距离,生成密度-距离决策图,图2为密度峰值聚类中典型的决策图。从决策图右上角向左向下框选密度和距离较大的点,对应的数据对象即为聚类中心,进而依据距离最近原则将其他数据对象进行划分归类。

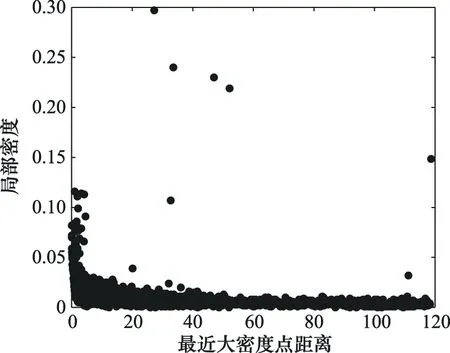
图2 典型决策图示意Fig.2 A typical decision diagram

3 算法改进

数据场聚类对于孤立噪声点不敏感,能够轻易发现并排除孤立点干扰,但后续聚类过程计算复杂度高;决策图是一种简单、快速寻找聚类中心点的方法,但易受孤立噪声点干扰。因此,本文拟结合数据场与决策图的优势,实现对孤立噪声点不敏感的快速聚类。根据数据场与决策图的基本原理易知,数据场中辐射因子参数需要人为设定且直接影响聚类效果,决策图中截断距离需要人为设定,聚类中心点需要根据决策图人为选取。为了提高算法自主程度,本文对以上问题提出如下改进。

3.1 辐射因子选取

(7)

假定数据空间中存在个数据对象,根据势熵表达式可知,当辐射因子取值非常小或非常大时,每个数据对象的势能均为1或均为,此时数据场中数据对象分布最均匀,对应的势熵取得最大值log。势熵En随辐射因子的变化趋势如图3所示,随着的增大,势熵先减小后增大。因此,辐射因子的寻优问题可以转换成势熵的最小值求解问题,即无约束一维极值问题,可用斐波那契法求解。

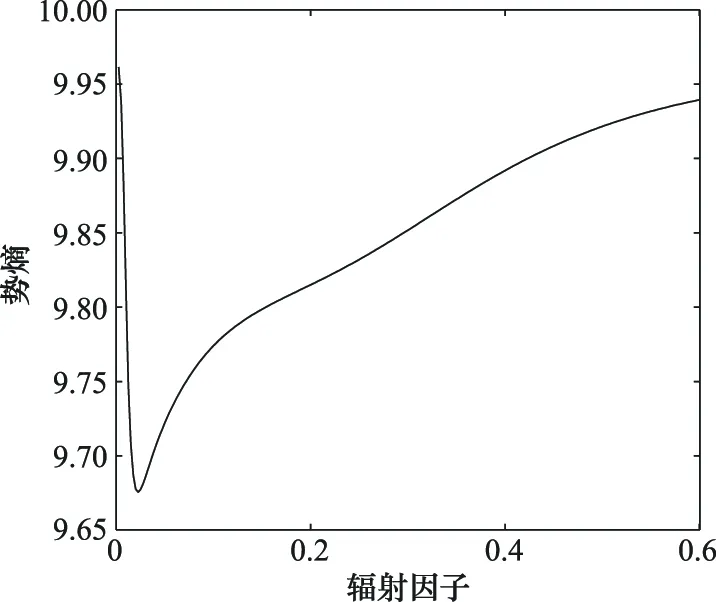
图3 势熵随辐射因子的变化趋势Fig.3 Variation of potential entropy with radiation factor

已知斐波那契数列可以表示为==1,=-1+-2(≥2)。根据一般经验,如数据空间中数据对象总数为,辐射因子的最优取值一般在10数量级,因此设定辐射因子的初始取值范围∈[0,100]。

利用斐波那契法对辐射因子进行最优逼近,算法流程如图4所示,进而得到满足设定精度要求的辐射因子参数。

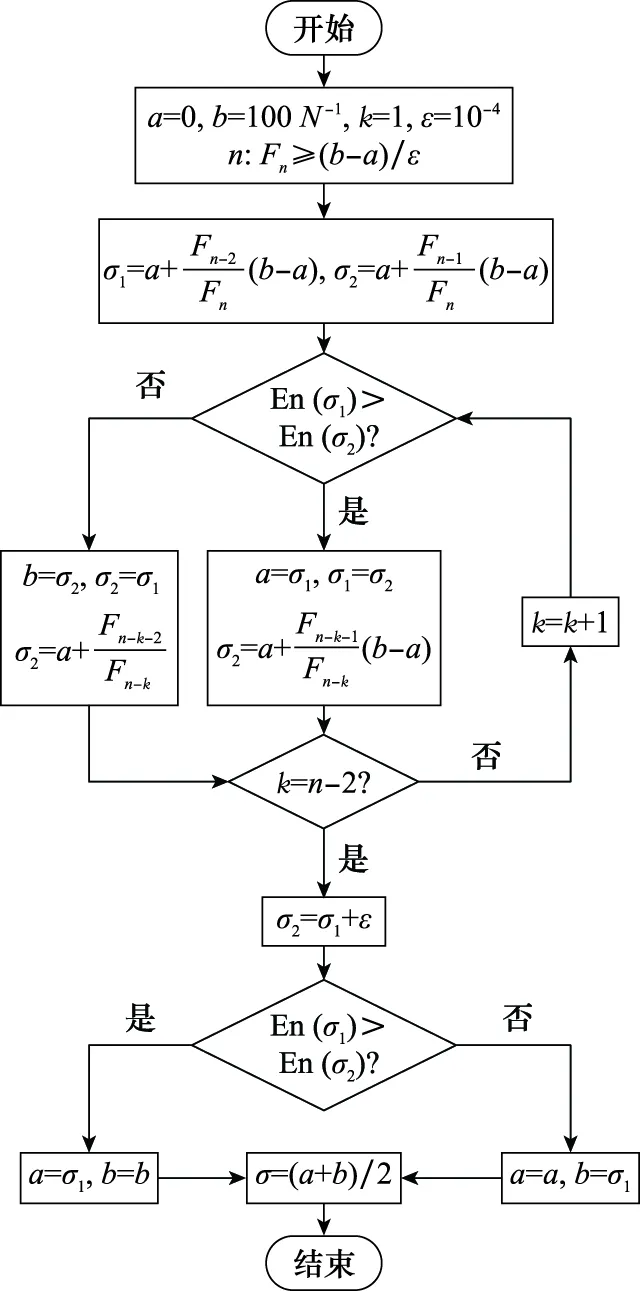
图4 辐射因子寻优算法流程图Fig.4 Flowsheet of radiation factor optimization algorithm

为了提高应对孤立噪声脉冲干扰的能力,对数据场中场强函数进行一定调整,使孤立噪声脉冲仅受自身辐射影响,进而方便利用势能值进行剔除。根据场强函数可知,在任意数据对象的[0,3]区间内包含了该数据辐射作用的9974%,因此为了降低聚类簇对孤立噪声的辐射作用,将数据点的场强函数改为

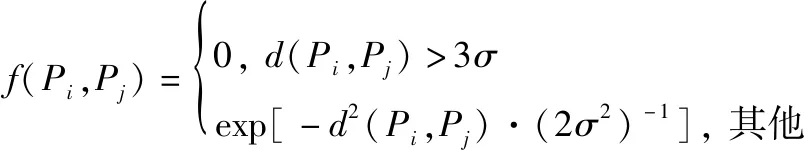
(8)

3.2 决策图改进

一方面,为了解决决策图对孤立噪声点敏感的问题,采用数据场中数据对象的势能代替决策图中的局部密度,构建势能-距离决策图,不仅避免了决策图中需要人为设定截断距离的缺点还提高了对孤立噪声点的处理能力。另一方面,根据决策图特点可知,聚类中心对应的势能和最近大势能点距离均较大,孤立噪声点势能较小而最近大势能点距离较大,聚类簇中除聚类中心点以外的其他点表现为势能较大而最近大势能点距离较小。因此,为了自动选择聚类中心,在决策图中引入势能距离积的概念,假定数据场中数据对象对应的势函数值为,最近大势能点距离(等同于最近大密度点距离概念)为,则该数据对象的势能距离积可表示为

=·

(9)

将所有数据对象按照势能距离积由大到小的顺序重新排列,图2中各数据点按照势能距离积重新排序后的势能距离积如图5所示,则势能距离积较大的前几个数据对象即为聚类中心。

图5 降序重排后的势能距离积Fig.5 Product of potential energy and distance after descending rearrangement

已知该决策图对应的原待分类数据包含7个聚类簇和一些孤立噪声点。由图6中势能距离积下降率易知,在根据势能距离积降序重排后的第7个数据对象对应的势能距离积下降率最大,依此设定第7个数据对象为聚类中心与其他数据对象的分界,即选择前7个数据对象为聚类中心,与原待分类数据真实分布情况相符。

图6 势能距离积下降率Fig.6 Descent rate of product of potential energy and distance

3.3 算法实现步骤

根据上述数据场联合决策图的方法,结合数据场对孤立噪声不敏感的特点及决策图在确定聚类中心方面的优势,完成对孤立噪声点的筛除、聚类数目和聚类中心的确定。然而在雷达信号分选应用中,由于不同属性参数在参数稳定性方面存在差异,该类参数分布不一致无法用归一化消除,会对最后的数据划分造成影响。如某部雷达信号所得的测角误差较大,而载频参数相对稳定,就会造成来自该雷达的信号在数据空间呈现椭球体特征,在得到聚类中心和聚类数目后,若采取靠近原则对待聚类数据进行划分,则势必很难得到很好的分类结果。因此,根据待分类雷达信号的数据空间呈现椭球体的特征,本文提出采用GMM聚类算法来完成最后的数据划分任务,具体的实现步骤如下:

对待分类雷达信号数据进行归一化处理;

计算所有数据对象两两之间的欧氏距离;

利用斐波那契法对数据场中辐射因子参数进行最优化选择;

根据辐射因子计算各数据对象的势能和最近大势能点,根据势能对孤立噪声点进行剔除;

计算各数据对象的势能距离积,并进行降序排列;

计算各数据对象的势能距离积下降率,选择下降率最大的点为聚类中心与其他数据点的分界,得到聚类中心和聚类数目;

采用GMM聚类算法对剩余雷达信号进行划分聚类。

4 仿真实验与分析

为了验证本文算法在雷达信号聚类分选中的有效性,模拟13部雷达共2 549个脉冲信号。为逼近真实情形,在脉冲方位到达角(direction of arrival, DOA)和载频(radio frequency, RF)中加入测量误差,一般情况下脉冲宽度(pulse width, PW)越小、信噪比越低,引起的DOA、RF测量误差越大,且这种测量误差一般服从高斯分布。因此,在信号模拟中,对DOA、RF参数中加入的零均值高斯噪声,方差与PW大致呈反比关系。为消除不同维度数值量级对聚类算法的影响,每次仿真实验均对待分类数据进行0～1标准化处理。待分选脉冲数据在参数空间中的三维展示如图7所示,模拟雷达信号具体参数如表1所示。

图7 13部雷达脉冲信号在参数空间分布情况Fig.7 Distribution of pulse signals of 13 radars in parameter space

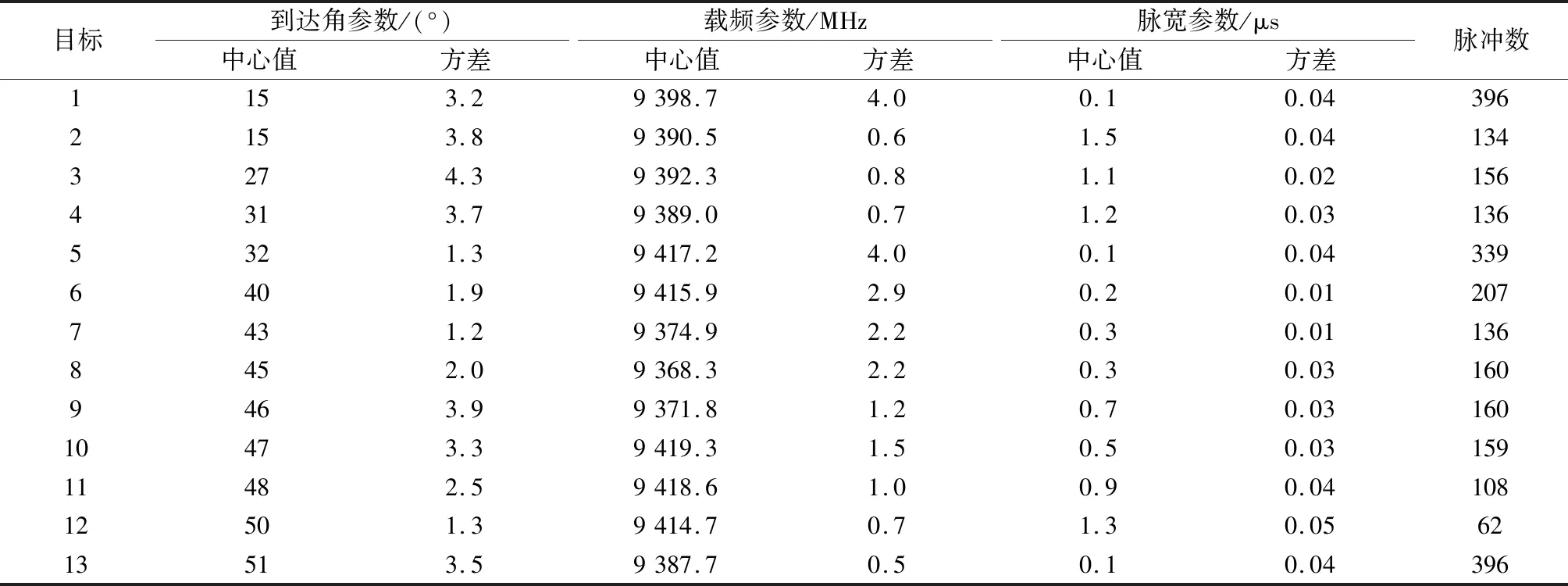
表1 模拟雷达信号参数信息Table 1 Parameter information of radar signal simulation

将本文方法同具备中心点自选择能力的改进K-means、改进数据场聚类、改进CFSFDP算法进行对比,分别从聚类准确度、算法鲁棒性和时间复杂度3个方面对本文算法性能进行验证。实验平台及参数设置如表2所示。

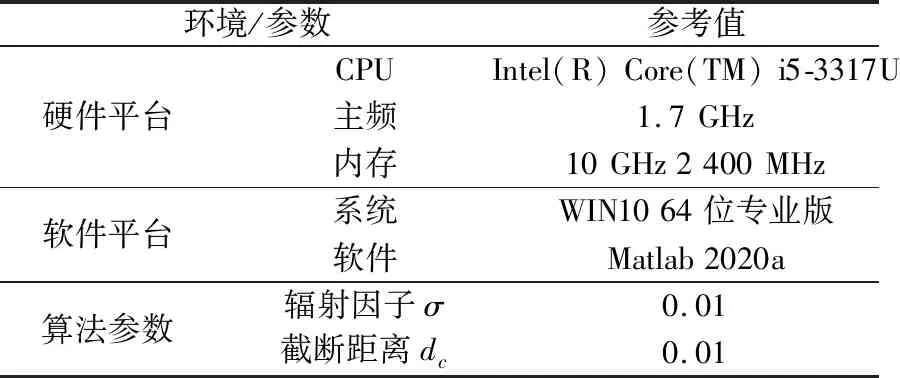
表2 实验平台及参数设置Table 2 Experimental platform and parameter setting

4.1 聚类准确度

4.1.1 聚类中心的选取准确度

为了对各算法在确定聚类数目和选择聚类中心方面进行对比分析,定义聚类中心选取误差为真实雷达目标中心点集合与算法选择的聚类中心点集合之间的Hausdorff距离。为了消除偶然性,每组实验进行100次,每次仿真均重新按照表1对待聚类脉冲数据进行重建和标准化,仿真结果如图8所示。

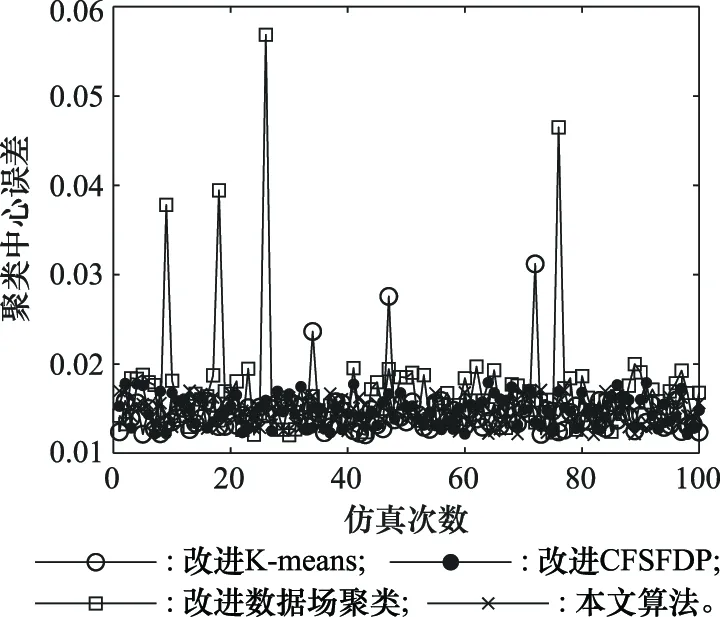
图8 聚类中心选取误差对比Fig.8 Comparison of cluster center selection errors

由图8可知,改进的K-means和改进数据场聚类算法出现几次误差较高的情况,考虑是聚类数目选择错误引起的较大误差。而改进CFSFDP总体呈现较小的聚类中心误差,本文方法采用自动中心点选择的策略得到的聚类中心误差与改进CFSFDP大致相当,本文提出的势能距离积下降率求边界点的方法用于聚类中心的选取是可行的。

4.1.2 整体聚类准确度方面

为评价各算法整体聚类准确度性能,采用聚类正确率评价指标对各算法分别进行仿真实验,各组实验分别进行100次评价指标取均值。仿真结果对比如表3所示。

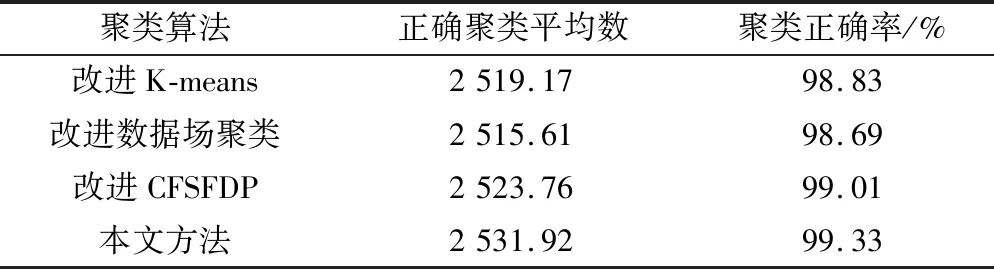
表3 算法运行时间比较Table 3 Comparison of algorithm run time

根据表3结果可知,本文方法在聚类正确率方面整体优于其他3种方法,而改进CFSFDP算法虽然在聚类中心选择方面具有性能优势,但在聚类准确度方面却低于改进数据场聚类算法,考虑是因为在确定聚类中心点以后,CFSFDP算法采用的是靠近原则对剩余脉冲数据进行划分聚类,而当两类雷达信号相距较近时,此类超球体的方式就容易发生错误划分。而本文方法在较高的聚类中心选择正确率基础上,采用GMM方法以椭球体的方式对剩余脉冲数据进行划分,从而取得了较高的聚类正确率。

4.2 算法鲁棒性

在实际外场环境中,由于噪声的起伏和检波门限设定等其他多方面原因,待聚类数据不会只有纯净的目标信号,往往存在孤立噪声干扰和目标脉冲丢失的情况。图9为加入20%孤立噪声脉冲干扰且经过标准化处理的待聚类数据,可以看出由于孤立噪声脉冲的存在,使得相对纯净的数据空间变得更为复杂,某些雷达信号之间由边界清晰变得相对难以界定,更加符合真实战场中的电磁环境。

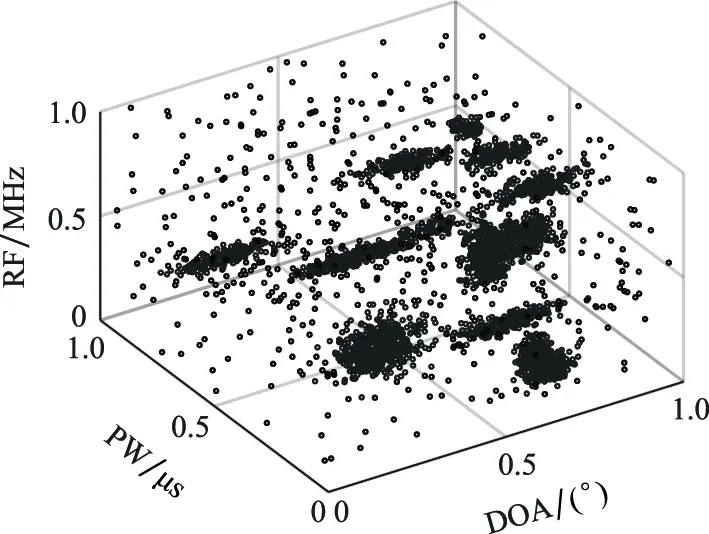
图9 加入20%孤立脉冲干扰的标准化后待分类数据Fig.9 Standardized data to be classified after adding 20% isolated pulse interference

为验证在模拟真实电磁环境下算法的鲁棒性,在表1所列目标信号基础上分别加入脉冲总数5%、10%、15%、20%的孤立噪声脉冲和脉冲丢失,将4种方法分别用于对上述混合信号进行分类处理,对比不同算法的聚类正确率。每组实验进行100次蒙特卡罗仿真,聚类正确率取均值,仿真结果如图10和图11所示。

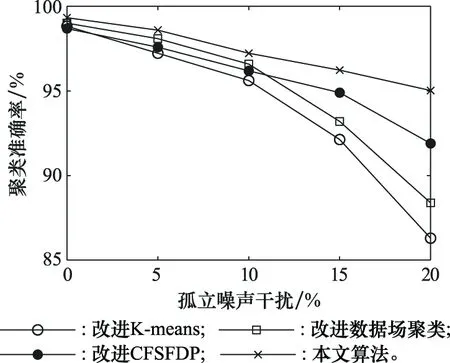
图10 存在孤立噪声干扰时聚类准确率对比Fig.10 Comparison of clustering accuracy in the presence of isolated noise

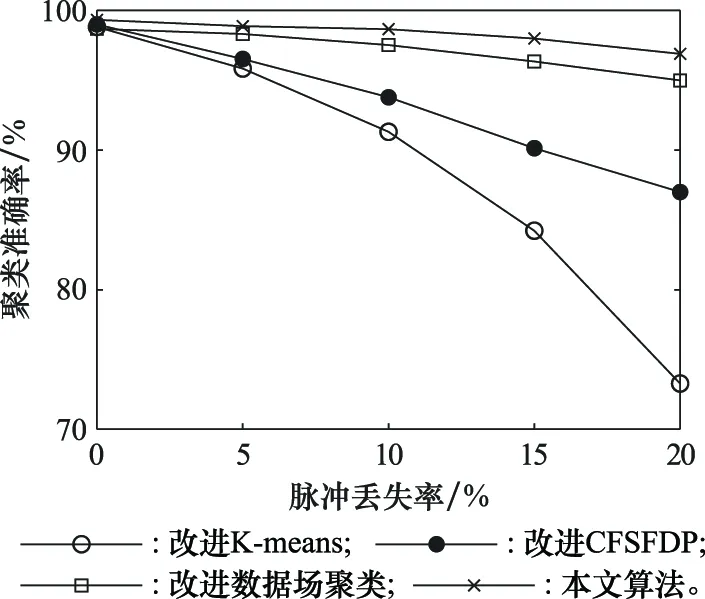
图11 存在脉冲丢失时聚类准确率对比Fig.11 Comparison of clustering accuracy in the presence of pulse loss

对比分析图10,在存在孤立噪声脉冲干扰的情况下,各算法聚类准确度均不同程度受到影响。其中文献[8]中的改进K-means算法需要先根据PRI变换法进行基于PRI的预分选,孤立噪声脉冲的存在会使PRI值估计误差变大,脉冲序列抽取过程中的干扰脉冲增多,准确率降低,导致后续基于K-means的聚类准确率随着孤立噪声脉冲的增加而出现严重下降。改进数据场聚类和改进CFSFDP聚类由于噪声脉冲的存在,一方面会不可避免地将部分噪声脉冲归入类中,另一方面将原本相近的两个雷达信号误判为一个联通的聚类簇,从而出现聚类中心选择错误的情况,导致聚类准确度随着孤立噪声脉冲的增加而出现不同程度的下降。而本文方法在加入孤立噪声脉冲后,虽然在确定聚类中心后的数据划分阶段受到一定的噪声干扰影响,聚类准确度随孤立噪声脉冲数量增加而有所下降,但由于首先根据数据分布选取最优辐射因子后对噪声脉冲进行了剔除,降低了孤立噪声脉冲在聚类中心选取阶段的影响,聚类中心选择相对准确稳定,且最后数据划分阶段采用了更适合处理非球体类聚类簇的GMM聚类。因此,在4种聚类方法中始终保持最高的聚类准确度,即使在存在20%孤立噪声脉冲的情况下,依然能够保持95%以上的聚类准确度。

根据图11可知改进K-means和改进CFSFDP算法随着脉冲丢失数量的增加聚类准确度存在一定下降,特别是改进K-means算法对脉冲丢失尤其敏感。主要是改进K-means算法中基于PRI的预分选阶段由于脉冲丢失的存在,导致脉冲串出现部分中断,影响了基于PRI的脉冲串标记,进而降低了整体的聚类准确度。由于改进CFSFDP算法采用固定的截断距离设定,而脉冲丢失改变了原数据密度分布,一定程度上影响了改进CFSFDP算法的聚类中心选择,导致聚类准确度有所降低。尽管数据场聚类算法对脉冲丢失不敏感,随着脉冲丢失的增多聚类准确度并未出现明显下降,但本文方法由于采用了最优辐射因子的数据场和聚类中心显著性自确定方法,以及在数据划分方面的改进,更加适合处理类似测量误差和有意调制导致的参数抖动信号的分类,使得本文方法聚类准确度略高于改进数据场聚类算法。

4.3 时间复杂度

电子侦察中的雷达信号处理分为实时处理和事后处理,其中实时处理作为战术侦察和电子支援系统的关键环节对算法处理速度提出了很高的要求,在目标信号较多的情况下处理不及时就会出现数据溢出的情况,可能会导致丢失重要目标数据。因此,为考察计算复杂度,对比不同算法、不同数据维数时的相对计算时间,根据表1中所列目标参数,生成共2 549个待分类脉冲数据,选取到达角和脉宽两个属性参数构成一组二维待分类数据,对二维和原DOA、PW、RF三维待分类数据分别进行聚类仿真实验,各组实验进行100次蒙特卡罗仿真,计算耗时取平均值,实验结果如图12所示。

图12 各算法计算耗时对比Fig.12 Comparison of calculation time of each algorithm

本文算法的时间复杂度主要由以下几部分组成:一是利用斐波那契法根据势熵迭代优化辐射因子,时间复杂度近似为();二是计算各点最近大势能点距离,并依势能距离积进行降序重排,时间复杂度近似为();三是确定聚类中心后对剩余数据进行基于GMM的聚类,该部分满足线性时间复杂度()。因此,本文算法的时间复杂度为(++)≈(),与上述改进K-means、改进数据场聚类和改进CFSFDP聚类算法()的时间复杂度基本相当,从图12中算法耗时的横向对比也得到了印证。可以说本文算法在提高了聚类准确率和鲁棒性的同时,并未显著提高算法的时间复杂度。但由于本文在最后数据划分阶段采用GMM聚类,需要在各维度上寻优,导致在数据维度增加后算法的计算时间上升幅度明显大于改进CFSFDP算法,后续需要针对数据维数增加对本文算法进行降低复杂度的针对性优化。值得说明的是,本实验所得各算法时间消耗受仿真平台和仿真软件限制,并不能如实反映算法在实际应用中的表现,仅限于同等条件下不同算法之间的性能比较。

5 结 论

本文针对雷达辐射源信号分选应用需求,提出了一种基于数据场联合决策图改进的GMM聚类算法。针对GMM算法需要输入初始聚类中心和聚类数目以及不断迭代带来的运算消耗大的缺点,提出将对噪声和脉冲丢失不敏感的数据场聚类和能够快速提出聚类中心的CFSFDP算法进行联合,优化了数据场中辐射因子参数设定和决策图中聚类中心点自选择方法。本文方法无需人工设定参数和人工辅助参与,能够根据待分类数据分布情况自动完成聚类。仿真实验分别从准确度、鲁棒性、计算量3个方面对算法进行了对比分析,实验结果表明,本文方法相较于改进K-means、改进数据场聚类和改进CFSFDP算法具有较高的准确度和鲁棒性,相较于改进CFSFDP提高了算法适应性的同时并未增加过多计算复杂度。对于存在一定测量误差和孤立噪声干扰的工程应用,本文算法对于提高分选能力具有一定的参考价值。

但限于GMM聚类算法仅适用于处理类椭球形数据,对于雷达辐射源信号可能存在的频率和脉宽捷变、分集等调制样式,本文算法聚类效果不够理想,可能存在将同一雷达的信号判定为多个不同的聚类。因此,下一步可以通过增加判别融合环节,将聚类后的可能来自同一雷达的不同类信号进行合并,以提高本文算法适应能力。