面向规则网格的连续天际线可视域精确算法

张建民，余接情，艾 伟，杜 丹

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.河北省智能化信息感知与处理重点实验室，河北 石家庄 050081;3.中国矿业大学环境与测绘学院，江苏 徐州 221116;4.陆装驻石家庄地区第一军代室，河北 石家庄 050081)

0 引言

设施选址[1]、景观分析与规划[2-3]、军事突防[4-5]、安防监控[6]及信号盲区计算[7-8]等问题均需获取相对视点可见的表面区域，即可视域计算。计算机中，地形表面常采用基于规则网格的数字高程模型来描述。为此，可视域计算通常为寻找相对于视点的所有可见网格。某一网格可见当且仅当其与视点连线不被其它网格遮挡。

作为地理信息系统空间分析的经典问题，可视域计算已有较多研究。Shapira[9]提出了一种精确的可视域计算算法―R3算法。该算法为每一网格引一条视线，通过视线是否被阻挡来判断每一网格的可见性。由于每一网格的可见性除当前网格外还涉及视线所途经的网格，为此，R3算法的计算量极为庞大，时间复杂度达O(n3)，其中，n为地形沿某一维度的网格数量。为提高算法速度，Kreveld[10]提出了一种时间复杂度为O (n2logn)的扫描线(Sweep Line,SL)算法；Franklin和Ray[11]提出了一种时间复杂度为O(n2)的xDraw算法和R2算法；Wang等[12]基于视线后方邻近网格的视面提出了一种更快的参考面算法。事实上，当前网格是否可见不仅与视线后方邻近网格有关，还与离视点更近网格所构成的视面有关。对此，Yu等[13]提出了一种视面综合算法(Synthetic Visual Plane, SVP)，将任意相邻网格构成的视面投影至远处的投影面，形成一条天际线，通过合成多条更近天际线以获得当前天际线，从而判断当前网格的可见性。为提高算法效率，该算法以一定的精度损失为代价对天际线进行了离散化处理。

然而，精度是可视域计算的重要考虑因素。Kauci和Zalik[14]将可视域计算算法分为精确算法和近似算法。除R3算法和SL算法外，上述均为近似算法[13-16]。实际应用中，可视域计算既要考虑时间性能也要考虑算法精度。例如，飞机突防应用中，错误的可视域结果会为突防飞机带来风险，而较低的计算效率又难以满足应用要求。对精确算法进行并行化改造是一种可满足上述要求的方案。Zhao等人[15]及Chaulio等人[16]利用并行计算分别对R3算法和SL算法进行了改造。然而，并行化方案虽可行但终究依赖硬件，特定场合下难以适用。

本文在SVP算法的基础上改进描述方法并设计了高效的数据结构与算法来应对天际线描述方式变更后所带来的天际线快速更新问题，提出一种高效且精准的可视域计算算法。

1 SVP算法介绍

图1为SVP算法[13]示意图。该算法以视点为中心将规则网格表示的地形划分为4个扇区和若干个环，并为每一扇区在离视点一定距离处设立一个投影面，如图1(a)所示。算法将前序所有环的每一网格点投影至投影面以得出前序天际线。天际线被定义为将某一环上各网格点投影至投影面并依次连接所形成的一条连续线段。若当前环的某一网格点的投影(以下简称投影点)在前序天际线上面，则当前点可见，否则不可见。该算法的关键在于获取当前环的各投影点后如何更新前序天际线。为提升效率，SVP算法对天际线进行了离散化，如图1(b)所示。将投影面以一定间距划分为若干条带，借助条带对天际线进行离散化采样。更新时，若某一条带的当前投影高程高于先前投影高程，则更新该条带的投影高程。由于离散化后的天际线更新特别快，为此，SVP算法效率很高。

SVP算法时间效率与参考面算法相似但精度更高，比R2算法时间效率更高，但精度略差。虽然可通过缩短条带的间距以提高SVP算法的精度，但这样会成倍增加算法的时间消耗，甚至可能超过R3算法，使得该操作无过多实际应用价值。

图1 SVP算法示意图

2 连续天际线可视域算法

为方便起见，将本文提出的新算法称为连续天际线可视域(Viewshed based on Continuous Horizon, VCH)算法。VCH算法以SVP算法为基础，通过改进其天际线的表达与更新方法来实现可视域的精确计算。

2.1 算法原理与流程

如上所述，SVP算法的核心之一是对天际线进行离散化。虽然离散化可提高算法的速度，但也带来了误差，降低了算法的精度。为避免该问题，VCH算法采用连续线段来表达天际线。与此同时，为避免连续线段天际线更新的效率低下问题，引入了红黑树[17]来动态管理该天际线。

VCH算法以视点为中心，以两条45°对角线为界将规则格网表示的地形表面划分为4个扇区，再根据同心方环的顺序依次由内向外划分为若干个环，如图1(a)所示。为避免扇形边界重复投影问题，VCH算法在四个方向上同时设立了一个投影面，形成了一个闭合的投影墙, 如图2所示。VCH算法的总体流程如下：

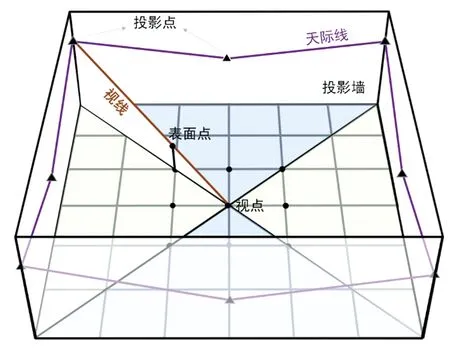
图2 投影墙及初始天际线示意图

(1)将第一环上的表面点投影至投影墙(第一环上的表面点总为可见)，形成一条初始天际线，设置第二环为当前环；

(2)投影当前环的表面点至投影墙上，然后由前序天际线来逐一判断当前环各表面点的可见性；若表面点投影位于前序天际线之上，则可见，否则，不可见；

(3)根据当前环各投影点高程更新前序天际线；

(4)视更新后的天际线为当前环及前序环所对应的天际线(即下次循环的前序天际线)，用于后续环表面点的可见性判断，重复步骤(2)至步骤(4)，直至所有环均被处理为止。

一条天际线由若干条片段构成，上述流程的关键在于根据当前环各投影点所形成的片段来更新前序天际线。为加速该更新过程，本文采用了红黑树及双向链表这一数据结构来共同存储与管理一条天际线，如图3所示。双向链表的每个节点由头尾两个指针和数据体构成。数据体记录投影点的y和z坐标。双向链表的每个节点按照其y坐标的升序进行排列。红黑树的每个节点记录投影点的y坐标及其在双向链表对应节点的地址。

图3 天际线数据结构图

更新时，需根据当前片段的前后两个端点的y坐标值，从红黑树中依次寻找出对应的节点，进而根据找到的地址从双向链表中获取相应的前序片段集。前序片段集为前序天际线中的多个连续片段的集合。集合中的首片段的起点y坐标不小于用于检索片段的起点的y坐标，而集合中的末片段的终点y坐标不大于用于检索片段的终点的y坐标。图4为天际线更新示意图，其中，线段集I-II-III为片段BC所对应的前序片段集。获取前序片段集后，按下述规则将当前片段合成并更新至前序天际线(或前序片段集)中。

图4 天际线更新示意图

(1)若当前片段的某个投影点(图4中的A)y坐标与前序片段集的某一顶点(图4中的I)的y坐标相同，且投影点的z值更大，则用该投影点的z值替换前序片段集对应顶点的z值；

(2)若当前片段的某个投影点(图4中的C和D)位于前序片段集的顶部，且其y坐标不与前序片段集各顶点的y坐标相同，则将该投影点作为一个新的顶点插入至前序天际线中；

(3)若当前片段(图4中的AB、BC及DE)与前序片段集存在交点(图4中的S1、S2和S3)，且交点的y坐标不与前序片段集各顶点的y坐标相同，则将交点作为一个新的顶点插入至前序天际线中；

(4)若前序片段集的某一顶点(图4中的Ⅲ)位于当前片段(图4中的CD)的正下方，且该顶底的y坐标不与当前片段的两个端点y坐标相同，则将该顶点从前序天际线中删除。

2.2 时间复杂度分析

为分析VCH算法的时间复杂度，下述伪代码给出了其总体实现。

Algorithm:VCH 输入:(1)规则网格地形表面点 (2)视点、视高及最大视野范围(r)输出: 可视域图1.投影第一环地表点得初始天际线。2.For i in [2,r] 3. For j in [0, m]//m为当前环的地表点总数4. 若Pji位于前序天际线上方,输出可见;否则,输出不可见。//Pji为第i环的第j个点5. 寻找当前片段(Pj-1i, Pji)的前序片段集。6. 更新当前片段至前序片段集(或前序天际线)中7. End For8.End For

易知，语句1和语句4的复杂度为O(1)。语句5涉及从红黑树中寻找特定的节点，对应的时间复杂度为O(logm)[17]，其中，m为前序天际线的顶点数量。假定前序天际线是由前k个环所合成的天际线，则m必然小于8×(1+2+…+k)，这是因为不同环的表面点投影后的y坐标可能相同。显然，k越小，m越小，反之亦然。若将m平摊至每次循环中，则一条前序天际线平均拥有不多于4+4n个顶点，其中，n为最大视野范围所对应的沿某一维度的网格数量。为此，语句5的时间复杂度为O(logn)。语句6涉及红黑树及双向链表的节点插入与删除。红黑树的插入和删除操作的时间复杂度均为O(logm)[17]。在已知待插入或删除节点位置的情况下，双向链表的插入与删除操作的时间复杂度为O(1)。同理，语句6的时间复杂度为O(logn)。

综上分析，易知VCH算法的总体时间复杂度为O(n2logn), 其中，n表示最大视野范围所对应的沿某一维度的网格数量。

3 实验与比较

3.1 精度验证

VCH算法根据前序天际线来判断某一表面点是否可见，而前序天际线反映了所有更近点的遮挡情况。为此，理论上VCH算法是一种精确算法。由于可视域的真值难以获取，本文以公认的精确算法[13-16]-R3算法为参考进行精度验证。R3算法采用点的高程是否比其可视高程大的方式来计算，而VCH算法采用点的投影是否在其对应的前序天际线上面的方式来计算。临界点与可视高程如图5所示，由于浮点计算误差的存在，不同的计算方式会导致临界点(即该点的高程与可视高程极为接近，如图5的B和C所示)的可见性结果迥异。虽然理论上VCH算法是精确算法，但其结果可能不与R3算法的结果完全相同。

图5 临界点与可视高程示意图

为测试VCH算法的精度，使用了东经115.5°至117.5°、北纬28.7°至30.3°的ASTER DEM数据开展了实验。实验采用了世界墨卡托投影，设置视点为(12968717.010,3419826.095)、离地高度为100 m、最大视野范围为50 km，统计了VCH算法与R3算法不同结果的网格，包括假正(false positive)网格和真负(truth negative)网格。假正网格指R3算法可见但VCH算法判为不可见的网格；真负网格指R3算法不可见却被VCH算法判为可见的网格。表1给出了VCH算法结果中的所有网格、假正网格及真负网格的数量。可以发现：VCH算法的假正及真负网格的占比极为微小。

表1 VCH算法中各类网格数量统计表

图6 各假正及真负网格所对应的最小视高差图

为测试VCH算法中假正及真负网格是否为临界点网格，引入了视高差这一概念。从视点出发引一条视线至待测试的网格点，计算各途径点与该视线的距离，即视高差(图6)。若某一途径点的视高差接近于零，则表明待测试网格点是一临界点。VCH算法所有假正及真负网格的最小视高差的分布(按从大至小顺序排列)如图6所示。可以看出，最小视高差不超过10-12m，意味着VCH算法所有假正及真负网格所对应的表面点均可认为是临界点，即VCH算法的假正及真负网格由浮点计算误差产生。若不计浮点计算误差的影响，VCH算法与R3算法结果将等同。也就是说，VCH算法是一种精确算法。

3.2 性能比较

为测试与比较VCH算法的时间性能，利用C++实现了R3、SL(由开源软件GRASS提供)、VCH、R2及SVP算法，并在Intel i5-7500 CPU(单核主频3.40GHz、64位)、8GB DDR内存、东芝1TB 7200转机械硬盘的硬件环境下运行。实验除最大视野范围不同，数据及其它参数均与3.1节保持一致。此外，为便于横向比较，设置初始最大视野范围为10 km，之后以10 km为间隔依次增大直至80 km为止。图7为各算法的时间消耗。可以看出，R3算法的时间消耗最大、SL其次、剩下依次为VCH、R2及SVP，而后三者较为接近。所有算法的时间消耗随最大视野范围的增大而增加，但VCH的增幅明显小于R3及SL，略大于R2及SVP。

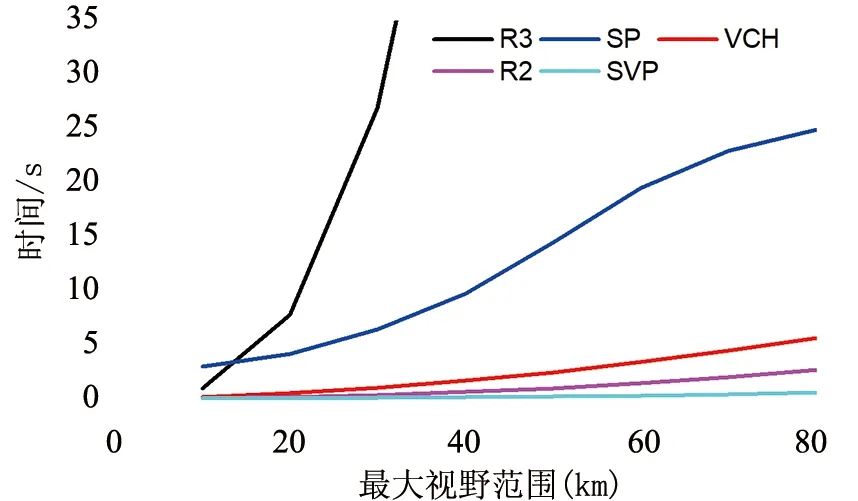
图7 各算法的时间消耗图

4 结束语

围绕现有可视域算法在精度及效率难以同时达到较高性能这一问题，本文以视面综合算法为基础，基于连续天际线思想及红黑树与双向链表提出了一种新的可视域算法。新算法可在保证结果完全准确的情况下将时间复杂度控制在O(n2logn),其中，n为最大视野范围沿某一维度的网格数量。与R3精确算法(时间复杂度：O(n3))相比，新算法的时间性能提升了一个档次。虽然与扫描线精确算法相比新算法的时间复杂度没有降低，但真实实验表明新算法比扫描线快得多，其时间性能可与现有的近似算法相媲美。

新算法可用于对精度和时间要求均很高的应用，如低空突防，信号盲区计算等。后续研究将对该算法中的天际线数据结构进行改进以进一步提升算法的效率。