中国碳达峰模型研究综述

王侃宏，何 好

(河北工程大学能源与环境工程学院，河北 邯郸 056038)

0 引言

随着经济快速发展，工业进程加快，人类的过度活动导致全球气候发生了显著变化，极端天气气候事件频发。联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change, IPCC)第六次评估指出，未来全球绝大部分有人口居住的地方都将出现更多、更强、更持久的极端高温[1]。减少温室气体(主要是二氧化碳)排放，减缓全球升温成为了国内外科研人员的研究热点。

气候变化已经接近不可挽回的临界点，全球气候变暖问题也成为了国际社会的关注焦点，为此世界各国签署了《巴黎协定》，确定到本世纪末全球控温低于2℃的目标，并争取将气温升幅限制在1.5℃。作为一个负责的发展中大国，习近平总书记在第75届联合国大会上提出了CO2排放力争于2030年前达峰，努力争取2060年前实现碳中和的“双碳”目标[2]。在“双碳”目标背景下，了解碳排放影响因素、达峰时间、峰值，对碳排放总量和强度的控制起到了决定性作用。

1 我国碳排放达峰研究简述

中国作为全球最大的碳排放国家和全球第二大经济体，2017年碳排放总量为9.30 GtCO2，约占全球总量的28.27%，且尚未实现碳达峰[3]。碳排放达峰预测研究对于各地区、各领域、各行业等制定碳达峰行动方案等具有重要意义。通过文献检索，多数学者对于碳达峰问题的研究主要集中在国家层面，省市层面和行业层面次之，对于园区、企业层面的研究相对较少。

1.1 碳排放峰值预测研究

首先，在国家层面，部分研究学者通过模型预测和情景假设进行分析，柴麒敏[4]等人基于自主构建的综合评估模型IAMC设置了四种路径和情景进行模拟，预测出中国将在“十五五”末实现120 亿t的碳排放峰值。Sun Z[5]等人利用IPAT模型设置情景分析，结果表明，中国将于2030年达峰，峰值为10.57Gt，河北、山东、内蒙古等地是完成减排任务的重点地区。王勇[6]等人构建包含气候保护函数的七部门CGE模型，模拟评估中国不同年份实现碳达峰对经济的影响，研究得出2030年是中国碳排放达峰的最佳时间点。张楠[7]基于全国30个省市区域划分建立CGE模型，研究表明，中国碳排放总量将在2025年实现峰值,此时碳排放总量应在100亿t以内。Fang K[8]、Su K[9]等人，通过构建STIRPAT模型结合情景分析预测得出我国碳排放峰值和达峰时间。

其次在省市层面，目前，研究者们多对单个省份或城市进行碳排放趋势分析、达峰时间和峰值预测，翁智雄[10]等人运用协整检验和马尔科夫链对河北省不同经济增长路径下的碳排放量进行了预测，预测得出在经济高速发展情景下，二氧化碳排放量将达到159117.415万t。朱宇恩[11]采用IPAT模型对山西省中长期能源碳排放量以及峰值年进行了预测，结果显示，在中低速发展情景下山西省的达峰时间为2030年，峰值为6.6亿t-7.1亿t间。刘茂辉[12]、闫新杰[13]、萨和雅[14]和张哲[15]等学者均采用STIRPAT模型并设置不同的情景分别预测了天津市、新疆、内蒙古自治区和上海市等省市的碳排放峰值和达峰时间。邱硕等[16]以陕西省为例，基于陕西统计年鉴建立LEAP模型，在基准情景下，CO2排放在2030年达到2.68 万t，节能减排综合情景下, CO2排放在2021年达到峰值2.48 万t，工业、交通及发电部门贡献水平最高。李彬[17]根据北京应对气候变化的多重目标，基于IPAC模型框架，开发了IPAC-Beijing模型，结合情景分析法，得出在强力低碳政策情景下，北京将在2025年达到峰值，能源消费总量为1.4亿t左右，碳排放达到2.4亿t的峰值。也有不少学者如马宇恒[18]、潘栋[19]等同时对多个省份或城市的碳排放趋势进行比较分析。

从行业层面角度看，碳排放的主要来源为电力、建筑、工业和交通运输领域，行业的达峰时间、峰值大小，直接或间接地影响了城市和国家层面的碳达峰实现。张金良[20]等人基于扩展的Kaya恒等式，建立了包括BP神经网络模型的多种预测模型，在最优预测模型基础下设置多种发展情景，对火电行业2021—2050年的碳排放量进行预测。刘菁[21]利用拓展型STIRPAT给出的影响因素分析,结合系统动力学方法，对建筑全产业链的碳排放量进行了趋势预测。张为程[22]将情景分析法与LEAP模型相结合，研究了四种发展情景下吉林省民用建筑运营期间的碳排放，研究表明不同情景下，民用建筑碳达峰时间为2026—2040年,峰值介于47.50Mt-58.17Mt间。代大为和张凌[23]基于扩展的Kaya公式结合LMDI模型分析了安徽省工业碳达峰影响因素，运用灰色预测模型(EGM1,1)预测了2020—2029年的碳排放量变化趋势。朱长征[24]等人利用岭回归构建了碳排放预测模型结合情景分析法，对中国交通运输业碳达峰情况进行预测分析，结果表明，强化低碳情景是中国交通运输业碳排放达峰的最佳发展模式，达峰时间为2030年，峰值10.31亿t。宋嗣[25]基于可计算一般均衡模型原理,构建IPAC-SGM模型，应用此模型分析了我国国民经济和交通能耗之间的相互作用，在三种碳税情境下，在2032年之前经济发展对我国交通行业的能源消耗降低和运输结构转变均呈负面影响。

除国家、省市和行业层面，对于类似园区、企业等小区域层面的碳达峰预测研究成果相对较少，周德群[26]等人通过建立多情景仿真模型对园区碳减排潜力和“双碳”路径进行分析，研究得出在一系列措施情景下，园区有望在2030年达峰，2055年中和。杨培志和韩春洋[27]基于LEAP模型对长沙市某产业园区未来能源需求及碳排放进行预测，并提出相应的碳减排政策。

1.2 文献研究总结

综上所述，从研究范围来看，现阶段我国碳达峰相关研究仍以国家、省市层面为主，从宏观的角度，将国家、各省市作为一个整体进行碳排放影响因素、碳达峰峰值及达峰路径的研究。研究范围从国家、省市到行业再到园区、企业依次递进，为区域未来能源规划和减排政策提供参考。从研究方法看，各学者所使用的模型方法有所不同，主要包括STIRPAT模型、LMDI模型、Kaya恒等式、LEAP模型、CGE模型等，基于各区域的历史数据和发展规划，分析得出政策、经济发展水平、能源产业结构调整等多方面影响因素与碳排放之间的数学关系，进行不同发展情景的设定，预测未来CO2排放达峰时间和峰值，具体见表1。下文对具有代表性的模型做简要介绍说明。

表1 中国碳排放达峰研究汇总表

2 碳排放影响因素研究方法

2.1 STIRPAT模型

人口、富裕和技术的随机回归影响模型STIRPAT(Stochastic Impacts by Regression on Population, Affluence, and Technology)是一种随机模型，由IPAT等式发展而来。IPAT等式于20世纪70年代初首次提出，Ehrlich和Holden[28]为研究人口、人类福利和环境压力之间的作用关系，把环境压力(I)归结为人口(P)、富裕(A)和技术(T)3个关键驱动因素乘积的结果，其表达式如下:

I=P×A×T

(1)

然而，IPAT等式存在一定的局限性，其默认环境压力(I)与各驱动因素之间成1∶1的等比例对应关系，即不同因素对环境压力的贡献相同。在此基础上，许多学者对其进行改进，其中，Dietz T[29]等人提出了STIRPAT模型，以此弥补IPAT等式的缺陷，STIRPAT模型表达式如下:

I=aPbAcTde

(2)

其中，a,b,c,d分别为模型系数及各影响因素P,A,T项的指数，e是误差项。指数越大，表明受到此因素的影响越大，误差项e则表示模型中未考虑到的其他因素影响大小。当a=b=c=d=1时，STIRPAT模型就还原成IPAT等式。为便于估计和假设检验，消除模型中可能存在的异方差影响，通常情况下，将其转化为对数形式：

lnI=a+blnP+clnA+dlnT+e

(3)

在实际应用过程中，部分研究学者[18-19]会根据需要在公式中增加其他影响因素如城市化率、能源结构、产业结构等来分析多种因素对环境的影响程度，并结合情景分析法对STIRPAT模型进行补充，得出更加可靠的排放轨迹和碳排放峰值路径预测结果。目前，STIRPAT分析模型已被公认为识别与能源相关的碳排放背后的社会、经济和技术驱动因素的有效方法[30]，在国内应用非常广泛。

2.2 Kaya恒等式

Kaya恒等式是日本学者Yoichi Kaya[31]于1989年在IPCC第一次讨论会上提出，Kaya恒等式在IPAT模型的基础上进行了扩展，用简单的数学公式将碳排放量与经济、政策和人口等因素联系起来，直观地展示了碳排放的驱动因素及其影响程度。Kaya模型表达式如下：

(4)

其中，CO2表示CO2排放量；E为一次能源消费量；GDP为国内生产总值；P为国内人口数量；CO2/E为单位能耗的碳排放量；E/GDP为单位GDP能耗，即能源使用强度；GDP/P为人均GDP，即富裕程度。对式(4)进行微积分变换得到式(5)，在计算各驱动因素的影响程度时，多采用微分形式。

(5)

Kaya恒等式具有形式简单、分解无残差、对碳排放变化驱动因素解释力强等优点，被广泛应用于不同国家地区，是当前进行碳排放影响因素分析的主流方法之一，但其也存在一定的局限性：只能解释碳排放量流量变化而无法解释存量变化；等式中的驱动因素主要为表象驱动因素, 难以确定碳排放总量的实际影响，利用Kaya恒等式理论得到的政策建议具有模糊性和非理性，需要与其他因素结合进行分析检验[32]。因此，为克服Kaya恒等式的局限性，研究者需结合实际情况进行扩展，如Kavgic M[33]等人为更直接地研究建筑部门碳排放及其减碳路径，对Kaya恒等式进行简单变形，得到适用于建筑部门碳排放研究的Kaya模型。

2.3 对数平均迪氏因素分解法(LMDI)

指数分解分析法分为拉式(Laspeyres)指数法和迪氏(Divisia)指数法两大类，1997年Ang[34]等人提出的对数平均迪氏因素分解法LMDI(Log-Mean Divisia Index)是迪氏指数法的改进。LMDI指数分解法[35]具有易于分解、无残值和数据零值、容易使用且分解结果唯一等特点，是能源消费和碳排放研究中广泛使用的方法之一。LMDI指数分解法分为两种：加法分解模型和乘法分解模型。加法分解模型是将碳排放量在一个时期内绝对值的变化进行分解，分解出各影响因素变化导致的碳排放增量；乘法分解模型是将基准期和报告期的碳排放值表示为各因素相对贡献的乘积[36]。两种分解模型的最终结果相同，但加法形式由于能够更加清晰地分解出影响因素而被多数学者使用。

LMDI因素分解法的加法模型和乘法模型形式见式(6)、式(7)[37]。

(6)

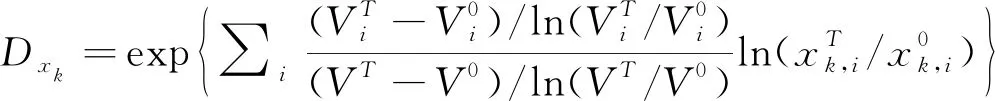
(7)

其中，V为目标量，x为不同的驱动因素。不同的研究根据实际情况将目标变量分解为若干驱动因素的组合，根据各个因素的数据来判断其影响程度。

3 达峰预测研究方法

碳达峰预测的模拟方法主要为“自上而下”模拟法、“自下而上”模拟法和综合评估模型三大类。“自上而下”模拟法是在宏观经济和社会发展规划的基础上进行模拟，反映了政策冲击在各个部门间的传导效应，模拟在政策冲击下各部门及各经济主体的反应，但该模拟方法无法确定具体的达峰路径；“自下而上”模拟法基于具体的技术信息，如减排措施和成本等，来确定合理的达峰目标和路径，但该方法对各技术的参数要求较高；综合评估模型是“自上而下”和“自下而上”两种方法的结合，通过对经济和技术各方面因素考虑，进行能源消费和碳排放测算，为各部门制定“双碳”政策提供支持，因此该综合评估模型结构较为复杂[38]。下文对以上三类方法的典型模型做简要介绍说明。

3.1 可计算的一般均衡模型(CGE)

可计算的一般均衡模型(CGE)由Walras提出，1894年Walras第一次从数学角度完整而充分的论述了一般均衡概念[39]。CGE以现代微观经济学为理论基础，利用非线性函数描述了供给、需求和市场间的关系，在一系列优化条件下，如生产者利润、消费者效益、进口收益和出口成本等，模拟各个市场的均衡状态[40]。部分学者针对碳排放相关研究，通过在CGE模型中加入碳减排措施等相关模块来定量评估该措施对宏观经济所造成的影响，如碳税、碳交易、碳捕集与封存和能效提升等。GCE模型具有以下特点：(1)能够准确地描述经济部门与其他各部门(如能源部门)之间的相互影响；(2)引入价格激励机制，将各因素有机结合，如生产、需求，价格等，模拟了混合经济下，各部门应对政策冲击的价格变动反应；(3)以微观经济学为理论基础，相较于宏观经济模型，其分析基础更坚实，适用性强[18]。基于上述特点，CGE模型在气候变化政策相关研究中被广泛应用，在气候变化政策领域，研究者们根据研究领域的具体情况，建立了自己的CGE模型，毛亚林[41]运用针对中国经济发展特征设计的一个递归动态可计算一般均衡(CGE)模型-CHINAGEM模型，对当前政策情景和碳中和情景进行模拟分析,预测分析2020—2040年中国能源发展状况。当前，CGE模型主要存在的问题有：结果依赖大量参数且参数取值不稳健，模型假设过于理想且技术表达抽象。因此，各研究者需充分借鉴先进模型开发的经验，重点研究我国在非理想与不均衡市场环境下经济行为表述的改进，更加注重基础数据的整理与重要参数的校核[42]。

3.2 长期能源替代规划系统模型(LEAP)

长期能源替代规划系统模型LEAP(Long Range Energy Alternatives Planning System)是由瑞典斯德哥尔摩环境研究所SEI开发的一种“自下而上”的能源-环境核算工具，主要用于国家、省市、行业的中长期能源规划。LEAP模型基于情景分析法，利用插值、外推和增长率等函数来模拟不同情景下各部门的能源需求、环境影响和成本效益。LEAP模型数据结构灵活、支持多种建模方法、具有强大的可视化功能和数据库，可以将研究范围内的关键部门分为多个子部门对此进行详细分析，并可与一般的经济模型等其他模型结合使用；模型主要包括五大模块，分别为能源需求、能源转化、生物质资源、环境影响评价和成本分析，通过对历史数据分析，假设未来的能源发展趋势，对政策措施、经济状况、技术水平、社会成本等因素进行设定，建立数据模型，得出相应的预测结果，因而对基础数据收集的要求也较高。该模型的缺点是没有优化功能，只能用于情景核算，且受基础数据的限制，难以进行完整的定量分析[18]，LEAP模型框架如图1所示。

图1 LEAP模型结构图[43]

3.3 中国能源政策综合评价模型(IPAC)

中国能源政策综合评价模型(IPAC)是国家发改委能源研究所与国内外的研究机构合作开发的结合中国发展特征的能源政策评估模型系统。IPAC模型主要包括能源与排放模型、环境模型和影响模型3个部分[44]。能源与排放模型包括能源经济模型(IPAC-SGM)、经济能源发展模型(IPAC-CGE)、动态能源经济模型(IPAC-TIMER)、能源与排放情景模型(IPAC-Emission)等；环境模型主要包括大气扩散模型(IPAC-Air)和简单气候模型(IPAC-Climate)；影响模型主要涉及的是健康影响评价模型(IPAC-health)。各子模型间相互关联，一个子模型的结果将会作为另一个子模型的输入，第一步先将能源与排放模型的结果输入到环境模型中，计算相关能源活动可能造成的环境变化；第二步将环境模型的输出结果输入到影响模型中，计算其对健康产生的影响，最后将这种影响转换为对经济发展的影响后再反馈回能源排放模型[45]。IPAC模型的框架如图2所示。

图2 IPAC模型结构图[46]

IPAC模型分析层面覆盖生产、居民、政府、贸易等相关领域，根据不同研究领域建立不同目标函数并结合情景分析，对各领域不同情景下的能源需求、社会成本收益和环境影响进行评估；同时，IPAC模型作为针对理论进行研究与分析的模型，因其涉及的数据较多、计算较为繁杂、耗时长，存在着一定的局限性，其应用较少[25]。

4 结论

国内不同学者在碳达峰研究课题上尝试了多种方法，可以看到，不同模型方法的数据库、理论基础、支撑假设等不相同，所预测的结果也不尽相同，这是由于碳达峰预测涉及多方面因素，包括政策、经济、技术等，达峰预测是一项极其复杂的研究工作，也因此导致了研究结果的不确定性。不同的模型方法在进行未来能源消耗和碳排放量预测中各有利弊，哪一种模型方法最合适主要取决于具体的研究重点，研究者有必要结合实际研究不断调整和更新建模方法、技术，明确模型主要驱动因素，对所用模型进行深入的分析或拓展，以确保预测结果的可靠性，得出合理的达峰路径。