致密油藏水驱井间裂缝网络参数反演方法及应用*

第五鹏祥 张 潇 李彦阅 李阿巧 赵旭东 李俊键

(1.中国石油大学(北京)理学院 北京 102249； 2.中海石油(中国)有限公司天津分公司 天津 300452；3.中国石油大学(北京)石油工程学院 北京 102249)

致密油藏中普遍存在不同发育程度的裂缝，水力压裂和高压注水使裂缝互相沟通，容易在注采井间形成裂缝网络[1]。注入水在井间裂缝网络内低效-无效循环，导致采油井见水时间提前、含水上升速度加快，出现严重的水窜现象，限制致密油藏注水开发效果[2]。准确地量化导致注入水窜流的井间裂缝网络，既是提高水驱开发效果的重要工作，也为后续介入提高采收率技术提供油藏地质认识基础[3]。

裂缝静态反演技术利用地震、测井等资料，可以得到储层裂缝发育情况，能够回答储层中裂缝多少的问题。目前致密油藏裂缝静态反演可总结为基于井点裂缝参数的插值法、基于地震数据的裂缝分布预测方法和多参数智能判断方法。直接插值法利用井点处岩心观察、薄片分析、测井等得到的裂缝数据，结合地震资料约束，通过插值预测储层裂缝的井间分布[4-6]。基于地震数据的裂缝分布预测方法通过计算地层曲率、岩石破裂值、古构造应力场等，对储层裂缝分布进行预测[7]，主要包括曲率法[8]、能量法与岩石破裂法(二元法)[9]、地震法[10-11]、构造应力场数值模拟法[12]等。多参数智能判断方法综合井点裂缝参数、岩石材料参数和应力场资料，以解决裂缝发育影响因素众多带来的反演问题[13-16]。上述方法的基本思想是根据静态资料反映的裂缝参数，反演储层裂缝分布，得到的是油藏投产初始状态的裂缝分布特征。

对于致密油藏水窜问题，不但需要量化井间裂缝网络规模，即注采井间裂缝多少的问题；而且需要明确井间裂缝网络表现出的渗流能力，即注采井间裂缝开度和连通关系的问题。由于致密油藏一般注水压力高，水驱过程中裂缝常会膨胀、延伸[17]和转向[18]，形成诱导裂缝[1]。赵向原 等明确了注水诱导裂缝(Waterflood Induced Fracture)的概念，这种裂缝是在长期注水开发过程中，当注水压力超过裂缝开启压力或地层破裂压力而形成的[1]。诱导裂缝使得储层裂缝分布异于初始状态[19]，裂缝连通关系得到改善[20]。同时，采油井和注入井近井地带地应力场会重新分布，导致裂缝闭合或裂缝转向的情况[21]。注水开发过程中井点裂缝参数和地应力场都会发生变化，井间诱导裂缝生成于重分布的地应力场，扩展方向和裂缝参数异于天然裂缝。因此，需要建立一种致密油藏井间裂缝网络动态反演方法，解决水驱过程中裂缝分布和连通关系发生变化后带来的量化难题，实现井间裂缝网络规模和渗流能力特征参数的量化。

综上，针对致密油藏水驱开发中井间裂缝网络量化的需求，设计以低效-无效循环注入水反演井间裂缝动态特征参数的思路。首先综合考虑裂缝开度的随机性质和形态的二叉树特征，建立了致密油藏水驱中井间裂缝网络物理模型；然后构建了注入水运移数学模型并解析求解；最后开展了井间裂缝网络参数反演的实例应用，讨论了致密油藏水驱过程井间裂缝分布特征。本文实现了基于动态数据的井间等效裂缝形态、数量和开度量化，为提高致密油藏水驱开发效果提供了数据基础。

1 井间裂缝网络的物理模型

1.1 井间裂缝的形态特征

水力压裂在近井地带形成天然裂缝和压裂裂缝沟通的裂缝网络，高压注水则会形成以水井为中心的高渗透性开启大裂缝或快速水流通道[22]，并指向采油井方向[23-24]，形成由诱导裂缝沟通形成的致密油藏水窜通道。假设若干条沟通的裂缝构成了注采井间的裂缝网络。通过分析井间沟通裂缝的分布特征，明确单条裂缝和井间裂缝网络的形态特征。

1)井间沟通裂缝可近似为二叉树模型。

由于储层改造和高压注入，近井地带裂缝发育且开度较大，井间地带裂缝开度较小，井间沟通裂缝形态类似“从树干逐渐扩展到连接的树枝”[13，25]。因此可选用二叉树模型描述井间沟通裂缝形态，二叉树模型中每级裂缝单元的分叉角度、开度比、长度比和纵横比为常数[26]。在高压控制下，当裂缝交点的流体压力大于作用在天然裂缝面上的正应力时，天然裂缝将发生膨胀，使裂缝暂时偏离垂直最小主应力方向[27]。裂缝延伸方向和垂直最小主应力方向形成交叉，构成一个二叉树结构[28-29]。鄂尔多斯盆地王窑区延长组的高角度天然裂缝在平面上呈雁列式排列，相邻的两条裂缝之间有较小的间距，单条裂缝在平面上的伸展长度有限，连通关系近似二叉树裂缝[20]。

2)井间沟通裂缝的开度近似服从对数正态分布。

受储层本身性质及应力大小的影响，井间沟通裂缝之间开度的差异较大。矿场中采油井见水时间和水淹类型各不相同[30]，也间接证明了开度的差异性。为描述井间沟通裂缝开度的分布，统计学是一个首选的方法[31]。自1997年SPE和SEC联合颁布规定承认概率法储量评估结果以来，概率法目前已被国内外很多石油公司采用[32]。在地质统计和砂岩储层渗透率分布规律研究中，普遍认可小层渗透率符合对数正态分布[33]。由于裂缝的渗流能力实际由裂缝的张开程度决定，因此也可认为井间沟通裂缝的开度服从对数正态分布。

3)井间沟通裂缝是高角度的且贯穿注采井间。

由于致密储层的岩石脆性程度大，在应力场的作用下容易产生高角度裂缝[1]。例如鄂尔多斯盆地安塞南部地区，构造挤压作用在岩石中形成了大量的高角度裂缝。高压注水下高角度裂缝开启，并在最大主应力方向延伸，形成近乎垂直且延伸规模大的井间裂缝网络。

4)井间沟通裂缝贯穿储层，高度为储层厚度。

野外露头、岩心观察及实验分析表明，在碎屑岩能干层与非能干层互层(如砂泥岩互层)的地层中，不同岩性层对应不同的岩石力学层，裂缝大多数终止于层面[27]。

综上，致密油藏水驱井间裂缝网络近似为高角度、延伸长、贯穿储层和开度服从对数正态分布的二叉树裂缝模型。单条井间沟通裂缝由一对二叉树裂缝组成(图1a)，单个二叉树裂缝中(图1a单侧部分)包含m级裂缝单元，即二叉树裂缝的深度为m。第i级裂缝单元的开度、高度和长度分别为bi、hi、li，且裂缝开度bi是服从对数正态分布的随机变量。井间裂缝网络由n组二叉树裂缝对组成(图1b)，第1级裂缝单元由n条井间沟通裂缝组成，开度为nb1。

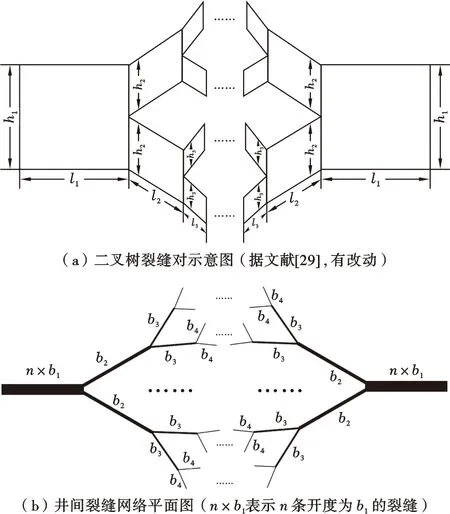
图1 井间裂缝网络物理模型示意图(注采井位于两侧)

1.2 井间裂缝网络的假设

基于井间裂缝网络由若干组二叉树裂缝组成的物理模型，建立注入水在井间裂缝网络中流动的假设条件。

1)注采井间由二叉树裂缝对沟通，二叉树裂缝对由2条二叉树裂缝相对组成(图1a)，n条二叉树裂缝对组成井间裂缝网络(图1b)。

2)二叉树裂缝中每级裂缝单元开度是随机变量，服从对数正态分布。

3)二叉树裂缝中每级裂缝单元的分叉角度、开度比、长度比和纵横比为常数。

4)每组二叉树裂缝对的两端压差相等。

5)采油井定液量生产，其产水量包括井间裂缝网络产水和基质产水。

6)井间裂缝网络的流动中，忽略油水流度差异和重力、毛管力作用。

2 二叉树裂缝开度概率密度函数和等效渗透率

物理模型中假设井间裂缝网络由若干组二叉树裂缝组成，且二叉树裂缝的开度是服从对数正态分布的随机变量。因此，建立二叉树裂缝开度的概率密度函数和等效渗透率表达式，为后续井间裂缝网络产水模型推导提供参数方程。

2.1 二叉树裂缝开度概率密度函数

根据假设条件(2)，二叉树裂缝每级裂缝单元的开度皆服从对数正态分布。实际储层中，裂缝开度存在最小值0和最大值bmax，即在(0，bmax]内累积概率为1。在区间(0，bmax]内归一化对数正态分布的概率密度函数，得到二叉树裂缝开度的概率密度函数f(b)。

(1)

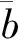
2.2 二叉树裂缝渗透率表征

由于二叉树裂缝对是对称结构，选取单条二叉树裂缝建立渗透率表达式。首先分别求取二叉树裂缝两端压差、平均渗流面积，然后利用达西定律得到二叉树裂缝的等效渗透率表达式。

1)二叉树裂缝空间形态表征。

对于单条二叉树裂缝(图1a单侧部分)，其深度为m，第i级裂缝单元的开度、高度和长度分别为bi、hi、li。根据假设条件(3)，二叉树裂缝开度比、长度比和纵横比系数可表示为

β=bi+1/bi

(2)

γ=li+1/li

(3)

λ=hi/bi

(4)

式(2)～(4)中：β、γ、λ分别为二叉树裂缝的开度比、长度比和纵横比，为常数；bi+1、bi分别为第i+1、i级裂缝单元的开度,i=1,2,…,m;m为二叉树裂缝的深度；li+1、li分别为第i+1、i级裂缝单元的长度；hi为第i级单元的裂缝高度。

因此，第i级裂缝单元的开度、高度和长度均可以由第1级裂缝单元的参数表示。

bi=b1βi-1

(5)

hi=λb1βi-1

(6)

li=l1γi-1

(7)

式(5)～(7)中：b1、l1分别为第1级单元的裂缝开度、长度。

2)二叉树裂缝两端压差表征。

二叉树裂缝由m级裂缝单元组成，第i级裂缝单元压差Δpi之和即为二叉树裂缝两端压差Δpt。考虑第i级裂缝单元的粗糙度和迂曲度，将第i级裂缝单元的渗透率Ki表示为

(8)

式(8)中：Ki为第i级单元的裂缝渗透率；c为粗糙度和迂曲度对裂缝渗透率的影响系数，取0.75[34]。

当单条二叉树裂缝中流量为q时，由于第i级单元中共有2i-1条裂缝(i=1,2,…,m)，则可根据物理模型假设条件(4)～(6)，利用达西定律和式(8)将第i级单元两端对应压差Δpi表示为

(9)

式(9)中：Δpi为单条二叉树裂缝中第i级裂缝单元两端的压差；负号表示消耗；q为单条二叉树裂缝中的流量；μ为二叉树裂缝中流体平均黏度。因此，单条二叉树裂缝两端的压差Δpt可表示为

(10)

式(10)中：Δpt为单条二叉树裂缝两端的压差。

3)二叉树裂缝平均渗流截面积表征。

首先求取二叉树裂缝总体积V与总距离l，然后利用二者之商构造二叉树裂缝平均渗流截面积。第i级单元中共有2i-1条裂缝(i=1,2,…,m)，单条二叉树裂缝第i级裂缝单元的体积Vi可表示为

(11)

式(11)中：Vi为单条二叉树裂缝第i级裂缝单元的体积。因此，单条二叉树裂缝的总体积V可表示为m级裂缝单元体系的总和。

(12)

式(12)中：V为单条二叉树裂缝的总体积。

如图1b所示，二叉树裂缝的第1级裂缝单元沿注采方向，其他裂缝单元与注采方向存在夹角，所以二叉树裂缝的总距离l可表示为第1级单元长度与其他单元长度之和。

(13)

式(13)中：l为单条二叉树裂缝的总距离；θ为二叉树裂缝分叉角度(θ<90°)，为常数。

根据体积相等原则，单条二叉树裂缝的平均渗流截面积A可表示为总体积V与总距离l之商。

(14)

式(14)中：A为单条二叉树裂缝的平均渗流截面积。

4)二叉树裂缝等效渗透率表征。

将二叉树裂缝两端压差Δpt、总距离l和平均渗流截面积A代入达西定律，得到单条二叉树裂缝等效渗透率K的表达式。

(15)

式(15)中：K为单条二叉树裂缝的等效渗透率。如式(15)所示，二叉树裂缝等效渗透率K是第1级裂缝单元开度b1、二叉树裂缝分叉角度θ、开度比β、长度比γ、二叉树裂缝级数m的函数。当二叉树裂缝退化为单条平板缝，即m=1、c=1时，式(15)退化为立方法则。

令X为式(15)中包含裂缝渗透率影响系数c、二叉树裂缝分叉角度θ、开度比β、长度比γ和二叉树裂缝深度m的参数团，则单条二叉树裂缝的等效渗透率K可表示为修正的立方法则形式。

(16)

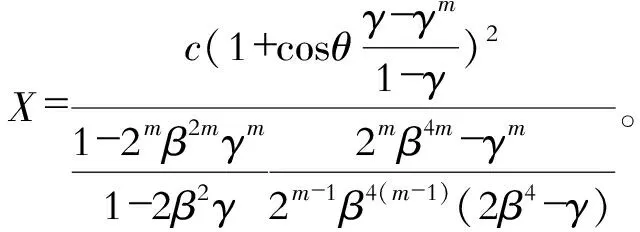
3 井间裂缝网络反演模型和方法

3.1 数学建模

1)井间裂缝网络产水量模型。

如假设条件(2)所述，二叉树裂缝第1级裂缝单元开度b1是服从对数正态分布的随机变量，定义域为(0，bmax]。所以，第1级裂缝单元开度值为b的裂缝条数应为nf(b)，横截面积为nf(b)hb。第1级裂缝单元开度为b的二叉树裂缝的总产水量可表示为

(17)

式(17)中：q(b)为第1级裂缝单元开度为b的二叉树裂缝总产水量；n为井间诱导裂缝总条数；h为裂缝高度；Δp为注采压差；L为注采井距。

水驱过程中，注入水将首先沿开度最大的裂缝到达采油井井底，然后依裂缝开度大小依次到达采油井井底，使得采油井产水量逐渐增大。在采油井见水后的时刻t，假设第1级裂缝单元开度大于b(t)的裂缝已完全被注入水占据。对第1级裂缝单元开度大于b(t)的裂缝产水量求和，可得到见水后井间裂缝网络总产水量Qw(t)。

(18)

式(18)中：Qw(t)为采油井见水后井间裂缝网络在时刻t的总产水量；t为注水时间，t=0为开始注水的时刻；t1为采油井含水开始上升的时刻；bmax、b(t)分别为被注入水占据的裂缝中第1级裂缝单元最大开度、时刻t被注入水占据的裂缝中最小的第1级单元开度。

(19)

(20)

裂缝开度b是连续型随机变量，将概率密度函数代入式(18)并在裂缝开度范围内作积分，得到见水后井间裂缝网络总产水量模型。

(21)

2)采油井理论含水率模型。

基于假设条件(5)，令采油井产液量为Q。利用井间裂缝网络总产水量Qw(t)与采油井产液量Q之商，得到采油井见水后理论含水率的数学表达式。

(t≥t1)

(22)

式(22)中：fw(t)为采油井见水后t时刻的理论含水率；fw0为油藏初始含水饱和度对应的含水率，fw0=Qw0/Q；Qw0为采油井产出的地层水量，为常数；Q为采油井产液量。

利用泰勒级数、误差函数性质和换元法，t时刻采油井见水后理论含水率的解析表达式可表示为

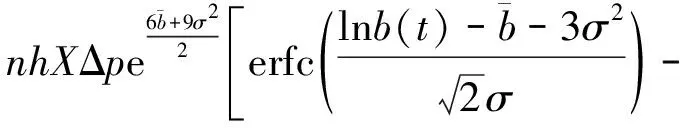
(23)

式(23)中：efrc()为互补误差函数。

3)限制条件。

根据裂缝开度和含水率的物理意义，采油井理论含水率模型的限制条件应包括：①裂缝开度的期望和方差大于0且期望小于bmax；②理论含水率在(fw0，1]内。

裂缝开度b的期望E(b)和方差D(b)恒大于0，所以限制条件①对应不等式如式(24)所示。

(24)

(25)

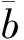
(26)

3.2 井间裂缝网络参数影响规律分析

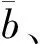
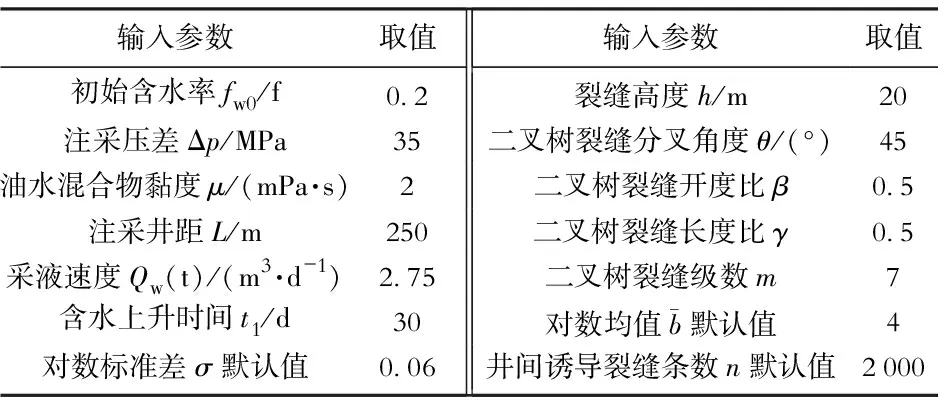
表1 敏感性分析基础数据表

1)第1级裂缝单元开度的对数标准差影响规律。

当第1级裂缝单元开度的对数标准差σ从0.02增至0.10，对应理论含水率曲线如图2所示。随着σ增大，理论含水率的上升形状逐渐变缓，最大含水率有较小幅度上升。当裂缝开度的对数标准差σ增大时，裂缝开度服从的对数正态分布变得平缓(图3)，裂缝开度分布范围变广，因此理论含水率上升速度变缓。同时，根据裂缝开度期望E(b)的定义式(式(24))，σ增大时E(b)存在较小幅度的增加，导致最大含水率略有上升。

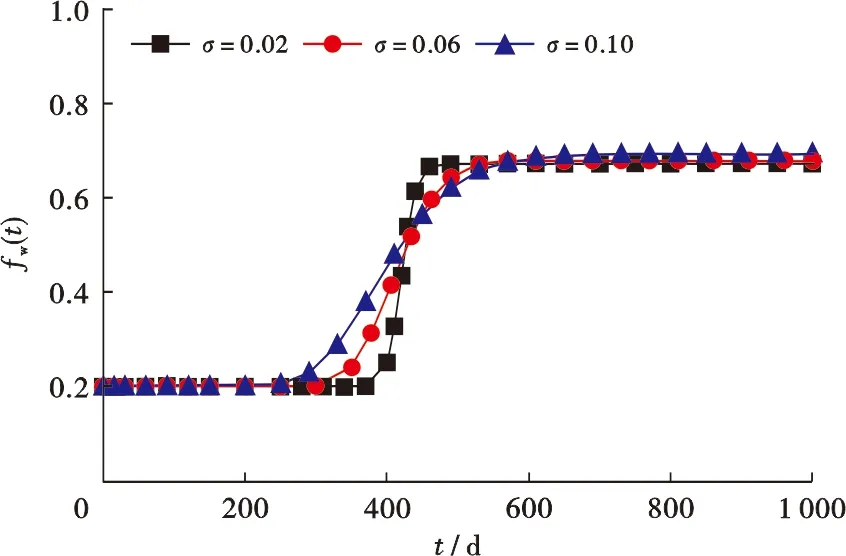
图2 第1级裂缝单元开度取不同对数标准差时得到的理论含水率曲线

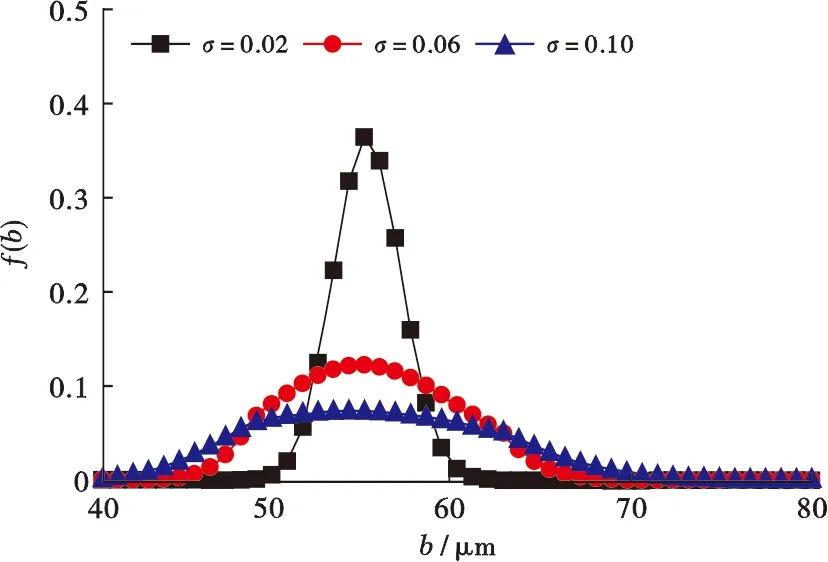
图3 第1级裂缝单元开度取不同对数标准差时得到的概率分布

2)第1级裂缝单元开度的对数均值影响规律。

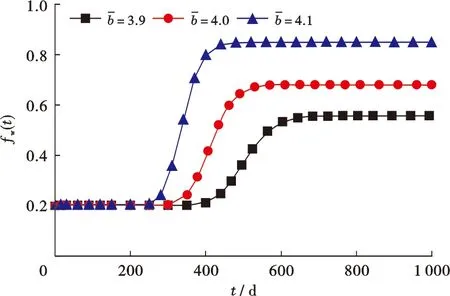
图4 第1级裂缝单元开度取不同对数均值时得到的理论含水率曲线

3)井间诱导裂缝条数n影响规律。

当井间诱导裂缝条数n从1 000增至3 000，对应理论含水率曲线如图5所示。随着n增大，理论含水率的最大值单调递增。这是由于当n增大时，井间裂缝网络内产水流量对应增加，从而最大含水率上升。

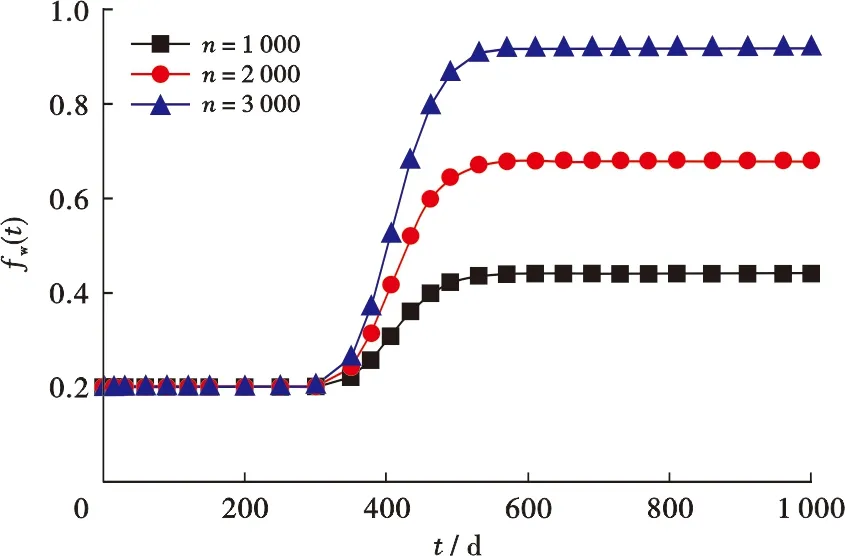
图5 取不同井间诱导裂缝条数时得到的理论含水率曲线

3.3 井间裂缝网络参数反演次序确定

影响规律分析结果显示，裂缝开度的对数标准差σ主要影响含水率曲线的上升形状，裂缝开度的对数均值主要影响含水率曲线的上升时间和最大值，井间诱导裂缝条数n主要影响含水率曲线的最大值。因此，推荐的井间裂缝网络参数反演次序为：首先调整裂缝开度的对数标准差σ拟合上升形状，然后调整裂缝开度的对数均值拟合上升时间，最后调整井间诱导裂缝条数n拟合最大值。上述参数反演次序基本实现了曲线特征与反演参数的一一对应，能大幅降低反演方法的多解性。

4 算例应用结果与分析

4.1 井间裂缝网络参数反演结果

1)井间裂缝网络参数反演。

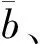
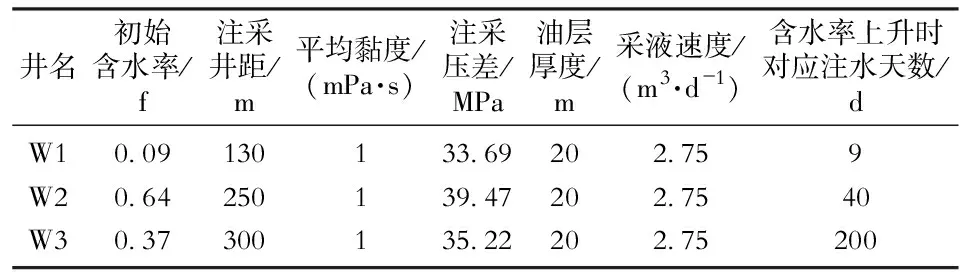
表2 井间裂缝网络参数反演基础数据

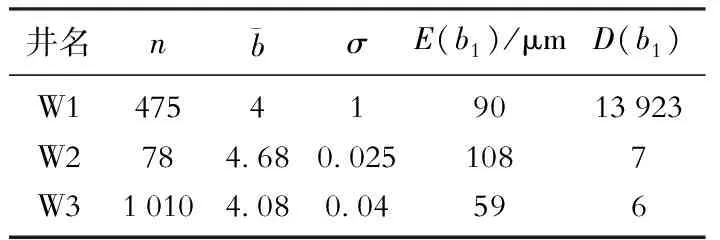
表3 井间裂缝网络特征参数量化结果

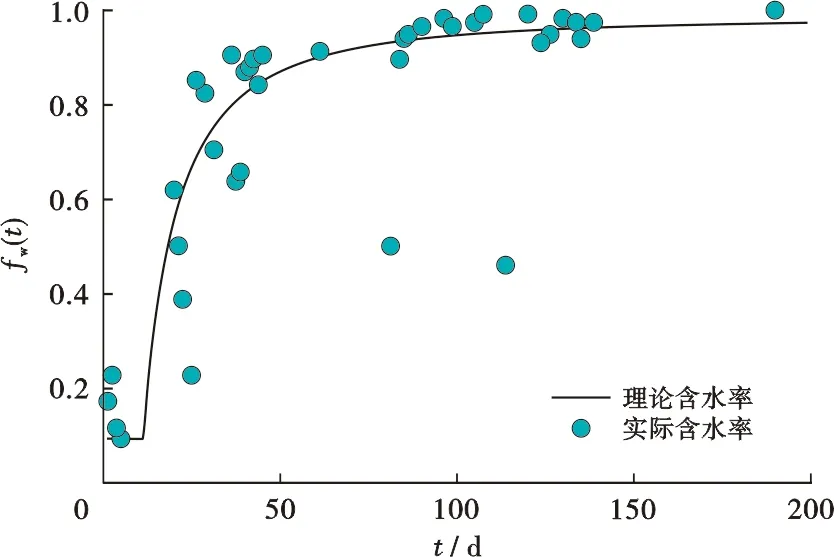
图6 W1井含水率拟合曲线

2)反演结果多解性分析。

井间裂缝网络反演的多解性一般来自两处，一是二叉树裂缝参数的不确定性，二是含水率曲线拟合时的多解性。在含水率曲线拟合中，推荐的参数反演次序已经大幅降低了拟合过程的多解性。因此，二叉树裂缝参数的不确定性是反演多解性的主要原因。

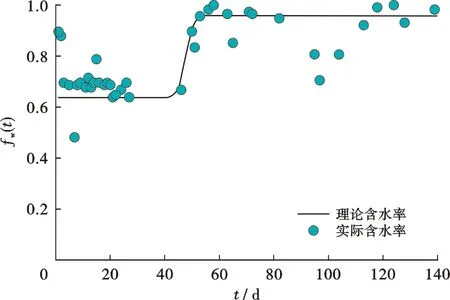
图7 W2井含水率拟合曲线

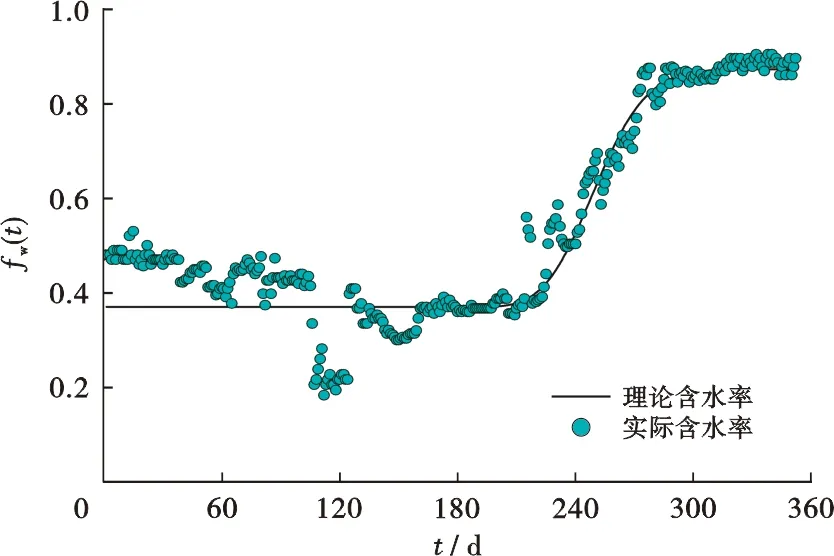
图8 W3井含水率拟合曲线

以W2井为例，分析不同二叉树裂缝参数时反演结果的变化情况。若二叉树裂缝开度沿井距变化较小，即每级裂缝单元的开度接近时，例如裂缝开度比β=0.8、长度比γ=0.8、裂缝级数m=22、分叉角度θ=45°，采用推荐的反演次序，得到井间裂缝网络参数如表4所示。W2井对应井间裂缝网络参数反演结果显示(表3、4)，当井间二叉树裂缝各级单元开度变得接近时，W2井对应的第1级裂缝单元平均开度E(b)从108 μm降至12 μm，二叉树裂缝条数从78条增至750条，对近井地带裂缝的认识从大缝降至中缝。

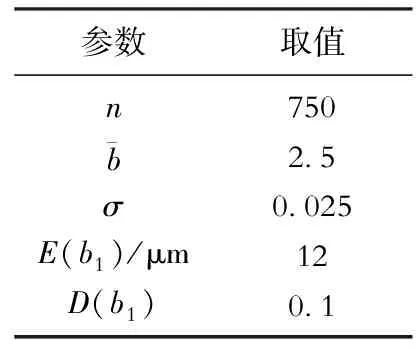
表4 二叉树裂缝单元开度接近时量化结果

致密储层中，近井地带往往存在压裂缝沟通或高压注入沟通的裂缝网络，井距中部地带未被压裂等措施改造且压力梯度整体较低，因此可认为井间诱导裂缝开度沿井距变化较大，即表1中的二叉树裂缝参数相对合理、表3中反演结果更为可信。

4.2 近井地带裂缝分布特征分析

以第1级裂缝单元为代表，分析3口单井近井裂缝开度分布区间、半长和裂缝级别。利用反演得到的裂缝特征参数，计算得到了第1级裂缝单元开度期望、分布区间和长度，并和试井、调剖动态进行了对比验证(表5)。结果显示，W1、W2和W3井的近井地带分别发育小缝—大缝、大缝和中缝。

表5 第1级裂缝单元参数分析结果

1)近井井间裂缝开度分布特征。

利用反演结果(表3)和概率密度函数(式(1))，分别计算得到W1、W2和W3井对应的第1级裂缝开度概率(图9a)和对应条数分布(图9b)。以裂缝开度对应条数不小于1条作为区间截断标准，得到3口单井第1级裂缝开度分布区间依次为[3,175]、[102,114]和[52,67](单位为μm)，区间距离依次为173、13、16 μm，区间距离的大小关系和含水率上升持续时间长短吻合。反演得到的3口单井第1级裂缝开度对数标准差依次为1、0.025、0.04，对应含水率上升阶段持续时间分别为90、10、80 d。结果显示裂缝开度对数标准差越大，含水率上升阶段越长。究其物理原因，裂缝开度对数标准差越大时，裂缝开度分布范围越广，注入水沿着裂缝到达采油井底的时间差异越大，因此表现出含水率上升阶段持续更久。

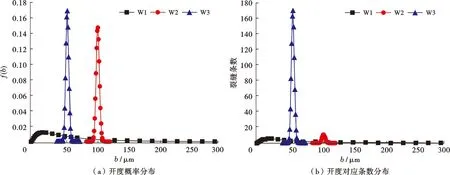
图9 反演得到的W1、W2、W3井第1级裂缝单元开度概率和对应条数分布

2)近井地带裂缝半长分析。

根据如图1a所示的二叉树裂缝对，二叉树裂缝长度为井距之半。利用式(13)，得到第1级裂缝单元长度l1表达式。

(27)

计算得到W1、W2和W3井对应的第1级裂缝单元长度分别为38.3、73.7、88.4 m，是井距的0～29.5%，显示注采井距的两端各1/3段可能存在中—大缝，这与试井解释得到的裂缝半长35～88 m基本吻合。

3)近井地带裂缝级别判断。

W1、W2、W3井第1级裂缝单元开度分别服从对数均值4.00、4.84、4.26和对数标准差1.00、0.025、0.05的对数正态分布，对应第1级裂缝单元开度期望分别为90、108、59 μm，符合试井和调剖施工反映的特征。W1试井解释成果显示，近井缝网裂缝平均渗透率2.65 mD，是储层平均渗透率的153倍；W2单井调剖时可以2 m3/h注入约200 m3强化冻胶。上述结果显示近井渗流条件得到了大幅度的改善，近井存在中缝—大缝网络。

结合三口单井第1级裂缝开度分布区间[3,175]、[102,114]和[52,67](单位为μm)，综合判断W1、W2和W3井的近井地带分别发育小缝—大缝、大缝和中缝。

4.3 井间裂缝网络分布特征分析

结合井间裂缝网络反演结果(表3)，分析W1和W2井对应的井间裂缝分布特征。结果显示，W1井水窜方向对应的井间通道主要由较高注采压差导致的诱导裂缝组成，W2水窜方向对应的井间通道由发育的天然裂缝和较高的注采压差形成(表6)。

表6 井间裂缝网络参数分析结果

W1井第1级裂缝开度最小、最为分散(图9a黑线)，裂缝总条数为475条(表3)，显示W1井由一簇开度整体较小但分布区间广，裂缝条数数量中等的井间裂缝网络沟通至注水井。裂缝开度概率分布显示W2井第1级裂缝开度最大、最为集中(图9a红线)，且裂缝总条数最少(表3)，说明W2井由一簇裂缝开度较大且分布区间小，裂缝数量较少的井间裂缝网络沟通至注水井。

综合判断，W1井对应井间裂缝开度整体偏小且差异大，裂缝条数较多，推测井间裂缝网络主要由较高的注采压差形成；W2井对应井间裂缝开度整体偏大且差异小，裂缝条数较少，结合井间天然裂缝发育的地质特征，井间裂缝网络由发育的天然裂缝和较高的注采压差形成。

4.4 讨论

1)反演多解性的消除。

多解性是反演方法难以避免的难题，得到准确的二叉树裂缝参数是消除井间裂缝反演多解性的核心难题。为解决该难题，一方面可以直接开展井间诱导裂缝延伸的研究，将近井裂缝延伸的实验研究拓展至井间裂缝，从理论上完善二叉树裂缝对形态的物理模型；另一方面可以尝试在反演时引入井间注采压差的限定，二叉树裂缝参数控制裂缝等效渗透率，从而影响井间裂缝网络两端的注采压差，因此在反演中引入注采压差，有望消减裂缝参数的多解性。

2)反演参数应用的设计。

反演得到的井间诱导裂缝条数和第1级裂缝单元长度、开度均值，可用于致密储层调剖堵水选井选剂和用量设计。根据第1级裂缝单元开度均值，可选取匹配药剂封堵能力的单井。根据第1级裂缝单元长度、开度均值，可进行药剂强度和微球粒径、水化膨胀速度的优选；根据井间诱导裂缝条数和第1级裂缝单元长度、开度均值，可进行药剂用量设计。

5 结论

1)井间裂缝网络可近似为若干组开度服从对数正态分布的二叉树裂缝对，二叉树裂缝等效渗透率可由修正的立方法则表示，为二叉树第1级裂缝单元开度b1，二叉树裂缝分叉角度θ、开度比β、长度比γ、二叉树裂缝级数m的函数。

2)3口现场单井的应用结果表明，第1级裂缝单元开度期望分别为90、108、59 μm，致密储层近井地带存在中缝—大缝，范围约为注采井距的两端各1/3段；不同的井间裂缝网络参数差异较大，与天然裂缝发育程度有关。

3)得到的裂缝网络参数能够为调堵设计提供依据，其反演多解性主要来自二叉树裂缝参数的不确定。研究井间裂缝延伸形态和引入注采压差限定，有望得到更准确的井间裂缝网络参数。