卫星导航系统星载钟时域频率稳定度探讨

董 哲，陈汗龙，欧阳文，周 鑫

卫星导航系统星载钟时域频率稳定度探讨

董 哲，陈汗龙，欧阳文，周 鑫

（中国人民解放军32034部队，成都 610500）

介绍了四大卫星导航系统采用的时间系统，分析了频率标准的时域频率稳定度研究内容、研究方法，推导了其实用计算方法和公式，主要对近十年以来研究GNSS星载原子钟频率稳定度的测算数据进行了梳理和归纳总结，对比分析了各个导航系统星载原子钟的频率稳定度，综合数据表明大部分星载钟天稳均可达到10-14量级，其中GPS星载铷钟和Galileo星载PHM钟稳定性最好。

卫星导航系统；原子钟；阿伦方差；频率稳定度

0 引言

时间是自然界七大基础物理量之一，是描述物体运动的基础[1]。在卫星导航系统中，时间信息的产生、保持和测量是实现授时、定位、导航及测速等服务的前提，可以说卫星导航定位原理的本质是测时间，有了精准的时间基础才能测算出准确距离、位置信息。一个时间系统的建立必须具备可观测到的周期性运动，其次该周期运动应具备稳定性、连续性和复现性，简单地说，时间系统的建立需要包括时间原点（起始历元）和时间单位（尺度）。为了给卫星导航系统提供连续、稳定的时间基准，当前全球四大卫星导航系统根据国际原子时的基本定义建立了各自的时间系统[2-5]，如表1所示。

卫星导航系统的时间系统主要由主控站、监测站和星载的原子钟共同建立和维持，时间尺度均由系统内部原子钟通过加权算法综合计算得出。星载原子钟是卫星导航时间系统的重要组成部分，它的稳定性与卫星钟差模型的建立紧密联系，直接关系用户定位、授时解算的准确性，有必要对星载原子钟频率稳定度进行综合分析和探讨。

表1 卫星导航系统所采用的时间系统

1 频率稳定度

频率标准是指能产生高准确度和高稳定度的标准频率信号的振荡器及附属电路，衡量频率标准质量的技术指标包括频率准确度、频率偏差、频率稳定度、频率漂移率、重现性、开机特性、频率调范围和分辨率、外部特性等内容[6]，如图1所示。

通常，不同频率标准根据其自身特点做相适应的平台应用，如计量、通信、科研等，其中最常见的频率标准为高稳石英晶体频率标准和原子频率标准两类[3]，卫星导航系统用的后者，由高精度原子钟产生并输出频率信号。分析卫星导航系统原子钟的性能，就是分析原子钟（星载和地面）产生的高精度原子频标，在实际应用研究中通常选取频率准确度、频率漂移率和频率稳定性作为原子频标主要的评价指标。

频率稳定度的定义为：受系统内部电路噪声和系统外部环境的影响，频率标准的输出信号不是固定值，而是在一定范围内变化，频率稳定度用来描述频标输出频率受随机噪声影响程度的大小[6]。频率稳定度表征了原子钟输出信号和授时的稳定性，用于衡量原子钟维持在特有频率的能力，常用中短期频率稳定度作为评价指标，对星载原子钟的实时性能进行分析和评价。例如国际上对卫星钟差的模型主要是通过式（1）来建立的；

1.1 时域频率稳定度研究内容

频率标准的输出信号常用式（2）表示：

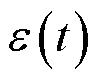
根据瞬时角频率是相位时间导数关系，得：

可得出瞬时相对频率起伏公式为：

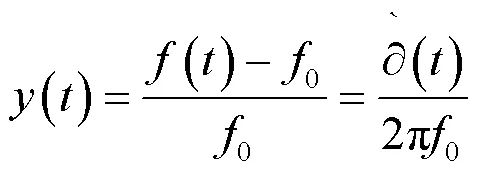
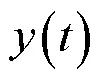
1.2 时域频率稳定度研究方法

在时域频率稳定度分析方法上，有标准方差、阿伦方差、重叠阿伦方差、改进阿伦方差、改进总方差、哈达玛方差、重叠哈达玛方差、哈达玛总方差等[6-8]方法。其中，美国学者阿伦（D.W.Allan）提出的阿伦方差成为了最常用、实用的时域频率稳定度分析方法，它解决了用标准方差描述频标稳定度过程中存在的线性发散问题，使得测量次数越多，求得频率稳定度结果越精确。

广义上的阿伦方差表达式为：

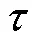
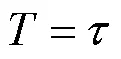
式（9）要求测量组数为无穷多，而实际工程应用中无法达到，所以常采取估算值，即：

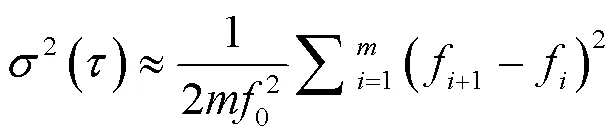
在实际工程应用中，由于瞬时频率难以测量，且噪声对频率标准输出频率的干扰往往表现在对输出信号相位上的干扰，因此，常利用时间间隔计数器，通过比相法或比时法进行时域频率稳定度的测算，如式（11）所示：

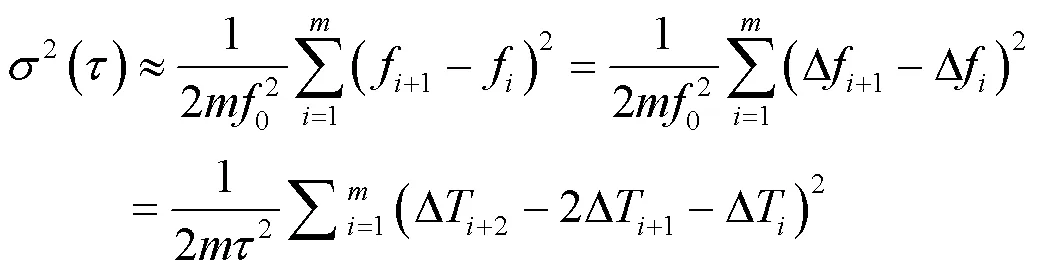
2 星载原子钟频率稳定度测算综述

主要对2010年以来研究星载原子钟稳定度的文献进行了梳理和归纳总结，因数据来源与测算时间的不同，对原子钟频率稳定度的测算结果会产生一些差异，但总体上能发现一些共性的规律和结果。

2.1 北斗卫星钟时域频率稳定度测算分析

北斗系统工程空间段的卫星星载原子钟多为铷钟[9]，包括地球静止轨道（Geosynchronous Earth Orbit，GEO）卫星钟、倾斜轨道同步（Inclined Geosynchronous Satellite Orbit，IGSO）卫星钟、中轨地球（Medium Earth Orbit，MEO）卫星钟。

韩春好[10]在2013年采用星地无线电双向时间比对法对北斗在轨卫星星载原子钟进行时域频率稳定度测算，得到北斗卫星钟稳定性维持在10-14量级，其中天（1 day）频率稳定度可达2.53～9.38E-14。

王宇谱[11]采用2013～2015年共3年多的多星定轨联合解算的BDS卫星钟差数据，利用重叠哈达玛方差分析了北斗星载原子钟的长期频率稳定度，得到在3年间星载钟的天稳平均值：GEO卫星钟为1.283E-13，MEO卫星钟为1.385E-13，IGSO卫星钟为1.765E-13，其中IGSO卫星钟频率稳定度最差。

田婕[12]采用2014年15天的北斗精密钟差文件，利用重叠哈达玛方差对北斗在轨卫星钟的频率稳定度进行分析，得到千秒稳定度均值为1.82E-13，万秒稳定度均值为1.09E-13，天稳定度平均值为1.11E-13，其中GEO卫星钟的万秒稳定度较差。

艾青松[8]利用武汉大学2015～2016年公布的北斗卫星5min采样的钟差产品，按照GEO、IGSO和MEO三种星载原子钟类型进行了时域频率稳定度的测算分析，结果表明北斗卫星钟存在明显的频率漂移现象，各类星载钟的万秒稳定度维持在10-13量级，相差不大，在天（1 day）稳定度上从高到低分别是MEO卫星钟、IGSO卫星钟、GEO卫星钟。

王省超[13]利用德国地学中心在2016～2017年间，发布的共456天事后精密钟差产品，对北斗卫星钟的稳定性进行了测算分析，统计结果可以看出，MEO卫星钟的稳定性（万秒稳和天稳）略优于IGSO卫星，GEO卫星最差。

王天[14]利用2013年4月份国内的7个跟踪站和8个境外站的接收机对北斗系统的14颗在轨卫星进行观测，结果表明MEO卫星钟和GEO卫星钟天稳较好，其均值能够达到9.62E-14和7.38E-14，IGSO卫星钟较差。

上述研究表明，北斗系统星载原子钟的千秒稳都可达到10-13量级，万秒稳和天稳上MEO铷钟表现较优，均可达到10-14量级，GEO和IGSO铷钟介于10-13～10-14量级之间，GEO铷钟天稳上大部分可达到10-14量级，整体而言MEO星载钟的稳定度在系统中最优，其次是GEO和IGSO卫星钟。如表2所示。

表2 北斗系统星载原子钟频率稳定度测算

2.2 GPS卫星钟时域频率稳定度测算分析

郭海荣[7]对GPS卫星的Rb钟和Cs进行了时域频率稳定度的测算，为了去除频率漂移率对阿伦方差估算值的影响，他分别计算了去除频率漂移前后的阿伦方差值，最后得出GPS的BlockⅡA的铷钟（PRN06）、BlockⅡA的铯钟（PRN10）、BlockⅡR的铷钟（PRN16）天（1 day）稳定度分别为3.5E-14、8.5E-14和1.0E-14，比较分析表明BlockⅡR的Rb钟的频率稳定度最好，BlockⅡA的铯钟短期频率稳定度不如铷钟，若6 h不对铯钟进行修正，此时测距误差可增加0.5 m左右。

Francine Vannicola[15]采用6个USAF站，11个NGA站和2个IGS站组成的监测网络，分别对BlockⅡF的铯钟（SVN62/PRN25）、BlockⅡF的铷钟和BlockⅡR的铷钟进行测算，分别得到天（1 day）频率稳定度为5E-14，7E-15和9E-15。

贾小林[16]用Hadamard方差对GPS星载原子钟性能指标进行了分析，给出了30颗星载钟性能指标，结果表明BlockⅡR铷钟天稳整体优于其他星载钟，大部分BlockⅡR 铷钟天稳可达到1～3E-14的水平。

艾青松[8]选取IGS发布的2016～2017年间共425天采样间隔为5 min的钟差产品，分别对GPS在用的卫星钟时域频率稳定进行测算，得到大部分原子钟天稳定度都在10-15量级，同时原子钟时域频率稳定性由高到低分别为BlockⅡF 铷钟、BlockⅡRM 铷钟、BlockⅡR 铷钟和BlockⅡF 铯钟。

田婕[12]采用2014年15天的GPS精密钟差产品作为原始数据，在对数据进行预处理后，计算得到GPS星载原子钟的万秒稳定度均值为9.53E-14，天稳定度均值为3.18E-14，其中BlockⅡF铷钟的天文均值为2.72E-15，比均值高一个数量级，整体上铷钟稳定度优于铯钟。

学者研究表明，GPS星载钟在千秒稳可达到10-13量级，绝大多数星载钟在万秒稳、天稳上可达到10-14量级，部分星载钟在天稳上甚至可以达到10-15量级，其中ⅡF铷钟最优，ⅡA铷钟、ⅡR铷钟和ⅡRM铷钟表现其次，GPS铯钟的稳定度指标明显低于铷钟，如表3所示。

表3 GPS星载原子钟频率稳定度测算

2.3 GLONASS与Galileo卫星钟时域频率稳定度测算分析

艾青松[8]利用俄罗斯空间局分析中心（Information and Analysis Center，IAC）发布的5 min钟差产品对GLONASS卫星钟时域稳定度进行分析，结果表明它的卫星钟千秒稳、万秒稳和天稳的均值分别为3.50E-13、1.28E-13和4.78E-14，绝大部分天稳达到了10-14量级；利用GBM发布的5 min MGEX钟差产品对Galileo卫星钟时域稳定度进行分析，结果表明各原子钟的千秒稳和万秒稳达到了同一水平，都在10-14量级，部分甚至达到了10-15量级，整体性能来说PHM钟优于RAFS钟。

赵丹宁[17]利用欧洲定轨中心公开发布的2018～2019年的300 s采样间隔的GLONASS事后精密卫星钟差数据对星载钟的稳定度进行分析，发现其天稳在10-13至10-14量级之间，均值为4.918E-14。

丁毅涛[18]利用GBM、ISC和WUM发布的5 min采样间隔数据对GLONASS和Galileo卫星钟的稳定度进行分析，发现其天稳均达到了10-14量级。

韩有文[19]利用德国地学研究中心（German Research Centre for Geosciences，GFZ）在2018年发布的19天精密钟差产品，对Galileo星载钟的稳定度进行了测算，发现PHM钟和RAFS星钟的天稳均达到了10-15量级。

潘雄[20]利用GFZ在2018～2019年发布的628天精密钟差产品，对Galileo星载钟的稳定度进行了分析和计算，结果表明Galileo星载钟有较高的频率稳定度，所有星载钟万秒稳均值为3.12E-14。

综合分析结果可以看出，GLONASS与Galileo星载钟频率稳定度在天稳上都可达到10-14量级，Galileo PHM钟表现更优，不仅在天稳可以达到10-15量级，在万秒和千秒稳也都达到了10-14量级，如表4所示。

表4 GLONASS与Galileo星载原子钟频率稳定度测算

2.4 星载原子钟稳定性比对结果分析

当前对GNSS星载钟频率稳定度研究数据表明：

1）千秒稳定度上，四个导航系统相差不大，都可达到10-13量级，其中GPSⅡF铷钟、Galileo PHM钟性能最好，可达到10-14量级；

2）万秒稳定度方面，北斗MEO铷钟、IGSO铷钟、GPS铷钟和Galileo PHM钟都处于10-14量级，而北斗GEO铷钟和GPS铯钟表现较差，同处于10-13量级；

3）天稳定度方面，GPS与Galileo星载钟整体优势明显，都在10-14量级水平以上，部分甚至可达10-15量级，而北斗星只有MEO星载钟可稳定在10-14量级，其余的星载钟天稳在10-13与10-14之间。

可以看出，卫星导航系统星载钟频率稳定度方面GPS星载钟整体最优，Galileo表现其次但优于GLONASS，而北斗GEO和IGSO星载钟还有一定差距。此外，GPSⅡF铷钟稳定性表现最好，千秒和万秒稳均在10-14量级，天稳可达到10-15量级。

3 结论

文章介绍了四大卫星导航系统采用的时间系统，对时间频率标准评价指标内容进行了说明，阐述了频率稳定度的基本概念，分析了频率标准的时域频率稳定度研究内容和研究方法，推导了其计算方法和公式，重点对近十年以来四大卫星导航系统星载原子钟频率稳定度的研究测算情况进行了梳理、分析和归纳总结，得到了相关结论。

[1] IEEE 1139-2008, 基本频率和时间计量学用物理量定义.随机不稳定性[S].2008.

[2] 曾庆化. 全球导航卫星系统[M]. 北京：国防工业出版社，2014：1-39.

[3] 魏浩瀚. 北斗卫星导航系统原理与应用[M]. 南京：东南大学出版社，2020：1-48.

[4] 高平. 导航卫星时频生成与保持技术研究[D]. 西安：西安电子科技大学，2011：12-25.

[5] 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安：长安大学，2012：25-55.

[6] 童宝润. 时间统一技术[M]. 北京：国防工业出版社，2004：17-88.

[7] 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州：解放军信息工程大学，2006：22-38.

[8] 艾青松. GNSS星载原子钟时频特性分析及钟差预报算法研究[D]. 西安：长安大学，2017：11-35.

[9] 翟造成，李玉莹. 下一代星载原子钟的新发展[J]. 全球定位系统，2010，35（5）：1-5.

[10] Han C, Cai Z, Lin Y, et al.Time Synchronization and

Performance of BeiDou Satellite Clocks in Orbit [J]. International Journal of Navigation&Observation, 2013:3-12.

[11] 王宇谱，吕志平，王宁. BDS星载原子钟长期性能分析[J]. 测绘学报，2017，46（2）：157-169.

[12] 田婕. GPS/BDS原子钟性能分析及钟差预报模型研究[D]. 西安：长安大学，2015：16-28.

[13] 王省超. 北斗卫星导航系统性能分析及应用研究[D]. 西安：长安大学，2018：8-26.

[14] 王天，王璐. 北斗导航系统卫星原子钟性能评估[J]. 测绘通报，2013（S1）：40-43.

[15] Vannicola F,Beard R,White J,et al.GPS Block IIF Atomic Frequency Standard Analysis[J].Proceedings of Annual Precise Time&Time Interval Systems&Applications Meeting, 2010: 1-12.

[16] 贾小林，冯来平，毛悦，等. GPS星载原子钟性能评估[J]. 时间频率学报，2010，33（2）：115-120.

[17] 赵丹宁. GLONASS星载钟性能分析[J]. 时间频率学报，2020，43（1）：66-71.

[18] 丁毅涛，郭美军. 基于不同机构钟差产品的GNSS星载钟性能分析与评估[J]. 时间频率学报，2020，43（1）：72-84.

[19] 韩有文. Galileo卫星星载原子钟性能分析[J]. 导航定位学报，2020，8（1）：54-58.

[20] 潘雄，杨玉锋，卿晨昕，等. Galileo在轨卫星钟性能评估与分析[J]. 中国惯性技术学报，2020，28（1）：53-59.

[21] 胡志刚. 北斗卫星导航系统性能评估理论与试验验证[D]. 武汉：武汉大学，2013：7-22.

[22] 孟祥广，孙越强，杜起飞，等. 北斗卫星在轨原子钟稳定性分析[J]. 大地测量与地球动力学，2016，36（7）：574-576+580.

Discussion on Time-Domain Frequency Stability of on-Board Clock in Satellite Navigation System

DONG Zhe, CHEN Hanlong, OUYANG Wen, ZHOU Xin

The time system adopted by the four major satellite navigation systems is introduced, the research content and research method of frequency standard time domain frequency stability are analyzed, and its practical calculation method and formula are deduced. The frequency stability of the satellite-borne atomic clocks of various navigation systems is compared and analyzed. The comprehensive data shows that most of the space-borne clocks can reach the order of 10-14. Among them, the GPS space-borne rubidium clock and Galileo The on-board PHM clock has the best stability.

Satellite Navigation System; Atomic Clock; Allan Variance; Frequency Stability

TN953

A

1674-7976-(2022)-04-251-07

2022-04-14。

董哲（1986.09—），山东梁山人，硕士，工程师，主要研究方向为卫星导航和时间频率。