地下水渗流作用下地下洞室块体稳定性分析

朱杰清

(中国电建集团福建省电力勘测设计院有限公司，福建 福州 350003)

0 引言

地下岩体中结构面的存在会直接降低围岩的强度[1-3]，岩体被不同尺度、产状的结构面切割形成的块体具有一定的随机性，从块体开挖揭露到通过计算判断块体的稳定性通常需要一定时间，在这段时间内若不及时采取措施，块体有可能失稳滑落，这给地下洞室工程的开挖过程带来不可预知的风险[4]。

地下洞室开挖后，围岩内部的应力场和渗流场发生耦合作用，地下水通过岩体内部的结构面向洞室方向渗流，经力学、物理及化学作用，易发生围岩失稳等问题[5-8]。因此，在研究地下洞室围岩稳定性的问题时，考虑地下水渗流作用十分必要。目前，许多学者针对这个问题进行了大量研究，并取得了一些成果。王明等[6]基于有限元数值方法得到裂隙岩体的渗流对地下洞室围岩稳定产生不利的影响；谷拴成等[7]应用等效分析方法研究渗流作用下锚杆支护巷道的稳定性，得到渗流作用时需要锚杆提供更大的支护力；李鹏飞等[8]讨论了渗流作用下海底隧道掌子面围岩的稳定性问题，发现渗流作用使得开挖面上部地层变形量明显大于下部。

本文依托某工程实例，利用极限平衡法和离散单元法进行模拟计算，分析洞室开挖过程中有无渗流作用下楔形体的稳定性，并分析两种方法的优缺点。

1 极限平衡法和离散元法基本原理

1.1 极限平衡法

极限平衡法是根据静力平衡原理分析不稳定块体的受力状态，以滑动面上阻滑力和下滑力间的比值(稳定系数)来评价块体稳定性。

计算方法如下所示：

(1)

式(1)中，F为稳定系数。

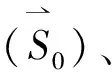
①脱离岩体

(2)

②沿单一结构面滑动

(3)

(4)

式(4)中，αi为结构面i的倾角，βi为结构面i的倾向。

③沿两条结构面滑动

(5)

不稳定块体的有效滑动方向按照表1的判据进行确定，满足其中的哪个判据就是不稳定块体的滑动方向，如果都不满足表1中的判据，则块体处于稳定状态。

表1 不稳定块体滑动方向判据及各结构面上的法向力

1.2 离散元法

离散单元法(简称DEM)是由Cundall在1971年首次提出，专门用来解决非连续介质问题的数值模拟方法。该方法把节理岩体看成由离散的岩块和岩块间的节理面组成，块体的几何形状取决于岩体结构中不连续面的空间位置及其产状，通过牛顿第二定律来表征块体的运动过程，并允许岩体的内部可以发生块体的大位移、旋转、滑动甚至块体的分离等运动，借此可以达到比较真实地模拟节理岩体中的非线性大变形特征。

3DEC离散元数值分析软件主要以离散单元法为基本理论来描述离散介质的力学行为，它将介质离散成为连续性特征(岩块)和非连续特征(结构面)两个基本元素的统一集合体，并通过成熟的力学定律来描述这些基本元素的受力变形过程。

2 实例计算

2.1 工程概况

某直墙圆拱型地下洞室开挖时边墙出现不稳定楔形块体滑落事件，该楔形体(图1)是由两个节理面、一个断层面共同切割，加上洞室开挖临空面形成一个不稳定四面体，结构面产状依次为：80°∠35°，250°∠60°，130°∠81°，楔形块体体积约8.15m3。断层处岩体较破碎，结构面由遇水软化的黏土矿物充填。根据现场反馈，开挖此段时岩体稳定，未有明显渗水现象，次日打完锚杆孔后，出现明显渗水现象，且水量较大，当开挖面推进约59m时，楔形块体发生滑塌。分析认为，地下水是导致楔形块体发生滑塌的主要原因之一。

图1 现场图片

2.2 极限平衡法计算

结构面的参数根据现场情况和《工程岩体分级标准》(GBT50218-2014)确定，计算时取节理面粘聚力为30kPa，内摩擦角为25°，断层面粘聚力为20kPa，内摩擦角为20°。计算过程如下：

①确定结构面的法向量

②主动力计算

A=W=(γV)·g=(0 0 -211.9)

③确定滑动方向

根据上文滑动方向判据可知楔形块体沿节理面2即满足：

因此，此楔形块体滑动方向为：

④计算阻滑力

N1=N3=0

τ=c+σtanφ=31.7kN/m2

J2=τacosθ=330.4kN

J1=J3=0

⑤计算稳定系数

根据现场施工反馈，巷道开挖至此段时围岩稳定，巷道顺利通过，之后发生明显渗水现象，且水量较大，当巷道往前推进59m时，此处发生围岩小面积滑落事件。由此可见，地下水的作用不可忽视。

假定断层面的水压为20kPa时，此时：

A=W+U=(-103.9568 87.2353 -233.3894)

楔形块体滑动方向为：

楔形体的稳定系数为:

当断层面的水压为30kPa时，此时：

A=W+U=(-155.9352 130.8529 -244.134)

楔形块体滑动方向为：

楔形体的稳定系数为:

此时，不稳定楔形体的安全系数小于1 ，块体将发生滑落。

如表2所示，随着地下水压力的增加，不稳定楔形体的稳定系数逐渐降低，围岩稳定性下降。

表2 不同水压力下楔形体的稳定系数

利用极限平衡法计算时假定结构面为平面，而实际上岩体中的节理都是随机分布的，同一组节理由于多种因素的影响，变动性较大，结构面也并不全部是平面，稍有不准确，就会使计算结果有较大的偏差；计算时假定洞室开挖的轴线方向始终保持不变，对于稍微复杂的大型工程来讲，显然是不能完全满足工程要求的。

2.3 离散元法计算

利用3DEC离散元软件，针对该滑落事件进行稳定性的模拟计算，建立模型尺寸为50m×30m×50m。另外，考虑断层破碎带，断层出露厚度为4m(沿巷道轴向)，在巷道右边墙断层破碎带处按产状130°∠81°、80°∠35°、250°∠60°切出一个四面楔形体，如图2所示。

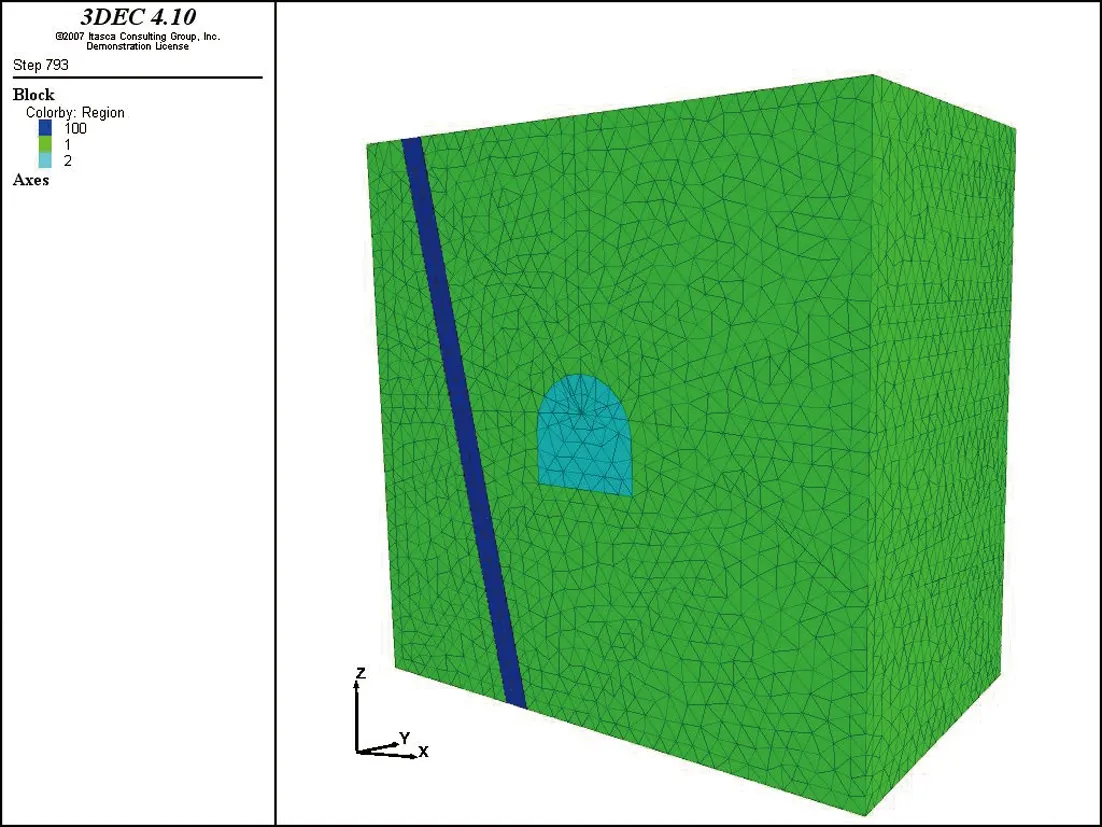
图2 洞室块体算例模型

模型假定岩块不产生渗流，地下水仅在裂隙中流动，初始地下水压力场按重力梯度设置。模型的左侧、右侧、前侧和后侧边界设为固定孔隙水压力，并且服从重力梯度。模型顶面和底面为定水头边界，其中顶面设定水压力为0.185MPa，底面设定水压力为0.685MPa。

根据勘察资料，该段交通巷道围岩质量等级Q值范围在1～10之间，断层破碎带Q值为0.04，故本次模拟围岩取1≤Q<4，断层处取0.01≤Q<0.1。岩体物理力学参数见表3。

表3 岩体物理力学参数

考虑渗流情况时，设定节理初始隙宽b0=1×10-4m，最大隙宽bmax=1×10-3m，残余隙宽br=1×10-5m。

2.3.1 应力场分布特征

如图3、图4所示，渗流情况下洞室周边最大主应力和最小主应力比无渗流情况下小，且渗流情况下洞室围岩局部产生0.185MPa的拉应力，围岩产生拉破坏。其主要原因是地下水渗流时，水的渗透压力和拖拽力加剧了裂隙的剪切和拉裂破坏，应力得到释放而导致。

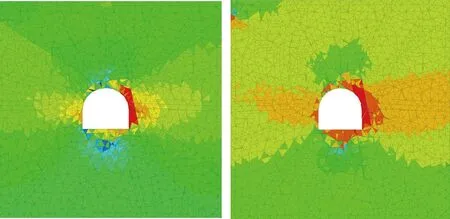
(a)无渗流情况(b)渗流情况

(a)无渗流情况(b)渗流情况

2.3.2 位移场分布特征

如图5所示，无渗流条件下楔形体区域的最大位移为37.6mm，渗流条件下的最大位移最大值为130.4mm，楔形体整体出现较大的变形。

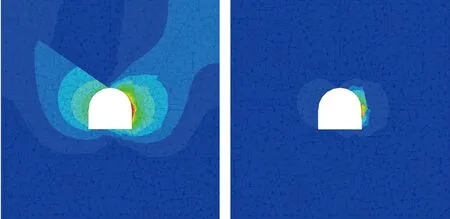
(a)无渗流情况(b)渗流情况

2.3.3 塑性区分布特征

如图6所示，由于存在断层，巷道周边的塑性区范围都较大，渗流条件下巷道周边塑性区的范围和厚度比无渗流情况下更大，塑性区体积增大约1000m3。其主要原因是由于岩体中的地下水使得围岩强度降低，进而导致围岩破坏的区域越大。

离散元法的优势在于其可以较好地实现块体间的分离、旋转及块体垮落等大位移运动的过程，又能计算岩块内部的变形与应力分布。同时，能够考虑初始地应力、围岩变形和非滑面抗剪性能对块体稳定性的影响，计算更符合实际情况。对大型地下工程，洞室开挖后，围岩会产生裂隙和发生大规模垮落，在这种条件下利用3DEC软件计算可使地下工程的模拟解更为合理。

(a)无渗流情况(b)渗流情况

3 结束语

本文利用极限平衡法和离散元法分别计算有无地下水渗流作用时地下洞室不稳定楔形体的稳定性，结果表明，地下水的存在会降低不稳定楔形体的稳定系数。通过对比分析，考虑地下水渗流作用下，楔形体及周边围岩的主应力比不考虑渗流情况下小，楔形体及周边围岩的位移量和塑性区面积比不考虑渗流情况下大，围岩的稳定性比无渗流情况下更差。