2005—2020年我国5级以上地震地理位置聚类分析*

陈嘉琳 尤添革,2 宁 静,2 许一涵 温芫姚 尤学敏

(1.福建农林大学计算机与信息学院，福建 福州 350002；2.福建省统计信息研究中心，福建 福州 350002;3.国网信通亿力科技有限责任公司,福建 福州 350001)

0 引言

根据全球板块分布图可知，我国地处欧亚板块的东南部，与太平洋板块相邻，受环太平洋地震带和欧亚地震带的影响，该地理位置决定了我国是个多地震的国家。据地震观测统计，我国大陆七级以上的地震占全球大陆七级以上地震的1/3，因地震死亡人数占全球的1/2。随着全球地震活动进入新一轮活跃期，21世纪地震地质灾害将成为最具威胁力的自然灾害之一，因此倍受人们的关注[1]。

分析地震的时间与空间分布特征是研究地震活动的一项基础工作，在已有历史数据的基础上，对未来地震发生的时间和区域的预测提供一定帮助。目前，国内有大量关于中国地区地震发生的时空分布特征研究，以指导地震的中短期预测工作。杨格格等[2]分别从时间和空间方面对新中国成立60年以来的陆域地震灾害进行了讨论；李鸣蝉等[3]使用K-means聚类、层次聚类、DBSCAN聚类等方法，从空间角度对云南2014年的地震丛集规律进行研究；刘洋等[4]使用聚类方法对大连地区3级以上的地震展开聚类分区的研究。地震在空间分布上存在着区域性，马禾青[5]等对中国大陆地震成组活动特征进行统计分析，表明1971年以来中国大陆5级以上地震的成组性较好，地震成组率和盲目预测准确率分别达43%和23%；蔡昕芮[6]对中国地震发生频数及区域性特征进行了统计分析。

关于地震发生的年份、月份、具体时刻等数据量较大，收集分析地震相关数据发现，各地震点的发震时间存在分布较散的特点；关于地震发生地点的经纬度数据较为抽象，已知经纬度的情况下无法直观了解中国地震的总体空间分布。本文将地震的经纬度转化为空间中的离散点，从而直观表示出中国各地区所发生的地震情况，并采用聚类方法对中国2005—2020年所发生的5级以上地震进行划分，发掘潜在的地震群，了解聚类所得到的簇其所处的地震带及地理结构，从而进行地震活动的分区调查与识别，提醒人们有意识地加以防范，减少地震所带来的经济损失和人员伤亡。

1 数据与方法

1.1 数据来源

地震的三要素为发震时刻、震级、震中，本文收集了中国2005—2020年5级以上地震数据作为样本数据。本文所有数据均来自国家标准统计数据，包括各年《中国大陆地震灾害损失述评》《国家统计局统计年鉴》。

对数据进行处理时，删除了地震中心位于中外交界处的地震数据，余下为有效数据，共493条。

1.2 统计方法

采用描述性统计方法，对中国2005—2020年(共16年)5级以上地震的总体分布情况进行研究。利用K-means聚类方法，将相近的发震地点聚为一类，旨在发现地震发生的区域性特点。K-means算法是采用划分的方法，其主要思想是将相似的点划分到同一簇中，不相似的点划分到不同的簇中，在K-means算法中可使用不同的距离来衡量点之间的相似性。

2 实验与分析

2.1 我国地震整体情况描述分析

资料表明，当地震级数≥4.5级、<6级的称为中强震(本文中强震主要分析≥5级、<6级的地震)，>6级、<7级的称为强震，>7级、<8级的称为大地震，8级及以上的称为巨大地震，本文统计分析中国发生中强震、强震、大地震、巨大地震4个等级地震情况，详见表1。

表1反映了2005—2020年中国5级以上地震的总体情况。可见，中国发生5级以上地震次数众多，按照地震级数呈现递减的趋势，震级为5～6级之间的地震最多。近年来，由于我国建筑抗震减灾性能不断加强，对不同建筑材料的抗震性进行改进，中强震造成的经济损失及房屋坍塌情况得到了较大改善。

表1 地震震级频率统计

根据震中位置的经度、纬度，利用Arcgis在地图中将2005—2020年中国5级以上地震以散点方式表示出来(图1)。

从图1可见，中国台湾地震分布十分密集，常常发生地震，据统计，2005—2020年台湾5级以上地震次数128次，地震级数大部分为5～6级之间；中国西部地域辽阔，地震分布较为分散，但地震频率较高，由北向南形成新疆—西藏—青海—四川—云南，其中，在中国西部与邻国交界处地震尤为频繁；中国东北部5级以上地震次数少，分布较为分散；在中国内陆东南地区5级以上地震发生频率极少。

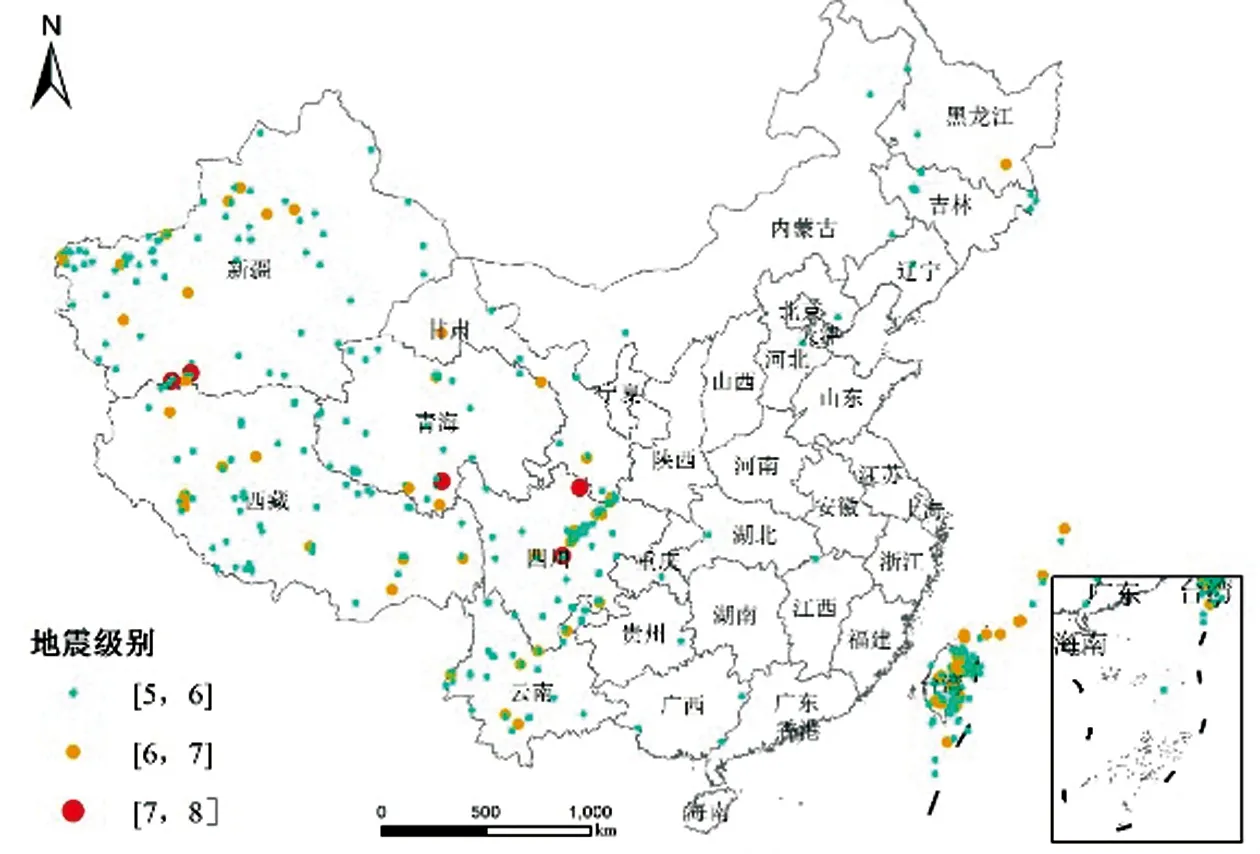
图1 中国2005—2020年5级以上地震的分布情况

2.2 我国地震发生时间分析

根据2005—2020年我国每年5级以上地震次数，绘制柱形图(图2)。可见，中国5级以上地震在2005—2020年没有呈现十分明显的规律性变化。其中，较为特殊的年份为2008年，次数为97次，呈现较为显著的活跃，地震次数次高的年份为2013年，在其余年份地震次数并没有大的波动。

从2008年5级以上地震发生地点来看，四川省发生5级以上地震次数为41次，占2008年中国5级以上总地震次数42.2%。四川省汶川县在2008年5月12日发生了8级的特大地震，造成了巨大的经济损失、房屋坍塌，以及较多的人员伤亡。据统计，四川省在当月共发生5级以上地震30次，除了汶川县外，还包括彭县、都江堰市、青川县、平武县等地。陈学忠[7]等利用Kolmogorov-Smirnov分布检验法，对龙门山断裂带的地震活动进行了检验，得出在2008年汶川特大地震前，地震的月频度标准差、偏度、峰度等值都发生了不同形态的短期异常变化，该变化与汶川地震的发生具有较大的关联性。

图2 2005—2020我国5级以上地震在每年的频数分布图

根据2005—2020年我国各月5级以上地震次数，绘制柱形图(图3)。从图3可以得到，1—3月次数发生较为稳定；5—8月地震发生次数较多，为一年中最频繁时期，而该时期我国正处于夏季；9—12月期间发生地震的次数逐步减少，10月为一年中最少的时期，该时期我国正处于冬季。从以上分析可得，我国5级以上地震发生的次数在夏季多于冬季，地震发生的原因与季节因素是否有紧密联系，需要进一步分析地区的地质等因素。

《死水微澜中》蔡大嫂对于自己的婚姻有着自己的主见，从第一次依照父母之命媒妁之言到第二次红衣教暴乱之后自己主动嫁给顾天成，她不顾父母的反对。女性婚恋观的改变是女性独立平等意识觉醒从的一个重要标志。蔡大嫂对于嫁给顾天成的想法很简单也很朴素，衣食无忧安身立命。她脱离了古代传统女子那种“女子丧夫不得改嫁”的传统模式。同时在于罗歪嘴产生婚外情时，并没有偷偷摸摸，而是堂而皇之，完全不避讳世人的目光。蔡大嫂在婚恋上所表现出来的那种非凡勇气是时代洪流下女性对抗封建枷锁的一把利剑。

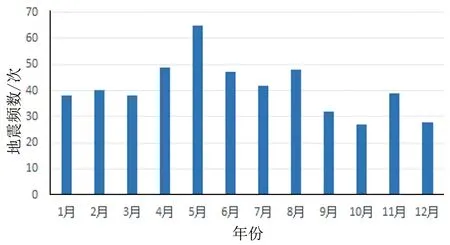
图3 2005—2020我国5级以上地震在各月份频数分布图

2.3 聚类算法及模型评估

2.3.1 K-Means聚类算法

利用K-Means聚类算法对全国各地区进行聚类，将全国划分为多个地震区。K-Means聚类算法是一种基于向量距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

K-Means算法的基础是最小误差平方和的准则，本文中K-Means算法具体流程如下：①从5级以上地震样本对象任意选择n个对象作为初始聚类中心；②根据步骤①设置的n个聚类中心，计算每个对象与这n个中心的距离；③经过步骤②的计算，把所有对象与离它最近的中心归在一个类中；④重新计算每个类的中心对象的位置；⑤重复步骤③和④，直到类中的归类几乎不发生变化为止。

本文采用欧几里得距离，各地震点到质心的距离公式为：

(1)

式(1)中，x表示簇中的一个样本点，u表示该簇中的质心，i表示组成点x的每个特征。

根据对中国整体地震分布的初步分析，选取初始聚类中心n=3和n=4，得到中国地震聚类的分布图，如图4、图5所示。

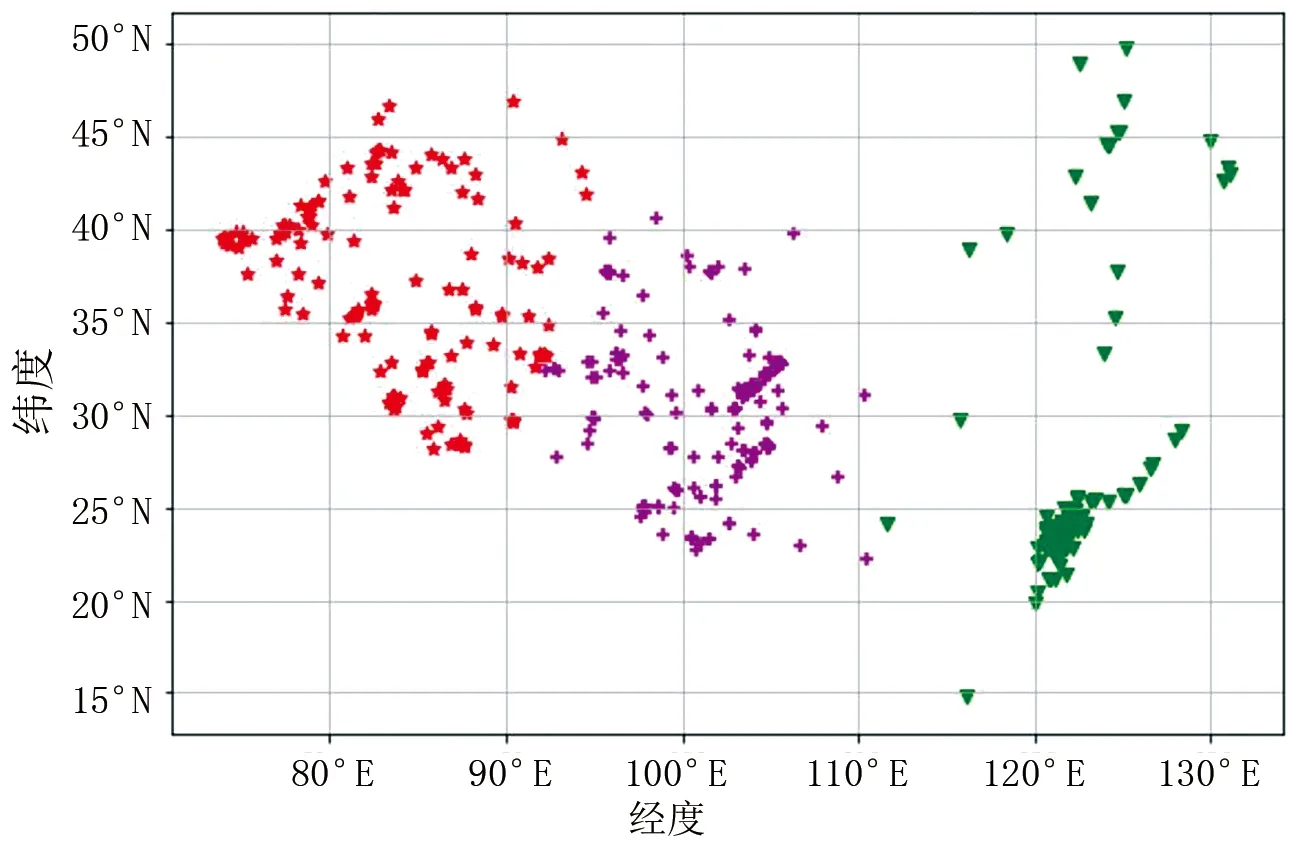
图4 选择3个初始对象作为聚类中心的地震分布图

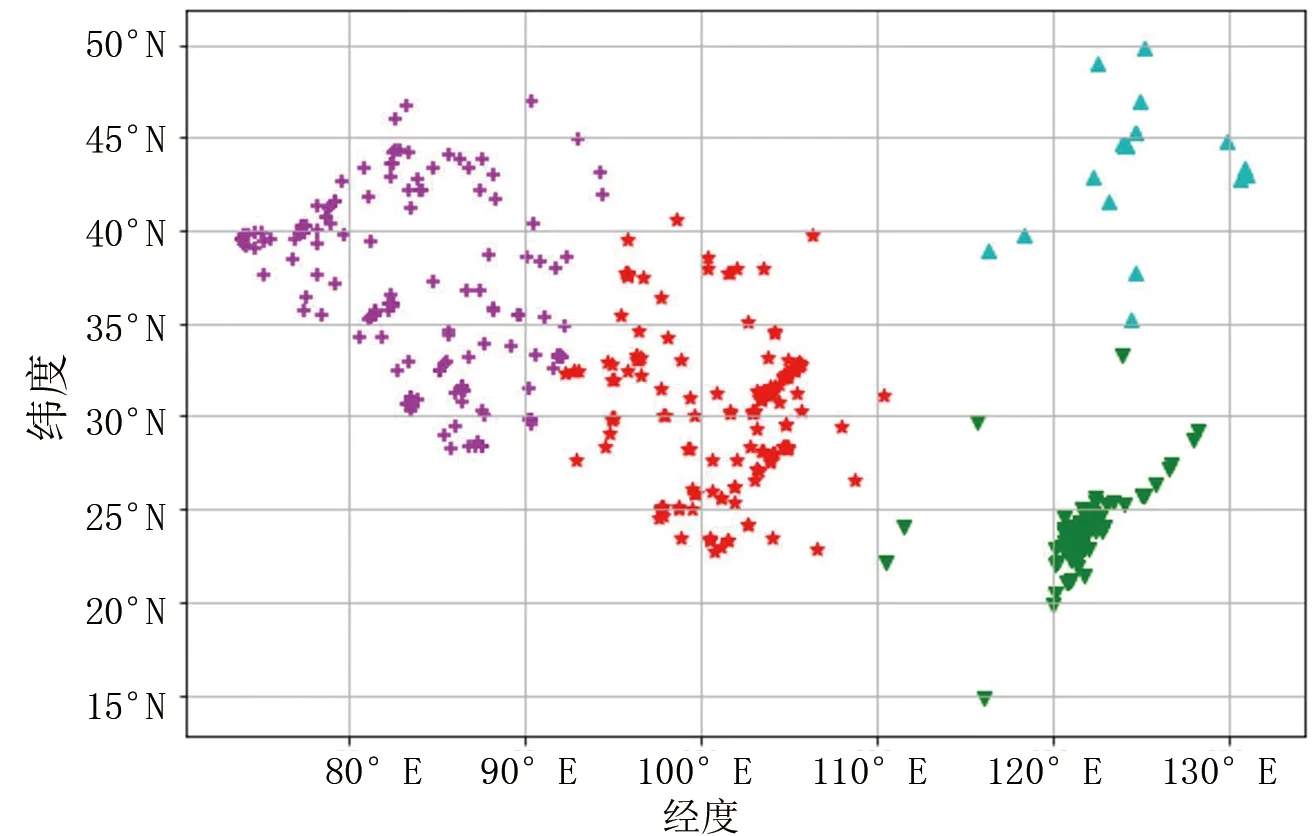
图5 选择4个初始对象作为聚类中心的地震分布图

对中国2005—2020年发生的5级以上地震进行聚类，当聚类类数k=3时，得到质心的经纬度分别为[26.44，122.18]，[36.86，83.69]，[30.53，101.44]；当聚类类数k=4时，得到的质心的经纬度分别为[36.86，83.69]，[23.89，121.72]，[30.58，101.39]，[43.52，124.71]。

2.3.2 簇内平方和Inertia

在K-means聚类算法中，其目标是确保“簇内差异小，簇外差异大”，由此得到中国5级以上地震主要分布区域，因此本文通过衡量类间差异来衡量聚类的效果。

Inertia是用距离来衡量类内差异的指标，又称为簇内平方和，数学公式为：

(2)

式(2)中，m为一个簇中样本的个数，j是每个样本的编号。

由Inertia的性质可知，Inertia的数值越小，代表每个类内样本越相似，聚类的效果越好，即该地区发生的地震可能具有相似性，处于同一地震带或者为同一地震区。当聚类簇数k=3时，Inertia的值为21448.2170；当聚类簇数k=4时，Inertia的值为14230.4403。聚类簇数k=4时的Inertia值明显低于k=3时的Inertia值，由Inertia的性质可知，分为4类的效果要明显比分为3类的效果好。

经过数据计算得知，随着聚类簇数k的增大，Inertia呈现下降，每一个点自成一类，其簇内平方和即是最小的，但这并不代表聚类的效果是最好的，因此还需要借助其他指标进行判断。

2.3.3 轮廓系数

轮廓系数是最常用的聚类算法的评价指标，它针对每个样本进行定义，其中，样本与自身簇中的其他样本的相似度为a，等于样本与同一簇中所有其他点之间的平均距离；样本与其他簇中的样本相似度为b，等于样本与下一个最近簇中所有点之间的距离。若b远大于a，则表明“簇内差异小，簇外差异大”，说明聚类效果较好。

单个样本的轮廓系数计算公式为式(3)、式(4)。

(3)

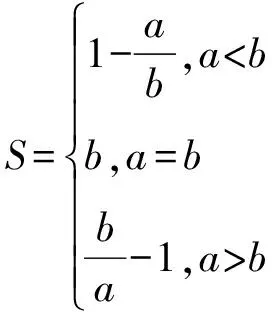
(4)

轮廓系数的范围为(-1，1)。其中,越接近1表示样本与自身簇中的样本很相似，并且与其他簇中的样本不相似；当样本点与簇外的样本更相似时，轮廓系数为负数；当轮廓系数为0时，则代表两个簇中的样本相似度一致，即两个簇应该合并为一个簇。

根据已经聚类的结果，求得当k=3时，轮廓系数为0.615；当k=4时，轮廓系数为0.653，轮廓系数更大，因此得出其聚类效果较好。

2.3.4 Calinski-Harabaz指数

对于有k个簇的聚类而言，Calinski-Harabaz指数S(k)公式为：

(5)

式(5)中，N为数据集中的样本量，k为簇的个数，Bk是组间离散矩阵，即不同簇之间的协方差矩阵，Wk是簇内离散矩阵，即一个簇内数据的协方差矩阵，tr表示矩阵的迹。

使用Calinski-Harabaz指数S(k)来衡量聚类效果时，值越高越好。根据已经聚类的结果，求得当k=3时，Calinski-Harabaz指数为1440.136；当k=4时，Calinski-Harabaz指数为1526.777，k=4时，Calinski-Harabaz指数更大，因此得出其聚类效果较好。

3 结论

本文利用2005—2020年中国发生5级以上地震的数据，从时间角度进行了简单的描述性统计分析；从空间上进行了聚类分析，得出下述结论：①地震聚类后的空间共分为4个区域，以中国东南部以及西部为代表，地震的次数较多、震级较大，空间分布密集；②2005—2020年，2008年呈现出峰值，地震是否呈现周期性，需要增加地震研究的时间跨度；③在K-means聚类中聚类评估效果较好。

本文采用可视化的方式对中国5级以上地震总体情况进行研究，直观地展现中国地震发生情况，有利于加强人们对近15年来地震总体情况的认知。从时间和空间的角度来看，地震的发生时段以及地震发生的区域的研究对人们防范地震有着重大意义。利用聚类分析可以发掘潜在的地震群，了解聚类所得到的结果所处的地震带及地理结构，从而进行地震活动的分区调查与识别，提醒各地区人们有意识地加以防范，减少地震所带来的经济损失和人员伤亡。由于本文对于时间的收集跨度仍不够大，对于地震周期的研究应收集更长时间跨度的数据进行时间序列分析。