单相感应电机无速度传感器矢量控制系统

马少才

(上海儒竞智控技术有限公司，上海 200438)

0 引 言

单相感应电机(SPIM)具有成本低廉、使用方便、结构简单、维修方便的优点，广泛应用于家电和小功率工业应用领域中，如电风扇、洗衣机、抽油烟机、家用水泵及小型风机等。单相电机一般直接接入电网，在这种情况下单相电机的能耗较高，如果不能进行调速会造成能量的大量损失[1-2],而且无法满足高精度驱动要求[3]；电机功率因数较低，会导致电网电能质量的降低[4]；电网电压和频率的波动会导致电机偏离其额定工作点，导致电流产生较大波动，随之导致电机转矩出现较大波动；此外，单相电机起动时，起动电流较大，会对电网造成较大的冲击电流[5]。

随着变频技术的发展，将变频技术应用于SPIM能解决其存在的上述问题。变频控制可以实现软起动，能够很好地解决SPIM直接起动对电网造成的冲击；矢量控制可改善SPIM椭圆形磁场，实现圆形磁场控制，实现转矩稳定；矢量控制可同时调节感应电机的励磁和转矩，可根据负载需求调整感应电机的电流，能够实现电机效率最优；矢量控制的调速精度高，调速性能优良；采用变频控制后单相电机不再会受到电网电压和频率波动的影响，极大提高了SPIM运行的稳定性；综上因素，矢量控制将极大改善SPIM的运行性能，降低SPIM不同工况下的损耗，对节能减排、实现双碳目标十分有意义。

SPIM增加速度传感器将大幅增加电机的成本，加大了安装难度，加大了电机的尺寸和体积，增加了相关的接线和接口电路，降低系统可靠性、可维护性[6]。因此采用无速度传感器控制成为电机调速系统的发展趋势，也有利于目前大量SPIM存量产品的升级改造工作。

在SPIM无位置变频控制方面：文献[1-7]均采用了基于模型参考自适应观测转速的转子磁链定向的矢量控制方案；文献[2]介绍了基于电流模型磁链观测的转子磁链定向矢量控制，介绍了基于定子电压模型计算定子磁链的直接转矩控制；文献[8]介绍了采用基于定子磁链定向的矢量控制；文献[9]介绍了基于定子磁链计算的转子磁链定向矢量控制系统；文献[10]介绍了基于扩展卡尔曼滤波器计算转速的转子磁场定向的矢量控制系统；文献[11-12]介绍了基于状态观测器计算转速的转子磁场定向的矢量控制系统；文献[13]介绍了直接转矩控制系统。

本文结合SPIM的数学模型，通过混合磁链观测器对转子磁链进行观测，并进一步计算出转子磁链和转速用于进行基于转子磁链定向的矢量控制，经过仿真验证控制系统的可行性和有效性。

1 SPIM数学模型

1.1 静止坐标系数学模型

相对于三相感应电机，SPIM只有两相垂直绕组，分别为主绕组和辅助绕组，这在控制过程中避免了Clarke变换；绝大多SPIM定子绕组是不对称的，使得其数学模型更为复杂。

SPIM在两相静止坐标系下的数学模型为[1,4]

(4)

φsm=Lsm·ism+Msrm·irm

(5)

φsa=Lsa·isa+Msra·ira

(6)

φrm=Lrm·irm+Msrm·ism

(7)

φra=Lra·ira+Msra·isa

(8)

Te=p(Msrm·ism·ira-Msra·isa·irm)

(9)

(10)

式中:下标m、a分别代表电机主绕组和辅助绕组；下标s、r分别代表电机的定子和转子；V、i、R分别代表电机电压、电流和电阻；L、M和φ分别代表电机电感、互感和磁链；p、Te、TL、ωr分别代表电机的极对数、电磁转矩、负载转矩和转子角速度；J和f代表转动惯量和摩擦系数。

在数学模型上为了降低SPIM的不对称性，将电机所有参数折算到定子主绕组的匝数，其中定义：

n=Nsm/Nsa≤1

(11)

Vsaref=Vsa·n

(12)

isaref=isa/n

(13)

φsaref=φsa·n

(14)

Lsaref=Lsa·n2

(15)

Rsaref=Rsa·n2

(16)

Msraref=Msra·n=Msrm=M

(17)

式中:Nsm、Nsa分别代表电机主绕组匝数和辅助绕组匝数；n表示主绕组和辅助绕组的匝数比；下标ref表示辅助绕组经过匝数折算后的变量。

经过匝数折算后，SPIM数学模型式(1)～式(8)变更为如下：

(21)

φsm=Lsm·ism+M·irm

(22)

φsaref=Lsaref·isaref+M·ira

(23)

φrm=Lr·irm+M·ism

(24)

φra=Lr·ira+M·isaref

(25)

Te=P·M(ism·ira-isaref·irm)

(26)

经过匝数折算后，忽略Lsm与Lsaref之间的小误差，可以近似的认为Lsm=Lsaref=Ls。并进一步定义SPIM漏磁系数如下：

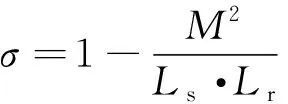
(27)

对式(22)、式(23)进一步进行推导，并将式(27)代入，可得：

(28)

(29)

至此，不对称单相电机数学模型经过一系列变换后其定转子磁链关系与传统三相感应电机保持一致，可视为对称磁链电机数学模型，为后续采用传统三相感应电机控制方法打下基础。

1.2 旋转坐标系数学模型

在旋转坐标系下，转子电压方程如下所示[4]：

(31)

其中τr为转子时间常数，其定义为

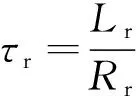
(32)

将矢量控制定向坐标轴固定在转子磁链上，则转子磁链在dq轴的分量可表达为

φrd=φr

(33)

φrq=0

(34)

(35)

将式(33)和式(34)代入式(30)，并化简可得：

(36)

将公式(33)、式(34)和式(35)代入式(31)，并化简可得在旋转坐标系下感应电机的转差角速度公式如下：

(37)

进一步可得感应电机的转速方程：

ωr=ωe-ωsl

(38)

式中:ωe为电机同步速。

1.3 定子电压数学模型

将不对称SPIM定子绕组电阻进行如下分解：

(40)

将式(39)和式(40)代入式(18)和式(19)，进行推导可得：

(42)

进一步定义：

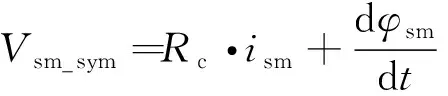
(43)

Vsm_sym=Rd·ism

(44)

(45)

Vsa_asy=-Rd·isaref

(46)

则定子电压方程可进一步表达为

Vsm=Vsm_sym+Vsm_sym

(47)

Vsa_ref=Vsa_sym+Vsa_asy

(48)

式中：下标sym代表对称分量；下标asy代表非对称分量。

当定子电压方程从静止向旋转坐标系进行变换时，只进行对称分量的转换。当从旋转坐标系向静止坐标系进行转换后，再进行非对称电压分量的补偿。由此SPIM在旋转坐标系下的对称参数模型定子电压方程可表达为

(50)

式(49)、式(50)与三相感应电机在旋转坐标系下的表达式一致。

2 转子磁链观测和速度估算

2.1 电压模型转子磁链观测

结合式(18)、式(19)、式(28)和式(29)可得到电压模型的转子磁链观测器表达式如下：

(52)

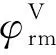
从式(51)、式(52)中可知转子磁链主要是对定子反电动势进行积分并转换得到，低速时，受定子电阻测量误差及电机在制造过程中定子线包参数差异影响，电压模型计算转子磁链计算结果会有误差；中高速时，定子电阻电压降较小，定子反电动势较高，电压磁链模型可以准确观测到转子磁链。

2.2 电流模型转子磁链观测

将电机定子两相电流经过同步旋转变换并按照转子磁场定向，得到dq坐标上的电流isd和isq，结合式(36)可以得到转子磁场定向下的转子磁场φr，再经过iPark变换到静止坐标系，就可以得到电流模型在静止坐标系下的转子磁链，其实现过程如下图1所示。

图1 电流型磁链观测器框图

2.3 混合模型转子磁链观测

从上述分析可见，电压模型与电流模型有各自的优缺点，将电流模型和电压模型进行级联，构建基于Gopinath型混合磁链观测器[14-16]，其具体结构如图2所示。

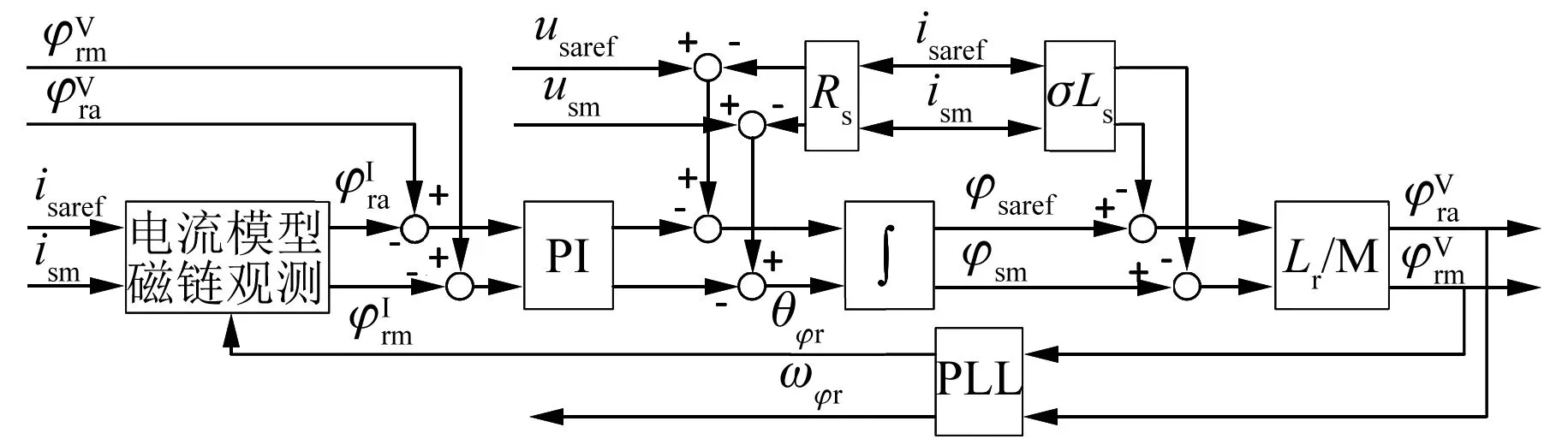
图2 电压电流混合模型的转子磁链观测结构框图

图2中，ωφr代表转子磁链角速度，其数值等于同步速ωe；θφr代表转子磁链角度。此闭环转子磁链观测器能实现在电流模型和电压模型之间自动平滑切换：低速时以电流模型结果为主；高速时以电压模型结果为主。低速到高速的过渡过程由图中PI控制器参数决定。其具体设计在文献[15-16]中有详细说明，此处不再赘述。PLL为锁相环，用于计算静止坐标系下转子磁链的速度和角度，PLL设计在文献[17]中有详细说明，此处不再赘述。

3 矢量控制仿真验证

为了验证新方法的有效性，利用软件MATLAB按照SPIM转子磁链定向建立了基于双闭环结构的电机矢量控制系统的仿真模型,逆变器为三相桥式逆变电路，该逆变电路产生和实现与传统三相空间矢量脉宽调制不同，对于单相电机产生方式在参考文献[18-19] 中均有详细介绍，此处不再赘述；观测器为前述混合模型转子磁链观测器；基于MATLAB的仿真框图如图3所示。

图3 SPIM转子磁场定向矢量控制系统仿真框图

仿真模型中PWM逆变器的载波频率为6 000 Hz，双闭环控制和磁链控制计算频率也均为6 000 Hz，仿真用SPIM参数为MATLAB默认参数，具体如下表1所示。

表1 SPIM参数

图4是基于转子磁链定向的非对称SPIM无传感器矢量控制转速突变时的仿真结果。负载为0.5 N·m，在8.5 s时，将转速由2 r/s提升为30 r/s；图4从上到下的波形依次为,转子磁链幅值误差、转子磁链角度误差、给定/实际转速和定子dq轴电流。

图4 SPIM转速突变仿真图

从图4中可以看到估算的磁链幅值与实际磁链幅值之间的误差极小，磁链角度误差在稳态条件下接近于零，动态过程会稍微大一些，说明该磁链计算方法的有效性；图4中实际转速与给定转速不重合的部分为转速调节过程。

图5是该系统在负载转矩突变时的仿真结果，在t=14.5 s时，将负载转矩由0.5 N·m提升为1.0 N·m。从上到下的波形依次为，转子磁链幅值误差、转子磁链角度误差、给定/实际转速、负载转矩和定子dq轴电流。

从图5中可以看到该算法具有较好的动静态控制性能，转子磁链幅值误差、相角误差、速度稳定误差和波动都非常小。更进一步说明了该磁链计算方法的有效性和可靠性，同时验证了仿真系统设计的合理性。

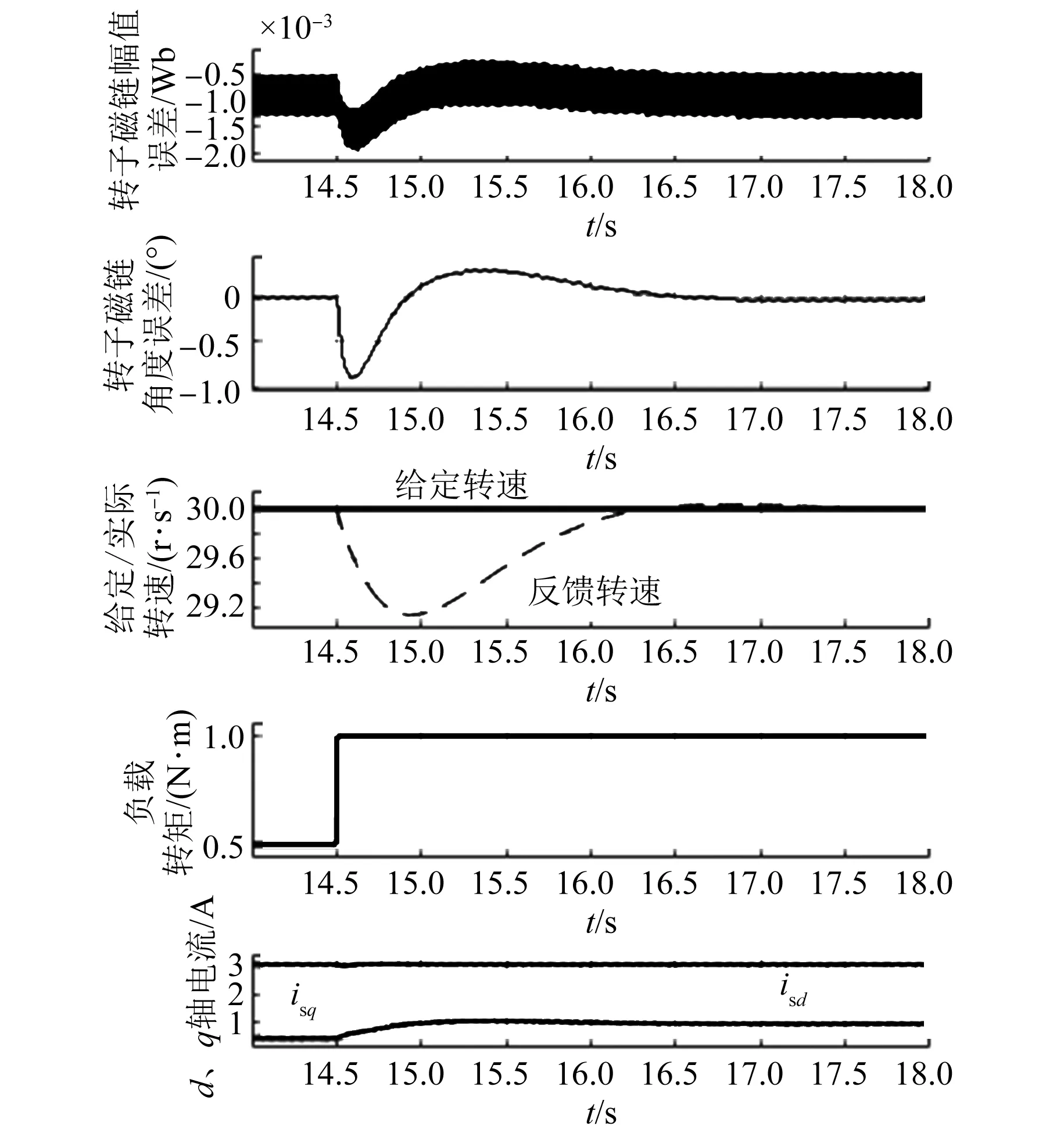
图5 SPIM负载转矩突变仿真图

4 结 语

本文从非对称SPIM的数学模型进行分析，对电机在不同坐标系的数学模型进行了推导，并针对电机的非对称性进行了对称化处理使单相非对称电机能够像三相感应电机一样进行矢量控制；采用混合模型转子磁链观测器进行了转子磁链观测；在上述内容基础上进行了非对称SPIM基于转子磁场的矢量控制研究，并建立了基于MATLAB的仿真模型，通过仿真验证了方案的正确性以及矢量控制在SPIM控制中的可行性和有效性。