感应电机模型预测转矩控制优化控制研究*

李耀华, 陈桂鑫, 王孝宇, 刘子焜, 刘东梅, 任 超

(长安大学 汽车学院,陕西 西安 710064)

0 引 言

感应电机模型预测转矩控制(MPTC)将逆变器所有开关状态遍历代入至预测模型，得到未来时刻的磁链和转矩预测值，以成本函数为评价指标，输出令成本函数最小的开关状态，近年来受到高度关注[1-6]。传统MPTC选择的电压矢量为固定采样周期，存在继续优化的空间。无差拍控制(DB)可通过预测模型精确计算得出使控制变量达到参考值所需的作用时间，实现电压矢量作用时间的最优化[7-10]。因此，将MPTC与DB结合，优化电压矢量作用时间，从而进一步减小磁链和转矩脉动就成为研究热点。根据MPTC与DB的先后执行顺序，可分为模型预测转矩无差拍控制(MPTC-DB)和转矩无差拍模型预测控制(DB-MPTC)[11-14]。

本文建立了感应电机MPTC系统、MPTC-DB系统和DB-MPTC系统仿真模型，对以上三种控制策略进行仿真对比。仿真结果表明：DB-MPTC系统控制性能最优。

1 感应电机MPTC

静止两相坐标系下，以定子磁链矢量ψs和定子电流矢量is为状态变量，定子电压矢量us为输入变量，三相感应电机数学模型如式(1)所示。

(1)

式中:Rs、Rr、Ls、Lr、Lm、p、ωm和ωr分别为定子电阻、转子电阻、定子电感、转子电感、定转子互感、极对数、电机机械角速度和电角速度。

感应电机转子磁链矢量ψr和电机转矩Te如下：

(3)

由一阶前向欧拉离散公式，将感应电机数学模型离散化可得感应电机下一时刻的定子磁链矢量和定子电流矢量预测模型如下：

ψs(k+1)=ψs(k)+Ts[us(k)-Rsis(k]

(4)

(5)

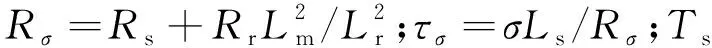
忽略逆变器导通压降，逆变器输出电压矢量即为定子电压矢量。

由此可得，下一时刻感应电机的转矩预测模型如下：

(6)

两电平三相逆变器可产生7个基本电压矢量，如下：

us∈{u0,u1,u2,u3,u4,u5,u6}

(7)

其中零电压矢量可由两个开关状态生成，具体选择以开关次数最小为原则[15]。

感应电机MPTC系统将逆变器电压矢量遍历代入至定子磁链、定子电流和转矩预测模型，可得到下一时刻的定子磁链和转矩，将预测得到的磁链和转矩代入至表征系统控制性能的成本函数，并将令成本函数最小的电压矢量作为输出。

定义表征磁链控制和转矩控制性能的成本函数如下：

(8)

感应电机MPTC系统如图1所示。

图1 感应电机MPTC系统

2 感应电机MPTC-DB

MPTC根据成本函数在7个基本电压矢量中选择最优电压矢量，但由于电压矢量作用时间均为固定采样时间，转矩脉动较大。因此，可采用DB进一步优化模型预测控制选择的电压矢量作用时间以减小转矩脉动。

将式(3)所示的转矩方程对时间求导可得：

(9)

将式(1)所示的定子电流矢量和定子磁链矢量状态变量代入至式(9) 以替换等号右侧的微分项，并采用一阶欧拉向前离散公式，对等号左侧转矩导数项进行离散化，则可得：

(10)

其中，

au含电压矢量变量，其作用时间为tu。在每个采样时刻，a0为常数项，作用时间为为Ts，则可得：

Te(k+1)-Te(k)=tuau+Tsa0

(11)

根据转矩无差拍原理，可得：

(12)

因此，实现转矩无差拍电压矢量理想作用时间tu为

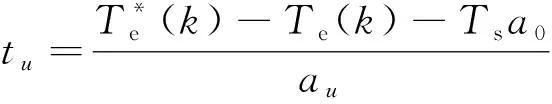
(13)

这里需要指出，模型预测控制选择的电压矢量并不一定能满足对磁链和转矩的增减定性控制，即模型预测控制选择的电压矢量对转矩的增减效果可能与无差拍期望值相反[16]。此时计算得到的理想作用时间tu<0。为减小转矩脉动，令tu=0。当转矩偏差较大时，计算得到的tu>Ts，说明电压矢量无法在一个采样周期内实现转矩无差拍控制，此时令tu=Ts。

经修正后，MPTC输出的电压矢量占空比不再固定为1，如下所示：

(14)

感应电机MPTC-DB系统如图2所示。

图2 感应电机MPTC-DB系统

3 感应电机DB-MPTC

上文提出的感应电机MPTC-DB实际分两步执行，第一步由MPTC选择出最优电压矢量，第二步根据转矩DB对第一步选出的电压矢量作用时间进行优化。但这种控制思想存在一定的逻辑问题，即第一步选择最优电压矢量是基于电压矢量作用时间为采样时间获得的，第二步对电压矢量作用时间的优化改变了第一级的前提条件，并不能保证为全局最优。为了解决这个逻辑问题，可先采用转矩DB计算得压矢量作用时间，得到修正的电压矢量，再根据模型预测控制选择最优的电压矢量，控制次序与MPTC-DB正好相反。

将电压矢量遍历代入式(13)，则可计算得到实现转矩无差拍的作用时间。如果tu<0，说明该电压矢量对转矩的增减效果与无差拍要求的控制方向相反，则不代入进行下一时刻的转矩和磁链预测，令其成本函数为极大值，予以舍弃。如果tu>Ts，说明该电压矢量无法在一个采样周期内实现转矩无差拍控制，此时令tu=Ts。对于零电压矢量，直接令其作用时间tu=Ts。因此，经过转矩无差拍控制环节后，电压矢量修正为

(15)

将修正后的电压矢量代入至磁链和转矩预测模型计算下一时刻的转矩和磁链，并通过式(8)所示的成本函数从中选择出最优电压矢量。为了简化预测计算，转矩预测模型如下：

Te(k+1)=Te(k)+tuau+Tsa0

(16)

感应电机DB-MPTC系统和程序流程图如图3和图4所示。

图3 感应电机DB-MPTC系统

图4 感应电机DB-MPTC流程图

4 仿真结果分析

基于MATLAB/Simulink分别建立三相感应电机MPTC、MPTC-DB和DB-MPTC仿真模型。仿真模型为离散模型，采样周期5×10-5s。参考转速初始为2 772 r/min，3 s时阶跃至-2 772 r/min，负载转矩为3 N·m，1.5 s时阶跃至-3 N·m，4.5 s时阶跃至3 N·m，仿真总时长6 s。为了防止电机起动电流过大，设置定子磁链幅值小于0.65 Wb时，电流大于6.5 A，输出零电压矢量，否则输出电压矢量u1，以实现电机软起动。通过试验搜索法确定MPTC成本函数的权重系数λ取值为17.5[17-18]。仿真用电机系统参数如表1所示。

感应电机MPTC系统仿真波形如图5所示。MPTC-DB系统仿真波形如图6所示。DB-MPTC系统仿真波形如图7所示。

表1 仿真用电机及系统参数

图5 感应电机MPTC波形

图6 感应电机MPTC-DB波形

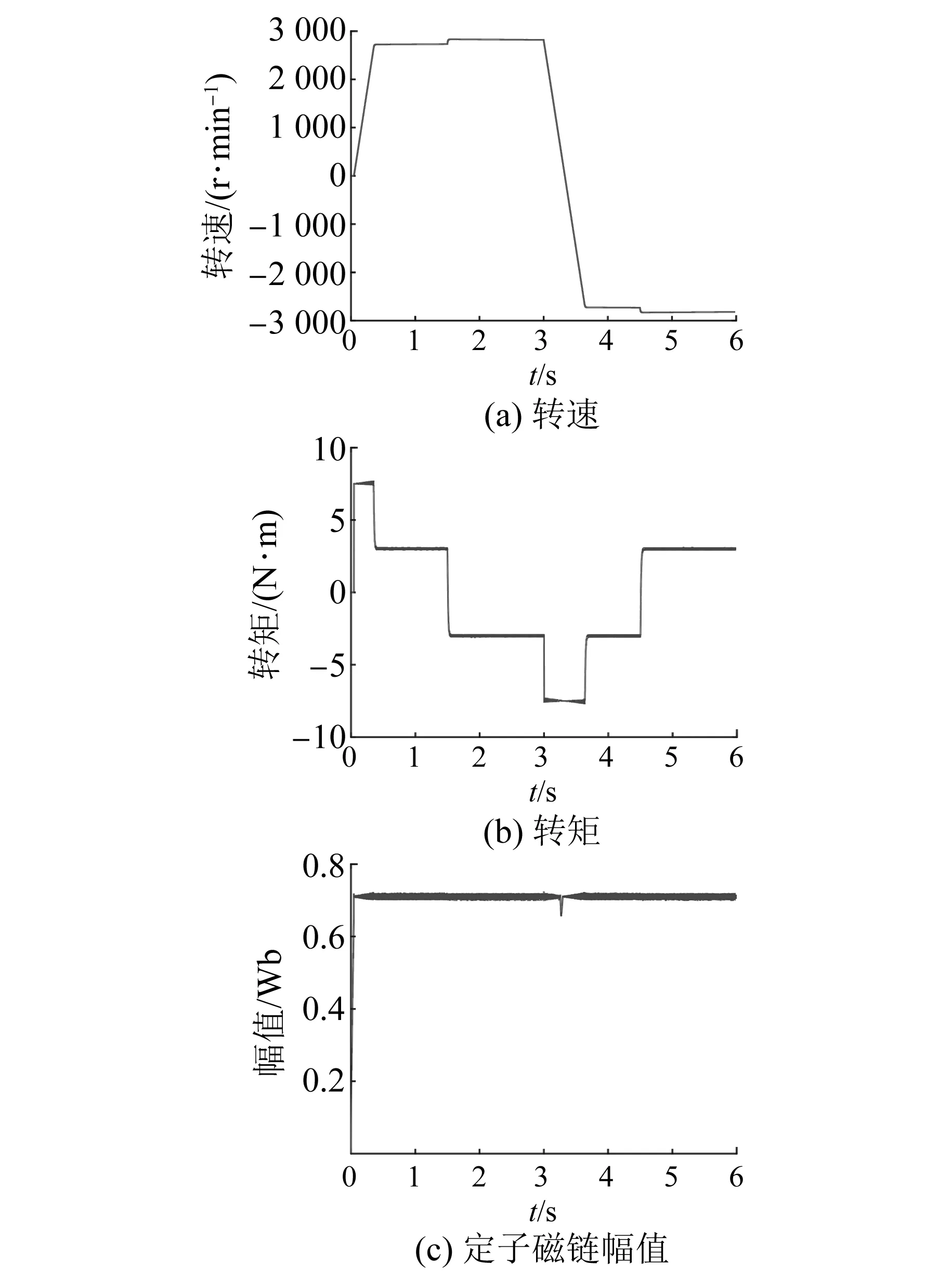
图7 感应电机DB-MPTC波形

定义转矩脉动均方根误差(RMSE)和磁链脉动RMSE分别如下

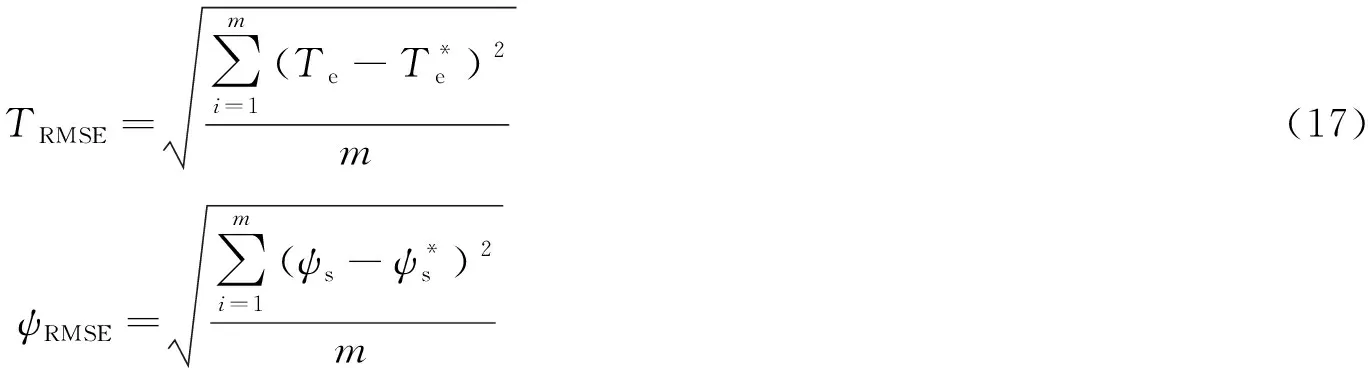
(18)

式中：m为采样个数。

0.05～6 s(不含电机软起动)三相感应电机MPTC、MPTC-DB和DB-MPTC的转矩脉动和磁链脉动RMSE如表2所示。

表2 三相感应电机MPTC、MPTC-DB和DB-MPTC控制性能

由仿真结果可知，与MPTC相比，MPTC-DB保持磁链脉动不变，转矩脉动RMSE减小26.92%。

与MPTC相比，DB-MPTC下转矩脉动RMSE减小75.83%，磁链脉动RMSE减小43.37%；与MPTC-DB相比，DB-MPTC下，转矩脉动RMSE减小66.93%，磁链脉动RMSE减小43.37%。

经统计，MPTC选择的电压矢量均无法实现转矩DB，MPTC-DB下，仅有44.04%的电压矢量可实现转矩DB，转矩无差拍模型预测控制下，99.80%的电压矢量可实现转矩DB。同时，DB-MPTC的第二级模型预测控制对磁链也进行优化。因此，这是DB-MPTC转矩脉动和磁链脉动得到进一步减小的原因。

5 结 语

基于感应电机MPTC系统、MPTC-DB系统和DB-MPTC系统仿真结果对比，得出结论如下：

(1) 感应电机MPTC、MPTC-DB和DB-MPTC均可实现四象限运行，电机运行良好。

(2) 感应电机MPTC选择的电压矢量作用时间固定，未能实现转矩无差拍。通过DB对电压矢量作用时间优化，部分情况可实现转矩无差拍，减小转矩脉动。但由于这种控制自身存在逻辑问题，并不是全局最优，对转矩脉动减小有限。

(3) 感应电机DB-MPTC在实现转矩DB的基础上，通过模型预测控制选择磁链和转矩控制效果最优的修正电压矢量，使绝大多数情况实现转矩无差拍，从而显著减小磁链和转矩脉动。