机械密封可靠性评估的神经网络和蒙特卡罗法★

冯嘉珍， 朱军华， 何宗科

（工业和信息化部电子第五研究所， 广东 广州 511370）

0 引言

机械密封是流体及动力机械系统中不可或缺的重要组成部分。 尤其在石油化工行业， 机械密封的可靠性对机械设备长期运行的稳定性与安全性有着深刻的影响。 因此， 对机械密封性能进行可靠性评估具有重要的工程实际意义。

张焕明[1]根据泵用机械密封的工作原理及结构形式， 定性地给出了影响泵运行可靠性的因素；陈启东等[2]结合Kolmogorov-Smirnov 检验理论判定某原油泵机械密封的寿命符合威布尔分布， 然后对机械密封的可靠度和寿命进行了评估； 丁思云等[3]基于专家经验法对机械密封发生失效的基本事件进行了定性分析； 吴勋等[4]针对无失效数据的情况， 利用多层Bayes 方法对涡轮泵端面密封可靠性进行了评估。 威布尔指数并非固定不变[5]， 这使得威布尔方法的使用范围受限。 专家经验法依赖于专家的个人主观经验， 使得可靠性评估结果的客观性较差。 Bayes 方法的准确性则受限于先验分布的选取。

针对上述研究的不足， 笔者引入应力-强度干涉理论， 结合机械密封性能寿命试验数据， 利用径向 基 函 数 神 经 网 络 （ RBFNN： Radical Basis Function Neural Networks） 来构建功能函数模型进行可靠性评估。

1 基础理论

1.1 应力-强度干涉理论

应力-强度干涉理论是机械结构可靠性评估的经典方法[6]。 假设X 表示基本随机变量， Y（X）表示强度， Z （X） 表示应力， Y（X）和Z（X）的概率密度函数分别为fY（Y）、 fZ（Z）。 将fY（Y） 和fZ（Z） 表示在同一坐标系中（如图1 所示）， 尽管强度Y （X） 的均值μ （Y） 大于应力Z （X） 的均值μ（Z）， 在干涉区域（图1 阴影所示的部分）仍有可能发生Y （X） 小于Z （X） 的情况（此时机械结构发生失效）。 机械结构处于可靠状态的概率可以表示为：

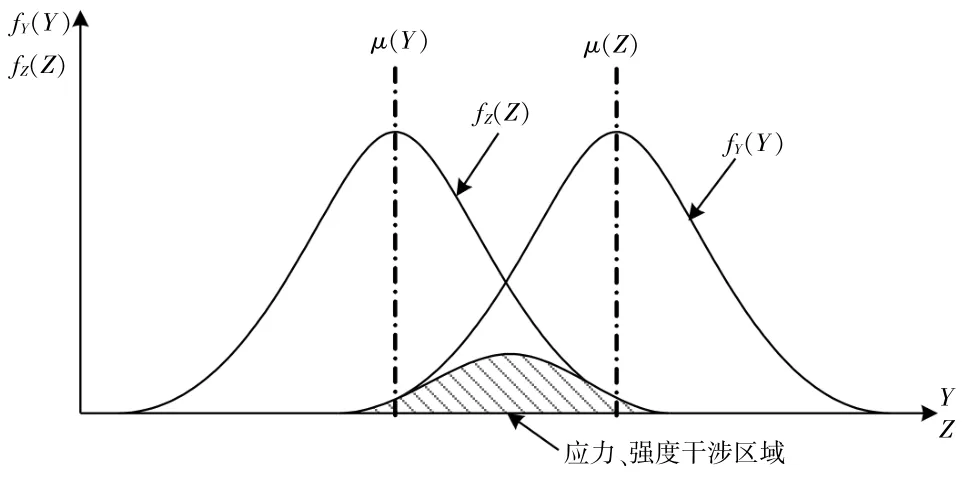
图1 应力-强度干涉模型

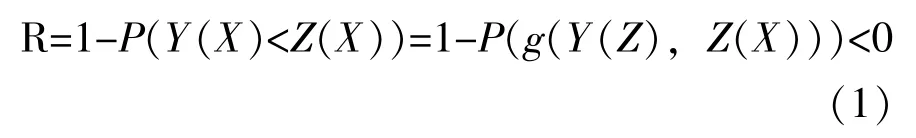
式（1） 中： R——可靠度。

g （·） 表示功能函数， 其表达式为：

1.2 RBFNN 模型

若功能函数g （·） 为隐式非线性， 将导致可靠性评估的困难。 通过构建g （·） 的高精度近似模型， 可以有效地解决这一问题。 RBFNN 为单隐层的3 层前馈网络， 能够以任意精度逼近任意的连续非线性函数[7]。 RBFNN 的第一层为输入层， 第二层为隐藏层， 第三层为输出层， 模型结构如图2所示。 RBFNN 中常用的径向基函数为高斯函数，表达式如下所示：

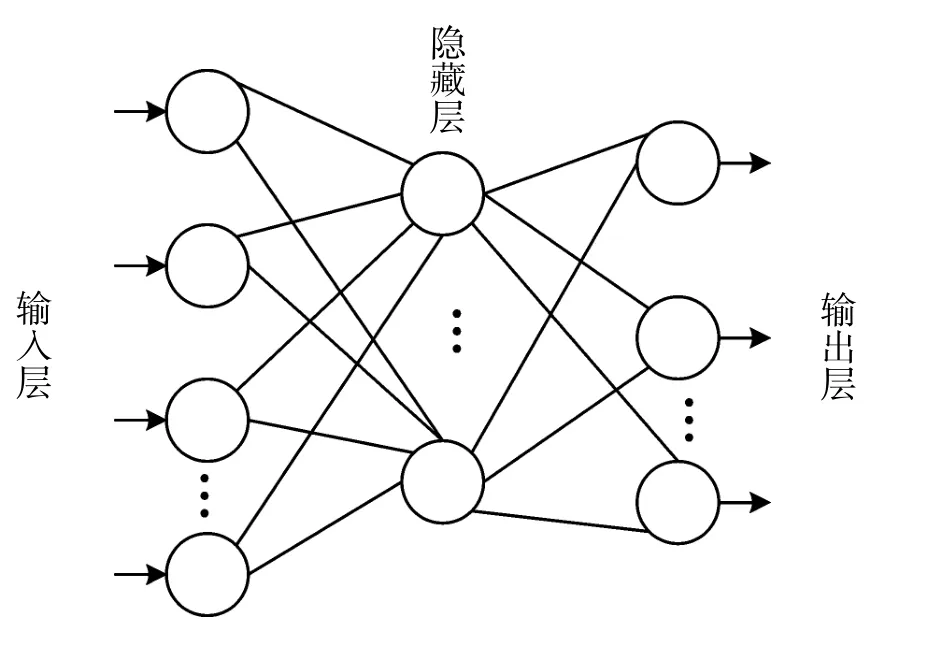
图2 RBFNN 结构图

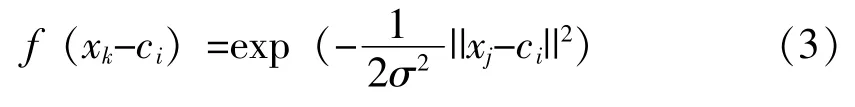
式

（3） 中： ||xk-ci||——欧式距离；

ci——高斯函数中心；

σ2——方差。

RBFNN 的输出可以表示为：

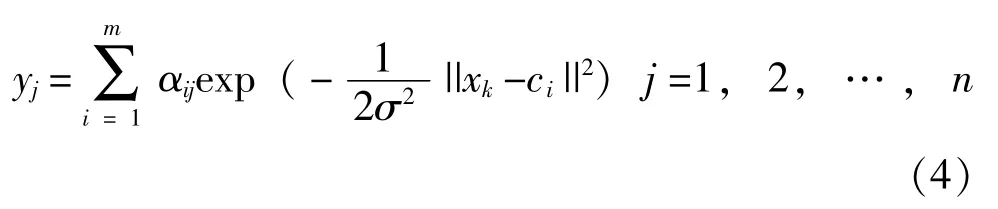
式（4） 中： xk——第k 个输入样本；

yj——第j 个输出结点的输出；

αij——隐含层到输出层的连接权值；

m——隐含层的节点数。

2 机械密封可靠性评估

2.1 机械密封可靠性模型

假设机械密封系统的泄漏量为q、 端面摩擦功耗为Nf。 磨损量q 随运行时间逐渐地增大， 超出规定阈值[q]时， 机械密封发生失效。 端面摩擦功耗Nf升高表征磨损率变大， 机械密封系统寿命缩短； 反之， 磨损率减小、 寿命延长， 但密封性变差。 可将泄漏量q 和端面摩擦功耗为Nf作为机械密封系统的性能参数。 q 和Nf决定于弹簧比压p1、介质压力p2和转速v[8]， 可将这3 个参数作为影响机械密封性能的敏感应力。 为评估机械密封系统的可靠性， 基于应力-强度干涉理论分别构建机械密封泄漏量q 的评估模型、 端面摩擦功耗Nf的评估模型， 如式（5） - （6） 所示。

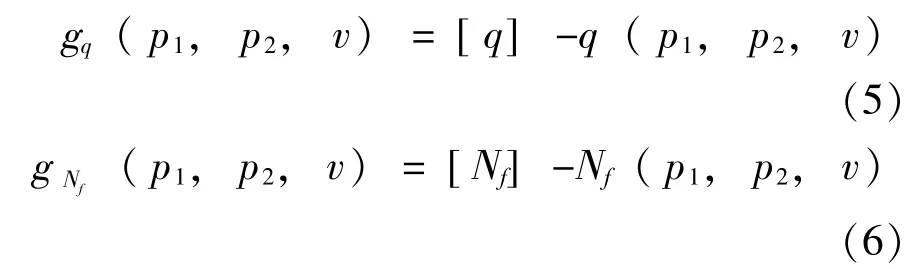
式（6） 中： [Nf]——许用端面摩擦功耗。

2.2 机械密封可靠性分析评估方法

泄漏量q、 端面摩擦功耗Nf与敏感应力p1、 p2和v 之间的函数关系为隐式， 无法直接进行可靠性评估。 利用RBFNN 分别构建gq（p1， p2， v） 和gNf（p1， p2， v） 的高精度近似模型g*q（p1， p2，v）、 g*Nf（p1， p2， v）， 然后结合蒙特卡罗（MC：Monte Carlo） 法进行可靠性评估。 所提方法的具体流程如图3 所示， 具体的步骤如下所述。

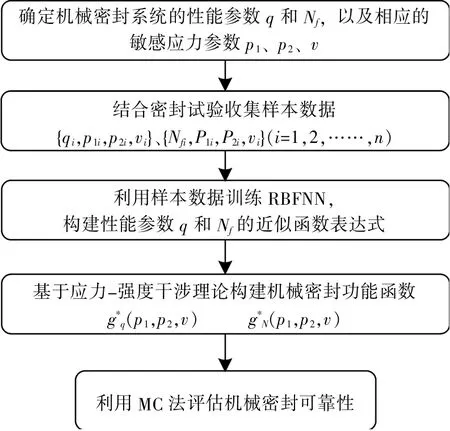
图3 基于RBFNN 与MC 的机械密封可靠性评估方法流程

1） 步骤1

确定与机械密封状态紧密相关的性能参数（包括泄漏量q 和端面摩擦功耗Nf）， 以及影响这些性能参数的敏感应力参数集（包括弹簧比压p1、 介质压力p2和转速v）。

2） 步骤2

结合密封性能试验， 收集性能与敏感应力参数集{qi， p1i， p2i， vi}、 {Nfi， P1i， P2i， vi}， i=2， 3，…， n， 构成训练RBFNN 的样本集。

3） 步骤3

分别利用样本集{qi， p1i， p2i， vi}、 {Nfi， P1i，P2i， vi} （ i=2， 3， …， n） 训练所构建的RBFNN，得到泄漏量q、 端面摩擦功耗Nf与敏感应力p1、 p2和v 之间近似函数表达式q*（p1， p2， v）、 N*f（p1，p2， v）。

4） 步骤4

结合机械密封的失效机理与应用要求， 确定机械密封性能对应的失效判据与失效阈值， 利用应力-强度干涉理论构建机械密封功能函数的近似表达式： g*q（p1， p2， v） = [q]-q*（p1， p2， v）、 g*Nf（p1， p2， v） = [Nf]-N*f（p1， p2， v）。

5） 步骤5

在功能函数gq*（p1， p2， v） 和g*Nf（p1， p2， v） 的基础上， 利用MC 法分析评估机械密封的可靠度。

3 案例分析

以GY70 型机械密封系统为对象， 泄漏量与端面摩擦功耗试验数据如表1-2 所示[9]。 利用RBFNN 分别构建泄漏量与端面摩擦功耗的近似模型。 假设泄漏量阈值[q]=3.9 mL/h、 端面摩擦功耗阈值Nf0=0.7 kW， 根据应力-强度干涉理论，GY70 型机械密封系统的功能函数可以表示为：

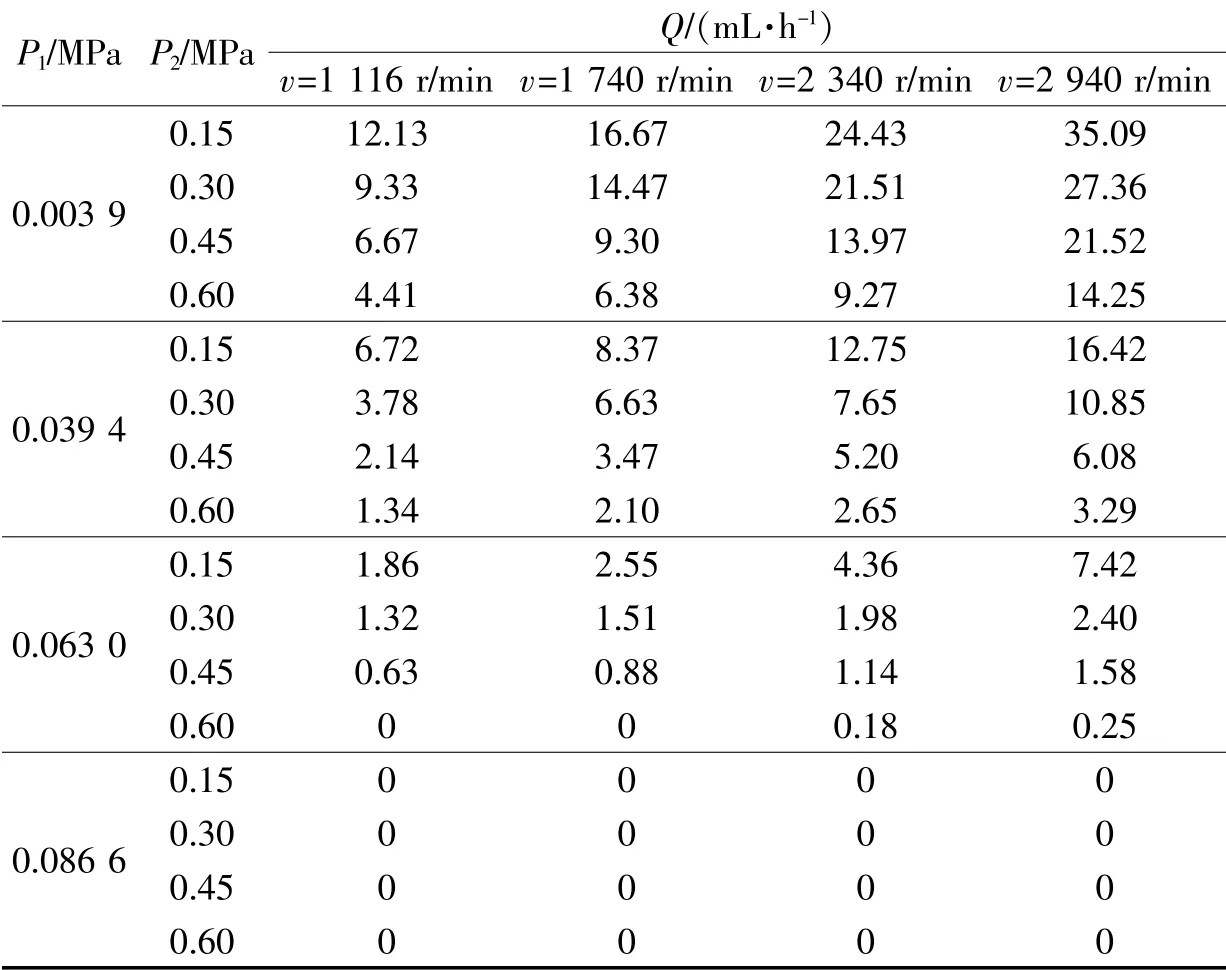
表1 泄漏量试验数据

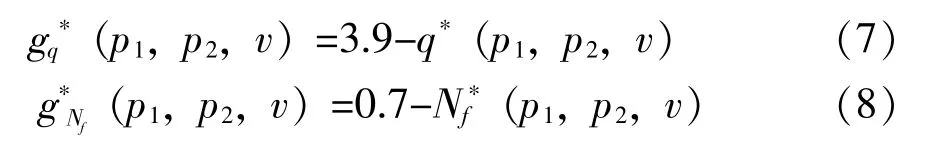
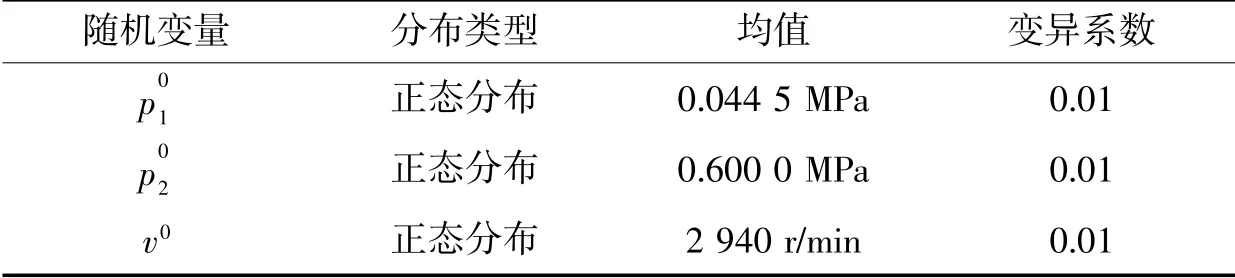
表3 GY70 敏感应力参数概率分布

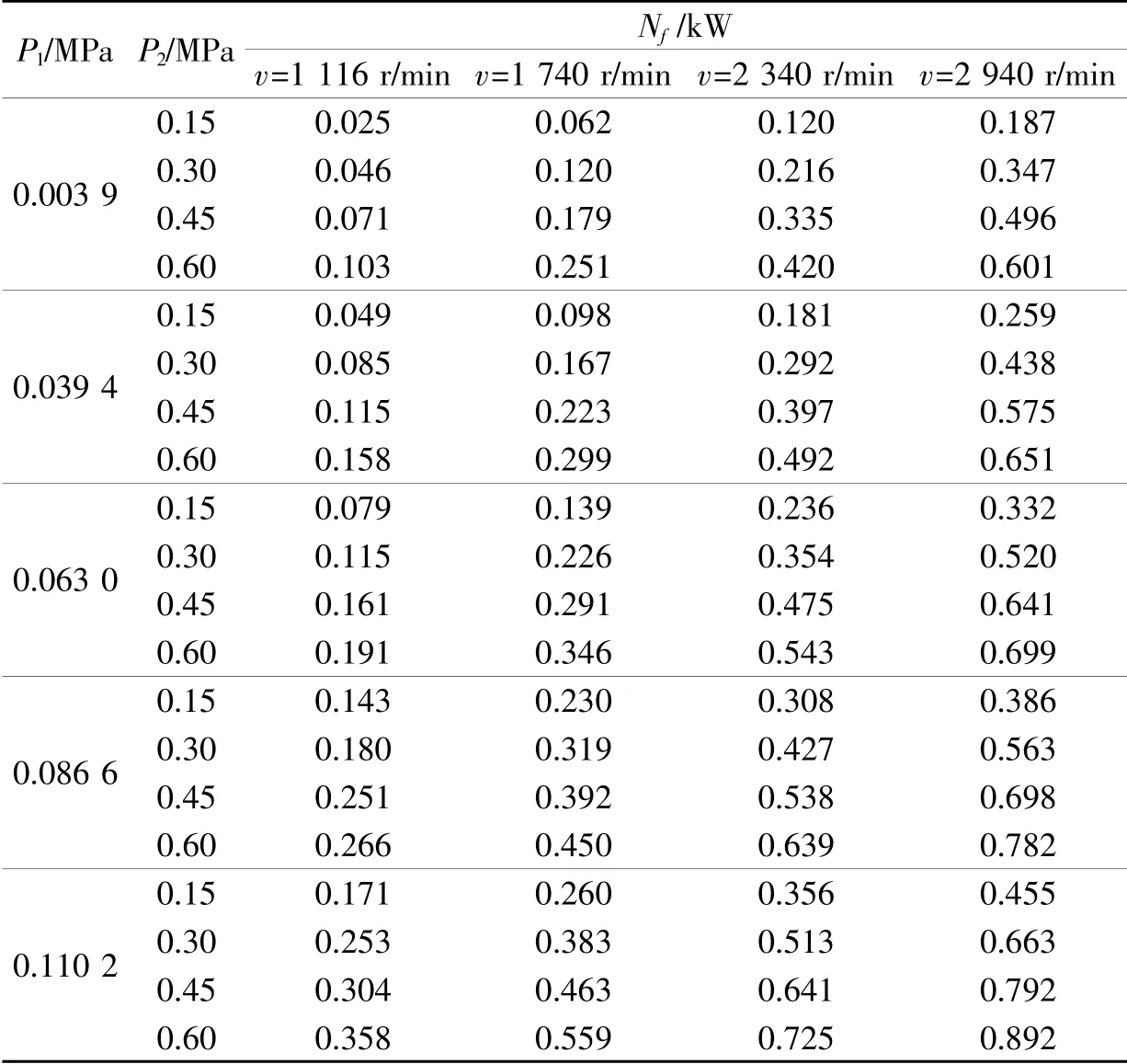
表2 端面摩擦功耗试验数据

4 结束语

针对机械密封可靠性评估， 提出了基于RBFNN 与MC 的方法，给出了方法的详细流程。 所提的方法有效地解决了机械密封可靠性模型为隐式非线性的问题， 具有一定的工程实用价值。