基于ABSUM的MIMO雷达频谱兼容波形设计

姚 誉 李泽清 范 文 杜晓林 吴乐南

①(华东交通大学信息工程学院 南昌 330031)

②(中国电子科技集团公司第五十四研究所 石家庄 050081)

③(烟台大学计算机与控制工程学院 烟台 264000)

④(东南大学信息科学与工程学院 南京 210096)

1 引言

相较于传统的相控阵雷达，多输入多输出(Multi-Input Multi-Output，MIMO)雷达能够发射多种波形信号，这些信号可能相互关联或不相关。得益于波形的多样性，MIMO雷达的目标检测能力、抗干扰能力、目标识别和分类能力得到了显著增强，发射波束设计的灵活性也得到了很大的提升[1，2]。雷达与通信系统在频谱拥挤环境下的共存问题是近年来学者关注的一个重要问题。当两种系统占用相同的频段时，就需要这种兼容性。例如，在宽带传输中，雷达系统占用很大的带宽，因此可能会与周边无线通信网络的频谱发生重叠[3]。目前关于频谱共存问题的研究大多数是从雷达角度出发，通过对发射波形设计的优化来实现频谱共存。

在MIMO雷达系统的收发联合设计中，可以考虑不同的约束条件来设计和优化发射波形[4—9]。例如，通过施加恒模(Constant Modulus，CM)约束或者峰均功率比(Peak-to-Average Ratio，PAR)约束使得雷达发射机能在饱和工作状态将性能发挥到最大，通过施加相似性约束来确保优化后的发射波形具有良好特性，通过施加频谱约束控制发射波形的频谱能量来实现频谱共存。存在信号相关干扰时，为了检测扩展目标，在发射波形的能量约束下进行收发联合设计，以最大化信干噪比(Signal to Interference pulse Noise Ratio，SINR)[10]。Cui等人[11]将雷达波形优化问题转化为纯相位约束问题，提出了坐标下降(Block Coordinate Descent，BCD)的迭代算法。Liang等人[12]设计了保持方向图形状的相位阵列优化方案，提出了基于交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)的相位恢复算法。Palomar团队[13]考虑了PAR约束下的恒模波形设计问题，提出了优化最小(Majorization-Minimization，MM)算法用以设计雷达发射编码。文献[14]针对信号相关杂波环境下的运动目标检测问题，研究了一种稳健的慢时间发射波形和接收滤波器联合设计方法，并利用Dinkelbach 程序进行求解。

针对雷达和通信系统频谱共存问题，De Maio和Abury等人[15]以输出SINR最大化为准则，研究了在能量约束和相似性约束下的雷达频谱兼容波形设计方法，并利用半正定规划与秩一分解(Rankone decomposition)理论对雷达发射序列进行优化。虽然基于半正定规划的秩一分解技术能够获得好的近似解，但求解半正定规划问题的计算复杂度较高，不太利于工程的实现。在此基础上，Wu等人[16]考虑频谱约束条件，提出了在MM算法框架下的改进(Successive Convex Approximation，SCA)算法，降低了每次迭代的计算复杂度。Tang等人[17]提出了一种基于ADMM的快速算法，数值结果证明该算法在计算时间上优于半正定规划算法，所设计的波形也能折中SINR、频谱共存和自相关函数的特性。随后，Fan等人[18]考虑了宽频带MIMO雷达在频谱密集环境下的发射波束合成问题，提出了一种改进的ADMM (Majorization-ADMM，M-ADMM)算法，通过利用一个光滑的凸函数对原始非光滑的非凸目标函数进行近似，然后利用ADMM算法的更新规则并行求解约束优化问题，最终降低了求解的计算时间。

针对频谱约束条件下MIMO雷达系统的联合收发设计问题，已有的方法包括顺序优化算法(Sequential Optimization Algorithm，SOA)[19]、逐次二次约束二次规划(Quadratically Constrained Quadratic Programming，QCQP)求解法[20]、BCD法[11，21]和MM求解法[13，22]。在文献[23]中考虑了PAR和相似度约束，并利用乘子块逐次上界最小化法求解了文献[19—22]中的优化问题。为保证与授权辐射器的频谱兼容性，在频谱、相似性和能量约束下的联合设计问题也通过文献[19]中的MM方法进行求解。在文献[24]中，作者利用半定松弛(Semie-Definite Relaxation，SDR)方法[25]将上述方法扩展到包括频谱、相似性和能量约束的问题中。然而，对于多约束优化问题[20]，文献[24]中的可行集并不能总是得到保证。在文献[26]中，通过在相似度和通信速率约束下联合设计MIMO雷达收发器的空时协方差矩阵，确保MIMO雷达和MIMO通信系统的共存。文献[27]设计了发射信号和接收滤波器组的迭代优化程序。它单调地改善了最坏情况的SINR，并收敛到一个平稳点。该方法还能够通过根据规定的时间或复杂度要求适当地选择迭代次数权衡SINR性能和算法复杂度。

ADMM算法通过将原问题分解为更小的子问题进行求解，更好地适用于大规模的约束凸问题。然而，对于一般的非凸问题，ADMM的收敛性分析仍然是一个开放性问题。迭代分块连续上界最小化方法(Block Successive Upper-bound minimization Method，BSUM)[28—32]通过引入原始目标的上界函数，可以将求解的非凸问题转换为依次优化凸函数问题。本文以输出SINR最大化为准则，构建了频谱约束和相似性约束条件下的发射波形与接收滤波器的联合设计问题，结合ADMM和BSUM算法的优点，设计了BSUM算法的变体(Alternating BSUM，ABSUM)算法，提出了一个原始对偶框架，该算法可以收敛到一个静态稳定点，使算法能够有效地解决约束非凸问题，数值仿真实验证明了该算法能够在合理的计算时间内取得更好的SINR，得到更优的目标检测性能。

符号说明：(·)T，(·)H，(·)*，||·||，|·|和E{·}分别表示转置、共轭转置、共轭、范数、取绝对值和统计期望值；IN×N表示N×N的单位矩阵；CN×1为 包含N×1向 量的复数集合；CN×N为包含N ×N矩阵的复数集合；⊗表示Kronerker积；diag{·}表示矩阵的对角元素；v ec{·}表示将矩阵按列排列形成列向量；ℜ{·}和ℑ{·}分别表示取实部和取虚部操作。

2 信号模型

其中，c=vec(C)，α0和αk分别表示目标和第k个干扰源的幅值。向量n既包括内部热噪声，也包括未知的、未经许可的、可能是敌对干扰器造成的干扰信号，以及与目标雷达共存相同频率的授权电信网络。此外，向量n被建模为一个复的、零均值的、圆对称的高斯随机向量，协方差矩阵和θk分 别为目标和第k个干扰源的角度，且θk θ0。H(θ)为 均匀线性阵列天线的转向矩阵，。以输出SINR作为性能指标，联合优化发射波形与接收滤波器来最大化输出SINR。在实际场景中，可能无法获得目标角度和干扰的准确信息，因此，可以合理地假设θ0和θk是不相关的均匀分布随机变量，分别具有已知的平均值和，即

基于SINR最大化的优化准则，在能量、相似性和频谱兼容约束条件下，雷达发射波形和接收滤波器联合设计问题可以表述为

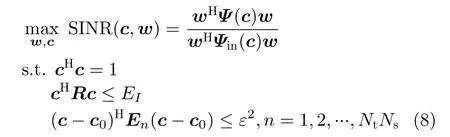
从式(8)可以明显看出，此问题为非凸问题，其包含非凸目标函数、非凸二次等式约束和非齐次二次不等式约束，是NP-hard问题[34]，很难直接求得上述问题的全局最优解。因此，需要设计一种新的迭代优化算法来求解问题(8)。

3 波形设计算法

ADMM算法可以将原来复杂的问题分解成为更小的子问题进行求解，更好地适用于大规模的约束问题。也被广泛应用于求解雷达波形设计问题[35—37]。针对凸问题，ADMM算法能够保证收敛到全局最优解，然而针对非凸问题，其收敛性仍是一个开放性问题。结合ADMM算法和BSUM算法的特点，本文提出一种新的优化方法，称其为ABSUM算法，该算法可以收敛到一个静态稳定点。其主要思想是在ADMM算法框架下，使用BSUM算法引入目标函数的上界函数，然后应用ADMM框架更新规则求解约束优化问题。所提出ABSUM算法兼顾了ADMM算法和BSUM算法的优点，具有更好的收敛性。首先将式(8)中的问题改写为实值形式：

因为在问题(9)中包括非凸目标函数和二次等式约束，其为一个非凸问题，直接求解比较困难。通过引入辅助变量可以把问题(9)中的非凸目标函数转换为关于每个变量的双拟凸函数。此外，问题(9)中的非凸二次等式约束可以修改为双仿射等式约束，即cr和tr的联合仿射。换句话说，对于固定tr，它在cr上是拟凸的，对于固定cr，它在tr上是拟凸的。因为目标函数是关于ck的拟凸函数，拟凸函数的上镜图也是凸函数，因此可以通过最小化的 上界函数来求解ck，同理也可求解tk。因此，利用ADMM算法可以求解问题(10)。在ADMM框架下，将等式约束置于原函数的增广拉格朗日函数中，而不是始终保持等式约束。更确切地说，问题(10)中的增广拉格朗日量为

3.1 接收滤波器优化

当ck和tk固定时，接收滤波器向量w的优化问题可以写为

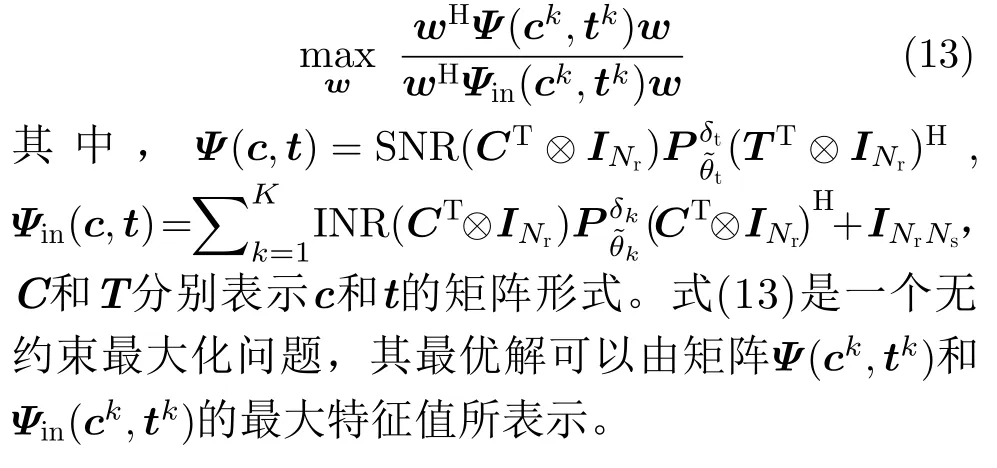
3.2 发射编码优化

为了处理具有非凸二次等式约束和二次不等式约束的问题，引入一个辅助变量进行问题修正。因此，对于每个原始变量，非凸目标函数可以转换为双拟凸函数。更重要的是，将非凸二次等式约束转化为双仿射等式约束。随后，利用块逐次上界最小化法和乘法器交替方向法，设计一种原对偶算法来求解改进后的问题。在该框架下，首先通过ADMM算法消除等式约束，然后通过最小化增广拉格朗日函数的上界函数来更新原变量。由于原始变量的每次更新都涉及一个二次规划问题，该问题的最优解可以用内点法求得。内点法的特点是将构造的无约束目标函数定义在可行域内，并在可行域求解极值点，即求解时探索点始终保持在可行域内。这样，在求解优化问题的过程中，所求得的解总是可行解，从而在可行域内部逐步逼近原约束优化问题的最优解。最后，根据上述步骤，总结了本文提出的ABSUM算法。

4 数值仿真与分析

本节提供了几组数值模拟实验来评估所提算法的性能。在理想情况下，即目标和干扰的角度是已知的情况，设计具有频谱约束和相似性约束的波形。假设MIMO雷达系统的发射天线数Nt=4，接收天线数Nr=8，每个脉冲的采样数Ns=64。线性调频(Linear Frequency Modulation，LFM)波形在脉冲压缩和模糊度方面有很好的特性，它是区分点目标和成像的好候选者。此外，具有正交发射波形的MIMO雷达在目标检测性能、角度测量能力和动态范围特性等方面优于传统雷达。参考波形c0选取正交LFM信号，其形式为[33]

4.1 收敛性分析

由于QCQP[20]，MM[22]，BCD[21]和SQR方法[8]不能解决本文所考虑的问题，因此，在接下来的分析中，我们将所提出的ABSUM算法与GFA[27]和SOA方法[19]进行比较，首先对3种优化波形的SINR迭代曲线进行比较，相比于GFA和SOA算法，ABSUM算法利用拉格朗日乘子将原问题分解成多个可求解的子问题，然后进行交替更新求解，使得优化问题能够获得更好的解。设频谱约束值为EI=10-4时，图2描绘了不同相似性参数下输出SINR值与迭代次数的关系。从图中可以看出ABSUM，GFA和SOA算法的SINR值都随相似性约束的增加而增加，通过增加相似度，即增加可用的自由度，可以实现更好的有用能量分布。此外，在ε′=0.5，1.0，1.3时，ABSUM算法均显著优于GFA和SOA算法，具体而言，相似性约束值为ε′=1.0时，所提出的算法与对比算法的增益约为2.3 dB和3.1 dB。

图1 已优化波形特征Fig.1 The feature of the optimized waveforms

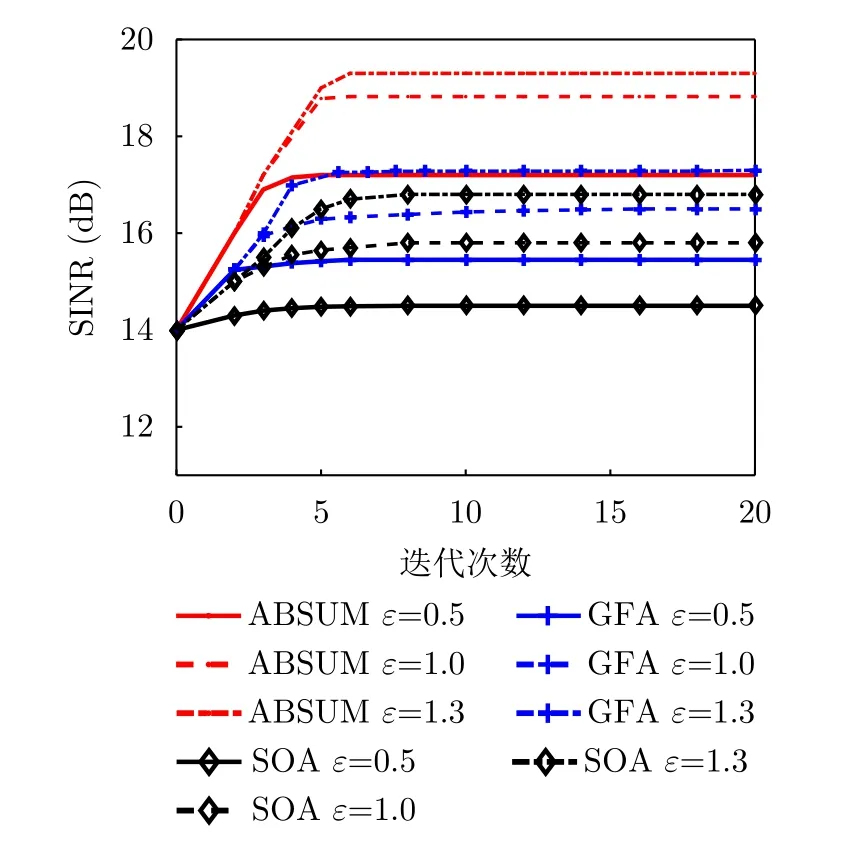
图2 频谱兼容和相似性约束下SINR的迭代曲线Fig.2 The SINRs with spectrum constraint and similarity constraint

表1 仿真参数Tab.1 Simulation parameter

假设频谱约束值为EI=10-4，表2 分析了ABSUM，GFA和SOA算法在不同相似性约束条件下的SINR性能。结果表明，ABSUM算法在SINR值方面优于GFA和SOA算法。此外，ABSUM算法的全局计算时间明显小于GFA和SOA算法的全局计算时间。

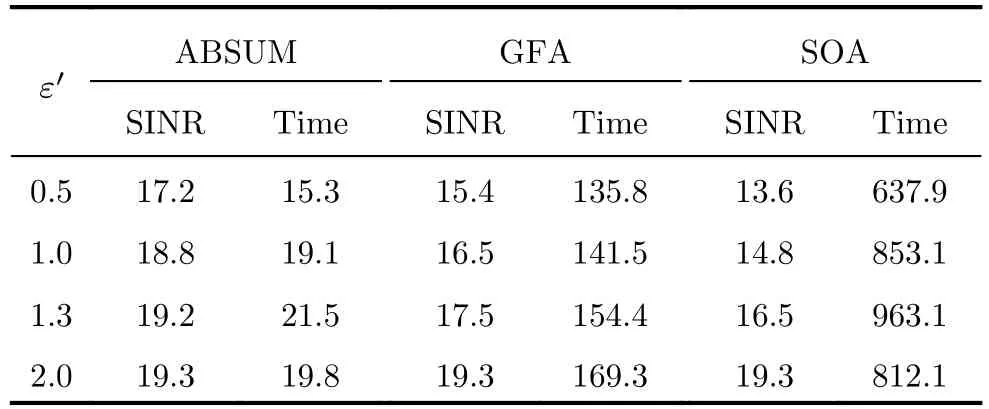
表2 ABSUM，GFA和SOA算法的优化SINR值(dB)和全局计算时间(s)Tab.2 SINR value (dB) and global computational times (s)for ABSUM，GFA and SOA

4.2 能量和相似性参数的影响

图3显示了当EI=10-5，10-4，10-2时，ABSUM，GFA和SOA算法的优化SINR值与相似性参数ε′的关系，结果再次表明ABSUM，GFA和SOA算法的优化SINR值随着相似度值的增加而增加，对于相同的频谱约束值，ABSUM可以获得比GFA和SOA更高的SINR值。此外，可以观察到，当ε′达到一定值时SINR不再变化，说明当相似性参数超过一定值时，相似性约束将消失。

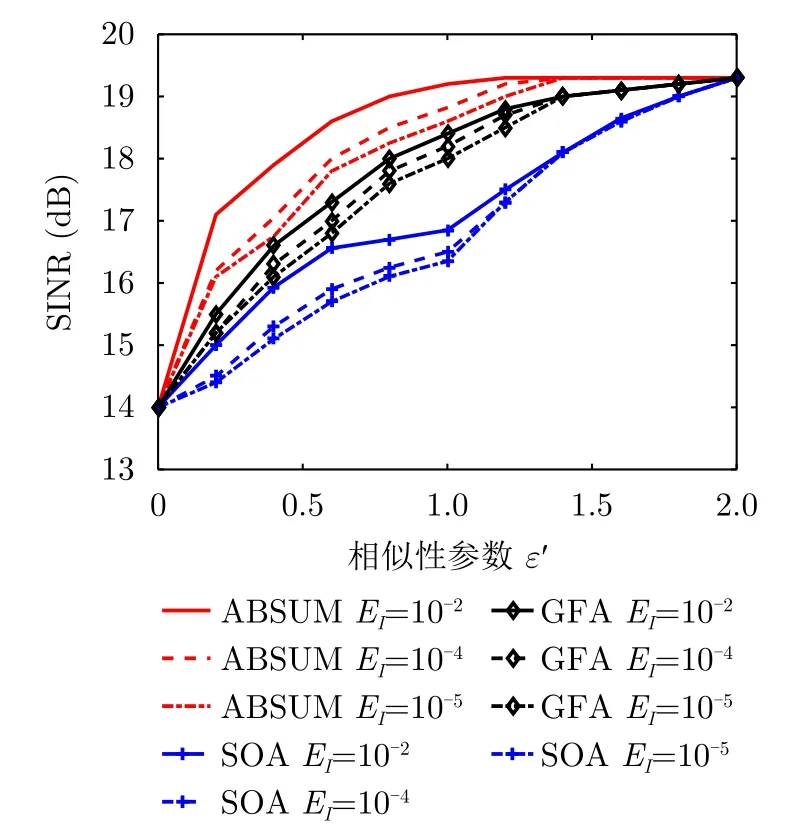
图3 ABSUM，GFA和SOA算法的优化SINR值和ε ′的关系(EI=10-2，10-4，10-5)Fig.3 The optimal SINR values of ABSUM，GFA and SOA versus ε′ with EI=10-2，10-4，10-5

假设相似度参数为ε′=0.5，1.0，2.0时，ABSUM，GFA和SOA算法的优化SINR值与频谱约束值之间的关系如图4所示，可以看出3种方法的优化SINR值随着EI的增加而增加，如所预料的那样，在相同的相似性约束条件下，ABSUM相比于GFA和SOA能获得更好的SINR性能。此外，可以看出当相似性参数ε′越大时，频谱约束对SINR的影响越小。特别是，当ε′=20时，频谱约束对SINR几乎没有影响。比较图3和图4可以发现，相似性约束对于SINR的影响要明显比频谱约束大得多。因此，设计现代雷达系统时，应该充分考虑相似性约束和频谱约束的权衡。

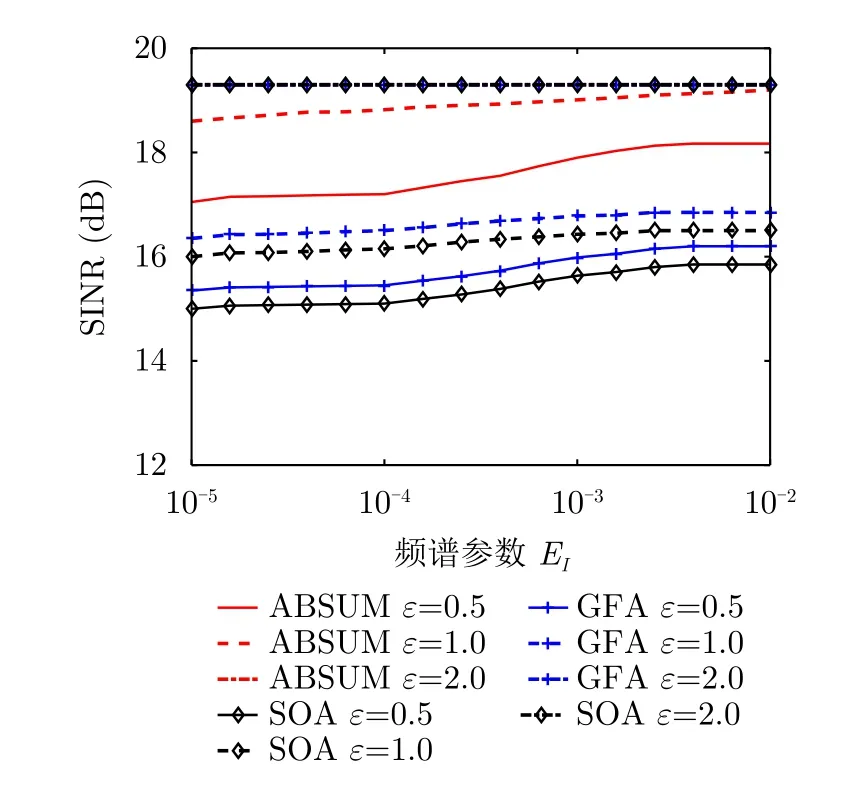
图4 不同频谱约束 EI下优化SINR值与相似性约束的关系(ε′=0.5，1.0，2.0)Fig.4 The optimal SINR values of ABSUM，GFA and SOA versus EI with ε′=0.5，1.0，2.0

图5显示了ABSUM算法和GFA算法的优化SINR值与不同频谱约束EI和相似性约束ε′的关系。正如预期那样，对于固定的相似性约束和频谱约束，ABSUM具有更好的SINR。另外，两种算法的输出SINR均与输入SNR呈线性关系。这意味着输入SNR对输出SINR损耗没有影响。

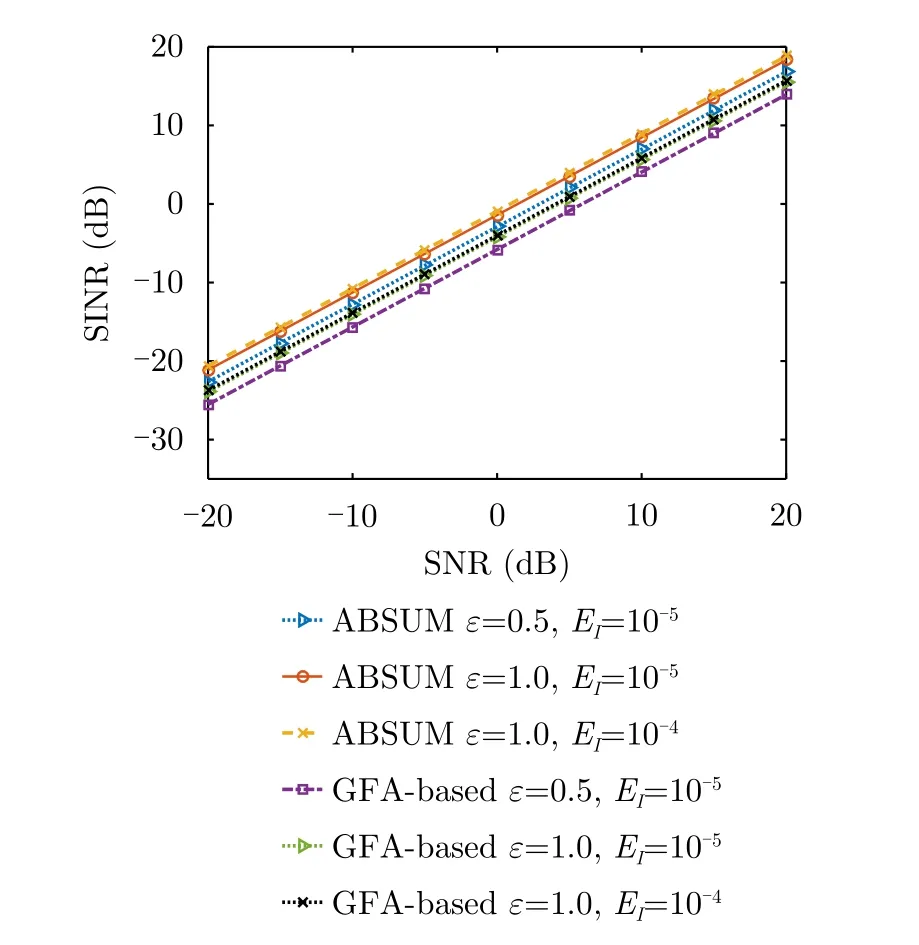
图5 ABSUM和GFA算法的输出SINR与EI和ε ′的关系Fig.5 The output SINRs of the proposed ABSUM and GFA versus the input SNR for different EI and ε′

接下来，讨论目标角θ0和干扰源角度θk，k=1，2，...，K不确定时SINR值的变化情况，首先假设δk=0，图6(a)表明当目标角度θ0的不确定性越大时，也就是δt越大时，将导致更大的SINR损耗。同样假设δt=0，由图6(b)可得，随着δk的增大SINR的损耗也越大。从图6可以看出，对于不同的EI和ε′，所提出的ABSUM算法比GFA算法具有更好的鲁棒性。

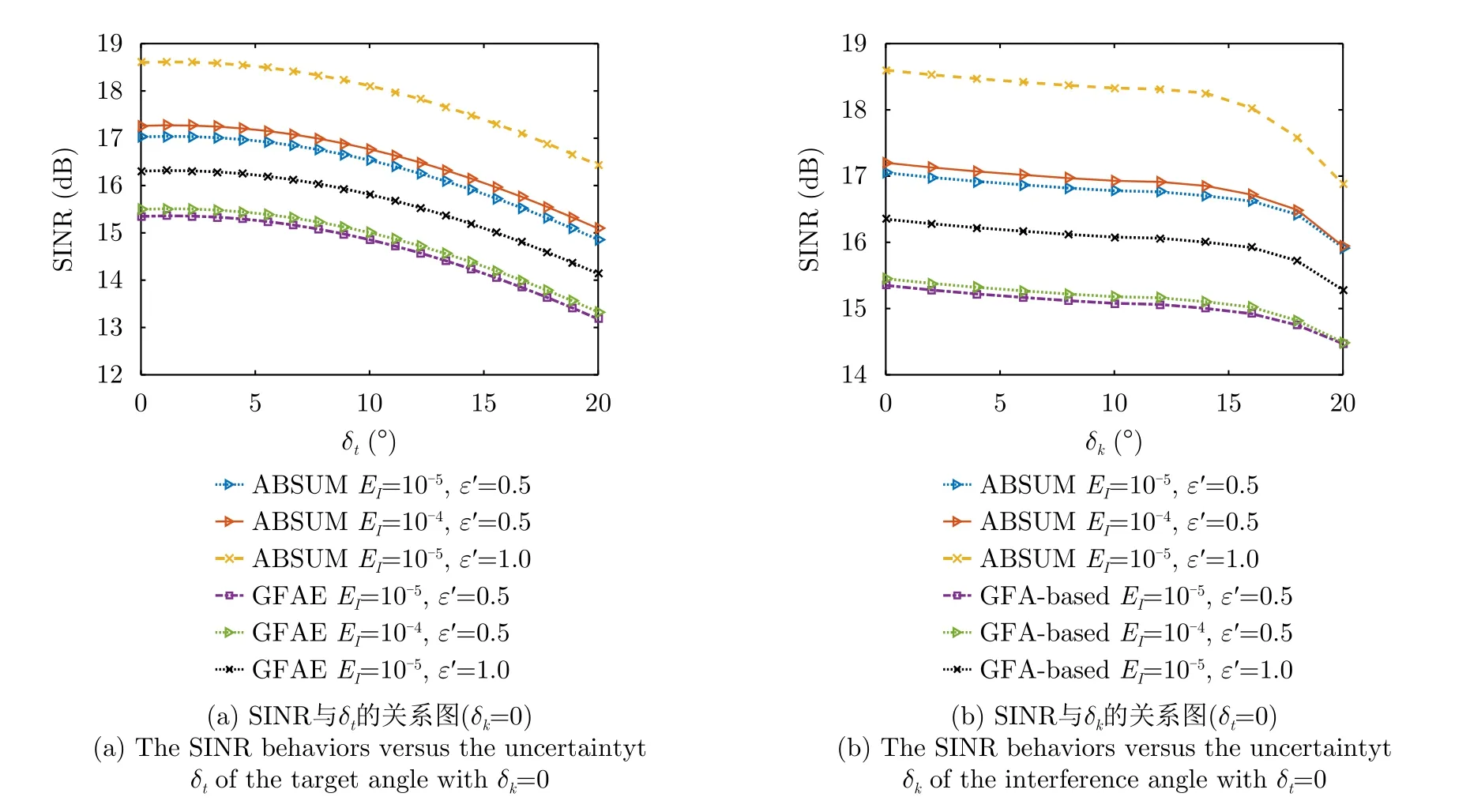
图6 SINR值与目标角和干扰源角度的关系图Fig.6 The SINR versus the uncertainty of the target angle and the interference angle

4.3 能量谱密度分析

关于频谱兼容约束，本文考虑两个共存的频率区间，第1个频率区间为=[0.2，0.3]，第2个频率区间为=[0.75，0.85]。首先假设相似性参数为ε′=1.0，图7提供了优化波形的能量谱密度(Energy Spectral Densities，ESD)和归一化频率的关系图。图7表明对应3个不同的EI值所优化的波形均在限制频段内产生了一定程度的频谱凹陷。限制频段内的波形功率谱主要受频谱约束EI的影响，当EI=10-4，10-3时，所设计的波形在2个限制频段内均形成较深的频谱凹陷，具有良好的频谱兼容性。对于较小的EI值，频谱凹陷更深，因为减少EI意味着在相应的阻带中传输更少的能量。但当EI增大到10-2时，限制频段内的频谱凹陷程度显著减小，这是因为频谱约束实质上是约束限制频段上的总能量，当频谱约束放松时，即EI值增加，所设计的波形仅需满足所有限制频段内的总能量不超过EI即可，在这种条件下可能会出现部分频段频谱凹陷消失的现象，但波形能通过更多的自由度来提升SINR值。

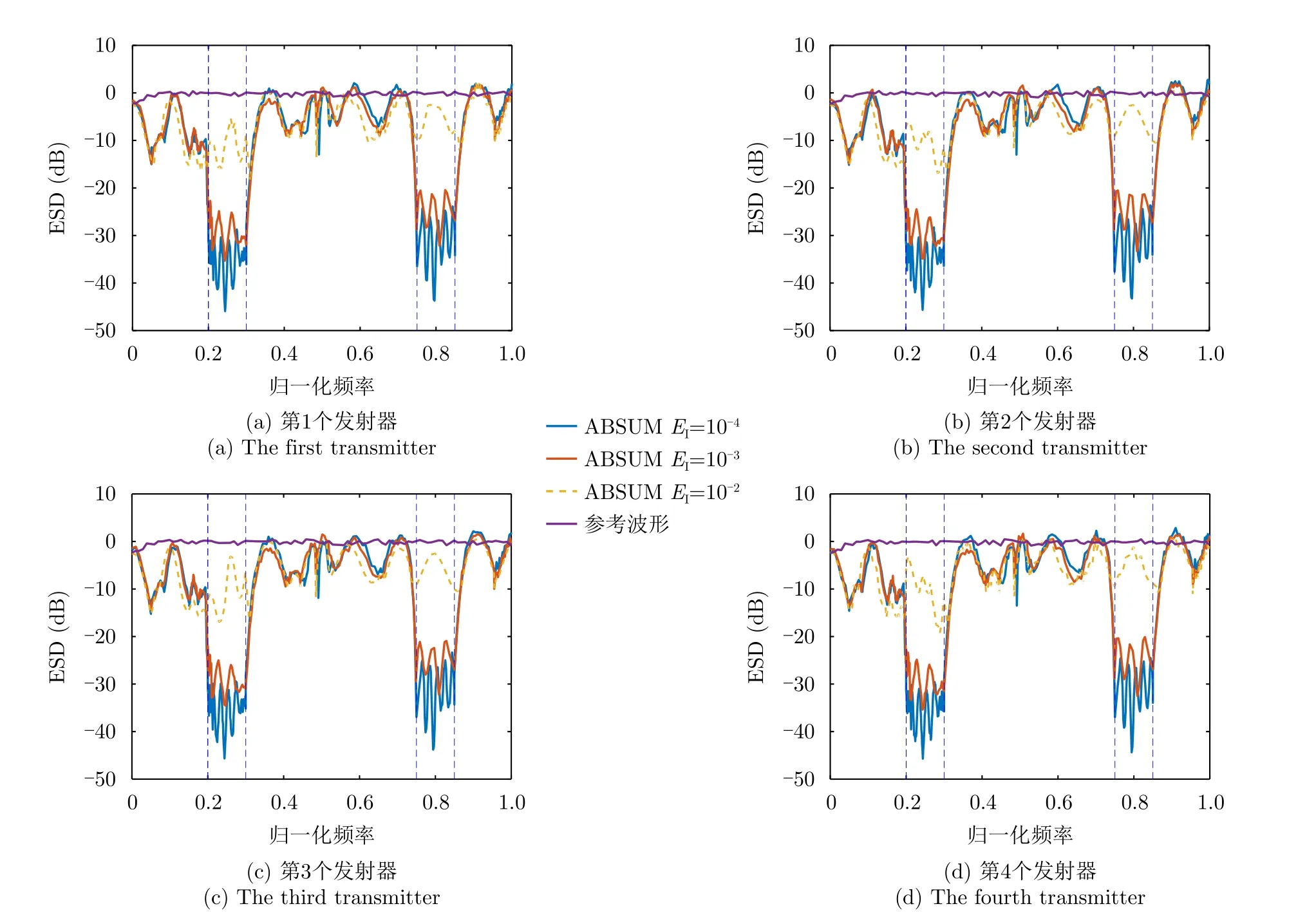
图7 波形功率谱图(ε ′=1.0)Fig.7 ESDs of the waveform optimized via ABSUM versus normalized frequency withε′=1.0

图8分析了在给定频谱兼容约束EI=10-4的条件下，不同相似性参数ε′优化波形的功率谱情况。对比图7可以发现，限制频段内的频谱凹陷变化情况受相似性约束的影响较小。相似性参数主要影响非限制频段区的功率谱形状，当相似性参数越小时，波形功率谱在非限制频段更加接近参考信号功率谱。最后，由图7和图8可得，限制频段内的功率谱分布主要受参数EI的影响，限制频段外的功率谱分布主要受参数ε′的影响。

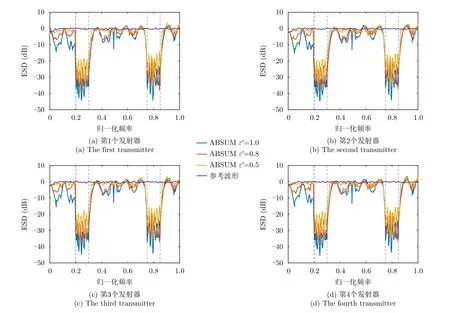
图8 波形功率谱图(EI=10-4)Fig.8 ESDs of the waveform optimized via ABSUM versus normalized frequency withEI=10-4

给定相似性参数ε′=1.0下，表3对比了不同算法在不同频谱约束EI的SINR值和全局计算时间。结果再次证实，所提出的ABSUM算法相比于SOA算法和GFA算法的SINR值有明显的提升，特别是当EI=10-2时，相比于SOA和GFA的增益分别为2.5 dB和2.4 dB。由于ABSUM算法是将原问题分解为多个子问题并行求解，能够更快地收敛到最优解，从表3中也可以看出全局计算时间明显小于SOA和GFA。相比于MM算法，全局计算时间略慢一些，在SINR增益方面有所提升，当EI=10-2时，提升约为0.1 dB。

表3 ABSUM、BCD、MM和GFA的SINR值(dB)和全局计算时间(s)Tab.3 SINR value (dB) and global computational times (s) for ABSUM，BCD，MM and GFA

4.4 波束图和模糊度函数分析

假设频谱兼容约束为EI=10-4，图9比较了不同相似值ε′=0.5，1.0，2.0下的ABSUM算法和GFA算法的波束图。波束图P(θ)的计算公式表示为P(θ)=|HH(θ)c|2，其中w˙是归一化滤波权重，即=w/‖w‖。从图9可以看出，对于所有参数ε′=0.5，1.0，1.2，本文提出的ABSUM算和GFA算法都具有良好的干扰抑制性能。然而，基于ABSUM算法波束图的主瓣增益要优于GFA算法。正如预期的那样，当ε′=2.0时，ABSUM算法和GFA算法表现出几乎相同的主瓣增益。

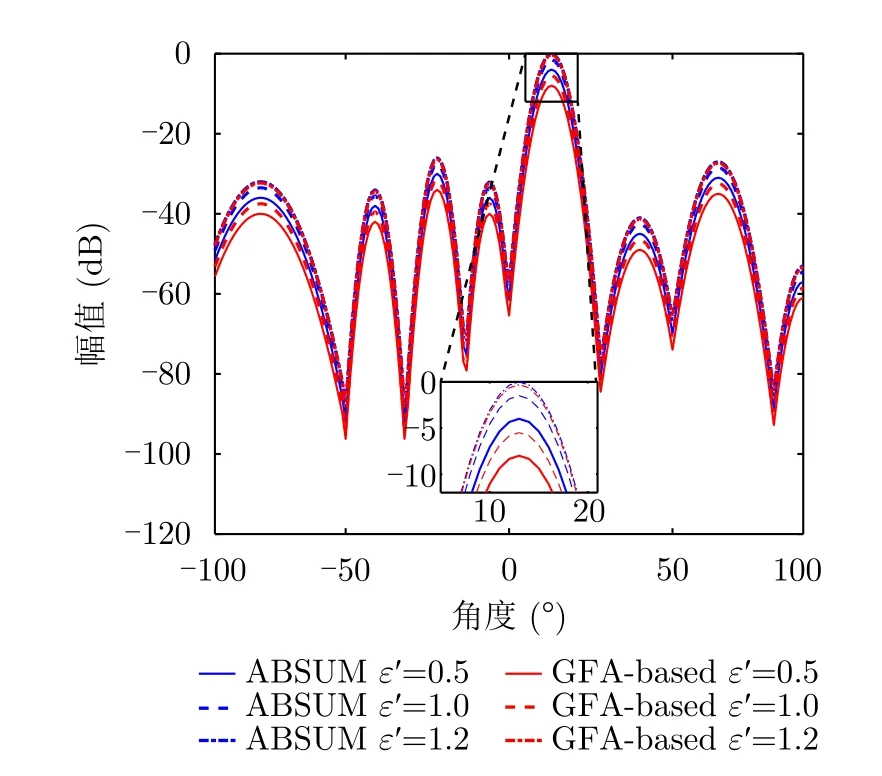
图9 频谱和相似性约束下的波束图(频谱约束EI=10-4)Fig.9 The beampatterns of the ABSUM and GFA with spectrum and similarity constraints (EI=10-4)

最后，本文利用互模糊函数(Cross Ambiguity Function，CAF)[19，39]来分析已优化雷达系统的联合距离和方位特征。图10(a)—图10(d)为不同频谱和相似性约束下CAF的距离-方位切割等高线图。假设频谱兼容约束为EI=10-4，图10(a)和图10(b)分别为算法1在迭代次数为0时(仅为接收机设计)和收敛时的模糊函数特征。距离-方位角图表明，与仅自适应接收不同，利用算法1优化的发射-接收对在收敛时，可以在黑色矩形中发现一个明显的峰值，它代表感兴趣的雷达目标。假设相似性约束为ε′=0.5，图10(c)和图10(d)分别显示了算法1在迭代次数为0时和收敛时的模糊函数特征。可以观察到相同的结果。这一现象表明，在频谱和相似性约束下，ABSUM算法都产生了合适的CAF，从而抑制了信号相关的杂波干扰。

算法1 基于ABSUM的发射和接收联合设计算法Alg.1 ABSUM algorithm for solving transmit-receive design

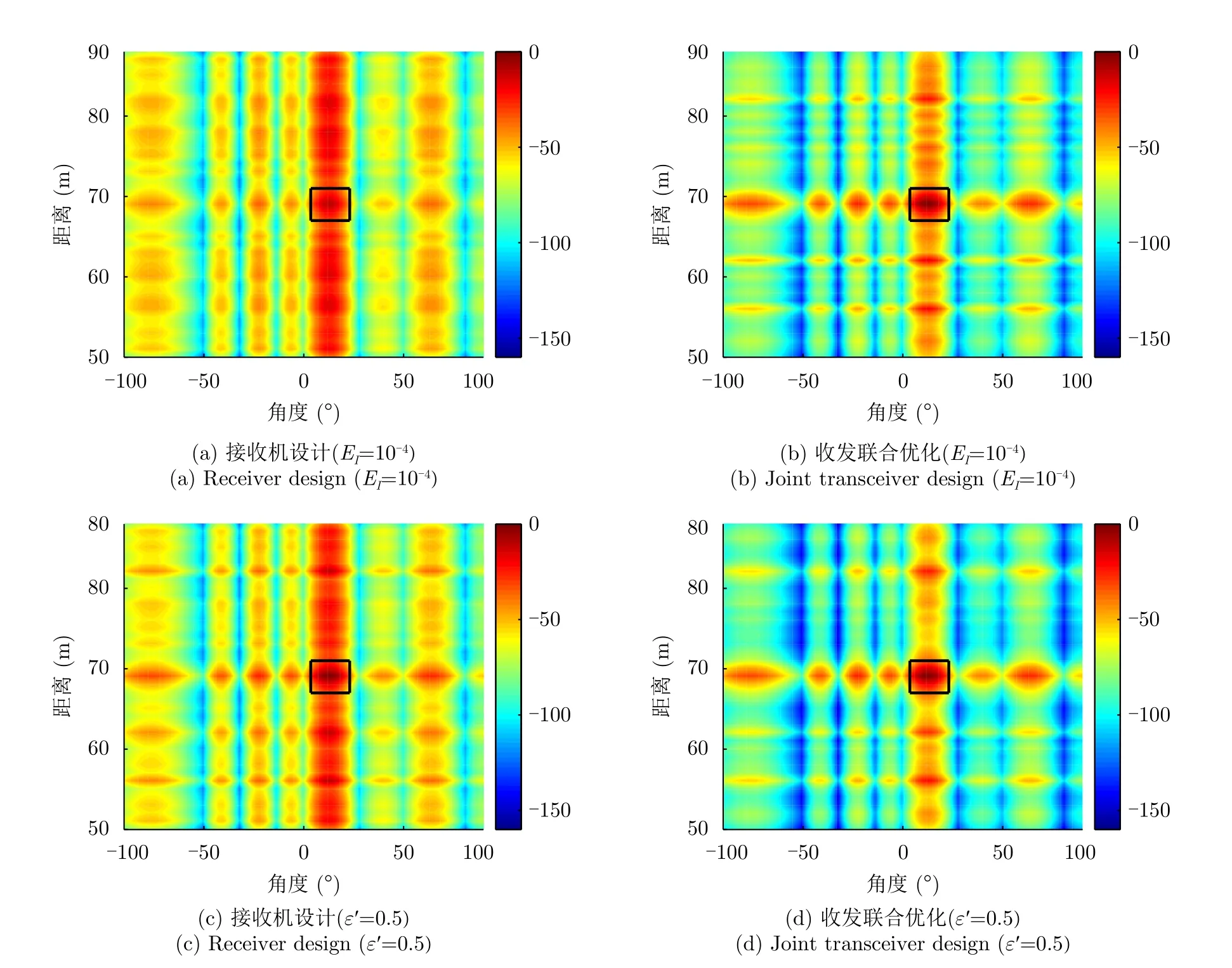
图10 MIMO模糊度函数的距离-角度切割Fig.10 Range-azimuth plane of MIMO CAF

5 结语

针对MIMO雷达系统和周边通信服务网络频谱兼容的问题，本文以发射波形能量、相似性和频谱兼容为约束条件，在信号相关杂波背景下，建立了MIMO雷达发射波形和接收滤波器的联合设计模型。为求解有非凸二次等式约束和二次不等式约束的优化问题，在ADMM框架下设计了一种基于BSUM算法的迭代原对偶算法，所提的方法结合了ADMM算法和BSUM算法的优点，通过数值仿真验证了该方法在输出SINR、频谱特征、波束图、计算复杂度和模糊特性等方面的性能。结果表明：(1)该算法以较低的计算代价实现了优于GFA算法的输出SINR。频谱兼容参数越小，输出SINR越小，相似度参数越小，输出SINR越小；此外，限制频段内的功率谱分布主要受频谱兼容参数的影响，限制频段外的功率谱分布主要受相似度参数的影响。因此，在实践中可以在输出SINR、相似性值和频谱兼容值之间进行适当的权衡。(2)与GFA算法相比，该算法对目标角度的不确定性和干扰具有更好的鲁棒性。此外，不确定性越大，导致的SINR损失越大。(3)在频谱和相似性约束下，该算法产生了合适的CAF，从而抑制了信号相关杂波的干扰。