基于交替方向惩罚法的低精度量化MIMO雷达恒模波形设计方法

万 环 余显祥 全 智 廖 斌*

①(深圳大学电子与信息工程学院 深圳 518060)

②(电子科技大学信息与通信工程学院 成都 611731)

1 引言

多输入多输出(Multiple-Input Multiple-Output，MIMO)雷达采用多信号同时发射与接收模式[1—3]，可按需调整发射波形，实现高增益窄波束或全区域覆盖的宽波束。相比传统相控阵雷达，MIMO雷达基于波形分集，可为系统发射与接收端提供更多的自由度，提高波达角(Directions of Arrival，DOA)估计精度、目标检测能力、干扰抑制能力[4—6]。MIMO雷达波形设计的一个主要目的是使发射能量集中在目标空间区域(主瓣)范围内，同时降低非目标区域(副瓣)能量辐射，实现波束能量的最佳匹配发射，从而提高雷达目标探测、参数估计和检测性能[7—9]。为了提升性能，MIMO雷达系统通常会配置大量有源天线单元，但采用高精度(超过10位)数模转换器(Digital-to-Analog Converters，DAC)组件会大幅增加系统电路的复杂度、能耗及成本。相反地，低精度DAC组件可以显著降低系统功耗与成本[10—12]，已广泛应用于各种场景，例如低功耗超宽带通信系统、大规模或超大规模MIMO系统[13，14]等。

现有的MIMO雷达波形设计方法主要面向采用高精度DAC组件的系统[15—20]，针对采用低精度DAC组件的MIMO雷达波形设计方法相对较少[21—26]。若直接对现有的基于无限精度DAC算法所设计的波形进行量化来适配低精度DAC组件，系统性能将会严重下降。低精度量化波形设计的核心难点在于离散相位或离散幅度的非凸约束求解。最直接的方法是采用穷搜法，但随着信号维度和快拍数的增加，计算复杂度与时间也呈指数量级增加。为了克服计算效率问题，目前主要有两类解决方法，第1类为改进式穷搜法，通过改变搜索策略与范围来减少搜索次数从而降低计算复杂度与运算时间。例如，文献[21]提出了基于块坐标下降(Block Coordinate Descent，BCD)搜索法，使搜索次数从指数级LNtN(L为低精度离散相位或幅度的个数，Nt为发射阵列天线数，N为快拍数)降低至TLNtN(T为该算法收敛时最大迭代次数)。基于此思路，文献[22]提出了两种广义似然上升搜索算法，第t+1次迭代结果可通过似然判断从第t次迭代结果翻转符号得到，进一步降低BCD算法的收敛迭代次数，但该方案仅对极低精度(1比特)波形有较好的求解效果。第2类将离散约束近似为连续函数进行求解，再将无限量化精度解重新量化或映射为低精度。文献[23]采用最小化积分副主瓣比(Integrated Sidelobe-to-Mainlobe Ratio，ISMR)准则，结合特殊的矩阵块结构，利用半正定松弛(Semidefinite Relaxation，SDR)技术，获得高精度发射信号，再通过量化器得到1比特信号。文献[24]采用连续可微函数来逼近1比特信号，并利用交替方向乘子法(Alternation Direction Method of Multipliers，ADMM)求得高精度解，再映射为1比特信号。基于文献[24]，文献[25，26]利用辅助变量与发射信号向量相互约束关系，将1比特信号的离散约束转换成区间连续约束，再通过ADMM算法使得信号不断逼近1比特后再映射为1比特，从而提高信号对1比特DAC的适配能力。

文献[23—26]考虑的是极低精度1比特波形，波形序列元素的实部与虚部的取值均为(E为发射波形总功率)，对应在极坐标轴上体现为有限个相位点(离散相位)，即{π/4，3π/4，5π/4，7π/4}。现有的低精度量化波形设计方法主要针对1比特，面向低精度多比特(2～5比特)的波形设计方法相对匮乏。另外，在雷达应用中，为了最大化发射机效率，防止发射机功放非线性失真，通常要求发射波形具有恒模特性，即每个码元的模值是恒定的[27—30]。因此，本文研究基于ISMR最小化准则的低精度(包括极低精度1比特)有限相位恒模波形设计方法。所建模的波形优化问题包含二次分式目标函数和非凸离散约束，难以求解。为此，本文提出了一种基于丁克尔巴赫交替方向惩罚法(Dinkelbach Alternating Direction Penalty Method，DADPM)的优化求解方法。该方法首先利用Dinkelbach算法[31]将目标函数二次分数形式转换成减法形式，再通过ADPM框架求解非凸离散相位约束问题，实现了低精度量化恒模发射波形设计问题的高效求解。

2 低精度量化恒模波形优化问题建模

即B比特恒模发射波形有L个相位均匀分布在以半径为q的极坐标圆周上。图2展示了1比特与2比特波形元素可行域。

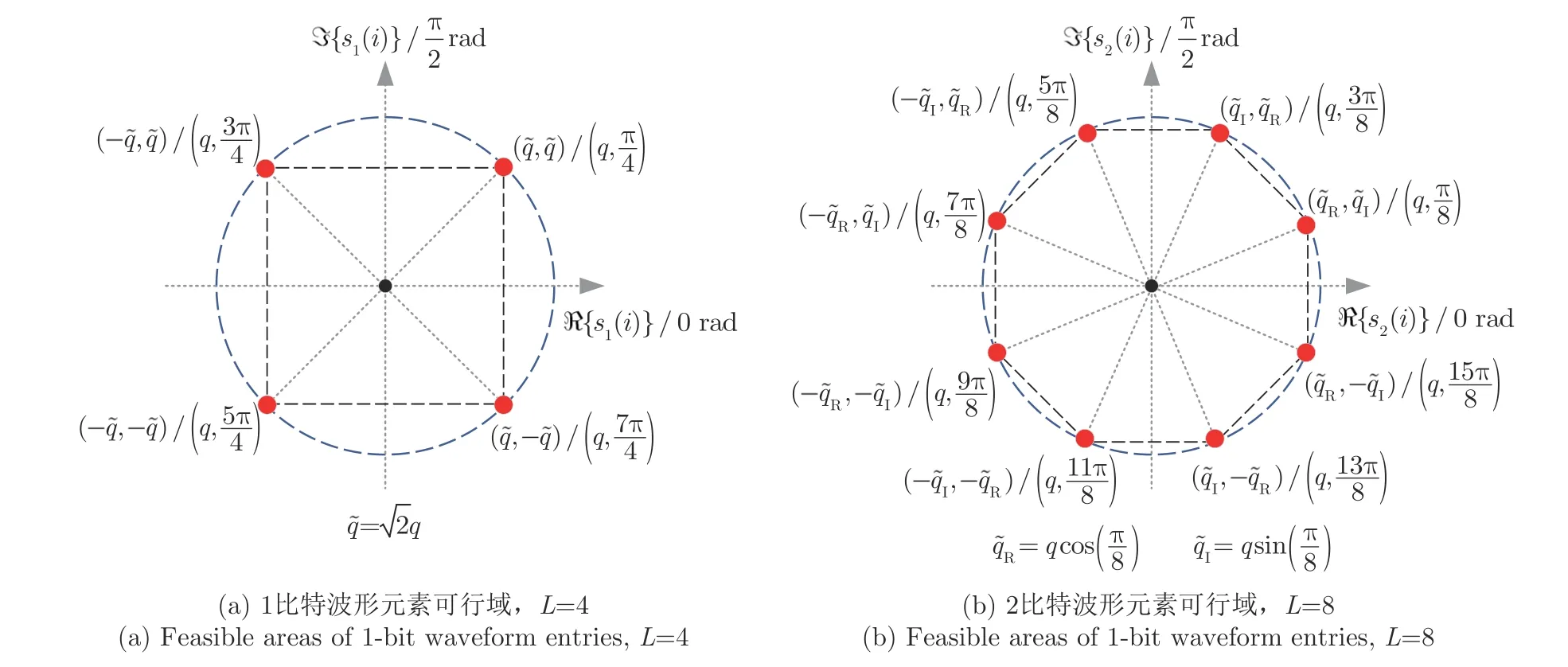
图2 1比特与2比特波形元素可行域(红点)Fig.2 Feasible areas of 1 bit and 2 bit waveform entries (red dots)

基于上述系统模型，在远场方向θ处，N个采样快拍下的信号可表示为[16]

当MIMO雷达发射相干波形，式(5)表示相控阵方向图。如果发射相互正交的波形，表明各个方向辐射的功率相等，实现了空域均匀覆盖。若发射相关波形，发射波束方向图取决于波形具体形式。

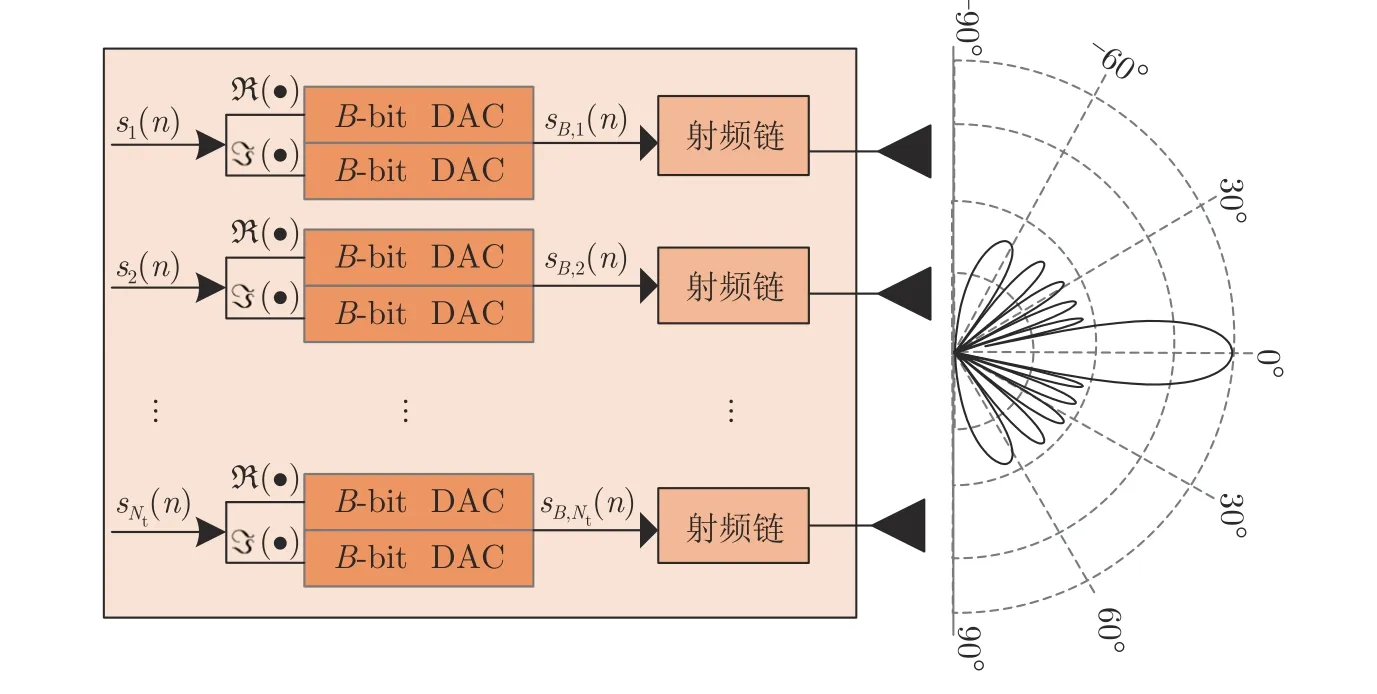
图1 配置低精度DAC组件的MIMO雷达发射端系统结构图Fig.1 System structure diagram of MIMO radar transmitter with low-resolution DACs

本文采用ISMR最小化准则来设计B比特恒模发射信号，因此该优化问题模型描述为

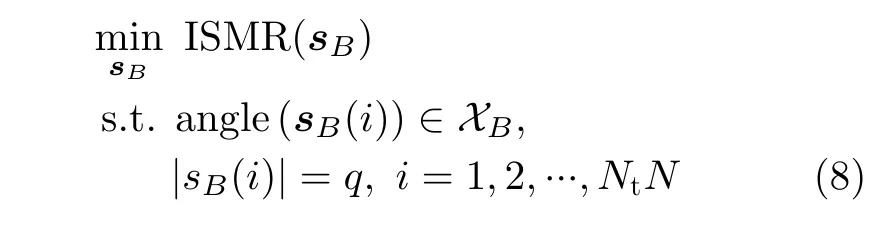
式(8)中，angle(·)表示输入变量的相位。上述问题的目标函数为二次分式，约束条件包含非凸离散相位约束，该问题为非确定性多项式-难(Nondeterministic Polynomial-hard，NP-hard)，难以求解。

3 问题求解

本节将提出一种基于ADPM的优化算法对问题(8)进行求解。该方法首先通过Dinkelbach算法将目标函数二次分数形式转换成减法形式，再基于ADPM框架，引入辅助变量，将离散相位约束转换为NtN个独立并行的三角函数问题，通过迭代逐步逼近最优解。

3.1 基于Dinkelbach算法的等价转化

基于Dinkelbach算法原理，可以将目标函数二次分数形式转换成减法形式，即

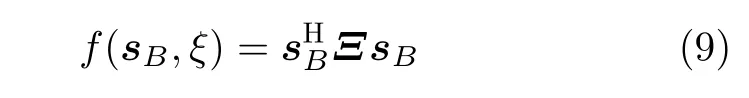
式中，Ξ表示为

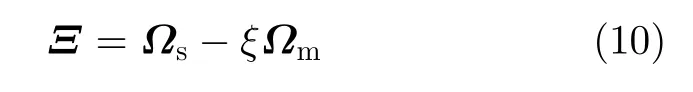
式中，参数ξ≥0，在Dinkelbach方法中通过式(11)不断更新：

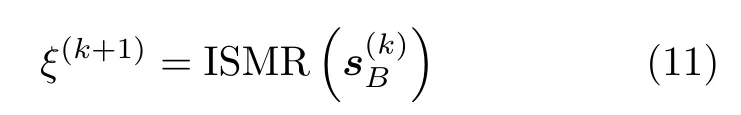
式中，k为迭代次数。这里需注意的是，Ξ可能不是正定矩阵。当Ξ为非正定矩阵时，对该矩阵进行对角加载，使其满足正定，即

问题(13)中约束条件包括离散相位约束以及恒模约束，可以利用ADPM算法[32]进行求解。

3.2 ADPM算法求解问题(13)

根据ADPM算法原理，式(14)的增广拉格朗日函数表达式为

3.3 ADPM算法迭代终止条件与初始值

根据文献[33]，可将迭代终止条件设置为

另外，初始值ϱ(0)会影响算法的收敛速度。文献[34]利用正则最小化和二次规划约束找到ADMM迭代收敛因子最小的最优初始值参数。本文采用的ADPM算法为ADMM算法的改进算法，对ADMM初始值的选取方式在ADPM算法中同样适用。因此，本文所根据文献[34]所提方法思想，将ADPM算法的惩罚因子初始值ϱ(0)设置为

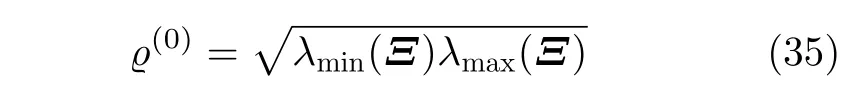
式中，λmax(·)表示矩阵最大特征值。

初始发射波形信号采用正交线性调频信号S(0)，S(0)矩 阵的第(m，n)个元素表示为

3.4 算法收敛性与复杂度

本文所提算法外层循环采用Dinkelbach法，内层循环采用ADPM算法，算法伪代码如表1所示。为分析算法的收敛性，首先证明序列{ξ(k)}是单调减小的。

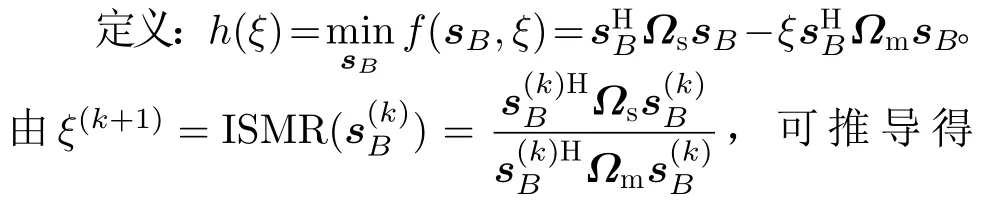
表1 丁克尔巴赫交替方向惩罚法的低精度量化MIMO雷达恒模波形设计算法Tab.1 MIMO radar constant modulus waveform design algorithm with low-precision quantized based on DADPM

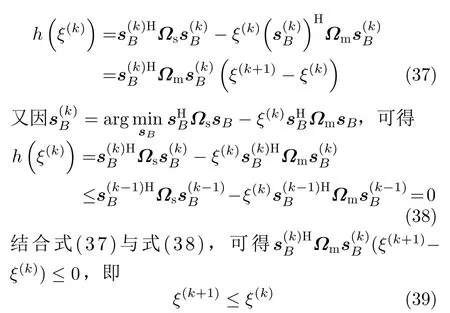
由式(39)得出，Dinkelbach法具有严格的单调性。内层循环采用ADPM算法，其中惩罚因子基于原始残差值动态更新，避免了传统ADMM算法在处理NP-hard问题时依赖惩罚因子初始值选取而存在不收敛问题，保证任意初始值情况下的收敛性[32]。综上，本文提出的DADPM算法中外循环Dinkelbach法具有严格的单调性，内循环ADPM算法具有强收敛性，可得出DADPM算法具有良好的收敛性。

4 数值仿真

为了方便算法性能分析，针对极低精度(1比特)量化的波形分析，本文提出的基于ADPM算法的1比特量化的波形(DADPM-1bit)对比了基于无穷比特(无量化/无相位约束)的ADMM优化算法设计的恒模发射波形[20](ADMM-∞bit)与该无穷比特波形直接运用符号函数量化后得到的1比特量化的波形(QADMM-1bit)。还对比了5种针对1比特量化DAC的设计方法，分别为：基于BCD算法的设计方法[21](BCD-1bit)、两种基于广义似然上升搜索算法的设计方法[22](GLAS1-1bit，GLAS2-1bit)、基于SDR算法的设计方法[23](SDR-1bit)、基于ADMM算法的1比特波形设计方法[25](ADMM1-1bit)。

针对低精度(2～5比特)量化波形，测试了主瓣对称与非对称情况下本文提出的基于DADPM算法的2～5比特量化的波形(DADPM-Bbit，B=2，3，...，5)性能，同时与基于ADMM优化算法的无穷比特恒模发射波形直接量化为2～5比特的波形(QADMM-Bbit，B=2，3，...，5)进行分析比较。

4.1 极低精度(1比特)量化波形性能分析

本节测试分析极低精度1比特量化波形的性能。对于1比特量化的波形，其B=1，相位符号数为L=2B+1=4个，根据式(2)计算，相位符号表示为{π/4，3π/4，5π/4，7π/4}。图3为极低精度量化的对称单主瓣波形序列相位分布图，展示了不同方法的相位分布情况。从图3可见，ADMM-∞bit算法波形序列元素的相位个数远远超过4个相位，其他本文测试的所有1 比特量化的波形方案相位均属于{π/4，3π/4，5π/4，7π/4}中。

图3 极低精度1比特量化的对称单主瓣波形序列相位分布图Fig.3 1-bit quantized waveform for single symmetrical mainlobe element phase diagram

极低精度1比特量化的波形对称单主瓣与双主瓣波形性能分别如图4和图5所示。图4(a)与图5(a)分别为1比特量化的对称单主瓣与双主瓣波形方向图，横坐标均为空间角度，纵坐标为发射信号在该方向上的平均功率，可通过式(5)计算得到。图4(b)和图5(b)分别为1比特量化波形的对称单主瓣与双主瓣ISMR与迭代次数k关系图，横坐标为迭代次数，纵坐标为系统ISMR。

从图4(a)可明显观察到，无穷比特的恒模方案(ADMM-∞bit)具有最低的副瓣，且主瓣区域较宽、有良好的增益，但该无穷比特波形直接量化为1比特波形后(QADMM-1bit)，副瓣明显提高，高于本文测试的所有基于1比特DAC设计的波形，且主瓣中心出现轻微下陷现象。相比另外5种基于1比特DAC设计的波形，本文所提方法具有最低的副瓣，在主瓣区间也有良好的增益。这种波形现象对应在波形ISMR表现为ADMM-∞bit具有最低ISMR，当该无穷量化精度波形直接量化应用在1比特DAC组件时(QADMM-1bit)，ISMR提高了将近11 dB，皆高于其他1比特波形的ISMR。本文提出的DADPM-1bit波形，相较于无穷比特波形，ISMR提高了大约6 dB，相较于其他1比特波形，ISMR值最低。

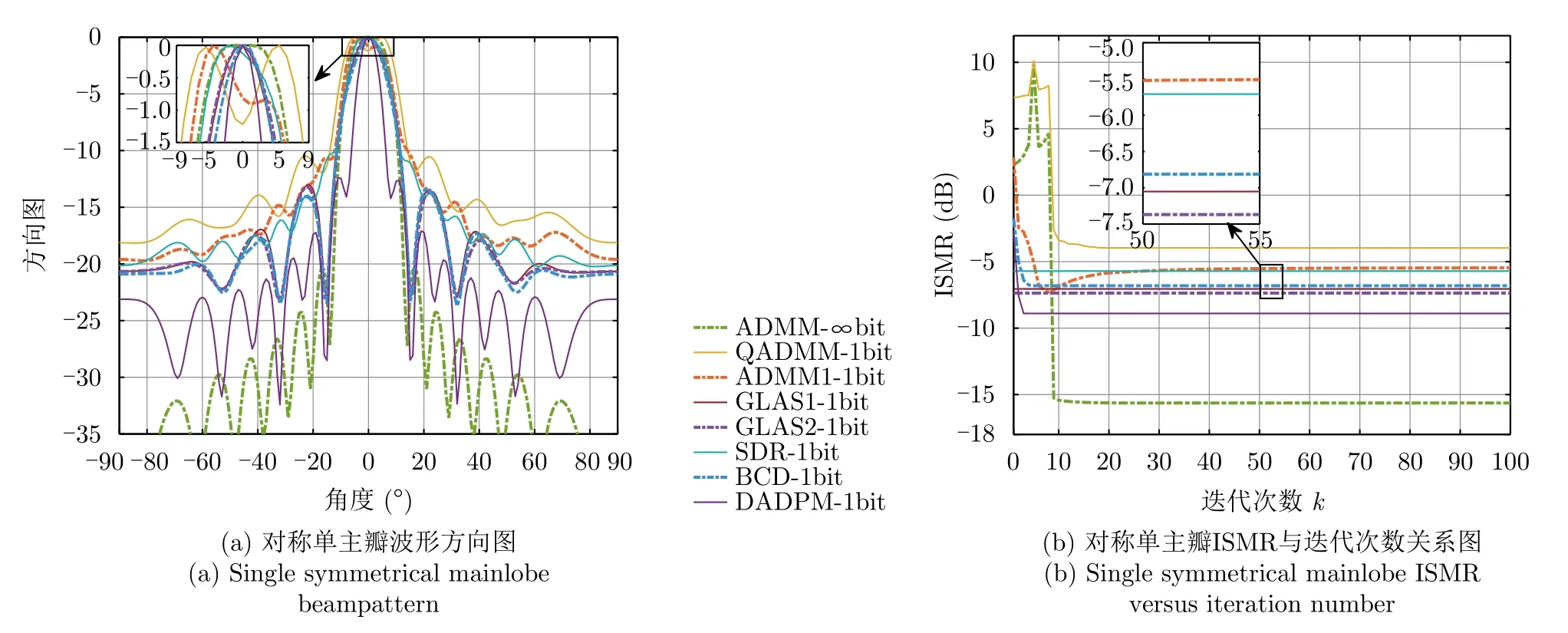
图4 极低精度1比特对称单主瓣波形方向图和ISMR与迭代次数关系图Fig.4 1-bit quantized waveform for single symmetrical mainlobe beampattern and the relationship between ISMR versus iteration number

从图5(a)可观察到，ADMM-∞bit波形具有最低副瓣，其他1比特量化算法波形方向图大致重合。因此，图5(b)中，ADMM-∞bit波形ISMR明显最低，其他1比特波形ISMR相差不大，但仍可以看出，无穷比特波形直接量化的QADMM-1bit波形的ISMR最高，本文提出的DADPM-1bit波形的ISMR最低。

图5 极低精度1比特量化的对称双主瓣波形方向图和ISMR与迭代次数关系图Fig.5 1-bit quantized waveform for two symmetrical mainlobe beampattern and the relationship between ISMR versus iteration number

表2为极低精度1比特量化的主瓣对称情况下不同算法1000次蒙特卡罗实验性能统计表。从表格运算时间可发现，相同条件下，SDR-1bit算法运算时间最长，GLAS1-1bit算法运算时间最短。本文所提DADPM-1bit算法性能明显优于其他极低算法性能，但运算时间相对较长。

表2 主瓣对称下极低精度量化波形算法性能统计表Tab.2 Performance statistics table of the extreme low precision quantized waveform algorithm for symmetrical mainlobe

4.2 低精度(2～5比特)量化的波形性能分析

本节测试分析了本文所提方法和基于ADMM优化算法的无穷比特(无相位约束)恒模发射波形与其直接量化为不同量化精度的低精度波形性能。测试的量化精度为2比特、3比特、4比特、5比特和无穷比特的ADMM算法。图6(a)与图7(a)分别为低精度2～5比特量化的对称单主瓣与双主瓣波形方向图。图6(b)与图7(b)分别为低精度2～5比特量化波形的对称单主瓣与双主瓣ISMR与迭代次数k关系图。

从图6(a)可明显观察到，ADMM方案经过低精度量化后，主瓣会出现中心下凹的现象，且本文所提方案明显比低精度量化后的ADMM方案具有更低的副瓣。图6(b)为对称单主瓣ISMR与迭代次数关系图，从图6可发现，相较于ADMM-∞bit波形，

本文所提DADPM-5bit波形ISMR差距约5 dB。与相同精度量化的ADMM波形相比，本文所提低精度量化的DADPM算法设计的波形具有更低的ISMR。

从图7(a)可观察到，本文所提低精度波形与量 化后的ADMM波形较为接近，主瓣大体重合，ADMM-∞bit波形具有较低的副瓣。从图7(b)可观察到，对称双主瓣时，相较于ADMM-∞bit波形，本文所提DADPM-5bit波形ISMR差距约1 dB。相同量化精度下，本文所提低精度量化的DADPM算法设计的波形比直接量化后的ADMM算法波形具有更低的ISMR。通过图6(b)与图7(b)可观察到，随着DAC量化精度提高，波束的ISMR减小，但ISMR下降的幅度值越来越小。

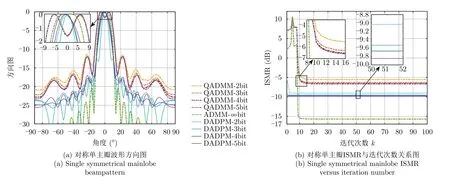
图6 低精度(2～5比特)量化的对称单主瓣波形方向图和ISMR与迭代次数关系图Fig.6 Low precision quantized waveform for symmetrical single mainlobe beampattern and the relationship between ISMR versus iteration number

图8为低精度(2～5比特)非称双主瓣波形方向图和ISMR与迭代次数关系图。从图8(a)可观察到，当两个主瓣不对称时，其中一个主瓣的峰值会下降，甚至主瓣区域内产生零陷。主要由于优化准则为最小化积分(离散累加和)副瓣与主瓣的比值，且矩 阵R(θ) 具有共轭性，使得Pt(θ)+Pt(-θ)=，因此，非对称情况下无法保证每个主瓣都有一个较高的峰值，而主瓣对称情况下，可使得两个主瓣都具有较好的增益，如图5(a)与图7(a)。从图8(b)可观察到，主瓣非对称时，ADMM-∞bit波形直接量化后，ISMR值提高超过6 dB以上，而本文所提2～5比特低精度DADPM波形与ADMM-∞bit波形的ISMR相差约1 dB。

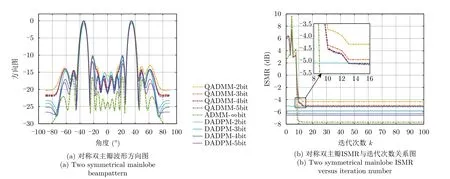
图7 低精度(2～5比特)量化的对称双主瓣波形方向图和ISMR与迭代次数关系图Fig.7 Low precision quantized waveform for two symmetrical mainlobe beampattern and the relationship between ISMR versus iteration number

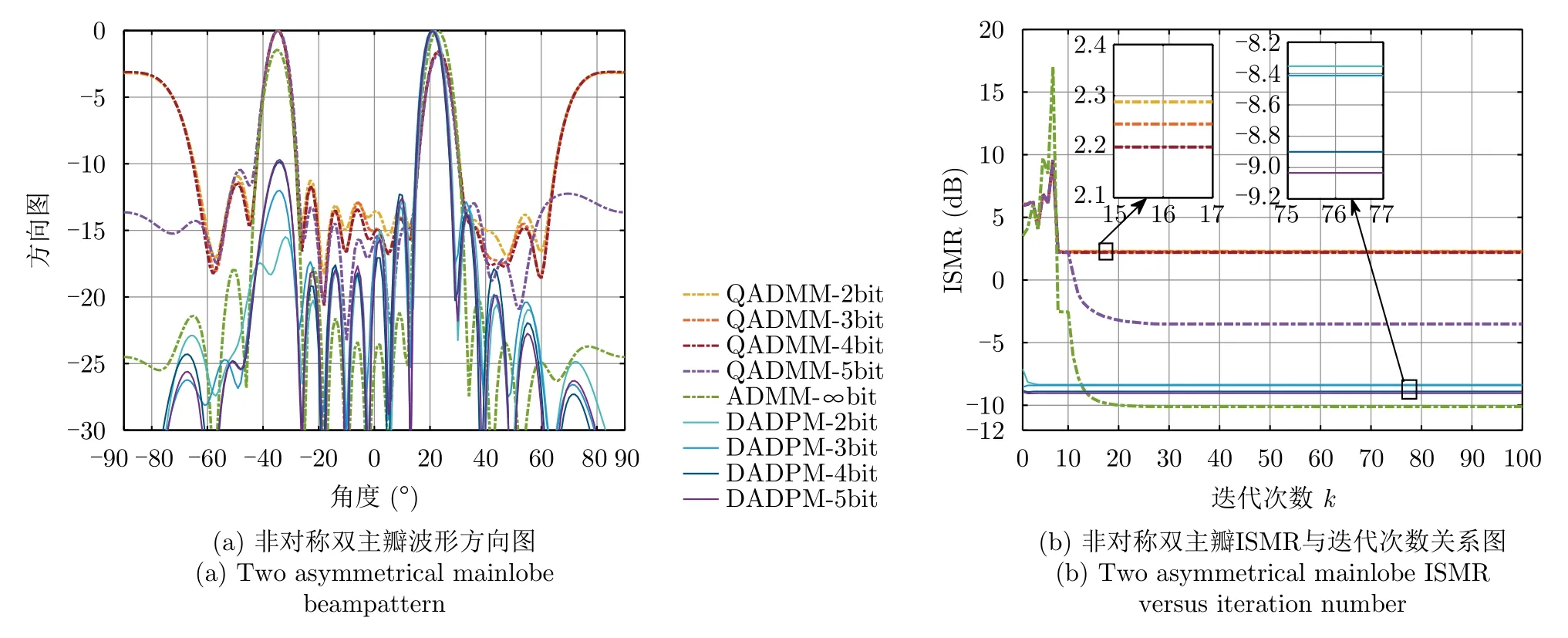
图8 低精度(2～5比特)量化的非称双主瓣波形方向图和ISMR与迭代次数关系图Fig.8 Low precision quantized waveform for two asymmetrical mainlobe beampattern and the relationship between ISMR versus iteration number

表3为低精度量化的对称主瓣波形算法在1000次蒙特卡罗实验下的性能统计表。从表3运算时间可发现，本文所提DADPM算法，不同精度对算法的运算时间没有太大影响，精度越高波形ISMR越小。DADPM算法的ISMR明显低于同精度量化的ADMM算法，但DADPM算法运算时间明显长于同精度量化的ADMM算法。主要是因为内循环采用的ADPM算法在迭代的同时动态更新惩罚因子，从而保证算法的收敛性。而ADMM算法惩罚因子直接根据设计人员经验或者实验总结给定，省略了算法寻找合适惩罚因子的过程，算法运算时间更短，但算法性能表现过于依赖惩罚因子。

表3 低精度量化的对称主瓣波形算法性能统计表Tab.3 Performance statistics table of the low precision algorithm for symmetrical mainlobe

5 结语

本文提出了一种基于低精度量化的MIMO雷达发射波形设计方法。通过设计B比特恒模发射波形序列，使发射波形对低精度量化DAC组件有更好的适配性，实现任意精度波形的最佳匹配发射。为解决所建模的恒模离散相位约束非凸优化问题，首先通过Dinkelbach算法将二次分式转换成减法形式，再运用ADPM算法框架，将离散相位约束转换为并行的三角函数问题，通过交替迭代逐步逼近最优解。低精度DAC组件可降低MIMO雷达电路结构复杂度与能耗，但这些低精度组件也会导致一定程度的性能下降。本文所提出的低精度恒模发射模型设计方法可适用于任意量化精度的发射波形设计，相对其他低精度设计方法，取得了更低的ISMR性能表现，可为实际工程应用中对波形性能要求与DAC量化精度的选择提供理论依据与参考价值。