基于波形优化和天线位置选择的MIMO雷达波束扫描算法研究

范 文 蔚保国 陈 镜 张 航③ 李淳泽

①(中国电子科技集团公司第五十四研究所 石家庄 050081)

②(卫星导航系统与装备技术国家重点实验室 石家庄 050081)

③(西北工业大学电子信息学院 西安 710072)

1 引言

集中式多输入多输出(Multiple-Input Multiple-Output，MIMO)雷达通过不同发射天线发射不同探测波形形成特定的发射方向图，良好的发射波束图可有效降低杂波对雷达系统的干扰和提高雷达系统对波达方向不精确已知目标探测的鲁棒性[1—7]。在雷达应用中，雷达天线通常会辐射多种不同的波束图(如波束扫描)来满足不同探测任务的需求[8—13]。通常集中式MIMO雷达通过发射不同的探测波形集实现发射波束的变化，但当集中式MIMO雷达系统使用稀疏天线阵时1雷达天线单元间间距不同，且有可能大于半波长。，传统的MIMO雷达发射波束图合成方法，如文献[1—4]，因仅考虑均匀线阵(Uniform Linear Array，ULA)配置而无法满足多波束变化要求，而现有MIMO雷达稀疏天线阵设计技术因为在设计中只合成一个波束，如文献[14—16]，使得其在多波束的应用场景中可能不是最佳的。本文就MIMO雷达天线位置选择的多波束扫描算法展开研究。

集中式MIMO雷达发射波束图合成的研究工作可分为两类。第1类采用两步策略，即首先优化波形协方差矩阵形成特定的发射波束图[4，11，12，17]，然后根据得到的协方差矩阵设计一组雷达发射波形[18，19]。例如，文献[4]提出了一种最小旁瓣波束图设计准则优化波形协方差矩阵，然后利用循环算法优化具有理想PAPR的MIMO雷达探测波形[16，18]。文献[11]基于加权最小二乘波束图匹配准则优化具有特定发射波束图的波形协方差矩阵。其他两步设计方法详见文献[12，17，19—21]。通常这种两步策略存在很大拟合误差。第2类是直接设计波形合成预期的发射波束图以避免两步法的拟合误差问题[3，5，13，22]。例如，文献[5]提出了一种连续闭式解的方法来优化恒模探测波形。文献[22]基于最小二乘波束图匹配准则直接优化波形，并利用半定松弛(SemiDefinite Relaxation，SDR)方法求解4次优化问题，但该方法计算复杂度太高，难以满足实际应用需求。文献[3，23，24]提出了基于交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)的恒模波形设计方法。其他直接设计方法可参考文献[13，25—28]。

目前也有学者研究了集中式MIMO雷达发射波束图合成的天线位置选择方法，如文献[14，15，29]，但这些研究只考虑了波形协方差矩阵的优化，没有设计波形。此外，上述研究在其设计中只考虑合成一个发射方向图，使得该方法所选天线位置对于多波束图任务可能不是最优的[30]。虽然文献[8，31，32]提出了稀疏天线阵的多波束合成技术，但这些方法只适用于相控阵，因为集中式MIMO雷达波束图与其每个发射天线所发射的波形密切相关，通常要考虑如恒模、峰值均公比(Peak-to-Average Power Ratio，PAPR)等波形约束[33—38]，使得此类技术不能直接用于集中式MIMO雷达。基于此，本文提出MIMO雷达的多组探测波形和天线位置联合优化技术，满足现实中雷达波束扫描任务和天线位置优化。本文贡献总结如下：

(1) 提出多组探测波形和天线位置联合优化的波束图匹配设计方法，以实现MIMO雷达波束扫描任务。本文设计准则可以实现具有等纹波特性的发射波束图，即保证得到的波束图的旁瓣处于同一电平，主瓣电平波纹相同。文献[13，39—41]指出，波束图的这种等纹波特性可提高雷达系统对方向不精确已知目标探测的鲁棒性，还可降低雷达杂波对雷达系统的影响；与文献[8，14，15，31，32]不同，本文直接设计多组探测波形，在合成多波束的同时优化集中式MIMO雷达的天线位置。

(2) 由于天线位置参数以指数形式存在于阵列导向矢量中，直接优化天线位置参数十分困难。为有效克服这一难题，本文假设一定数量的天线位置可用于天线放置，然后引入布尔类型选择向量，将天线位置优化问题转化为天线位置选择问题，有效降低了问题建模的复杂度。

(3) 基于本文的设计准则所形成的优化问题是非凸、非光滑、大规模的NP-难问题。为有效求解此问题，首先，本文采用Lawson算法[42—44]将minmax问题转化为迭代加权最小二乘(Iterative weighted Least Squares，ILS)问题；然后，本文结合ADMM[45—47]和MM (Majorization-Minimization)[48—51]提出了一种组合优化技术，即Majorization-ADMM (M-ADMM)来简化和求解转化后的约束ILS优化问题。

符号定义：(·)*，(·)T以及(·)H分别表示复共轭、转置和共轭转置。IN表示维度为N×N的单位矩阵。Xn，l，Xn，:，X:，l分 别表示矩阵X对应的第(n，l)个元素、第n行以及第l列。diag(a) 表示由向量a=[a1，a2，...，an]T构成的对角方阵。R e[·]表示给复数取实部操作符。|·|表 示取模操作符。‖·‖2和‖·‖F分别表示欧氏范数(Euclidean norm)和F范数(Frobenius norm)。其他符号在首次出现后定义。

2 问题建模与求解

2.1 系统模型

2.2 天线选择

2.3 优化模型

在雷达应用中，雷达天线通常需要辐射多种不同的波束图(如波束扫描)以满足不同的探测任务[8—13]。集中式MIMO雷达可通过发射不同的探测波形实现发射波束的变化，但当集中式MIMO雷达系统使用稀疏天线阵时，传统的MIMO雷达发射波束图合成方法，如文献[1—5，8—13]，因仅考虑ULA配置而无法满足设计要求，而现有基于天线选择的MIMO雷达波束图设计技术因为在设计中只考虑合成一个波束，如文献[14，16，19，29]，在生成多个波束的应用场景中可能不是最优的。为此，本文在优化集中式MIMO雷达天线位置的同时优化多组探测波形集以保证集中式MIMO雷达的多波束变换能力。

2.4 算法推导

可以看到，通过辅助变量的引入，优化问题(13)的目标函数中变量受限于线性约束Zi=diag()Xi，而PAPR约束和布尔类型约束分别与变量Xi和相关。

对于优化问题目标函数中的m ax操作和非凸问题，Lawson算法(参考文献[42，43，48])指出min-max优化问题的解可以通过求解一系列加权最小二乘问题获得。

例如，针对优化问题

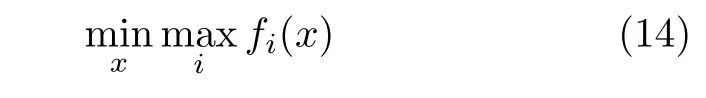
Lawson算法通过迭代的方式求解，步骤如下：

步骤1 将min-max优化问题写为如下加权最小二乘问题，并求解该问题获得x(t)：

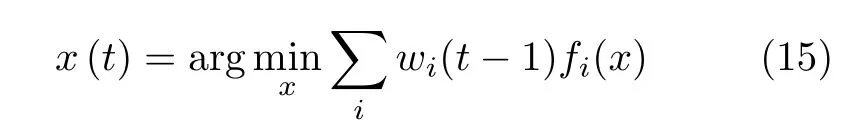
步骤2 按如下规则更新权值

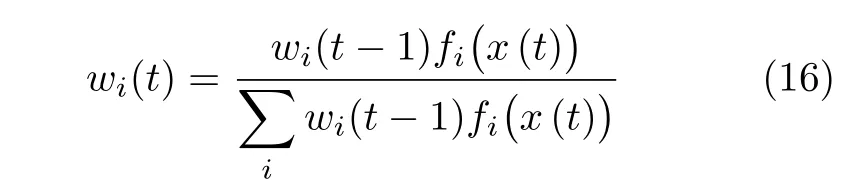
重复上述步骤，直至算法达到收敛条件。

下面根据Lawson算法处理优化问题(13)目标函数的非光滑性。首先，将优化问题(13)写为

那么优化问题(17)的目标函数在点Zi=Zi(t)，∀i处的上界函数为

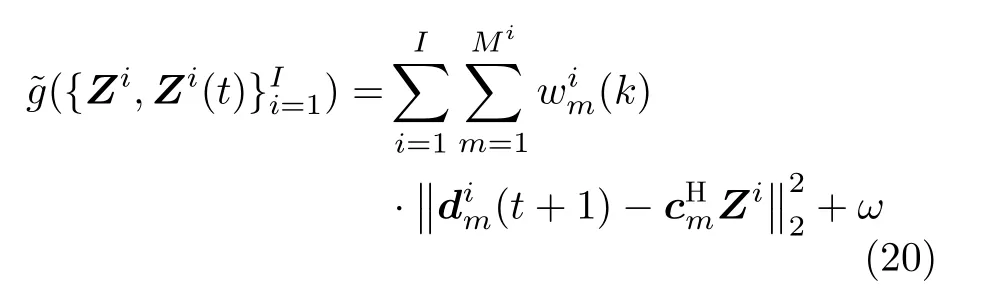
其中，ω为常数。

证明：

优化问题(17)的目标函数可写为

本文用ADMM求解优化问题(17)对应的上界优化问题(27)，而非直接利用ADMM求解(17)，因此，将上述求解方法称为M-ADMM(感兴趣的读者请见文献[52])。下面给出优化问题(29)和(30)的求解方案。

2.4.1 优化问题(29)的求解

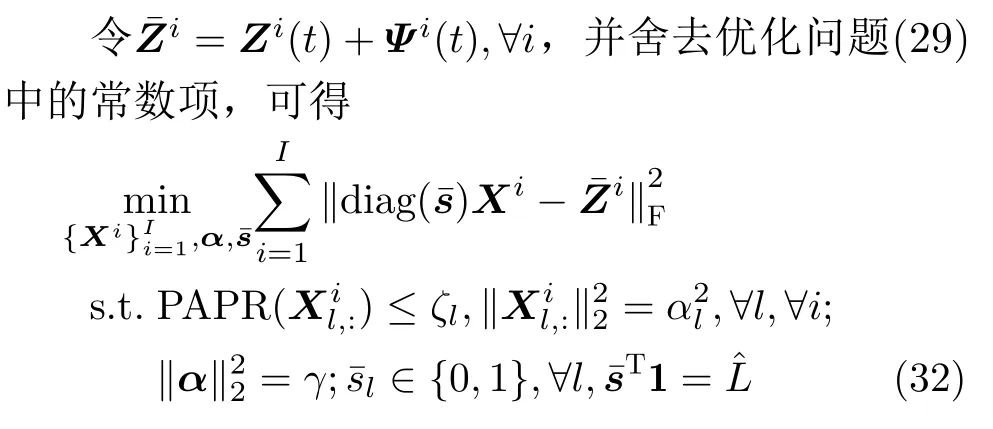
3 复杂度分析

表1 基于波形优化和天线位置选择的MIMO雷达波束扫描算法Tab.1 Algorithm for joint waveform optimization and antenna position selection for MIMO radar beam scanning

4 仿真实验

图1(a)—图1(c)分别给出了波束图合成结果、优化问题目标函数值(Objective Function Value，OFV)随算法迭代次数的变化曲线以及最优天线位置结果；从图1(a)可以看到16个波束图具有几乎相同的波束图旁瓣水平，且每个波束图的旁瓣水平几乎相等，表明了本文min-max设计准则的有效性；从图1(b)可以看到，经过大约200次迭代后，目标函数值几乎保持不变，算法收敛；从图1(c)可以看到，优化后天线单元的位置已经不再是等间距的，具有稀疏结构。

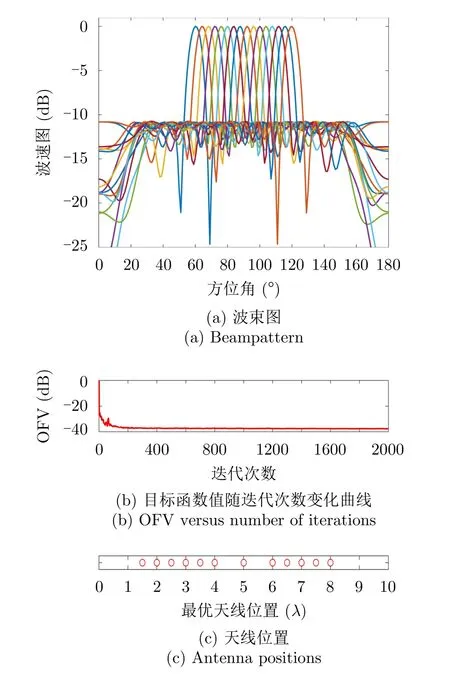
图1 仿真样例1Fig.1 Simulation example 1

图2(a)和图2(b)分别绘制了样例1中目标函数值随算法运行时间的变化曲线以及M-ADMM迭代总次数和算法外迭代次数的变化关系，由图2(a)可以看到大约40秒后目标函数值基本保持不变，算法达到收敛。图2(b)可以看到随着外迭代次数的增加，M-ADMM迭代的次数也趋于减小(从最大73次，逐渐减少到1次)，并且最后保持到仅需1次迭代。结合图1(b)和图2(b)结果可以看到随着迭代进行算法逐渐收敛，且算法内迭代次数也趋于减少，大约200次外迭代后算法收敛。图2结果表明，虽然本文算法单次迭代复杂度较高，但M-ADMM的快速收敛性使得本文算法在实际中依然有很好的实用性。

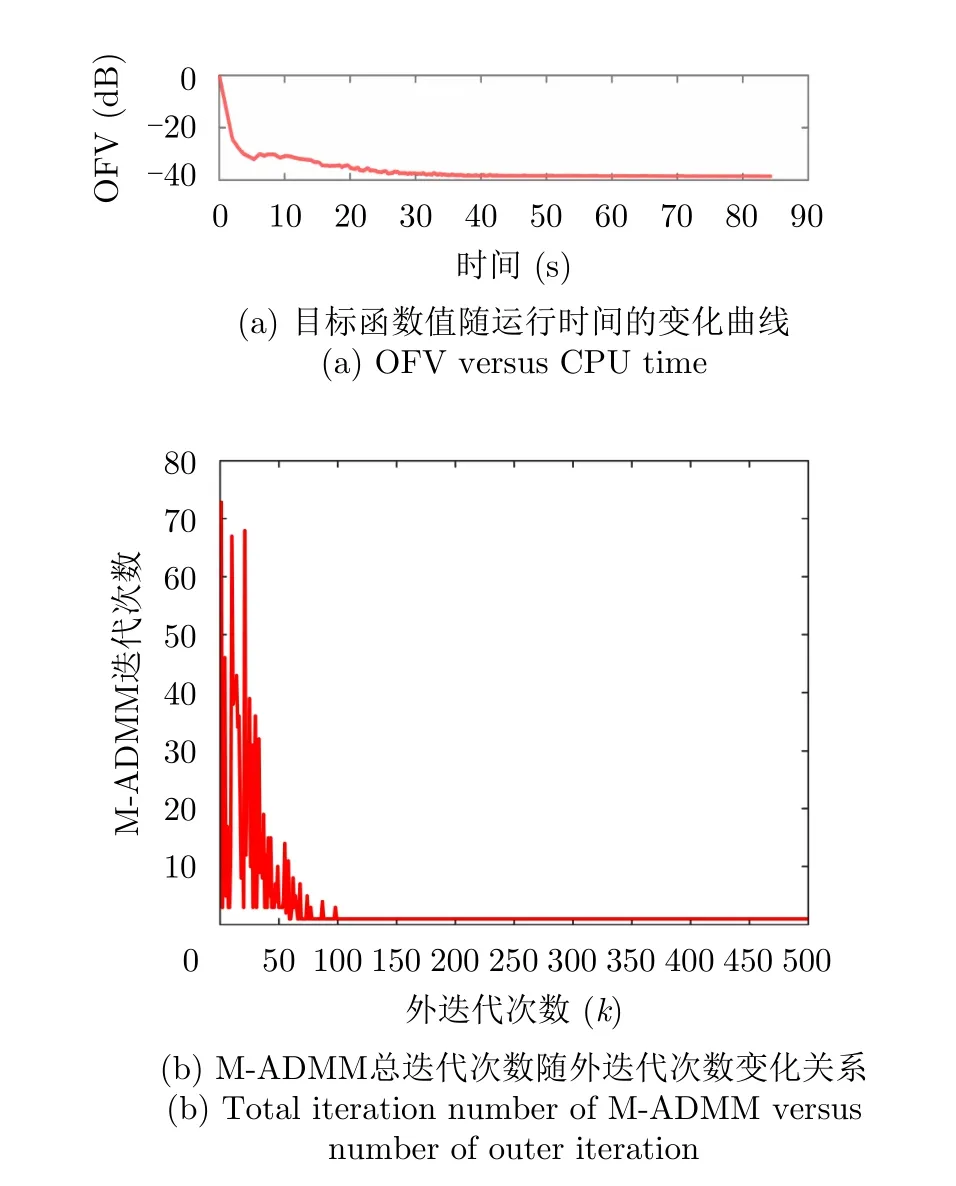
图2 收敛性分析Fig.2 Convergence performance analysis

图3(a)—图3(c)分别绘制了波束图合成结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果；从图3(a)可以看到16个波束图具有几乎相同的波束图旁瓣水平和相同的波束图旁瓣零陷(—30 dB)，达到了设计要求的比峰值旁瓣低—20 dB的零陷，且每个波束图的旁瓣水平也几乎相等，再次表明了本文min-max设计准则的有效性；从图3(b)可以看到，经过大约60次迭代后，目标函数值几乎保持不变，算法收敛；从图3(c)可以看到，与实验样例1相同，优化后天线单元的位置具有稀疏结构。

图4(a)—图4(c)给出了天线位置数L=17，天线数=12时本文方法的波束图结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果；相比于图3(a)，图4(a)波束图的峰值旁瓣增大了1 dB左右，主要因为可用天线位置减少了(稀疏孔径相同)，使得波束图合成的灵活度也相应地降低了，导致了波束图旁瓣的增大。

图5(a)—图5(c)给出了天线位置数L=20，天线数=15时本文方法的波束图结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果；相比于图3(a)，图5(a)波束图的峰值旁瓣降低了3 dB左右，主要因为可用天线数量增加了(稀疏孔径增大了)，波束图合成的灵活度也相应的增加了，使得波束图旁瓣降低。

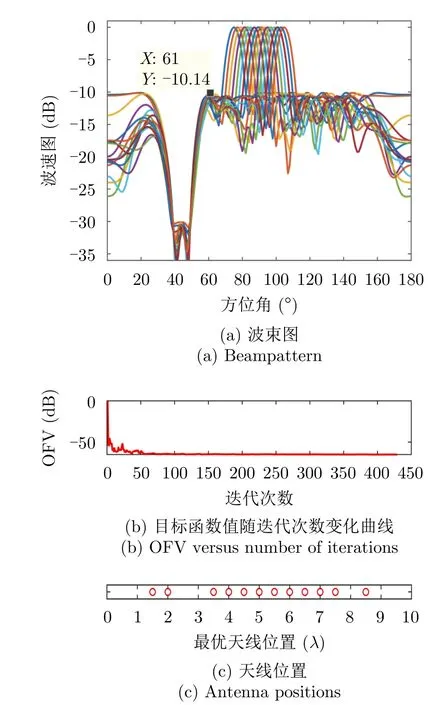
图3 仿真样例2(L =20，=12)Fig.3 Simulation example 2 (L =20，=12)

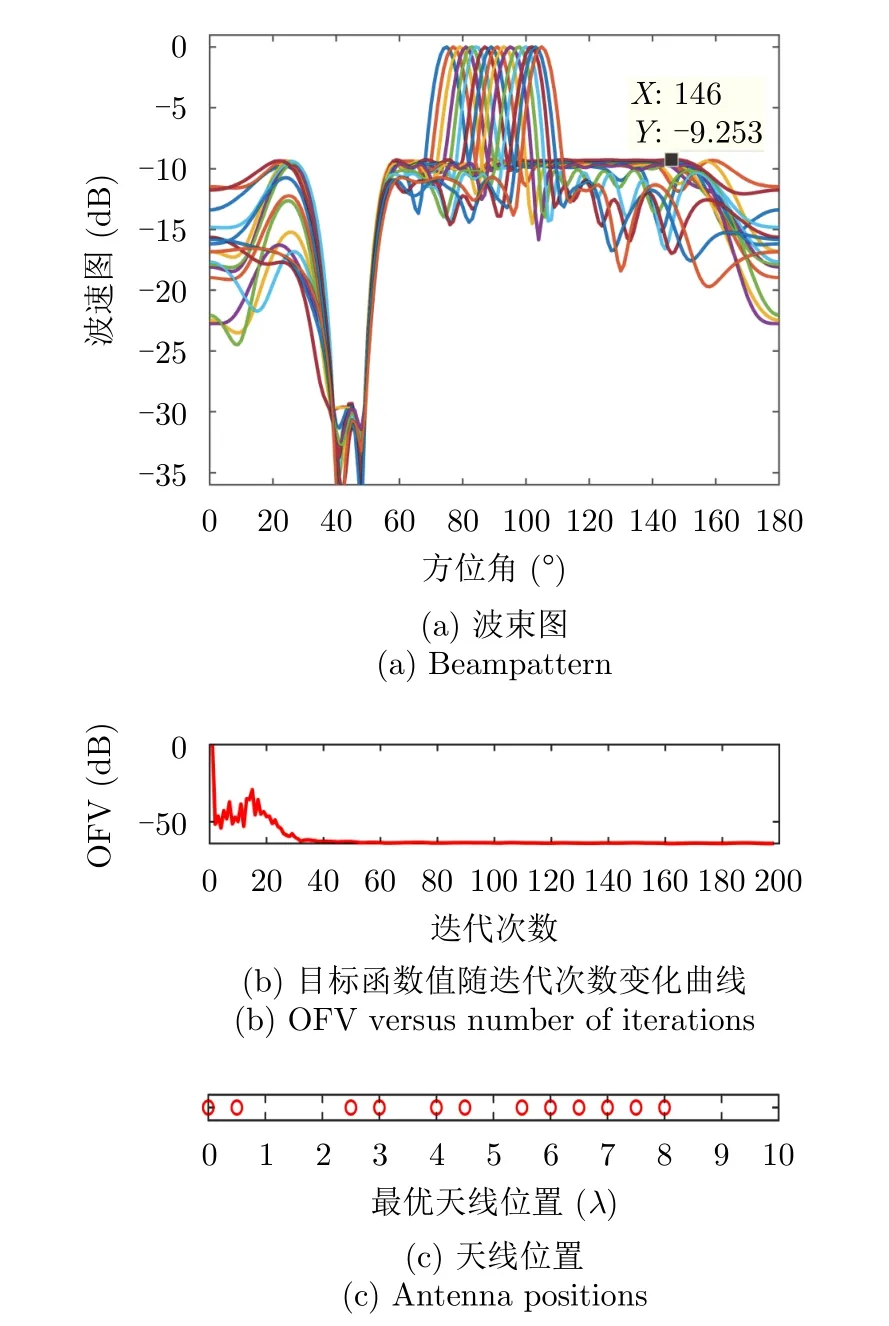
图4 仿真样例2(L =17， =12)Fig.4 Simulation example 2 (L =17，=12)

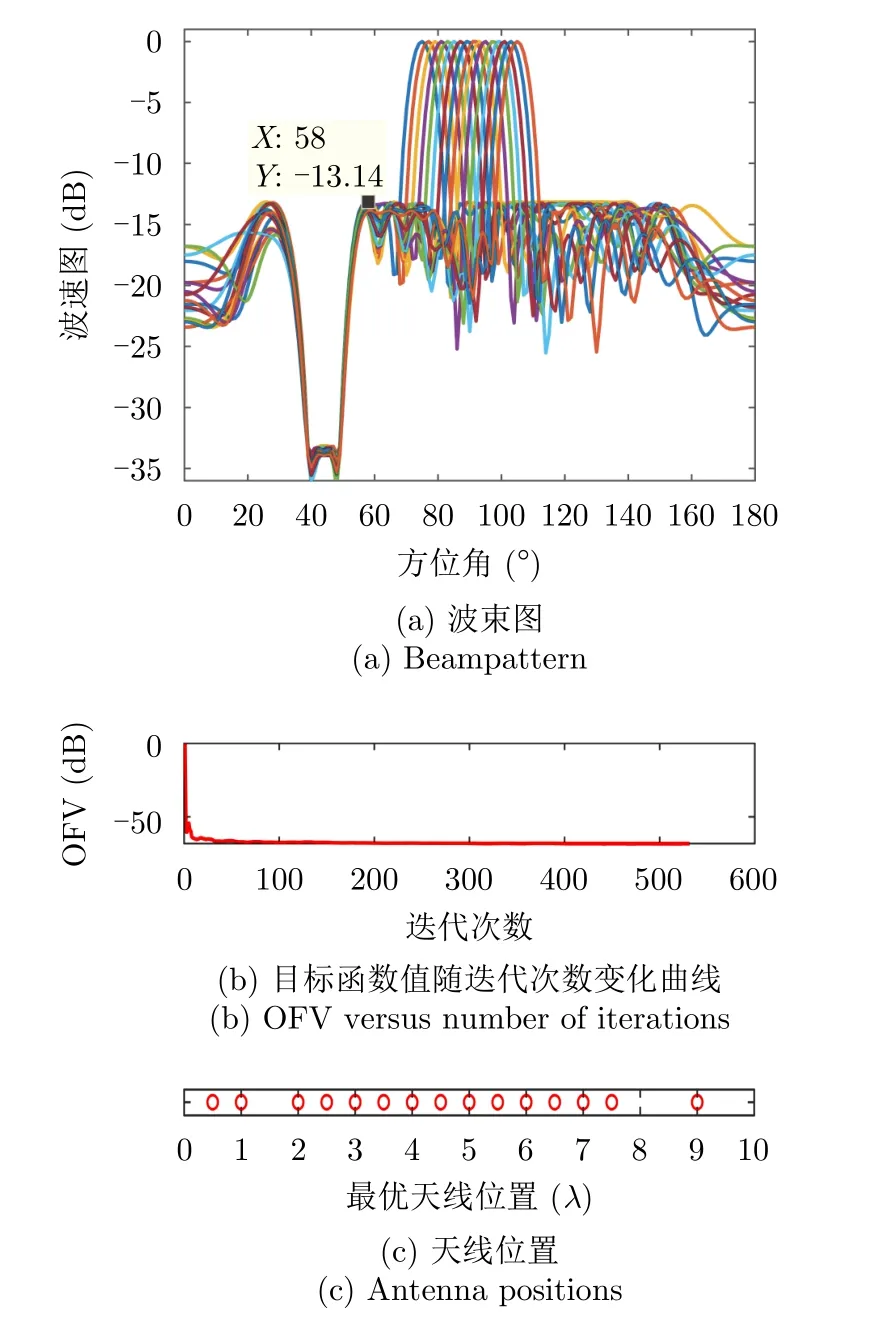
图5 仿真样例2(L =20，=15)Fig.5 Simulation example 2 (L =20，=15)

图6(a)—图6(c)分别给出了仿真样例3的波束图合成结果、优化问题目标函数值(OFV)随算法迭代次数的变化曲线以及最优天线位置结果；从图6(a)可以看到2个波束图具有几乎相同的波束图峰值旁瓣水平，且具有宽波束的波束图主瓣波纹较小，也表明了本文min-max设计准则的有效性；从图6(b)可以看到，经过大约100次迭代后，目标函数值几乎保持不变，算法收敛；从图6(c)可以看到，和样例1和样例2一样，优化后天线单元的位置已经不再是等间距的，具有稀疏结构。

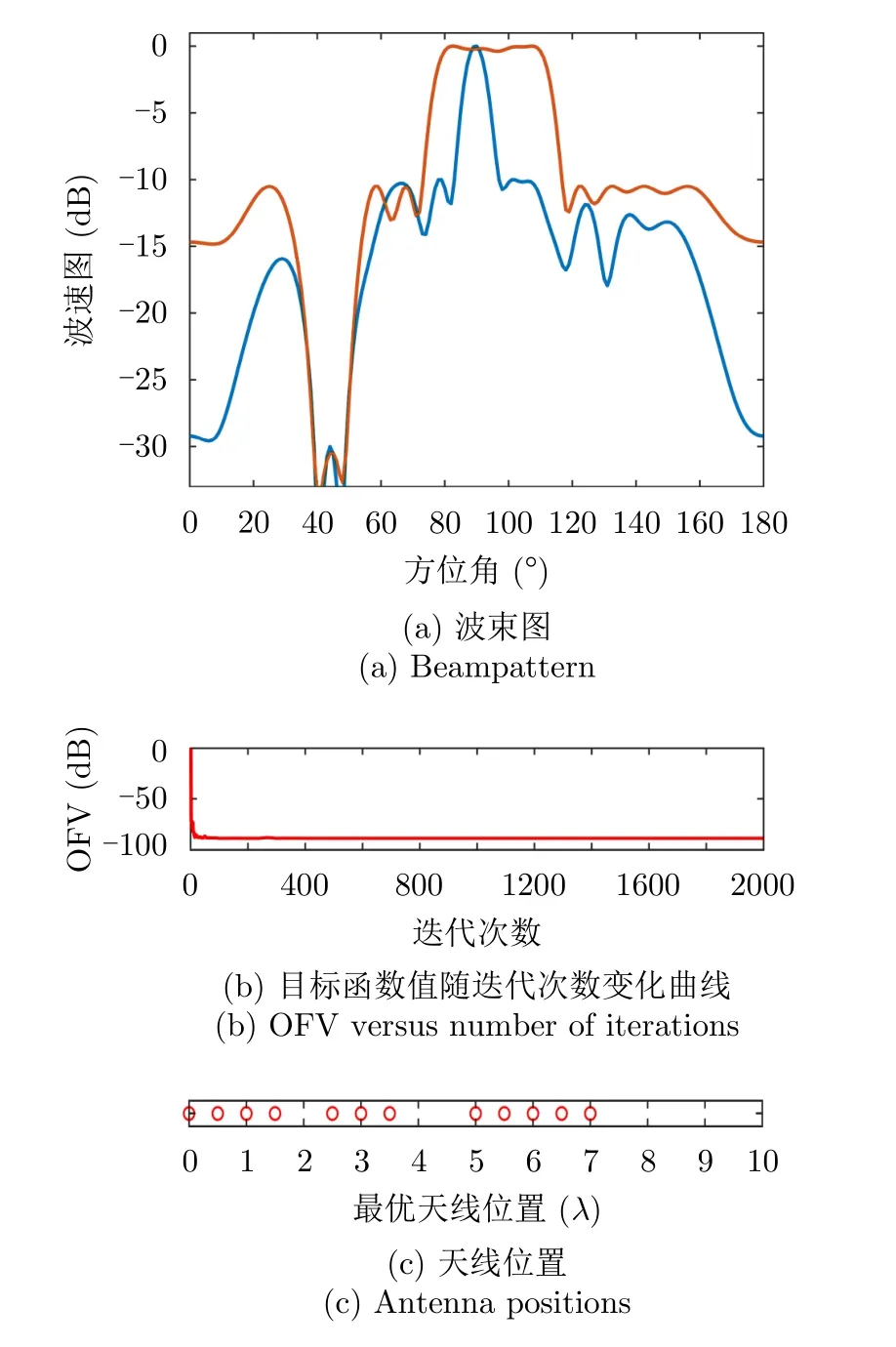
图6 仿真样例3Fig.6 Simulation example 3

样例4：本仿真对比了现有基于ℓp的波束图匹配方法 (ℓ2-NTBF和ℓp-NTBF)[13]，基于半正定二次规划(Semi-definite Quadratic Programming，SQP)的方法[4]求解波形协方差矩阵以及根据此协方差矩阵利用循环算法获得波形(CA-SQP)的方法[18]。本文参数设置为L==16，间距为半波长其余设置为旁瓣Θs。其他参数保持不变。图7绘制了波束图对比结果，从图中可以看出本文方法所合成的波束图旁瓣最低，证明了本文方法的优越性。

图7 不同方法获得的波束图结果Fig.7 Beampattern results obtained by using different method

5 结语

针对现有集中式MIMO雷达的发射波束图合成设计仅考虑均匀线性阵列结构无法用于非均匀布阵，以及现有稀疏结构的MIMO雷达发射波束图设计方法仅考虑在设计中合成一个发射波束图不能满足雷达多波束需求的问题，本文提出了基于minmax准则的集中式MIMO雷达多波束图合成和雷达天线阵元位置优化联合设计方法。为求解非光滑、非凸、大规模优化问题，本文结合Lawson算法、MM和ADMM推导了有效的求解算法。仿真实验表明，本文方法对MIMO雷达多波束设计和天线位置选择的有效性。该方法的提出弥补了现有集中式MIMO雷达天线位置选择方法仅合成一个波束图的不足，通过对集中式MIMO雷达的天线位置和多个波束图(多组探测波形集)同时优化，达到最优天线位置和多波束的能力，为集中式MIMO雷达向工程应用提供了有价值的参考。