基于Dijkstra算法的地震灾害应急避难路径分析*

李文倩，周到洋，郑媛媛

(1.天津城建大学 经济与管理学院，天津 300384；2.天津城建大学 国际教育学院，天津 300384)

0 引言

相比于暴雨、洪水、火灾等自然灾害，地震发生的时间更短、破坏力更强。地球上每年发生的破坏性地震约100次，面对频繁的地震灾害，科学家从未停止探索降低地震灾害所造成的生命财产损失的途径。特别是在突发地震灾害来临时如何最大程度减少损失，已经成为当前城市规划与建设过程的重要命题。

早在20世纪初，科学家就开始针对灾害避难行为规律进行了探索。然而，由于缺乏科学合理的数据调查统计，且有关地震灾害避难行为的研究极少，因此尚未形成完整的理论体系。Dunn和Newton(1992)针对路网通行能力开展研究，为灾害条件下路径的最大流量计算提供了思路。Fredrich等(2000)研究分析了地震发生时的最佳避难疏散路径。Yamada(2000)针对交通分配能力，提出了最短路撤退规划(SEP)方法。而Campos等(2000)提出了“K-最短路径方法”，以连接各个路段的起点和终点，通过计算最大容量和通行时间，确定最优的撤离路径。Cova和Johnson(2003)针对混乱程度高的路网建立了基于车道的网络流实验模型，能够确定复杂路网中的最佳避难路线。

我国洪水、地震灾害频发，有关应急避难场所与避难路径方面的研究起步较早。如何少苓等(1994)针对东平湖蓄滞区内的居民应急避难路径选择，利用动态规划中的最优控制方法，设计了避难最佳路径。万庆和励惠国(1995a，b)针对蓄滞洪区的灾民撤退转移过程进行了定位和定量的空间动态模拟。李发文等(2005)提出了“点、线结合”的应急避难路径规划与动态最佳避难路径的计算方法。于大超等(2016)通过静态与动态最佳路径分析方法，建立了洪灾避难过程的应急避难最佳路径分析模型。黄诗锋等(1998)运用GIS技术对避难者在灾害情景下避难过程道路网络进行动态模拟，提出了最佳动态路径模型。张昊雁和张玉坤(2014)基于GIS空间分析手段，对天津市的防灾避难场所进行了评估。郭鑫等(2017)以疏散距离最短为目标，在不超过容量限制的条件下，确定了天津市中心城区各受灾点到达对应避难场所的最佳路径。陈兴民(2000)针对个体在地震灾害下所具有的各种行为反应，提出了8种应急避难行为类型。苏建锋和张庆斌(2021)利用熵值权重与灰色关联分析相结合的评价模型和GIS空间分析方法，对天津市中心城区地震应急避难场所进行了适宜性评价。陈晨和程林(2021)通过多层回归模型探讨了城市客观建成环境和感知建成环境，研究了居民地震避难行为对安全性和避难效率的影响机理。魏本勇等(2022)构建了基于避难场所容量限制的灾民应急疏散分配与路径选择算法模型，并以北京市为例，对给定情景下的灾民应急疏散路径进行了实证研究。

综上所述，我国有关地震避难规划更注重考虑避难空间和人口规模等问题，而极少考虑居民个体的避难行为特征。针对应急避难的研究多聚焦于避难通道的设置上，而较少研究从静、动态角度出发选择最佳避难路径。针对上述问题，本文开展基于Dijkstra算法的地震灾害应急避难路径分析，以天津市长虹公园为地震避难安置点，分别采用静态与动态Dijkstra算法开展地震应急最佳避难路径研究。

1 天津地区地震分布

1.1 自然地理概况

天津市地处华北平原北部沉降带上，毗邻渤海海域，地震活动的发生与地质构造特点密切相关。天津市市区内有沧东、白塘口西、蓟运河、海河等4条主要断裂带穿过，其持续性活动极易引发地震。城市表层土质以松散的淤泥为主，地基地震效应明显，使得地表建筑物对地震激励较为敏感，极易遭到地震破坏。

1.2 地震分布特征

天津地区地震活动频繁，≥4.0地震平均每10 a发生1次。根据天津市地震局公开数据，天津地区2021年7～11月小震及6～8级历史大震分布如图1所示。

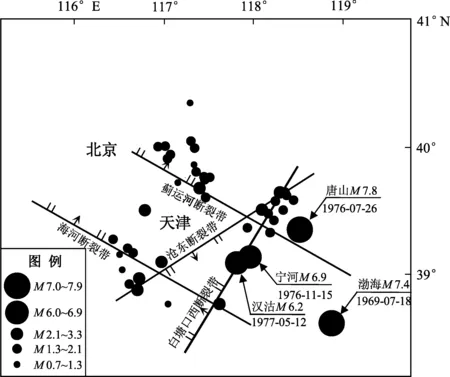
图1 天津地区2021年7—11月小震及6～8级历史地震分布图

由图1可以看出在短短5个月内，天津地区发生不同震级地震共计48次，大部分分布在武清、静海、宝坻和蓟州等，虽然震级均在3.3级以下，但非常频繁。而从历史地震分布情况来看，20世纪60年代至70年代，天津周边地区地震较为频繁，包括1969年渤海7.4级地震、1976年宁河6.9级地震、1977年汉沽6.2级地震与1976年唐山7.8级地震等，主要集中在渤海周边区域。已有研究结果显示(赵宏维，1993)，天津地区地震活动受1965年山西垣曲5.5级强震的影响，华北地块内沿西南到东北对角线方向分布的一条活动带正好通过天津，该最大破裂方向可能指向下次大地震发生的方位。

2 地震应急避难行为规律分析

2.1 心理特点

避难心理是指在地震灾害发生时，人们在应急情况下的心理反应，它直接影响人们的避难行为及对避难路径和避难场所的选择。地震灾害具有突发性和多变性，常常瞬间爆发并威胁人的生命。当灾害强度超出人的心理承受能力时，会引发心理的极度恐慌。过度的恐慌会导致人们反应迟钝、行为受阻，甚至出现采取极端行动或拒绝逃生等异常情况。地震发生后，人们的紧急避难心理特点见表1(冉茂梅，2012)。

表1 紧急避难心理特点

2.2 行为特性

面对地震灾害，人们会因种种主观和客观的原因，采取不同的避难行为。在地震灾害突然发生时，人的避难行为会经历两个过程：一是对灾害瞬间认知判断的心理过程，人们通常会以避难距离最短或时间最短为标准，作为避难路径和避难场所选择的依据；二是受避难心理支配，采取不同避难行为方式的行动过程。地震发生时，人们原本的平静心理会受到本能需求驱使产生焦虑惊恐的情绪，甚至有人会出现意识模糊、思维混乱、行为失态等种种异常情况。灾害中由于过分的突发刺激，人们会惊愕、头脑空白，可能失去应对灾害的能力，无法进行正常的避难活动。

2.3 行为规律分析

依据不同的心理所表现出的避难行为存在明显差异：积极的避难行为可以帮助人们做出正确的避难决策，而消极的避难行为则影响着人们对应急避难路径的选择。消极避难行为主要包括以下行为(王滢，2016；王江波，苟爱萍，2016)：

(1)瓶颈口竞争行为。灾害情景下，避难者可能因失去理性而导致行为混乱，造成交通堵塞、道路破坏等情况，甚至会使道路变窄从而出现瓶颈口。在恐慌心理的驱使下，人们会试图迅速通过瓶颈口以抵达避难场所，因此，极易造成瓶颈口地区及避难路径上的竞争行为。

(2)延缓择机行为。由于受到自身避难经历、避难知识掌握程度等因素的影响，部分人会因为对地震灾害的严重性不够重视，不了解其造成的破坏，盲目乐观，耽误了采取避难行为的最佳时机。

(3)从众结伴行为。由于逃生路线不明、决策困难、对地震灾害恐慌等原因，人们容易失去主见而出现盲从现象。在灾害发生后，并非全部人员都能选择正确的避难路径和避难场所，若缺乏理性的思考，盲目从众，将会错失避难最佳时机。

上述消极行为会直接影响避难结果，因此在进行应急避难路径的分析选择时，应考虑消极行为对避难行为产生的影响，以保证应急避难最佳路径选择的合理性与准确性。

3 基于Dijkstra算法的最佳应急避难路径研究

本文选取天津市某居民小区为研究对象，该居民点位于芥园西道与密云路交叉口处，现有住户989户，居民数约4 500人。根据天津市避难规划，该居民小区以长虹公园作为灾害避难场所。该公园地质条件良好，旁边无高压输变电线路和高层建筑物，周边道路有红旗路、黄河道、长江道等主干道路，道路安全畅通、交通便利。长虹公园应急避难场所占地面积32.4万m，绿地面积22万m，紧急情况下可容纳10万人临时避难。同时配备综合性设施，可安置受助人员30 d以上，属于Ⅰ类地震应急避难场所。

由于地震具有突发性大、破坏性强等特点，其造成的建筑物与道路交通破坏情况从理论上难以评估。因此，本文假设地震已发生或预测会发生在所研究居民小区及周边范围，且主要交通道路尚未破坏并基本处于畅通状态，以此研究地震灾害下的应急避难路径。最佳避难路径是指在选定范围的道路网中，从起始地点到目的地点的以距离或时间为权重的连续性最短路径(王江波等，2014)。本文所研究居民点(设居民小区为起始地点)到安置点(设长虹公园为目的地点)的道路网简化图如图2所示。最佳避难路径可保证在地震来临时，以最快的速度转移人口、财产等，从而最大程度减小灾害损失。本文考虑距离最短与时间最短两种情况，距离最短路径属于静态路径，与实时交通状况无关，只与交通道路网的分布相关；时间最短路径属于动态路径，不仅与交通布置相关，还与实时交通状况有关，需建立合适的路权模型进行分析。

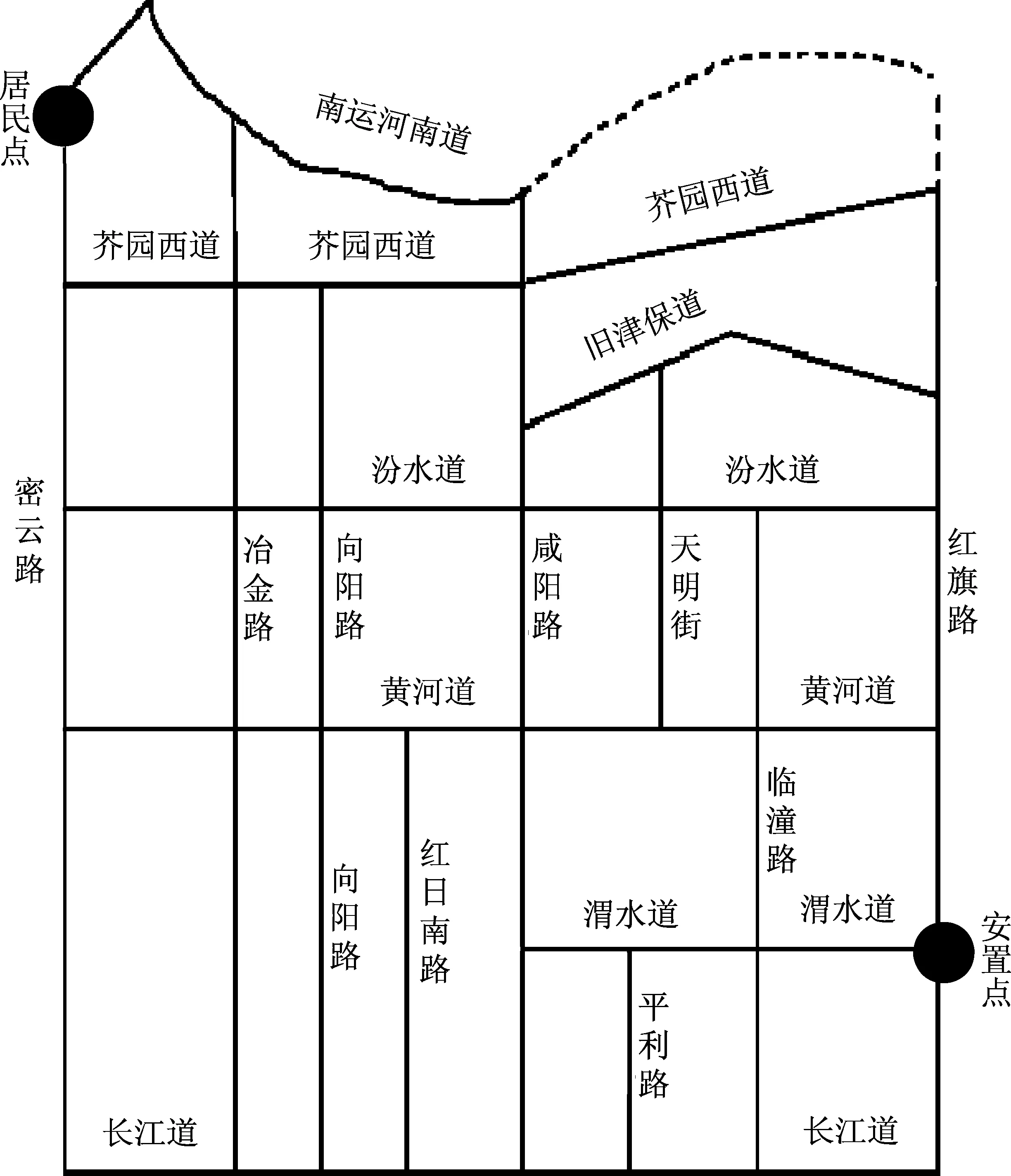
图2 居民点到安置点道路网简化图

3.1 基于静态Dijkstra算法的应急避难路径选择

3.1.1 静态Dijkstra算法

静态Dijkstra算法适用于所有弧的权重为非负的最短路径计算，可计算给定节点到途中其他节点的最短路径。其基本思想是得到标记初始点到某个节点的最短路径，再依次寻找到下一个节点的最短路径，以此类推直至目标节点。其主要特点是以起始地点为中心向外层扩展，直到扩展到目的地点为止，如图3所示。

由图3可知，～为道路网中的节点，～为节点间的路权。采用静态Dijkstra算法是从起点开始，依次计算从到道路网中各节点、、、的最短路径，进而逐步推出到终点的最短路径，算法过程可直接在道路网中逐步标号完成。如果已经得到至的最短路径，即可在点上标号为[，]。第一个标号代表点至点的最短路径的长度，第二个标号代表点至点的最短路径中之前的节点，那么表示已经得到至的最短路径，且最短路径是，最短路径可以根据第二个标号反向追踪而得到。

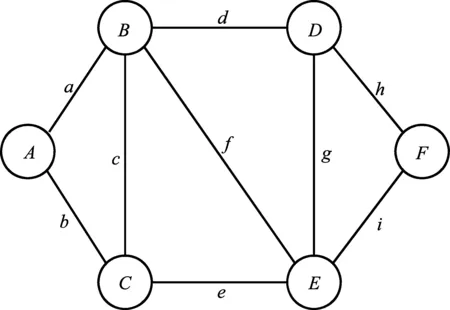
图3 静态Dijkstra算法的路网示意图

3.1.2 距离最短的应急避难路径选取

根据图2选取道路各路段距离为静态Dijkstra算法的计算权重，从居民点出发到安置点的道路网络图及各路段权重如图4所示。由图可知，寻找最佳应急避难路径，实际上是基于最短路径长度条件，找出从居民点到安置点的最短距离。根据静态Dijkstra算法最短路径的计算思想及各段道路长度，计算节点～间的相邻最小距离并标号。

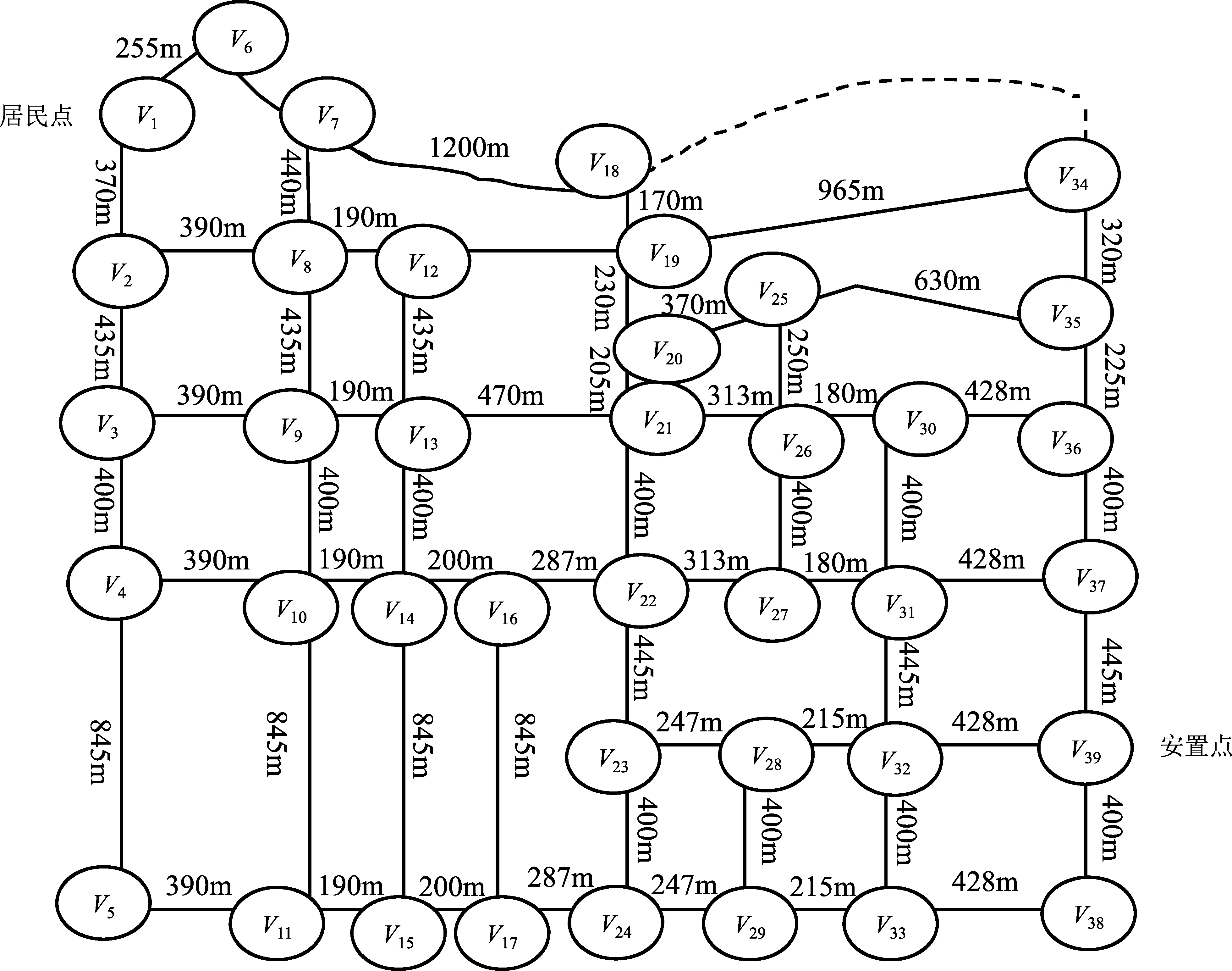
图4 居民点到安置点的道路网络图及各路段权重图

例如，给标号[0，1]，从居民点开始可有两条路径，即分别向与前进，因此可对与进行标号并计算最短路径：

对于密云路(，)、南运河南道(，)，计算：

“min= {0+370，0+255}=255”，给标号[255，1]。

对于密云路(，)、南运河南道(，)，计算：

“min= {0+370，255+300}=370”，给标号[370，1]。

对于密云路(，)，计算：

“min= {370+435}=805”，给标号[805，2]。

根据上述静态方法类推，即可对每个节点进行标号，获得最终到达安置点处的最佳路径，即：

渭水道(，)、红旗路(，)、红旗路(，)，计算：

“min= {3 005+428，3 019+445，3 833+400}=3 433”，给标号[3 433，32]。

由反向追踪得：

→→→→→→→或，→→→，→或，→→，→→

即得到的最短路径为：→→或，→，→，→，→，→，→→→→→→→

由上可以确定最短路径长度为3 433 m，路网中最短避难路径示意图如图5所示。由静态Dijkstra算法计算得到的所研究居民小区居民距离最短应急避难路径如图6所示。

图5 路网中的最短避难路径示意图

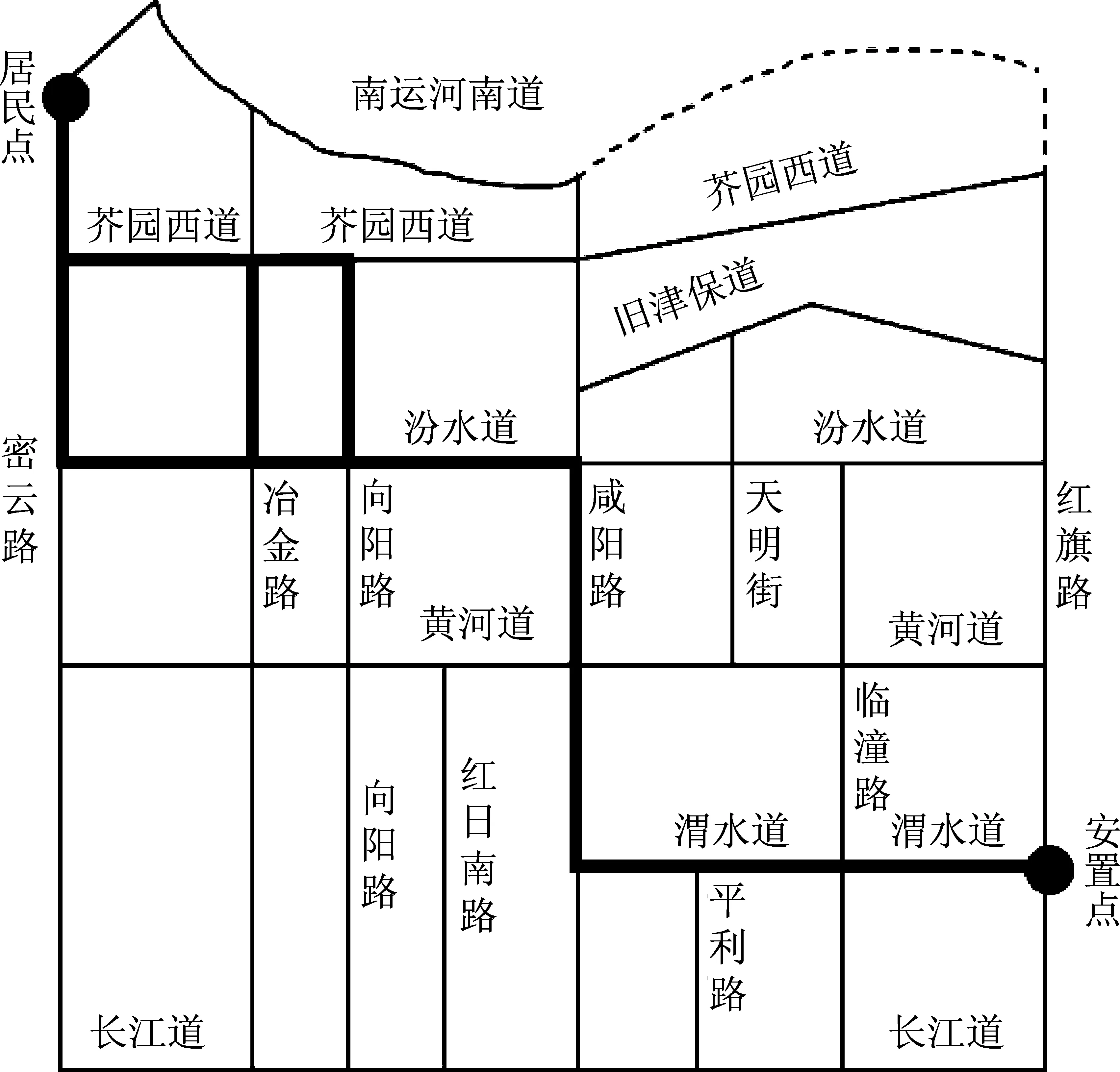
图6 基于静态Dijkstra算法计算最佳避难路径示意图

3.2 基于动态Dijkstra算法的应急避难路径选择

3.2.1 动态Dijkstra算法

基于动态Dijkstra算法获得避难最佳路径，主要是通过动态路径分析计算居民从居民点到安置点撤离过程中所消耗的时间得到。整个撤离过程所消耗的时间可以分为两部分来计算：一部分为居民、车辆及财产物资在转移道路上所经历的时间；另一部分为人员、车辆在道路交叉路口转移等待延误的时间。

动态路径分析在路权分析的基础上进行。路权是指通过某一路段的行驶或撤离所消耗的时间，通常用路阻函数来表示，其可表征路段行驶时间与路段上的交通负荷之间的函数关系。

因此，根据动态Dijkstra算法计算避难时间，可基于道路网络图，设点到点为路段[，]，(，)为路段[，]的路权，则有(杨茜，贾艾晨，2011)：

(,)=(,)+(,)

(1)

式中：(，)为通过路段[，]所花费的时间；(，)为通过路段[，]的平均延误时间，单位是min。

依据1964年美国联邦公路局提出的路段特性函数BRP模型，通过路段[，]所花费的时间(，)的计算公式如下(张伟，2011)：

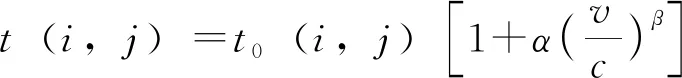
(2)

式中：(，)为零流量阻抗，即交通量为零时自由通行所花费的时间；为路段[，]的通行车辆数目；为路段[，]的实际运输能力，单位为辆；，为阻滞系数，=15，=4。

当路段[，]交通量为零时，车辆自由通行该路段所需时间(，)为：

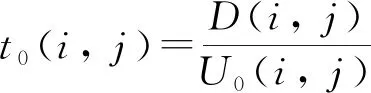
(3)

式中：(，)为路段[，]的长度距离；(，)为路段[，]交通量为零的通行速度。(，)计算公式如下(城市道路设计规范，CJJ 37—90；城市道路工程设计规范，CJJ 37—2012)：

(,)=

(4)

式中：为混合交通状况的影响折减系数，当路段上机动车道与非机动车道之间有分隔带时=1，没有分隔带时=08；为路段[，]宽度的影响系数，具体取值见表2(王炜等，2019)；为路段[，]的设计车速。

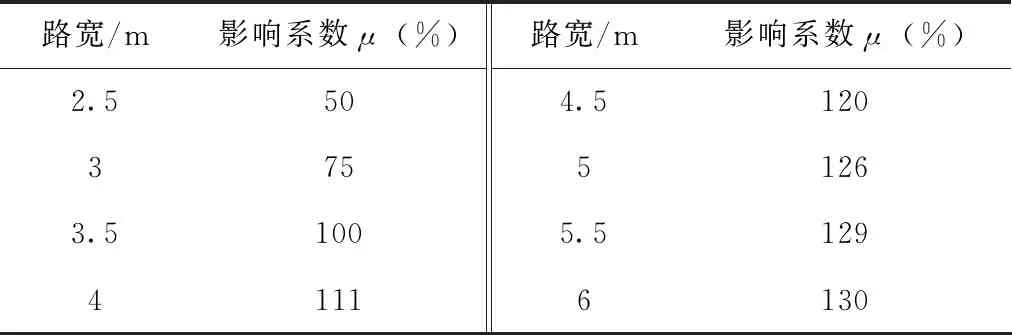
表2 道路宽度与影响系数之间关系

通过路段[，]的平均延误时间(，)的计算公式为：

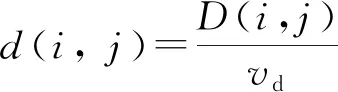
(5)

式中：为路段[，]的通行速度。

3.2.2 时间最短的应急避难路径选取

(1)最短路径数学模型

假设=<，>是一个非空的简单有限图，作为结点集，作为边集。对于任何=(,)∈，()=(,)权值。是中的两点间的一条有向路径，定义的权值()=∑()，则最优解中两点间权最小的有向路径就成为这两点间的最佳路径。最佳路径的数学计算模型为：

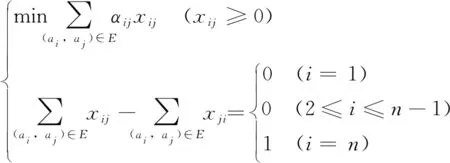
(6)

式中：为(，)在有限路径中所出现的次数。

(2)路段随机度模型

在正常行驶情况下，道路上两车辆间的车头时距越大，两车间的相互干扰程度越小，则两辆车自由行驶程度越大。因而可利用随机度来表征道路上某车辆自由行驶的程度，计算公式如下：

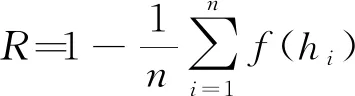
(7)

式中：为车流行驶的随机度；为道路上总的车辆数；()为车辆的影响函数。

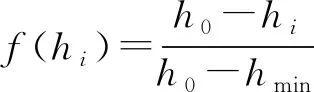
(8)

式中：为两车辆间的车头时距；为车辆之间互不影响的车头时距阈值；为车辆之间保持安全行驶所必需的车头时距阈值。有关领域专家对该模型的实测数据整理得到与的关系推荐见表3。

表3 车头时距阈值推荐值

据车头时距的实际情况，计算出车流行驶的随机度，按照道路所受到的交通条件将避难路径划分为3个等级，分别为轻警、中警和重警，各个等级的表示含义如下：

轻警：0.6≤≤1，表示避难人员及车辆在撤离过程中几乎不受交通条件限制，处于稳定状态，可以合理地选择避难路径到达安全的安置点。

中警：0.2≤≤0.6，表示避难人员及车辆在撤离过程中受到交通条件限制，处于不稳定的状态，此时的道路基本处在饱和状态，要做好分流准备。

重警：0≤≤0.2，表示避难人员及车辆在撤离过程中受阻，出现排队、阻塞现象，此时必须进行相应的分流工作，以保证撤离工作顺利完成。

由上可知，表征该道路内避难人员及车辆在撤退过程中受到交通条件所限制的情况。越大说明所受交通条件限制越弱，在轻警和中警情况下，可以说明避难道路路径通行的总人口基本不会超过各道路最大通行量，选择这样的路径避难会更为顺利。越小说明交通条件限制越强，在重警情况下，该路段更容易受到人们消极避难行为影响而产生避难交通不畅。

3.2.3 时间最短路径方案的确定

本文在建立目标函数时遵循以下设计原则：①模型的目标为追求路径距离最短；②在距离最短路径里选取时间最短路径；③保证避难场所分配的总人口不超过已知最大设计容量；④保证避难道路路径通行的总人口不超过各道路最大通行量。

基于上述设计原则，经过实地调研统计数据，本文所研究的天津市某居民小区居民撤离到应急避难场所的居民人数约4 500人，未超过长虹公园避难场所的最大设计容量。依据上述动态Dijkstra算法的路阻函数进行计算，以避难撤离时间最短为原则选取最佳避难路径，得到避难路径各路段的路权和随机度，见表4。

由表4可知，经过随机度检验，路段-、-、-、-、-、-、-的随机度大于06，为轻警状态，人员车辆可正常通过这些路段，不受到交通条件的影响限制。路段-、-、-、-、-、-、-随机度范围为052～060，为中警状态。综合考虑所研究居民小区避难居民数量较少且计算所得随机度最小值为052，较为接近轻警状态，基本能够满足避难道路路径通行的总人口基本不会超过各道路最大通行量的条件，在避难过程中可不采取分流措施。

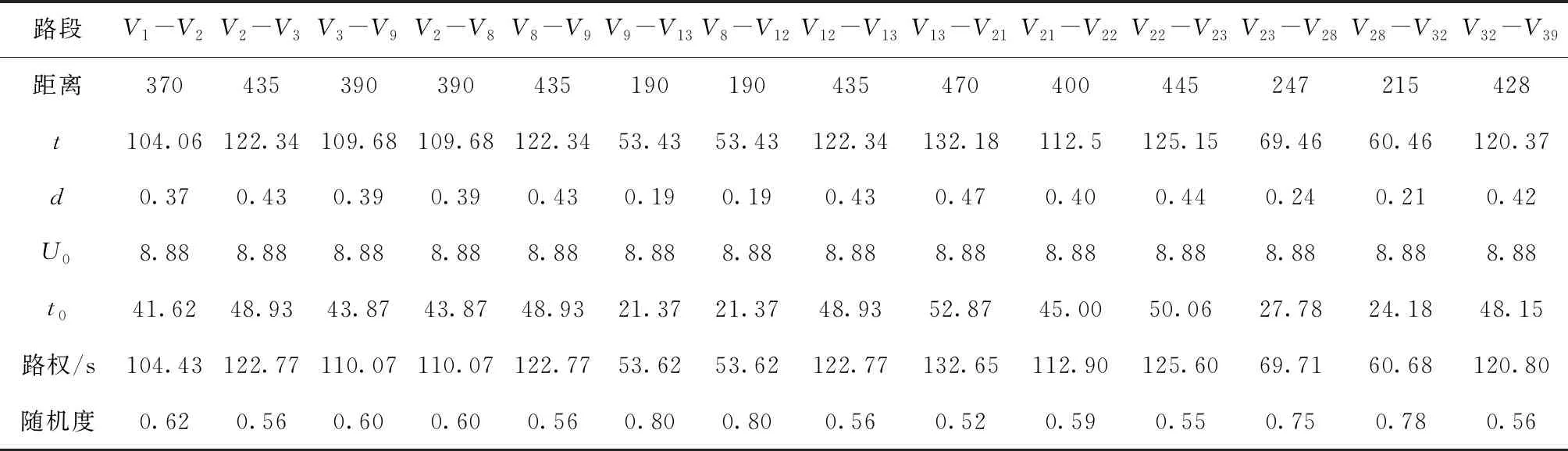
表4 基于动态Dijkstra算法的路权与随机度计算结果

根据上述计算结果可知，地震灾害下从居民小区到安置点长虹公园避难场所的时间最短的避难路径为：→→或，→，→，→，→，→，→→→→→→→，居民点到安置点的避难撤离最短耗时为18.93 min，使用动态Dijkstra算法计算得到时间最短的避难路径与使用静态Dijkstra算法计算得到的距离最短避难路径保持一致。基于动态Dijkstra算法计算获得的最佳避难路径如图7所示。

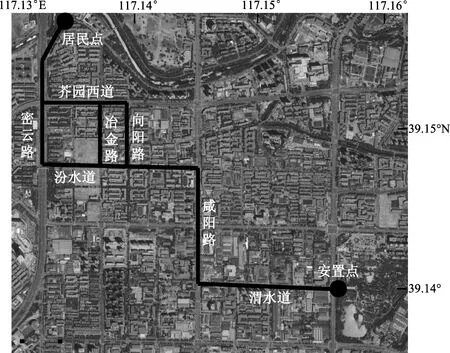
图7 基于动态Dijkstra算法计算最佳避难路径示意图

4 结论

本文考虑地震灾害下人的避难心理、行为特征、行为规律等，以天津市某居民小区及其避难场所长虹公园为研究对象，使用静态与动态Dijkstra算法开展最佳应急避难路径研究，获得主要结论如下：

(1)根据天津市某居民小区到达长虹公园的道路网络图，采用静态Dijkstra算法计算获得居民点到安置点距离最短的应急避难路径，最短路径长度为3 433 m。

(2)通过对灾区道路的动态路径分析，采用动态Dijkstra算法计算用时最短的应急避难路径，得到由居民点到安置点的最短耗时为18.93 min，最佳路径与通过静态Dijkstra算法的计算结果一致。

(3)在面临地震等突发性紧急情况时，使用Dijkstra算法可准确、有效地计算获得最佳应急避难路径，为城市灾害避难路径选择与应急预案制定提供了方法基础与应用依据。