基于高维特征聚类优化的随机森林算法研究7

*王 博，庄暨军，熊 军，罗小臣

（1. 井冈山大学电子与信息工程学院，江西，吉安 343009；2. 井冈山大学学报编辑部，江西，吉安 343009；3. 井冈山大学计财处，江西，吉安 343009；4. 井冈山大学图书馆，江西，吉安 343009）

0 引言

随机森林算法（RF）算法是集成学习（Ensemble Learning）算法中的典型代表之一。算法基于统计学习理论，采用自助重采样技术（Bootstrap Sampling）

从训练样本中抽取多个样本集，利用抽取的样本集分别构建决策树模型，然后将若干个决策树聚集在一起，通过多数投票或取平均得到最终结果。决策树算法与集成学习思想是构建RF 算法的基石。

随机森林算法具有能容忍高数据噪音，同时也具有高预测精度，而被众多学者广泛运用到社会中各个领域。比如文献[1]中，Chai.Z 将随机森林算法运用到工业故障分类，提高了故障检测精度；文献[2]中，Cheng.Li 在交通运输领域中运用随机森林算法，极大提升了运输效率和承载率；ZAFARI.A 在文献[3]中的评估管理领域运用随机森林算法，得到了更加准确的评估预测结果。但即便如此，随机森林算法仍然存在自身的缺陷：在对高维度特征进行筛选和选取的有效率比较低、对动态数据聚类的泛化误差估值较大。针对这些缺陷，国内外学者对随机森林算法做了许多改进优化的研究。在文献[4]中，王德军等将基于时间序列数据对随机森林分类算法优化，结果提高了10%的分类精度；文献[5]中，刘曙光等提出的多时相遥感数据结合随机森林特征变量优化方法，将总体分类精度提高了近9%；王磊等在文献[6]中采用聚类欠采样加权随机森林算法，提高了预测精度。以上的算法优化对提高随机森林算法的预测精度和分类精度都取得了很大进展，但是在对高维数据划分特征度量时如何提高聚类性能，目前研究比较欠缺。

特征选择是从原始特征集中抽取部分特征，使其能达到降低特征维度提高算法性能的效果。算法在构建决策树时，会随机的抽取部分特征，利用特征评估方法选出其中分类效果最好，即最重要的特征作为分裂特征，这为随机森林进行特征选择奠定了理论基础。但由于随机森林算法在构建过程中引入了特征随机选择策略，所以单纯的根据特征在决策树节点被选为分裂特征的次数来判断特征是否重要的方法是不可取的。Breiman 在对随机森林进行系统的分析后，提出使用袋外数据内部估计方法监测随机森林的误差，并将其作为随机森林度量特征重要性的依据。

现尝试用一种高维聚类优化算法，针对高维特征数据集，采用K 均值聚类和模糊C 均值聚类相结合的方法，对数据集的高维特征聚类，传统随机森林算法进行优化，通过计算DBI、根据相关性阈值排序，筛选出高维特征簇群，以达到提高高维特征数据集聚类效果的目的。实验结果证明，该方法是切实有效的。

1 传统随机森林算法

传统随机森林算法中，对高维数据特征度量时运用的方法主要是随机置换法。即在首先对高维数据的所有相关特征进行随机置换，置换后再进行迭代测试，根据测试结果的误差变化越大，则代表该特征的相关程度越高。

从以上步骤可以看出，随着训练数据集的不断增加，高维数据特征需要的训练时间、空间性能呈指数级增加，最终将造成训练速度缓慢、训练效果降低的后果。本文将采取高维聚类的方法，对传统算法加以优化，以提高传统随机森林算法在高维数据训练方面的性能。

2 基于高维聚类优化的随机森林算法

2.1 聚类方法介绍

本文采用KM 聚类（K 均值聚类）、FCM 聚类（模糊C-均值）两种聚类方法相结合，根据样本相似度划分族群，对高维数据集特征进行聚类。根据这两种聚类算法得到的DBI（聚类有效性）值，取DBI 最小值为最佳类数。

2.1.1 KM 聚类

根据文献[9]的研究，当DBI 的值与聚类效果成正比，所以，当DBI 值最小时，表示此时的聚类类数为最佳值。

2.2 HDFC-RF 算法

2.2.1 HDFC-RF 特征评估算法

2.2.2 HDFC-RF 算法流程图

根据上述的介绍，将HDFC-RF 算法流程归纳如下：

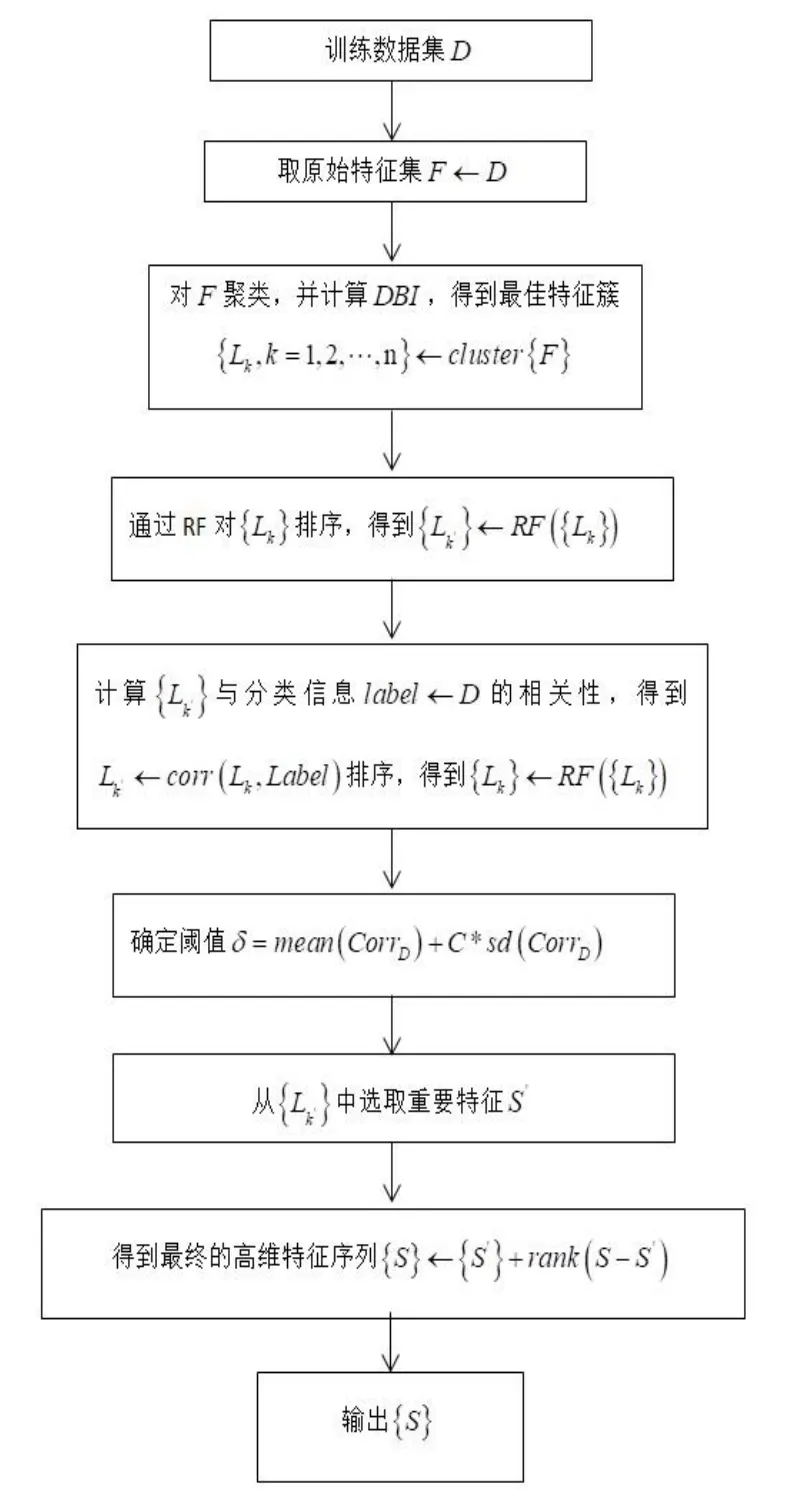
图1 HDFC-RF 算法流程图Fig.1 HDFC-RF algorithm flow chart

将文献[10]和文献[11]中的高维数据集Colon Tumor 作为输入数据集。Colon Tumor 属于生物数据集，在同等样本规模下，具有更高维的数据特征，符合本文HDFC-RF 算法对高维数据特征聚类的训练数据集要求。

表1 实验数据集Table 1 Experimental data set

3 实验分析

3.1 实验准备

3.2 实验结果

将本文的HDFC-RF 算法与传统的RF 算法、文献[6]中的FSRF 算法进行比较，为了得到更稳定的结果，将三种算法运行30 次的均值作为最终结果。实验结果对比如图2、图3 所示：

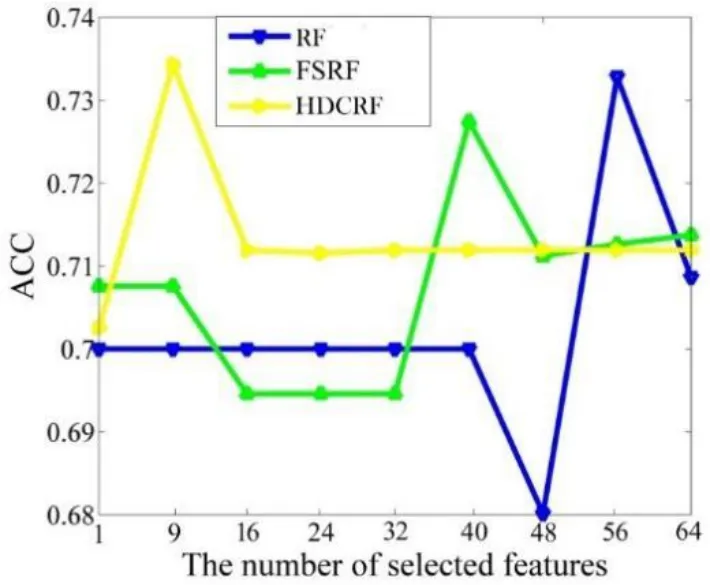
图2 HDFC-RF、FSRF、RF 聚类效果对比Fig.2 Training effect comparison of HDFC-RF&FSRF&RF

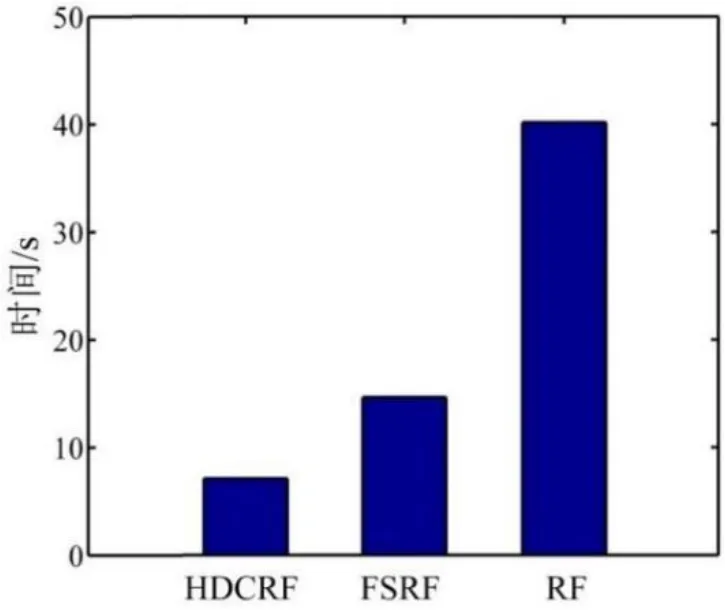
图.3 HDFC-RF、FSRF、RF 训练时间对比Fig.3 Training Time comparison of HDFC-RF&FSRF&RF

根据以上两图可以得到如下结论：

1）图2 表明，在数据集训练中，HDFC-RF 算法在重要特征集的前10 个特征就达到了最佳的分类效果，而传统的RF 算法和FSRF 算法则分别需要近40 和60 个特征。可见同等样本数的情况下，HDFC-RF 能达到更好的聚类效果。

2）图3 表明，在数据集训练的时间上，HDFC-RF 训练时间为8 s，而FSRF 和RF 算法分别为15 s 和40 s，显然HDFC-RF 训练所需的时间比FSRF、RF 都要明显缩短，速度得到了提高，说明HDFC-RF 算法具有更加高效的训练效率。

4 结论

针对传统的随机森林算法在对高维特征数据集计算速度慢、聚类效果不佳的缺陷，提出了一种基于高维特征聚类的随机森林算法（HDFC-RF），即在提取高维特征数据集聚类时，采用K 均值聚类和模糊C-均值结合的算法，通过计算DBI 指标和对高维特征簇排序后，与相关性阈值δ比较，得到最终的高维特征序列。实验结果表明，经过本文HDFC-RF 优化后的随机森林算法，具有更好的聚类效果、训练速度也更快，具备良好的可行性。