基于最小方差Delta的沪铜期货期权对冲效果回测

浦江燕，王艺天，周子凯

（1.上海立信会计金融学院金融学院，上海201209；2.上海财经大学金融学院，上海201901；3.中国人民银行寻甸县支行国库会计发行部，云南昆明 655200）

一、引言

1973年4月26日，芝加哥期权交易所（Chicago Board Options Exchange，CBOE）正式成立。在此之前，期权在美国只是少数交易商之间的场外买卖。CBOE 建立了期权交易市场，推出标准化合约，标志着期权交易进入了标准化、规范化的全新发展阶段，使期权交易产生革命性的变化。2015年2月9日，我国第一个股票期权产品——上证50ETF 期权在上海证券交易所上市。七年来，我国期权的品种日渐增多，市场规模逐步扩大，为我国投资者提供了许多可用于投资、对冲的金融工具。

铜是一种重要的工业用金属，中国经济的高速发展也和铜金属紧密相连。2018年9月21日，中国第一个工业品期权——沪铜期货期权在上海期货交易所上市。目前，沪铜期货已具一定程度的规模，沪铜期货的价格已经成为国内金属铜的权威报价，甚至在国际上也有了一定的影响力，沪铜期货以及以其为标的的沪铜期货期权日益受到企业和投资者的重视。

期权虽然给投资者提供了更多的投资选择，但由于其杠杆性也会带来更大的风险，所以期权的风险管理十分重要。期权希腊字母是期权风险管理中的重要指标，指的是期权价格关于其各个影响因素的偏导。标的资产的价格是期权价格的风险源之一，Delta 指的是期权价格关于标的资产价格的一阶偏导，也是希腊字母中最为重要的一个，在期权风险管理中，往往会将组合的Delta 对冲至0，即称为Delta 中性策略。

标准化的期权产品面世以后，如何为其合理定价成为人们关注的问题。Black 和Scholes（1973）、Merton（1973）分别提出了无分红欧式期权的定价，为期权定价的研究打下了坚实的基础，在其研究成果基础上形成了Black-Scholes-Merton 期权定价模型（简称BSM 模型）。BSM 模型的提出解决了困扰人们已久的期权定价问题，市场的需要性使得这一模型很快得到大众的接受，迅速广泛地使用起来。

关于BSM 模型下的经典Delta 中性策略，不少学者进行了实证研究。郑浩（2003）比较了中国股指期权Delta 动态对冲和Delta-Gamma 套期保值的效果。魏洁（2011）构造了沪深300 股指期货和期权的组合，用指数期货实现Delta 动态对冲，保持期权的风险在可控范围之内。浦江燕等（2017）以上证50ETF 作为标的进行研究，提出当其价格超过一定幅度，再进行Delta 对冲的方法。熊熊和刘勇（2017）考虑固定时点的Delta 中性对冲策略、Delta 区间对冲策略以及固定历史波动率变化区间Delta 对冲策略,比较上证50ETF 期权及其标的资产上证50ETF 基金套期保值的效果。郭江娇（2020）通过构建基于 Delta 中性和结构化复制期权理论的套保策略，并利用模拟价格路径和真实交易数据进行套期保值操作，证明了该策略在我国铜商品市场的适用性。胡姜等（2021）通过二叉树模型和蒙特卡罗模型分别对我国豆粕期货看跌期权和看涨期权进行实证分析，得到对于看跌期权，都是较小的可容忍区间的对冲后的 Delta 均值和方差最小。对于看涨期权，都是较大的可容忍区间的对冲后的 Delta 均值最小。以上学者考虑的都是基于经典的BSM 模型（假定波动率是常数）下的Delta 中性套期保值策略及其改进。

BSM 模型在广泛使用的同时，缺陷也日益显现。其中最为显著的便是BSM 模型中的分布假设——假设股票价格服从几何布朗运动。这个假设也意味着，市场中标的资产价格的对数收益率的波动率是常数，但是这个假设与现实情况显然具有较大差异。

由于BSM 模型条件的限制，期权定价相关的理论如期权希腊字母对冲策略也存在缺陷。因此，学者们对希腊字母对冲Delta 调整进行了改进，主要包括如下两个方面：（1）对BSM 模型的改进，主要有随机波动率模型和局部波动率模型；（2）对原有模型求出来的希腊字母加以调整，最为典型的是Hull 和White（2017）在局部波动率模型的启发下，提出了依据过去市场数据构建二次模型，将常规Delta 调整为最小方差Delta（MV Delta）的改善方法。针对Delta 调整方法的改进，王清水（2019）对台指期权作了实证研究，比较了不同改进策略套期保值的效果。刘宝杰（2020）使用人工神经网络模型探寻标的资产价格的变化与资产的波动率变化之间的关系，并使用上证50ETF 期权的日度交易数据进行了最小方差Delta 的实证研究。

本文选用上海期货交易所沪铜期货期权作为研究对象，研究不同Delta 策略套期保值的效果，分别使用（1）每日调整头寸的BSM Delta 对冲；（2）每日调整头寸的最小方差Delta 对冲；（3）当沪铜期货价格波动超过0.4%时，再进行期货头寸调整的对冲；（4）当最小方差Delta 波动超过15%时，再进行期货头寸调整的对冲。本文对四种策略进行对冲回测，分别计算这四种方法的成本，分析其差别，选取了相对较优的对冲方法，并且给予合理的解释。

本文的贡献主要在以下两个方面：

第一，有关期权对冲的现有文献主要集中于对成熟市场的研究，研究的对象主要是上证50ETF 等较为成熟的期权。本文尝试选择较为新兴的品种——沪铜期货期权作为本次研究的对象。此举既丰富了我国商品期货期权领域的研究广度，也在一定程度上为新兴的商品期货期权市场的投资策略提供了参考意见，有助于提高铜产业链相关企业和金融机构中我国沪铜期货市场中的参与度。

第二，本文在研究、对比常规Delta 和最小方差Delta 动态对冲之后，创新性地提出在标的资产价格变化超出一定幅度以及当最小方差Delta 变动超过一定幅度之后再进行对冲这两种方法，从而可以有效减少对冲过度，降低购买期货的成本和手续费，从而减少套期保值的成本，使得最终对冲的盈利效果得到进一步的提升。

二、理论模型

（一）BSM 模型

BSM 模型有如下五个假设：（1）利率已知并且不随时间变化，为常数；（2）股票价格在连续时间内服从几何布朗运动，即其对数收益率的波动率为常数；（3）期权是欧式期权，只能到期行权；（4）买卖股票和期权时没有交易成本；（5）允许任意卖空。

在上述假设成立的前提下，BSM 模型欧式看涨期权定价的公式模型如下所示：

其中，C代表欧式看涨期权价格，St为基础资产（在本文中指铜）在t时刻的价格，N（*）是标准正态分布的分布函数，X代表期权的行权价格，r代表无风险利率，T是期权到期的剩余期限。d1、d2计算方法如下：

其中，σ代表股票对数收益率的波动率，其余变量含义与式（1）相同。

在已知欧式看涨期权价格（C）情况下，对应的欧式看跌期权价格（P）也可以由看涨看跌期权平价公式（Put-Call Parity）来求出，具体公式如下：

当期权标的是期货时，欧式看涨期权价格（C）可以由如下公式得到：

其中，Ft表示t时刻的期货价格。看跌期权价格（P）由平价公式可得

式（1）～（6）中的五个参数St、X、r、T和σ中，只有波动率σ无法从市场数据中直接获得，其余均可观测得到。因此，在已知期权价格的前提下，可以使用BSM 模型的定价公式倒推出波动率σ，即期权的隐含波动率。

（二）局部波动率模型

在BSM 模型中，波动率σ被假定为常数，而事实数据表明，BSM 模型倒推出期权隐含的波动率并不总是常数，存在波动率偏斜、波动率微笑等情况。为了解决这一问题，需要对原先的BSM 模型进行一定程度的拓展，主要分为以下两类：（1）随机波动率模型，即假定波动率服从一个随机游走过程；（2）局部波动率模型。如果随机项σ是标的资产价格和时间的确定性函数，那么这就是局部波动率模型。局部波动率模型是随机波动率模型的一种特殊情况，可以用如下微分方程表示：

其中，r表示无风险利率，d表示股票的分红率，Wt是一个维纳过程。

（三）最小方差Delta

如果使用局部波动率模型计算期权价格，那么期权价格既依赖标的资产当前价格St，也依赖波动率σ。记δMV为局部波动率模型下的最小方差Delta，根据链式求导法则：

由公式（8）可以看出，在局部波动率模型下的Delta 主要由两部分组成，一部分是BSM 模型下的Delta，另外一部分则是由BSM 模型下的vega 乘以作为调整项，但难以估计。

Hull 和White（2017）研究发现，δMV-δBSM，也即公式（8）中的Delta 调整项，可以使用δBSM的二次函数来进行较为准确的拟合，由此得出如下公式：

其中，G（*）表示对应变量的二次函数。

在此基础上，公式（8）可改写为：

其中，a、b、c为常数。

三、对冲实证检验

本文分析了2021年1月4日，不同剩余到期期限的期权交易量（见图1和图2），发现无论对于看涨期权还是看跌期权，剩余期限越长，铜期货期权的交易量越少。剩余期限为三个月（包含三个月）以上的期权的交易量都不到100手。可见市场对铜期货期权的交易主要集中在短期限的期权上。

图1 不同期限的看跌期权交易量

图2 不同期限的看涨期权交易量

因此，本次对沪铜期货期权的对冲研究中，本文选择了剩余期限不足2 个月的3月到期合约。节日前后，交易数据可能会有特殊性，所以，本文避开节日前后（2021年1月1日是元旦，2月12日是春节），选择2021年1月11日至2021年2月4日的数据进行实证验证。

（一）动态Delta 对冲

1.每日调整对冲头寸

假设2021年1月11日某交易商在场内市场做空了100 手标的为沪铜期货合约的期权合约，代码为CU2103C61000（该代码含义为期权买方可以在期权到期日以61000 元的行权价格购买沪铜期货）。《上海期货交易所阴极铜期货期权合约》规定合约标的物为阴极铜期货合约（5 吨），报价单位是元（人民币）/吨，《上海期货交易所阴极铜期货合约》规定交易单位为5 吨/手，报价单位为元（人民币）/吨。为了凸显套期保值成本的本质，本文在实证中的计算均假设期权的标的物为阴极铜期货合约（1 吨），所以在实际操作中，期权的盈利和期货套期保值的成本都是本文所得数据的5 倍。

在2021年1月11日当天，该份期权合约的标的资产，铜期货合约的市场价格为58670 元/吨，该期权的Delta 为0.23，在对冲起始日，为了对冲100 手沪铜期权空头，需要做多100×Delta=23 手沪铜期货合约。本文假设期货交易费用为买入期货成本的0.15‰，所以开仓手续费为23×58670×0.15‰=202.41 元。同时，期权卖方可以收入权利金826×100=82600 元。接下去本文考虑2021年1月11日至2021年2月4日每日调整的经典BSM 模型下Delta 动态对冲策略，结果如表1所示。

表1 每日调整的常规Delta 动态对冲策略结果

由表1可以看出，到1月12日收盘时，Delta 值上升至0.26，为了保持Delta 中性，需要做多2.52 手沪铜期货合约。以此类推，为了保持对冲组合的Delta 中性，需要每天进行仓位的调整。若Delta 值变大，则做多沪铜期货，若Delta 值变小，则需要平仓部分期货。到2月4日，将所持沪铜期货头寸全部平仓，则利用沪铜期货对沪铜期货期权进行Delta 动态对冲的累积成本为27617.86 元，即期货市场亏损27617.86 元。其中，所付出的手续费共344.36 元，未平仓量0 手。

2.最小方差Delta 对冲

由于期权价格和标的资产的价格变动为如下所示：

结合公式（10）、公式（11），可以推导出如下公式：

根据公式（12），本文选取2020年12月3日至12月31日一个月的数据进行回归，估计出a、b、c的值，并且根据a、b、c的值来调整BSM 模型测算出1月份的最小方差Delta，使用最小方差Delta 进行对冲。

回归出的方程如下所示：

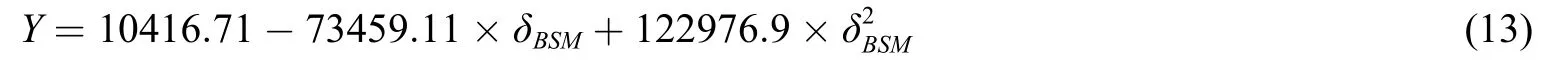
由此可见，公式（12）中的a为10416.71，b为-73459.11，c为122976.9，在此基础上，用公式（10）对BSM 模型求出的δBSM进行调整，得到δMV也即最小方差Delta，表格2 列出对冲过程，具体逻辑同方法一BSM 模型下Delta 对冲。

从表2可以看出，使用调整后的最小方差Delta 进行对冲，对冲的累计成本为23914.69 元，即期货市场亏损23914.69 元，其中，手续费782.08 元，未平仓量0 手。

表2 每日调整的最小方差Delta 动态对冲策略结果

3.期货价格变动超出设定范围的Delta 对冲

此外，本文在最小方差Delta 的基础上进行改进，当标的资产价格变动不超过一定范围时，风险可控，所以不进行期货头寸调整，这样来减少Delta 过度对冲。本文将调整的范围定为0.4%，即当标的资产价格变动超过上一次调整日价格的0.4%时，再进行期货头寸的调整。对冲过程如表3所示。

由表3可以看出，2021年1月11日对冲开始时，最小方差Delta 为0.23，因此买入23 手期货建仓，花费成本为1349410.00 元，手续费为202.41 元。2021年1月18日，期货收盘价为59280 元，相较于2021年1月11日时价格变动超过0.4%，因此进行对冲的头寸调整，此时最小方差Delta 为0.17，所以卖出6.45 手期货。之后以此类推，当期货价格变动相较于上一次调整日的价格超过0.4%时进行对冲头寸的调整，于是分别在1月18日，1月19日，1月21日，1月22日，1月25～28日，2月2日，2月3日进行对冲。 此方法相比于对冲策略2 减少了对冲频率，最终花费的手续费为731.25 元，购买期货成本为22189.80 元，最终累计成本为22921.05 元，即期货市场亏损22921.05 元，未平仓量0 手。

表3 超出设定范围调整的最小方差Delta 对冲效果

4.最小方差Delta 变动超出设定范围的Delta 对冲

除了根据期货价格变动幅度进行期货头寸的调整外，本文提出一种新的对冲方式。本文认为，最小方差Delta 的变动幅度不超过一定范围时，期权风险可控，此时可以不进行期货头寸调整。本次实证中将该调整的范围定为15%，即当最小方差Delta 值的变动幅度超过上一次调整日最小方差Delta 的15%时，再进行期货头寸的调整，下面通过表4对对冲过程予以体现。

由表4可以看出，2021年1月11日，根据最小方差Delta 进行建仓，购买了23 手期货，成本为1349410.00 元，花费手续费202.41 元。2021年1月12日，由于最小方差Delta 变动为0.19，相较于2021年1月11日最小方差Delta 的0.23，减少了17.39%，超过了设定的范围15%，因此进行期货头寸的调整，卖出4.40 手期货，随后的日子最小方差Delta 的变动并未超过15%，所以一直不进行期货头寸的调整，直到1月26日，最小方差Delta 为0.42，相较于上一次进行头寸调整日2021年1月12日的最小方差Delta 0.19，变动幅度较大，为121.05%，因此买入了22.97 手期货，花费成本为1342799.11 元，所需的手续费为201.42 元。采用这种对冲方法，仅在开始和结束对冲的当天，以及1月12日、1月26日、1月27日、1月28日进行了期货头寸的调整，进一步减少了对冲频率，最终花费的手续费为682.27 元，购买期货的成本总计为20779.79 元，两者加总得到最终的累计成本为21462.06 元，也即期货市场亏损21462.06 元，未平仓量0 手。

表4 最小方差Delta 波动超出范围进行头寸调整对冲效果

与此同时，在期货市场上无论用哪一种套期保值策略进行Delta 对冲期权风险，期权市场的盈亏计算如下：2021年1月11日做空100 手CU2103C61000 期权，直到2021年2月4日平仓。期权市场盈利(826－120)×100=70600 元。

（二）实证结论

上述四种动态Delta 对冲策略效果如表5所示。

表5 四种Delta 对冲效果比较

由表5可以看出，期货是为期权套期保值，对冲风险，所以当期权盈利时，期货是亏损的。另外可以看到，每日调整的最小方差Delta 对冲最后的总收益高于每日调整的常规的BSM 动态Delta 对冲，而期货价格超出一定范围后再进行期货头寸调整的最小方差Delta 对冲收益高于之前两种对冲方式，而当最小方差Delta 超出一定范围后再进行期货头寸调整的对冲方式的收益最高，在此次实证中是最优的套期保值策略。本文分析原因如下：在本次实证中，方法（2）相对于方法（1），减少了过度对冲，在第（3）、第（4）种对冲方法中，由于对对冲的执行设置了门槛，既将期权风险控制在一定范围内，又相较于每日调整的最小方差Delta 对冲，降低了购买期货的成本和手续费，从而减少了期货套期保值的成本。本次实证中，相较于根据期货价格波动幅度来进行期货头寸调整的方法，根据最小方差Delta 波动幅度来进行期货头寸调整，进一步减少了对冲的频率，减少了对冲的成本，从而成为了四种动态Delta 对冲中的最优策略。同时，本次实证表明，进行风险管理过后与裸露的期权头寸具有较大的盈利差别，作为投资者，在市场上进行投资的同时，需要时刻注意风险敞口的管理。

四、未来展望

在前述研究基础上，本文对于未来有关期权对冲相关的研究方向提出了以下几点展望：

（一）拓宽研究范围

本文有关最小方差Delta 的调整仅仅局限于Hull 和White（2017）二次模型方法，此外还有著名的SABR 模型等，将来有关最小方差Delta 的调整可以涉及更多相关的理论模型，调整方法更为全面，进一步提高调整精度。

（二）开发交易策略

本文有关最小方差Delta 的研究可以开阔期权交易员们对于期权交易策略的思路，采用更加精确的模型修正自己的交易策略，当常规对冲方式遭遇瓶颈之时，可采用最小方差 Delta 进行对冲，可能取得意想不到的效果。

另外，随着科技发展，人工智能投资顾问、大数据拟合和预测使用范围越来越广泛，后续可以考虑将最小方差Delta 对冲策略、人工智能投资顾问与大数据相结合，加以推广运用。