稳态法实验研究Ga68 In20 Sn12 液态金属界面热阻特性

张 岩 许锦阳 洪芳军

(上海交通大学机械与动力工程学院 上海 200240)

1 引 言

近年来,为了满足高性能和有限空间的要求,功率电子设备朝着微型化和集成化的方向发展[1]。根据摩尔定律,芯片的晶体管数量每两年就会增加一倍[2],其集成化随之带来了热挑战。电子设备产生的热量导致温度升高,而当运行温度超过耐温限制时,设备即会降频低功率运行或甚至由于长时间超温损坏,因此电子设备需配有相应合适的散热装置。在封装工艺中,电子器件与散热装置间存在固体接触界面,当界面接触性较差,使得接触热阻过大,继而恶化传热过程,降低换热器件的散热性能。

对于两个宏观直接接触的固体表面,其实际微观接触仅在一些离散的面单元,未接触的界面间隙存在空气,而空气的导热性能较差(20 ℃时导热系数为0.025 9 W/(m·K),热量以导热方式穿过该气体层时,导热热阻随之显著增加。由此,学者们针对其界面热阻特性进行了相应的模拟和实验研究。毕冬梅等人[4]对铜-不锈钢接触热阻进行低温实验和模拟研究,仿真结果表明在温度低于150 K 时温度和压力对接触热阻影响比较明显。刘东欢[3]等人实验测试了C/C 复合材料与高温合金GH6000 的接触热阻,当未采用热界面材料时,接触热阻范围在10-3—10-5m2·K/W。由上可以看出,现有工艺条件下固体表面间直接接触热阻较大,对换热性能影响较大。

目前,常用降低接触热阻的方法是在固体接触界面填充热热界面材料,如导热硅脂、相变材料、导热硅胶片等,这些材料是通过添加导热颗粒提高导热性能的聚合物材料。龙巍[5]采用接触热阻稳态法实验测试了HY880 和Rocket 膏状热界面材料的导热系数和界面热阻,HY880 的导热系数低于Rocket,但是其与铜片的界面热阻却低于后者,证明界面热阻不仅取决于导热系数,也受到界面材料和固体表面的润湿性、粗糙度等因素影响。袁超[6]采用接触热阻稳态法测试硅油和导热硅脂与固体基板的接触热阻,试验测得其范围在5.87—150 ×10-6m2·K/W。由此可见,相较于固体表面直接接触,添加热界面材料使得接触热阻降低10—102数量级。此外,碳纳米管作为新型热界面材料,具有无污染、耐高温等特点,黄正兴[7]采用瞬态热反射法测试了采用碳纳米管阵列-Au 界面接触热阻,结果显示在1.49 MPa 的压力,界面接触热阻介于1.90—3.51 mm2·K/W。

传统的热界面材料存在导热系数低、接触性差、易老化、易分层等缺点,液态金属由于其高导热系数、流动性较好、填充性好等特性受到越来越多的关注[8]。Zhao 等人[9]实验测试了液态金属的导热特性,并研究表面粗糙度、压力等对界面热阻的影响,实验结果表明界面温度达到液态金属熔点50—60 ℃,液态金属的高流动性显著降低接触热阻(由200—250 mm2·K/W 降低至0—50 mm2·K/W)。Ge 等人[10]将熔点为63 ℃的液态金属均匀包裹在氮化硼纳米材料上,该复合界面材料将接触热阻由13.8 ×10-4m2·K/W 降低至0.547 ×10-4m2·K/W。纪玉龙等人[11]制备了以液态金属Ga62.5In21.5Sn16为基体,掺杂0.5—50 μm 铜粉的热界面材料,实验结果表明随着铜粉粒径的减小,热界面材料的导热性能逐渐增强。Chu 等人[12]实验测试了在800 kPa 接触压力下,采用In52Sn48液态金属的接触热阻可降低至0.011 K/W,为了限制实验中液态金属溢出问题,提出铟限制密封设计。通过上述研究可以看出,液态金属具有高导热系数、优异的界面填充能力、降低界面接触热阻的特点,但是研究中并未对液态金属接触热阻实验平台进行可靠性验证,同时没有对电子设备升降温工况下的接触热阻变化进行研究。

本文针对Ga68In20Sn12低温液态金属进行了接触热阻实验研究,验证了该实验平台的可靠性,并研究了界面压力、界面温度和表面特性等因素对界面接触热阻的影响规律,为低温液态金属作为热界面材料的应用提供了实验指导。

2 实验系统及方法

2.1 接触热阻测量实验系统

接触热阻是由于两固体表面不完全接触造成,固体接触界面两侧具有连续的热流,但存在温度梯度,其定义为:

式中:ΔT为接触界面两侧温差,K;q为通过接触界面的热流密度,W/m2。

本研究采用接触热阻稳态法测量Ga68In20Sn12[13](密度为6 363.2 kg/m3,熔点为10.8 ℃)低温液态金属接触热阻,实验系统如图1 所示。实验系统由接触热阻实验段、数据采集系统、冷却水循环系统以及模拟热源组成。其中,接触热阻实验段系统依据ASTM D5470 标准[14]进行设计安装,其主要部件为控压装置、冷板、实验试件、加热铜块、电热管。控压装置由不锈钢板、弹簧及螺栓组成,用于控制试件接触面压力及实验段整体固定。实验试件接触面为直径20 mm的圆形器件,材质为T2 紫铜。试件侧边加工有深度为10 mm,直径为0.8 mm 的热电偶测温孔,测点分布如图2 所示。通过在试件内部安装T 型热电偶,测量试件内部温度分布。

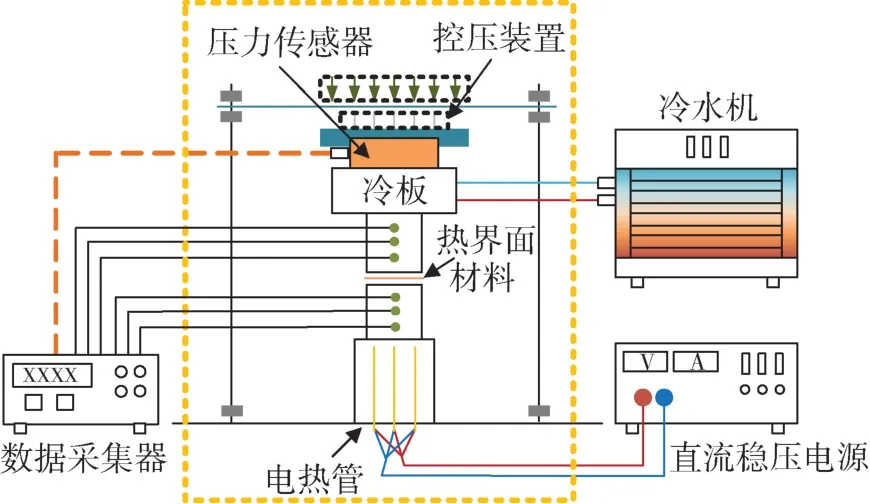
图1 接触热阻实验系统示意图Fig.1 Schematic diagram of experimental system for thermal resistance

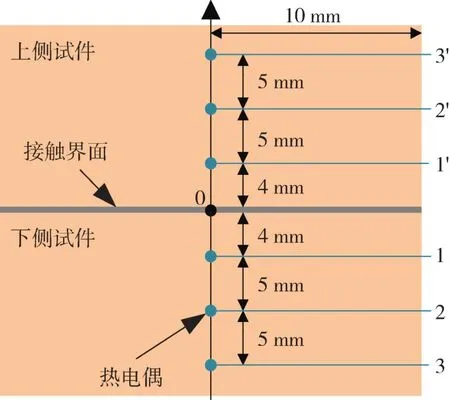
图2 测温点分布示意图Fig.2 Schematic diagram of temperature measuring point distribution

当系统运行时,电热管产生的热量通过加热铜块、高温试件、热界面材料、低温试件、冷板进行传递,最终经冷板中的循环冷却水进行散热。同时为了减少接触热阻实验段系统沿径向散失热量,采用合成石(厚度为20 mm,导热系数0.25 W/(m·K))作为保温外壳。通过施加外部压力,两根等截面圆柱试件保持轴向接触。为了维持试件表面的均匀稳定温差,对一端面进行加热,对另一端面进行冷却,对圆柱试件侧边进行保温处理,由此保证热量传递近似为轴向一维热传导过程。实验测量轴向测温点温度,根据傅里叶导热定律得到轴向传递的热流密度和接触界面温差,进而计算接触界面的接触热阻。

实验段采用压缩弹簧为试件表面施加压力,并通过布置在冷板和控压装置间的受力传感器,测量施加在试件表面的压力。试件顶部采用T2 紫铜材质的蛇形通道冷板冷却,其通道高宽为5 mm,通道肋宽1 mm。在试件与冷板和加热铜块接触面均匀涂抹导热硅脂,以减小该位置接触热阻。上述实验系统主要器件型号和规格如表1 所示,实验数据采用安捷伦34970A 数据采集装置自动采集。

表1 实验设备型号及规格Table 1 Model and specification of testing devices

2.2 数据处理

根据傅里叶导热定律计算通过试件的热流密度q为:

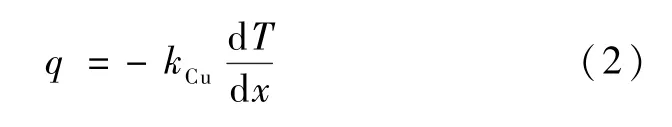
式中:kCu为试件导热系数(380 W/(m·K)。温度梯度dT/dx采用一阶泰勒展开式进行计算:

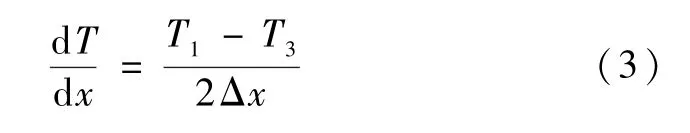
式中:T1和T3由布置在测温点1、3 温度,K;Δx为相邻测温点的距离,mm。测温点2 用于分析试件测温点的线性偏差,确定测温数据可靠性。

为了进一步评估测温点温度线性偏差对结果的影响程度,定义了线性偏差(ε)如下所示:

式中:T(2)为T1、T3平均值,K。同理,测温点1’、2’、3’的热流密度和线性偏差采用类似的处理方法。

实验过程中采用界面两侧热流密度(上侧试件qup,W/m2;下侧试件qdown,W/m2)算术平均值作为轴向热流密度测量值,即:

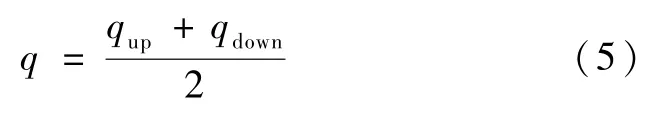
实验通过一维傅里叶导热定律计算试件接触表面高温侧温度T+和低温测温度T-:

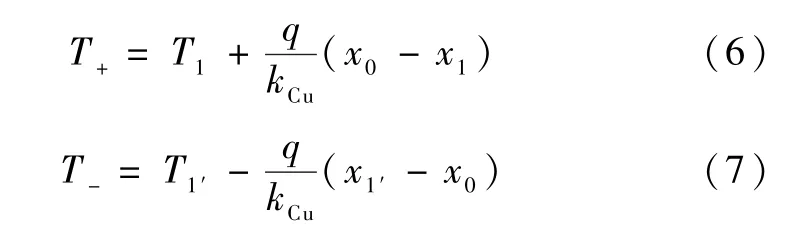
通过接触面温差和轴向热流密度计算接触热阻:

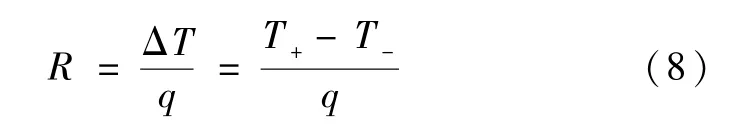
实验采用两试件表面温度的算术平均值作为液态金属的定性温度:

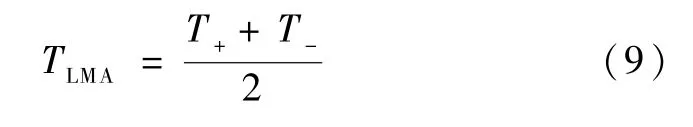
试件接触表面所受到的压力值,如下式所示:

式中:F为施加于试件表面的力,N;A为实验试件接触面面积,m2。

3 结果与讨论

3.1 温度变化规律可靠性验证

本次实验中控制冷却水入口温度10 ℃,液态金属均匀涂抹在铜试件接触表面,图3 和图4 所示分别为在界面压力为197 kPa,热流密度为52.7 W/cm2工况下主要测点温度和测温点2、2’的线性偏差随时间的变化规律。由图3 可见,在恒定热流工况下,各测温点能够保持稳定,温度波动在±0.1 K 以内。这是因为T 型热电偶测温精度(±0.1 K)和数据集采集器仪器误差(±0.01 K)造成。测温点2、2’存在线性偏差,且温度高于温度(2)、(2’),这是因为实验试件的保温结构并不能完全防止漏热发生,因此轴向的温度分布并不是严格遵循线性分布。

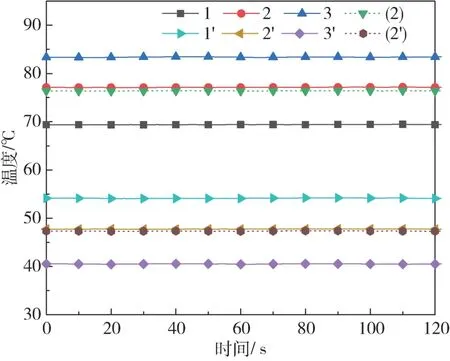
图3 热流下恒定热流各测点温度-时间(P=197 kPa, q=52.7 W/m2)Fig.3 Temperature of each measurement point when fix heat flux (P=197 kPa,q=52.7 W/m2)

由图4 可知稳态测量时两试件有不同程度的线性偏差,下端试件的偏差高于上端试件,这是因为下端试件温度高于上端试件,漏热相对较多。两试件测温点的线性偏差均小于＜6%,测量温度近似作为线性温度处理,因此采用测温点1、3、1’、3’数据进行热流密度计算具有合理性。

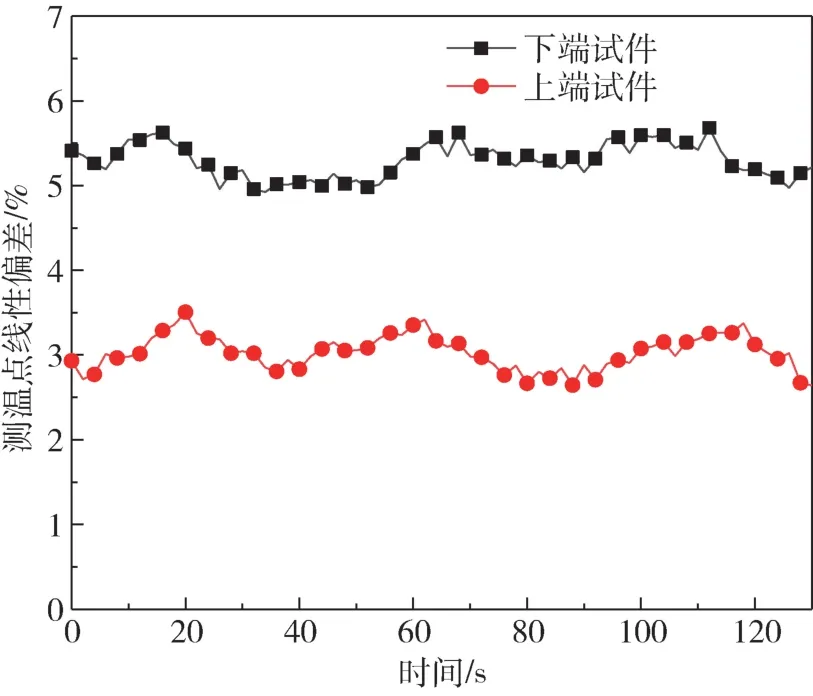
图4 测温点线性偏差-时间(P=197 kPa,q=52.7 W/cm2)Fig.4 Curves temperature of measurement point linear deviation versus time (P=197 kPa, q=52.7 W/cm2)

实验结果表明自主设计搭建用于低温液态金属接触热阻实验装置具有可靠性,测温点温度具有稳定性,实验测温点温度能够代表该测温界面的温度,试件内部温度可视为一维线性分布。

3.2 液态金属优异性验证

图5 所示为热流密度15.60 W/cm2时不同压力下导热硅脂和液态金属作为铜试件之间的热界面材料的接触热阻。由图可知,当压力从74 —369 kPa时,导热硅脂作为界面材料接触热阻逐渐下降,从2.09 ×10-5m2·K/W 降低至5.36 ×10-6m2·K/W,降低了74.36%,这是因为压力的增加造成导热硅脂的厚度不断降低,其表面的微观变形填充试件表面的缝隙,增加传热面积。液态金属作为高流动性的工质,其在74 kPa 压力下即可填充试件表面的间隙,此时其接触热阻为6.12 ×10-6m2·K/W,相较于同压力的导热硅脂降低了71%。表明液态金属在低界面压力表现出低接触热阻的优异性。

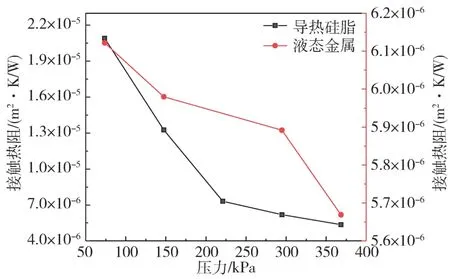
图5 不同界面材料下压力对接触热阻影响Fig.5 Dependence of pressure on system thermal resistance for different interface material

3.3 液态金属作为界面材料接触热阻试验研究

图6 所示为不同界面压力和温度下,铜表面间添加液态金属工况的接触热阻变化特性,铜表面间添加液态金属工况为铜接触表面间添加液态金属,图7 所示为液态金属导热系数随温度变化趋势。当界面温度为304—357 K,采用液态金属作为界面材料时,接触热阻逐渐升高,压力为270 kPa 时,温度的升高造成接触热阻从6.78 ×10-6m2·K/W 增加至8.42 ×10-6m2·K/W,增加了24%。这是因为温度升高造成试件表面间液态金属导热系数降低,进而降低了界面传热能力。当压力为123—270 kPa 时,接触热阻随着压力的增加而降低,温度为304 K 时,压力的增加造成接触热阻从7.59 × 10-6m2·K/W 降低至6.78 ×10-6m2·K/W,降低了7.05%,这是因为压力增加使液态金属更好地填充试件表面缝隙。

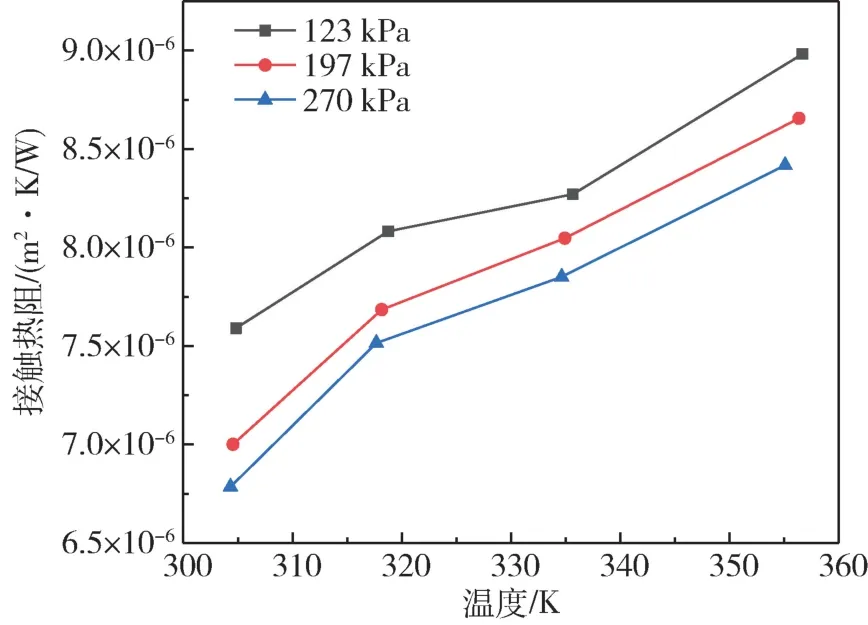
图6 铜-铜界面材料下压力和温度对接触热阻影响Fig.6 Variation of thermal resistance under different pressures and temperatures at copper interface

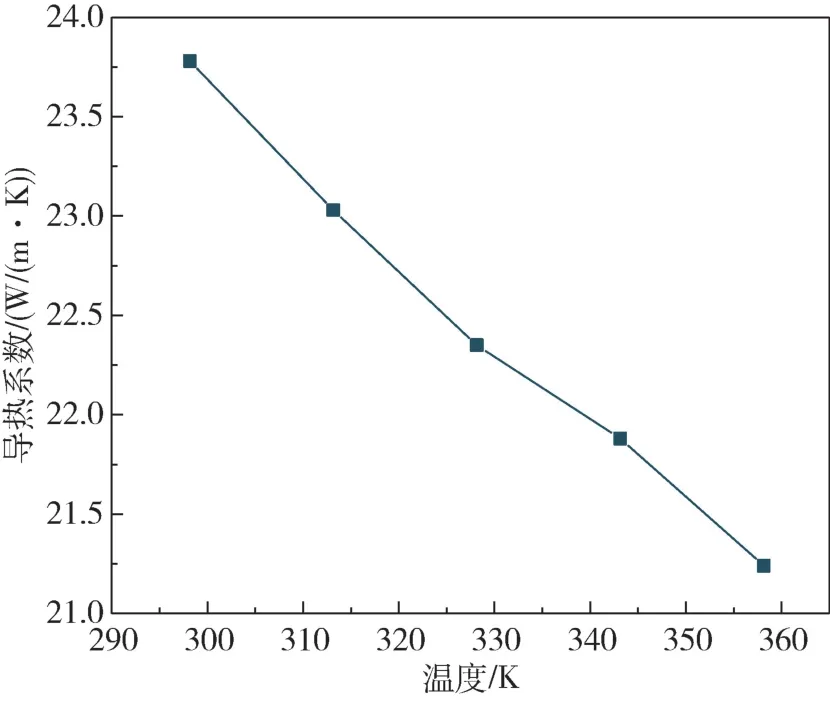
图7 液态金属导热系数随温度变化规律Fig.7 Variation of thermal conductivity of liquid metal at different temperatures

图8 所示为压力为197 kPa 和不同界面温度下,镀镍表面和铜表面间添加液态金属工况下接触热阻的对比,两者均随着界面温度的增加而增加,与铜表面工况相对比,镀镍表面工况接触热阻明显更大。界面温度为305 K 左右时,镀镍表面工况下接触热阻为2.66 ×10-5m2·K/W,为铜表面工况下7.0×10-6m2·K/W 的3.8 倍。

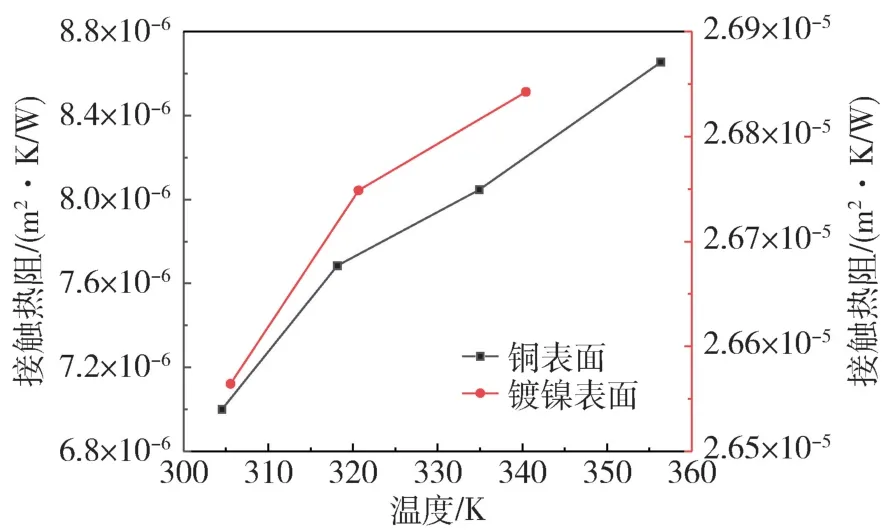
图8 镀镍表面下温度对接触热阻影响Fig.8 Dependence of thermal resistance under different pressure and temperature at nickel plated surface

图9 为SEM 拍摄的机加工铜表面和镀镍铜表面,在相同观察倍率下,渡镍表面显示出低粗糙特征,有利于降低接触热阻。CCD 相机拍摄铜表面、镀镍铜表面上方液态金属如图10 所示,经ImageJ 软件计算,液态金属与铜表面和镀镍表面的接触角分别为145.3°和128.2°,镀镍过程降低了液态金属与试件表面的接触角,也有利于降低接触热阻。但如图11所示,液态金属中的Ga 能够在铜表面发生腐蚀生成CuGa2,与铜表面形成致密接触,增加其界面热量传递能力,而液态金属和渡镍防腐涂层表面,不能发生反应,并且无法通过外力将其和渡镍表面黏合,该特征增加其与界面的接触热阻。

图9 铜表面和镀镍铜表面Fig.9 Copper surface and nickel-plated surface

图10 液态金属表面接触角Fig.10 Contact angle of liquid metal

图11 铜表面和镀镍表面液态金属浸润性Fig.11 Wettability of liquid metal on copper and nickel plated surfaces

4 结 论

针对Ga68In20Sn12液态金属作为热界面材料的接触热阻测量进行了实验研究,验证了实验系统的可靠性,对比分析了常规导热硅脂和液态金属热界面材料的传热特性,讨论了温度、压力和表面特性对接触热阻的影响规律,主要结论如下:

(1)通过恒热流工况下测温点温度的变化规律及测温点线性偏差,验证了该实验系统的结果具有可靠性。

(2)研究了导热硅脂和液态金属在不同压力下的接触热阻特性,在74 kPa 的低压工况下,液态金属的接触热阻相较于导热硅脂降低了71%,表明液态金属作为热界面材料具有很高的应用价值。

(3)采用液态金属作为热界面材料,界面温度的升高导致界面接触热阻增大,压力为270 kPa 时,温度从304 K 增加至357 K 导致接触热阻增加24%。

(4)铜表面镀镍过程虽能够有效防止液态金属对铜表面腐蚀,但却明显增大界面接触热阻,其原因是液态金属无法黏合镀镍表面。