Robustness measurement of scale-free networks based on motif entropy

Yun-Yun Yang(杨云云) Biao Feng(冯彪) Liao Zhang(张辽)

Shu-Hong Xue(薛舒红)1, Xin-Lin Xie(谢新林)2, and Jian-Rong Wang(王建荣)3

1College of Electrical and Power Engineering,Taiyuan University of Technology,Taiyuan 030024,China

2Taiyuan University of Science and Technology,Taiyuan 030024,China

3School of Mathematical Sciences,Shanxi University,Taiyuan 030024,China

Keywords: motif,network robustness,scale-free,entropy

1. Introduction

Complex network is one of the methods to model and study the actual complex systems.[1]With the in-depth study of the related characteristics of complex networks, network robustness has gradually attracted the extensive attention of scholars. The so-called network robustness refers to the ability of the network to maintain the integrity and function of the original network structure after being subjected to random failures or deliberate attacks.

According to the current work on network robustness,the measurement of network robustness is mainly carried out around nodes. Albertet al.[2]investigated the random attacks and deliberate attacks on nodes in scale-free networks and random networks, and calculated the change of network diameter and the largest connected subgraph, and they confirmed the strong robustness of scale-free networks to random attacks and their vulnerability to deliberate attacks. Newman and Ghoshal[3]randomly removed nodes on real networks of different scales, and analyzed the robustness of the network by using the variation of two components in the network.Clemente and Cornaro[4]proposed to use the eigenvalue of the Laplace matrix of the network to calculate the Kirchhoff index,[5,6]then they calculated the effective resistance centrality based on nodes and edges respectively according to the Kirchhoff index,and they used the centrality value to measure the robustness of the network,and presented different calculation methods for different types of networks.

For different nodes, the coupling strength of the node itself determines its influence on the network robustness, and nodes with large degrees are more sensitive to random attacks, showed the unity of dynamic robustness and structural robustness.[7]Kasthurirathnaet al.[8]continuously attacked the scale-free network according to the node degree value,they used the average path length and clustering coefficient to measure the robustness. It was confirmed that the average path length is positively correlated with the network robustness,and the clustering coefficient is negatively correlated with the network robustness. Zhouet al.[9]used the Betti number to calculate the number of structural holes. Through random attacks and deliberate attacks on the network, it was found that the number of structural holes can change with the attack intensity. For power networks[10,11]and urban transportation networks,[12–15]they proved to have the characteristics of the scale-free network and small-world network,that is,they are robust under random attacks and weak under deliberate attacks.Other researches of network robustness include the using of node efficiency,[16]R-index,[17]fractal dimension,[18]natural connectivity[19]to measure the network robustness.

The research process of complex network itself is complex generally. But the research from the low-order perspective of nodes and edges turns relatively simple. The research from the high-order perspective can realize the transformation from low to high complexity, which is the general law of research problems. New rules and new properties can also be found with the help of high-order structure. For many actual complex networks,they are usually scale-free,and motifs appear frequently in the form of high-order structure. Compared with nodes, motifs have the characteristics of large number,complex types and strong correlation, which play a decisive role in the overall structure and function of the network.[21]However, previous research work on network robustness ignored the existence of motifs. At the same time,in the actual complex systems, the probability of random failures is often higher than that of deliberate attacks. Therefore,we will study the robustness of scale-free networks from the perspective of motif,propose an entropy of node degree distribution based on motif to measure the robustness of different sizes of scale-free networks under random attacks, and verify its effectiveness and superiority through experimental analysis.

2. Theoretical basis

2.1. Scale-free networks

The scale-free network[22]is a classical complex network model, and its node degree distribution function obeys the power-law distribution, that is,P(k)=Ck−γ, whereCis the scale coefficient,kis the degree value of the node,γis the exponent and usuallyγ ∈[2,3].In a scale-free network, the degree value of most nodes is very small,and a few hub nodes have large degree value.

In order to realize the construction of scale-free network,Barab´asi and Albert[23]proposed a simple and effective construction model—BA scale-free network,that is,on the basis of a randomly generated small network,BA scale-free network is generated according to the growth mechanism and preference connection mechanism. The growth mechanism refers to adding a new node to the original network at each time step,while the preference connection mechanism refers to that the newly added nodes tend to connect with the hub nodes in the original network. For a BA scale-free network withN=100 andM=3,the generation process is as follows: when a new node is added to the network,M=3 edges will be added to the network until the scale of the network reachesN=100 nodes.

2.2. Network motif

Motif is a kind of subgraph that appears frequently in the network. Motif plays a decisive role in the function and properties in the whole network. Identifying and analyzing motifs is helpful in revealing the dynamic and structural characteristics of the network. There have been many algorithms for recognizing and detecting the network motif.In this work,the software FANDOM[24]developed based on the ESU algorithm[25]is used to mine motifs. According to the number of nodes contained in the motif (n), the motif can be defined as ann-order motif. The specific structure of the possible 3rd motif and the 4th-order motif in the simple undirected network are shown in Figs.1 and 2,respectively.

The most important statistical feature of the motif is theZ-score. The positive or negativeZ-score can be used to determine whether the motif appears in the network. The presence of the motif can be confirmed only whenZ>0. The value ofZcan be calculated from the following formula:

Fig.1. The third-order motifs of undirected network.

Fig.2. The fourth-order motifs of undirected network.

3. Entropy of node degree distribution based on motif

Let the graphG=(V,E)be an undirected and unweighted network, whereV={v1,v2,...,vN}is a set of nodes in the network,Nrepresents the total number of nodes,E={e1,e2,...,eL}refers to a set of edges in the network, andLdenotes the total number of edges.

The classical node degree value refers to the total number of edges owned by the node, but this calculation method ignores the existence of motifs in the network. According to this,Hanet al.[26]proposed a motif-based node degree value,which is specifically defined as follows: for a networkG, letMbe the motif ofG,the total number of motifMcomposed of nodeiis defined as the motif-based node degree value of nodei. In this work, the traditional node degree distribution value is extended to the node degree distribution value based on motif,and the entropy of node degree distribution based on motif,that isHM,is further obtained,and its specific expression is

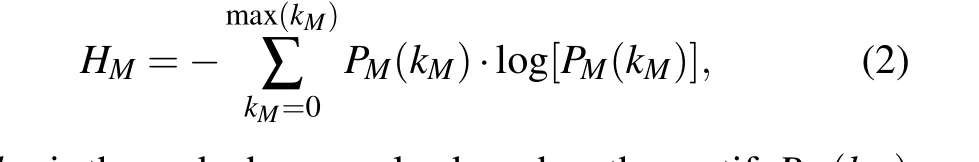
wherekMis the node degree value based on the motif,PM(kM)is the node degree distribution value based on the motif, that is, the node degree value based on the motif is equal to the probability of the occurrence ofkM. In the following, experimental results will show that the larger the value ofHM, the more robust the network is. In the process of calculation, it can be found thatkMdoes not change continuously,so it is not calculated for the case ofPM(kM)=0.

4. Experiment and analysis

In this work,all experimental networks are undirected and unweighted.In order to verify the effectiveness of our method,we will useHM,and some classical robustness metrics,such as average edge betweennessBG,[18]network efficiencyEG,[18]and network dispersionDG,[27]to analyze the robustness of BA scale-free networks. At the same time, by analyzing the computational complexity of different indicators, the superiority of our method is highlighted. The 3rd-order motifs are used in the experiment unless otherwise specified.

Definition 1 Edge betweennessBe[27]is one of the criteria to measure edge centrality based on the shortest path,and its calculation formula is as follows:

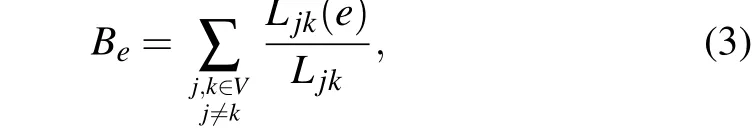
whereBerepresents the betweenness value of edgee,Ljkis the length of the shortest path from nodejto nodek, andLjk(e)refers to the length of the shortest path from nodejto nodekthrough edgee.

Definition 2 For the networkG, the average edge betweennessBGis one of the indicators to measure the robustness of the network from a local perspective,which is defined as follows:

whereLjkrepresents the length of the shortest path from nodejto nodek,nis the total number of edges in networkG,Vrefers to the set of all edges in networkG, and the larger the value ofEG,the stronger the robustness of the network is.

Definition 4 For the networkG,network dispersionDGis one of the indicators to measure the robustness of the network from a local perspective,which is defined as follows:

whereLjkrepresents the length of the shortest path from nodejto nodek,DG ∈[0,1], and the greater the value ofDG, the greater the dispersion of the network is and the worse the robustness of the network.

4.1. Robustness of BA scale-free networks to random attacks

In this subsection,we will use different indicators to measure the robustness of BA scale-free networks under random attacks,and analyze the relationship between node degree distribution function based on motif,HM, and network robustness.

4.1.1. BA scale-free network robustness measurement

In experiment,nine different BA scale-free networks are generated according to the growth mechanism and preference connection mechanism. The calculation results of its basic attributes and robustness metricsHM,BG,andEGare shown in Tables 1–3.

By analyzing the data in Tables 1–3,it can be found that for BA scale-free networks, whenNis the same, the larger the value ofM, the smaller the average edge betweenness is, the higher the network efficiency, and the greater the entropy of node degree distribution based on motif, that is, the stronger the robustness of the network is;whenMis the same,the smaller the value ofN, the smaller the average edge betweenness is,the higher the network efficiency,and the greater the entropy of node degree distribution based on motif, the stronger the robustness of the network.

Table 1. Robustness index of BA scale-free networks(N=100).

Table 2. Robustness index of BA scale-free networks(N=300).

Table 3. Robustness index of BA scale-free networks(N=600).

Fig.3. Dispersion curves of BA scale-free networks under random attacks(N is the same)for N=100(a),300(b),and 600(c).

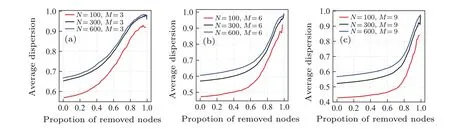
Fig.4. Dispersion curves of BA scale-free networks under random attacks(M is the same)for M=3(a),6(b),and 9(c).

In order to analyze the robustness of BA scale-free network under random attacks by using network dispersion, we use the method of randomly removing nodes to destroy the network, randomly removing one node each time, conducting 100 independent experiments on each network, and then calculating the average value of network dispersion obtained from 100 independent experiments. The dispersion curves are shown in Figs.3 and 4.

In Figs.3 and 4,the abscissa represents the proportion of removed nodes,and the ordinate represents the average value of network dispersion obtained from 100 independent experiments. Since we remove nodes from the network randomly,when the number of removed nodes is large enough, there may be only one edge left in the network. Combining with formula(6),it can be seen that the network dispersion will become 0, which will reduce the average value of network dispersion obtained from 100 independent experiments to a certain extent,that is,the average dispersion of the network will be infinitely close to 1,but it may not be equal to 1.

In Fig. 3, from the overall change trend of the curve it follows that for the BA scale-free networks,when the network scaleNis the same, the larger the number of edgesMin the preferred connection, the smaller the dispersion in the whole process of random attacks is, that is, the stronger the robustness of the network is. At the same time,it can be found from Fig.4 that for BA scale-free networks,ifMin the preference connection is the same, the smaller the network scaleN, the smaller the dispersion in the whole process of random attacks is,that is,the stronger the robustness of the network.

The experiment on BA scale-free networks shows that the measurement results ofHM,BG,EG, andDGon network robustness are consistent with each other,which verifies the effectiveness ofHMin measuring network robustness. That is,in the BA scale-free network,HM,the entropy of node degree distribution based on motif can be used as a new network robustness measurement index.

4.1.2. Analysis of cause for HM change

It can be found from Eq. (2) thatHMis related tokMandPM(kM), the node degree distribution function based on motif is a comprehensive representation ofkMandPM(kM).Therefore,for BA scale-free networks,we first study the node degree distribution function based on motif, and then further analyze the relationship between the node degree distribution function based on motif andHM.

The node degree based on the motif is a generalization of the traditional node degree. In the BA scale-free networks,the traditional node degree distribution function obeys the powerlaw distribution. Therefore, it is of research significance to fit the node degree distribution function based on the motif according to the power-law distribution and judge whether it obeys the power-law distribution through the fitting results.

For the nine BA scale-free networks involved in Subsubsection 4.1.1, we will fit the traditional degree distribution function and the node degree distribution function based on the motif by power-law distribution. The curve fitting results and index calculation values are shown in Figs.5 and 6.

By observing Figs.5 and 6,it can be found that in the BA scale-free networks, like the traditional node degree distribution function, the node degree distribution function based on motif can be well fitted by power-law distribution. WhenNis the same andMincreases gradually,the heavy-tailed distribution of the node degree distribution function based on the motif becomes more obvious, that is, the number of nodes with a larger motif degree becomes larger, resulting in largerHMand stronger robustness. WhenMis the same andNincreases gradually,although there is still a heavy-tailed distribution,the frequency of node degree value based on motif at a small value will gradually increase, that is, the number of nodes with a small motif degree value will increase,resulting in smallerHMand weaker network robustness.

The statistical data shown in Table 4 can be obtained by combining the entropy of node degree distribution based on motif with results in Figs.5 and 6.

Fig.5. Traditional degree distribution curve of BA scale-free networks for N=100(a),300(b),and 600(c).

Fig.6. Motif-based node degree distribution curve of BA scale-free networks,for N=100(a),300(b),and 600(c).

Table 4. Entropy of node degree distribution based on motif and index γ.

It can be found from Table 4 that for the BA scale-free networks,whenNis the same andMgradually increases,the trend ofHM,that is,the changing trend of network robustness is the same as that ofγ1, but opposite toγ2. WhenMis the same andNincreases gradually, the trend ofHM, that is, the changing trend of network robustness andγ2are opposite to each other.

4.2. Computational complexity analysis

In this subsection, we will calculate the time complexity of different indicators when measuring network robustness,and highlight the superiority of our method by comparing the time complexity.

When calculatingHM,kM,andPM(kM)will be involved,and the calculation ofkMturns the most complicated, with the time complexity beingO(N·NM), whereNMrepresents the number of the 3rd-order motifs in the network. ForBG,the computational complexity mainly focuses onBe,the time complexity isO(N2·L), and the time complexity ofEGandDGareO(N2)andO(N3)respectively.

In the BA scale-free networks, only whenMis small,there isO(N·NM)

5. Conclusions and prospect

Motif, as a frequent interconnection pattern in the network, is used to measure the robustness of the network, and the decisive effect of the node itself and the interaction between the nodes on the robustness of the network is considered.Based on the 3rd-order motif,the entropy of node degree distribution is used to measure the robustness of the network under random attacks. At the same time, experiments on BA scale-free networks verify the effectiveness and superiority of our method, that is, the entropy of node degree distribution based on the motif can be used as a new index to measure network robustness,and the robustness of the network is directly proportional to it. In the future work, the robustness of directed networks and multilayer networks will be analyzed and measured based on motifs.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 62006169), the Youth Natural Science Foundation of Shanxi Province, China (Grant No. 201901D211304), the China Postdoctoral Science Foundation(Grant No.2021M692400),and the Science and Technology Innovation Projects of Universities in Shanxi Province,China(Grant No.2020L0021).