Oscillation properties of matter–wave bright solitons in harmonic potentials

Shu-Wen Guan(关淑文) Ling-Zheng Meng(孟令正) and Li-Chen Zhao(赵立臣)

1School of Physics,Northwest University,Xi’an 710127,China

2NSFC–SPTP Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

3Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

Keywords: matter–wave bright soliton,harmonic potential,oscillation period

1. Introduction

The motion of soliton pair were further discussed in a harmonic trap,[21–24]since multi-solitons can be prepared well in experiments and nonlinear interaction between solitons can also modify their oscillation behavior.[25]Quasi-particle model has been proposed to describe the motion of soliton pair well,[21,22]when the position shift induced by collision can be ignored. The position shift becomes larger with decreasing soliton’s collision speed.[26,27]Then it is essential to discuss the effects of position shift on oscillation behavior of soliton pair.

In this paper, we report that the effects of position shift can be addressed well by defining a characterized speed,with the aid of asymptotic analysis on related exact analytic soliton solutions in integrable cases.[28]We investigate oscillation periods of scalar bright solitons, vector incoherent solitons,[29]bright–bright solitons,[30–32]and dark–bright solitons[19,33]in a harmonic trap or anti-harmonic trap. When the soliton velocities increase, the two-soliton oscillations tend to be consistent with the results in Refs.[21,22]. The oscillation period can be used to distinguish the collision induced by inter- and intra-species interactions. Especially, a bright soliton cannot oscillate in a harmonic trap, when it is coupled with a dark soliton(without any trapping potentials).But it can oscillate in an anti-harmonic potential,and the oscillation behavior is explained by a quasi-particle theory. These results would inspire some experiments to observe the modified oscillation periods of soliton pair.

The paper is organized as follows. In Section 2, we investigate the oscillation of a bright soliton pair with coherent collision in a harmonic trap. We define a characterized speed to describe the modified oscillation period theoretically, with the aid of asymptotic analysis on related exact analytic soliton solutions in integrable cases. In Section 3,we study the oscillation periods of vector soliton pairs with incoherent collision.In Section 4,we study the oscillation periods of vector soliton pairs with both coherent and incoherent collision. The modified period differences are clarified for these three different types collisions,which can be used to distinguish the collision induced by inter-and intra-species interactions. In Section 5,we further investigate the oscillation of a dark–bright soliton in a harmonic trap or an anti-harmonic potential. The period of a dark–bright soliton pair is also obtained theoretically by the characterized speed. Finally,we make conclusion and discussion in Section 6.

2. The oscillation property of a bright soliton pair with coherent collision

whereAandvdenote the amplitude and velocity of a bright soliton,x0is the initial position of the soliton center. IfΩ ̸=0 andx0̸=0, a bright soliton can oscillate periodically under the effect of an external potential,which is formally identical with a particle.[4]The oscillation period isT0=2π/Ω,when the external potential vary slowly in the soliton scale. This character can be also explained by the dispersion relation of one soliton (see Appendix A). For a bright soliton pair, two solitons will collide with each other in a harmonic trap. It is known that a sudden position shift emerges after the collision process,[36]which surely affects the oscillation period.Quasi-particle model has been proposed to describe the motion of soliton pair well, when the position shift induced by collision can be ignored.[21,22,36]Then we would like to discuss the cases for which the position shift effects can not be ignored. We consider a general case for which a bright soliton pair is located in harmonic potential and the potential varies slowly within the soliton size scale,as shown in Fig.1(a). The initial state can be given as[37]

The initial positionx0can be used to vary the collision speed conveniently. According to asymptotic analysis of the twosoliton solution,[38]we obtain the position shift caused by soliton collision

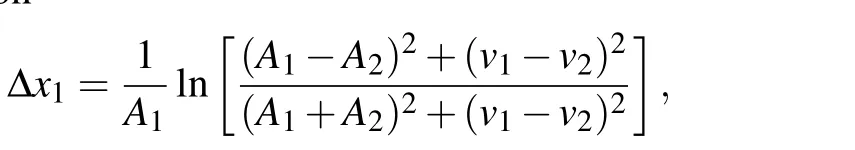
wherev1andv2denote the moving velocity of two solitons.We can see that the position shift increases with decreasing the relative speed. Therefore,we investigate the cases with the solitons’relative speed is small. As an example,we show one case numerically in Fig.1(b),for which the time is normalized with the periodT0. One can see that the soliton oscillation period is much less thanT0in this case , which means that it is indeed affected by the position shift effects.

Fig. 1. (a) The profile schematic diagram of the initial scalar soliton pair in a harmonic potential. The two solitons are symmetrically placed at the position ±x0 (x0 =10). (b) Oscillation of the soliton pair in the harmonic potential.The oscillation period is obviously less than that of only one bright soliton T0=2π/Ω. The harmonic frequency Ω =0.02,and other parameters A1=A2=2/2.

It indicates that the collision velocity is positively related to the solitons’initial positionx0,thus we can control the relative speed by placing solitons at different initial positions. Near the collision location(the harmonic trap center),the collision process of the two solitons can be approximately described by the two-soliton solutions with no external potential. Then the position shift induced by collision can be given by asymptotic analysis of the two-soliton solution.[38]The position shift should induce a time duration modification ∆T1,which can be described by

We find that numerical results agree well with our theoretical predictions when the relative speed is above the critical speed for tunneling behavior.[39]For example,we show the theoretical modification of the oscillation period vs different initial positions (red solid curves in Fig. 2) for the two bright solitons initially located symmetrically in the harmonic trap. The corresponding numerical simulation results are shown by the blue dashed curve in Fig.2. It is seen that our theoretical modification Eq.(5)can describe well the oscillation period of the soliton pair in a harmonic potential.

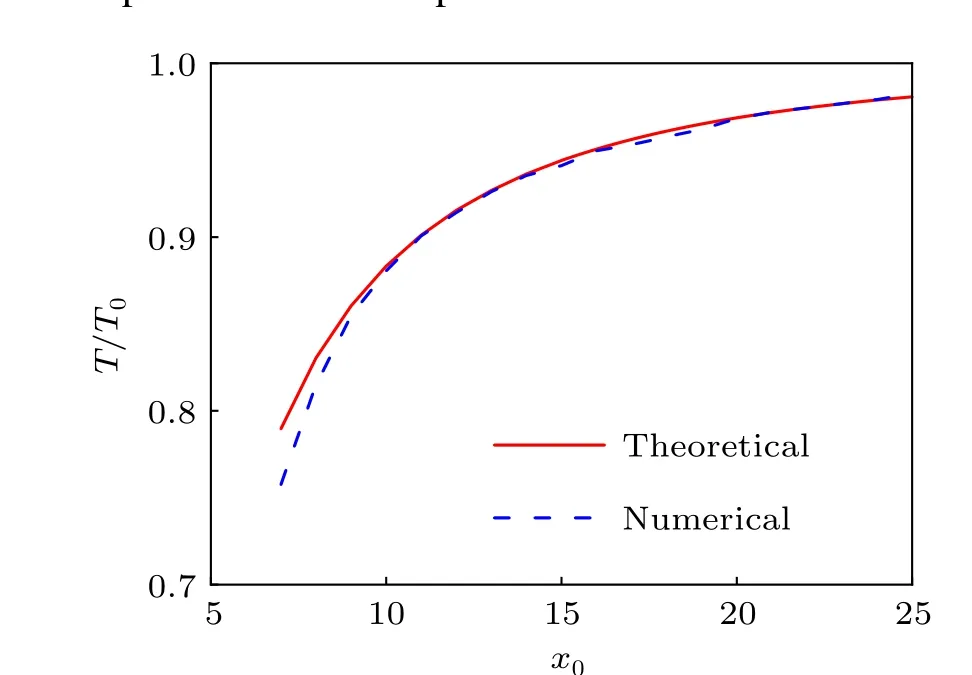
Fig.2. The oscillation periods of soliton pairs modified by collision interactions. The red solid and the blue dashed curves are given by our analytical results Eq.(5)and the numerical simulations. The two curves fit well with each other in a wide range of soliton speed. But they show a slight deviation when soliton speed is very small due to the tunneling effect. The period tends to T0 as the soliton speed increases.

It is known that the position shift tends to be zero with increasing the relative speeds between solitons,and the oscillation period will gradually tends toT0.[21,22,36]It should be noted that the effects of position shift can be still seen after many oscillation periods in the harmonic trap for large relative speed cases.[22]Interestingly, our results suggest that the period modification can occur obviously in only one oscillation period,when the relative speed is small.If we further decrease the relative speed(decrease the|x0|value),the oscillation periods will deviate from our theoretical predictions(see Fig.2).The deviation becomes much larger when the relative speed is lower. The deviation is induced the tunneling effect or resonant interaction between the two bright solitons,[39]which makes the quasi-particle picture can not hold anymore. The quantitative interpretation for the deviation is still need further discussion,which should be beyond the quasi-particle theory.

The effect of solitons collision in the identical component is demonstrated clearly in the above discussion. The collision can be seen as a coherent collision, due to that the interference pattern depends essentially on the relative phase between the two solitons. The collision between vector solitons such as bright–bright solitons, will involve both coherent and incoherent collision effects. Then we would like to discuss the oscillation behavior of bright–bright soliton pair in a harmonic trap. Recent studies on non-degenerate bright solitons[29,40,41]suggest that it is possible to investigate pure incoherent collision between solitons,for which the two solitons are placed in the two components separately (see Fig. 3(a)). The collision between solitons in different components are induced by intercomponent interactions, and there is no interference pattern during the collision process. The relative phase plays no role in the collision process,therefore the collision can be seen as incoherent collision. Then we investigate the oscillation property of vector soliton pairs with pure incoherent collision in follows.

3. The oscillation property of vector soliton pairs with incoherent collision

whereg=−1 denotes the nonlinear interaction strengths.V1(x) andV2(x) are the external potential for the two components separately. WhenV1(x) =V2(x) = 0, the CNLSE admits several vector soliton solutions, such as bright–bright solitons,[30–32]bright–dark solitons,[42]and the nondegenerate bright solitons.[29]These solutions can be used to give the initial conditions for observing soliton motion in weak external potentials. Firstly, we investigate the oscillation property of vector soliton pairs with pure incoherent collision in a harmonic trap, with the aid of non-degenerate bright solitons solution.[29]The external potential is also set asV1(x)=V2(x)=(1/2)Ω2x2,and the two soliton are placed symmetrically, as shown in Fig.3(a). The initial state can be given as

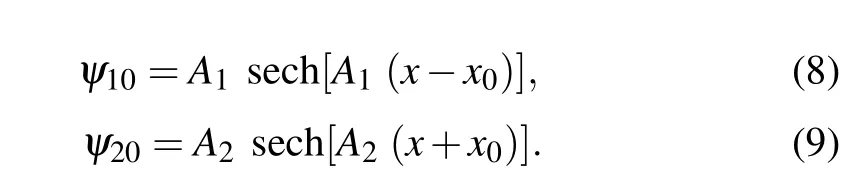
Fig. 3. (a) The profile schematic diagram of a vector soliton pair in a harmonic potential. A bright soliton is placed at x0 in the first component and the other is placed at −x0 in the second component. Panels(b)and(c)show the oscillation of the vector soliton pair. The incoherent collision effects also induce a position shift and make the oscillation of the vector soliton pair smaller than T0. The initial position x0 =10 and other parameters are A1=A2=/2.

We make numerical simulations with different velocities(blue dashed curve in Fig. 4) to verify this theoretical modification of the oscillation period(red solid curve in Fig.4).One can see that the theoretical predictions Eq.(11)are in good agreement with these numerical results,even if the collision speed is very small. Since there is no coherent interaction between solitons,the tunneling behavior is absent or the resonant interaction is much weaker for the two solitons even if the relative velocity is small, which enables the theoretical results holds more widely than the one for coherent collision case(see Fig.2).

“电声乐器和其他产品一样，也要经历一个从规模化到精工化的过程。鄌郚镇的乐器行业要想不被取代，必须下力气抓产品质量，打品牌，将产品做到极致，做出不可替代性，既要有形，也要有神。同时，我们还在研究旅游和电声产业的结合，搞吉他音乐节、电声产业论坛、音乐家村等，研发围绕电声产业的旅游商品，扩大鄌郚镇电声产业的影响力、提升旅游活力。”鄌郚镇镇长李克鹏说。目前，鄌郚镇已经规划建设了“昌乐县鄌郚乐器产业园”，按照国内一流标准，统一规划设计，统一服务管理，统一配套设施，并形成了乐器制作产业链，同时音乐节和吉他大赛的举办也吸引了数以万计的游客。

Fig.4.The oscillation periods of vector soliton pairs modified by incoherent collision interactions. The red solid and the blue dashed curves are given by our analytical results Eq.(11)and the numerical simulations. The numerical results are in good agreement with the theoretical results,since the tunneling effect is absent.

4. The oscillation property of vector soliton pairs with both coherent and incoherent collision

We consider the case which involves both coherent and incoherent collision effects. We put two vector bright soliton pair in harmonic potential,shown in Fig.5(a). The initial state is

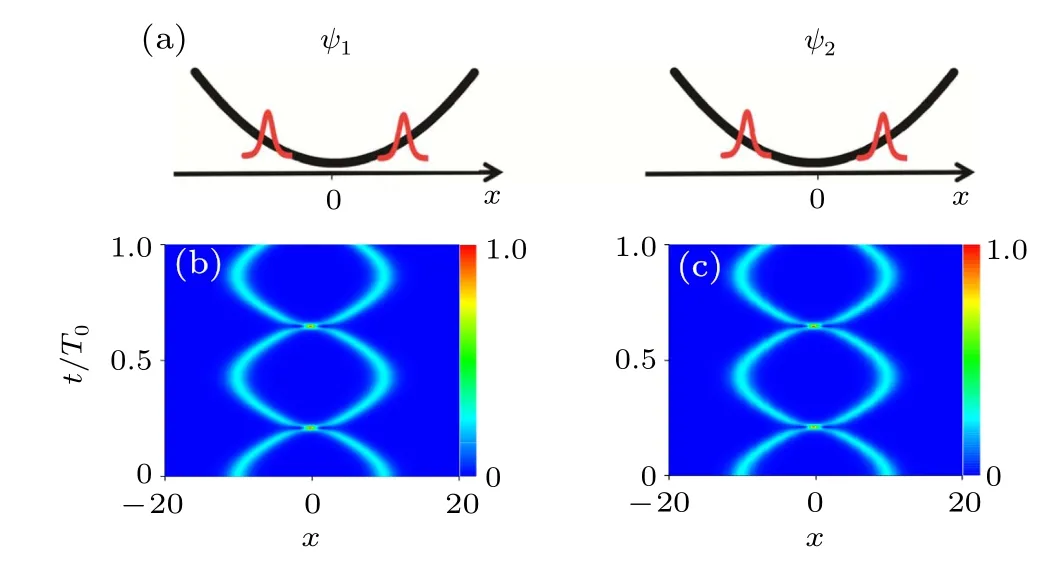
Fig. 5. (a) The profile schematic diagram of a vector bright–bright soliton pair in a harmonic potential. They are placed symmetrically at ±x0 positions. Panels (b) and (c) show the oscillation of the vector bright–bright soliton pair in the harmonic potentials of Ω =0.02. The oscillation period is also smaller than T0. The initial position x0=±10,and other parameters are Aj =/2.

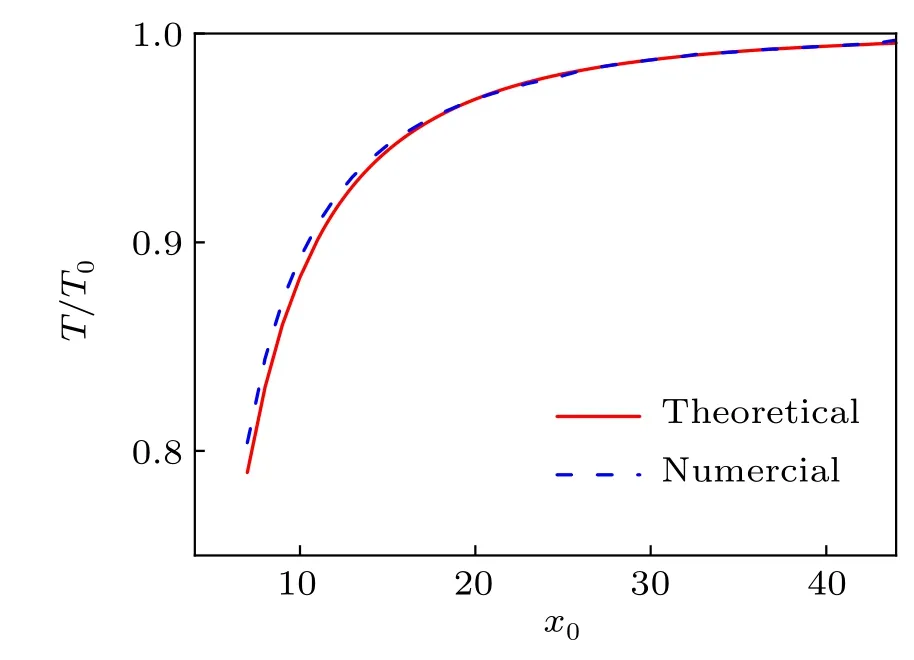
Fig. 6. The oscillation periods of vector bright–bright soliton pairs modified by both coherent and incoherent collisions. The red solid and the blue dashed curves are given by our theoretical results Eq.(14)and the numerical simulations.

Fig. 7. Comparison of oscillation periods under three different collisions(obtained by numerical simulations). The red solid(blue dashed)curve denotes that the solitons collide with only coherent (incoherent) interactions.The green dotted curve indicates that both of them exist. The coherent(incoherent)collision interactions have the greatest(least)modification on the oscillation period. When both two collision effects exist,the modification is determined by the interplay between them.

One can see that coherent (incoherent) collision have the greatest (least) modification on the oscillation period of matter–wave bright solitons. When the two collision effects both exist,the modification is determined by the interplay between them,which depends on the relative population ratio of two components. With increasing collision speed,these three oscillation periods tend to beT0. Based on these results, the oscillation period can be used to distinguish the coherent and incoherent collisions between solitons.

5. The oscillation property of dark–bright soliton pairs

The bright–dark solitons can also exist in the model Eq.(6)and Eq.(7)with attractive interaction between atoms.This could be used to investigate the effects of coupling with dark soliton on previously discussed bright soliton’s oscillation in the harmonic trap. However, this type of vector soliton is unstable due to the modulational instability. Then we can set interaction between atoms to be repulsive, namely,g=1, for which there are stable dark–bright solitons. WhenV1=0,V2=0 andg=1,the CNLSE Eq.(6)and Eq.(7)admits one dark–bright soliton solution as follows:

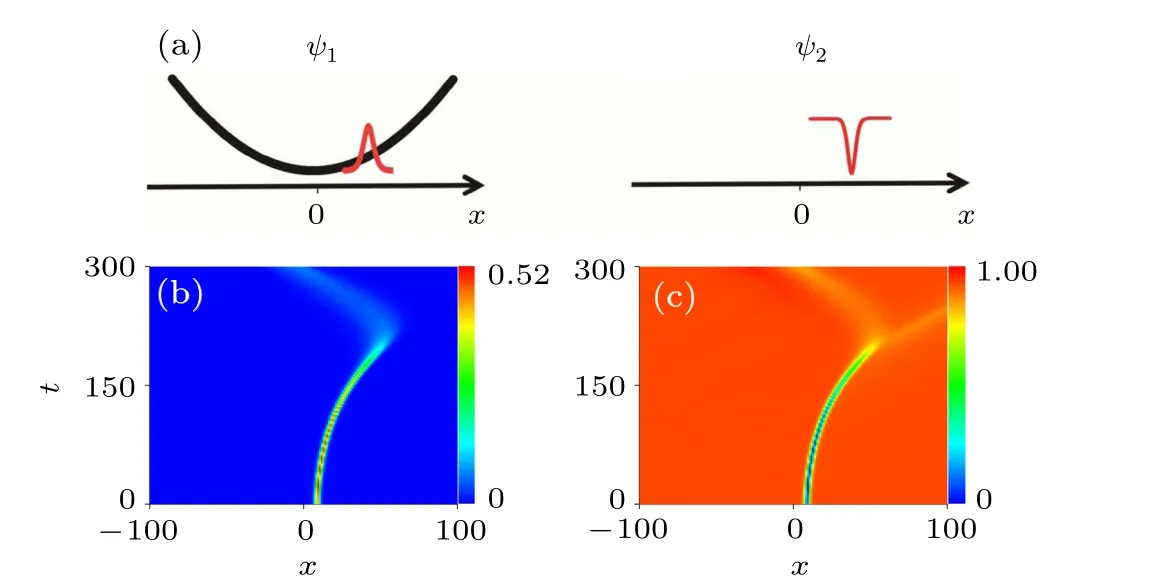
Fig.8. (a)The profile schematic diagram of a dark–bright soliton when the harmonic potential is applied to the bright soliton component. Panels (b)and (c) show that the dark–bright soliton cannot oscillate in this case. Instead, it firstly moves outwards and then diffused. Other parameters areΩ =0.02,x0=10,w=/2,and v=0.

As shown in Fig. 8(a), we put one bright soliton at the positionx=x0(x0>0)of the harmonic potential and a dark soliton at the same position. The initial states are given by the above dark–bright soliton solution. The density evolution of the dark–bright soliton is shown in Figs. 8(b) and 8(c). The result shows that a bright soliton cannot oscillate in a harmonic trap, when it is coupled with a dark soliton (without any trapping potentials). Strikingly, both bright soliton and dark soliton accelerates in the opposite direction to the force exerted throughV1and finally diffuses. This phenomenon is consistent with that the dark–bright soliton is driven out of the external trap.[19]In order to investigate a stable oscillation of dark–bright solitons, we change the harmonic potential to be an anti-harmonic potential

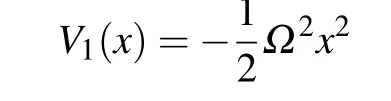
with keeping other conditions, which is shown in Fig. 9(a).The motion of dark–bright soliton is shown in Figs. 9(b) and 9(c), one can see that the dark–bright soliton can oscillate steadily with certain period in the anti-harmonic potential. Interestingly, the oscillation periodT′0is notT0=2π/Ωanymore (in contrast to the scalar bright soliton and the bright–bright soliton),which can be explained by soliton’s dispersion relation. The motion of the dark–bright soliton can be described well by a quasi-particle theory(see details in Appendix B), which is shown by white dashed curves in Figs. 9(b) and 9(c). Then we further discuss the effects of the position shift induced by solitons’ collision on the oscillation behavior of the dark–bright solitons.

Fig. 9. (a) The profile schematic diagram of a dark–bright soliton in antiharmonic potential. A bright soliton is placed at the position of x0 =10 in anti-harmonic potential and a dark soliton without trapping potential is placed at the same position. Panels (b) and (c) show that the dark–bright soliton can oscillate in an anti-harmonic potential of Ω =0.02. The moving trajectory of the soliton can be derived by a quasi-particle theory(white dashed curves). Other parameters are w=/2,and v=0.

We put two identical bright solitons into the potential at the positionx=±x0(x0>0)in the first component and two identical dark solitons at the positionx=±x0(x0>0)in the second component without potential (Fig. 10(a)). The initial states are given as[43]

Fig. 10. (a) The profile schematic diagram of a dark–bright soliton pair in anti-harmonic potential (Ω =0.02). Two solitons are placed at ±x0. The potential is only applied to the bright solion component. Panels(b)and(c)demonstrate that the oscillation period of the dark–bright soliton pair is modified by their collision,and the period is smaller than T′0. Other parameters are x0=10,w=√/2,and v=0.

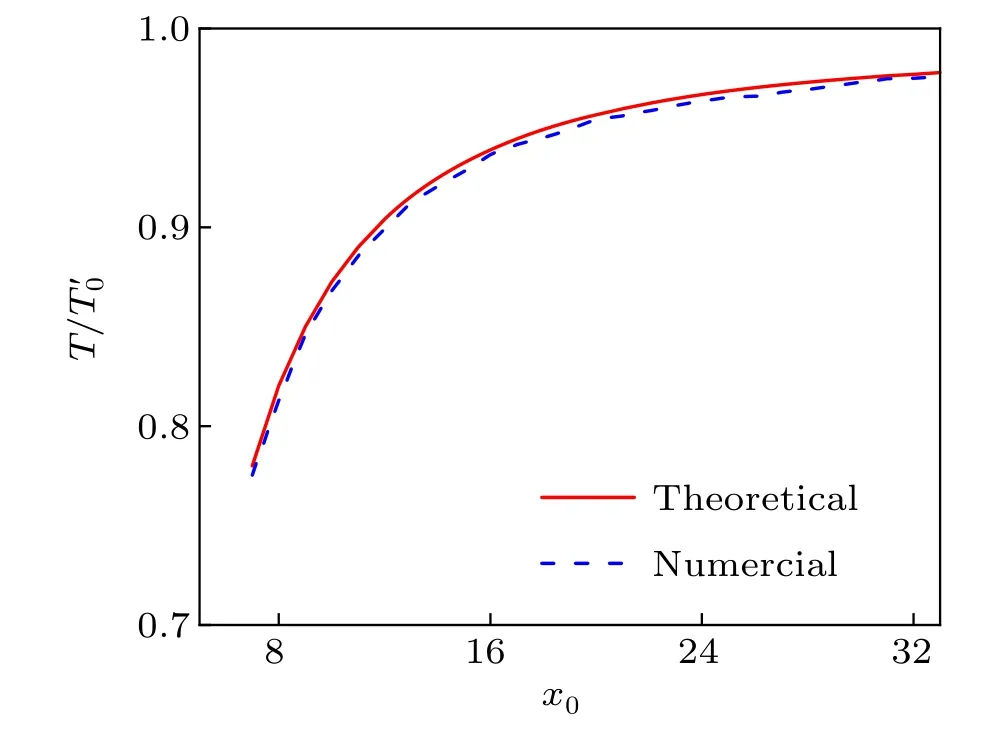
Fig.11. The oscillation periods of vector dark–bright soliton pairs modified by their collisions.The red solid and the blue dashed curves are given by our theoretical results Eq.(18)and the numerical simulations.

6. Discussion and conclusion

In summary, we investigated the oscillation period of matter–wave bright soliton pair in harmonic traps. The results show that position shift caused by collisions can change the oscillation period of solitons significantly when collision speed is low. With the aid of a characterized speed,we theoretically describe the modified oscillation periods induced by coherent collision, incoherent collision, and both of them. Moreover,we investigated the oscillation behavior of a bright soliton,when it is coupled with a dark soliton. Interestingly,the bright soliton can oscillate in an anti-harmonic potential rather than a harmonic trap. The motion of them can be described well by the dispersion relation of a dark–bright soliton. The position shift induced by collision are also discussed for the oscillation of dark–bright solitons.These results would deepen our understanding on the motion of bright solitons in harmonic traps,and could inspire some experiments to observe the modified oscillation periods of soliton pair.[36]The dispersion relation of solitons discussed here could be extended to other solitons of nonlinear systems.[45–50]

The above discussions focus on the modification of oscillation period when two solitons are placed symmetrically in a harmonic potential. It is still necessary to discuss the cases for which the two solitons are placed asymmetrically. However, our numerical simulation results show that solitons oscillations are no longer periodic in asymmetric cases. This is partly due to that complex energy exchange between solitons occurs during the collision interaction,which results in different positions for each collision.

Deviatingtto both hands, we can obtain the acceleration of dark–bright soliton in anti-harmonic potential, when the soliton speedv →0. Thus,we obtain the theoretical trajectory of a dark–bright soliton which is shown in Figs.9(b)and 9(c)as white dashed curves.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.12022513,11775176,11947301,and 12047502)and the Major Basic Research Program of the Natural Science of Foundation of Shaanxi Province, China(Grant Nos.2018KJXX-094 and 2017KCT-12).