基于遗传算法与模糊分数阶PID 的钢结构损伤检测机器人姿态控制①

艾青林 蒋锦涛 刘刚江 宋国正 徐巧宁

（浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室 杭州310023）

0 引言

近年来,全国各地各种大型复杂建筑不断新增,其中钢结构被广泛应用于体育场、桥梁和铁路交通设施等[1]。然而有些钢结构建筑由于施工问题和多年超负荷运营可能造成各种安全事故。因此对大型钢结构建筑进行损伤检测和即时维护显得尤为重要。目前钢结构建构损伤检测方法中,应用最为广泛的是传统数据采集方法,但是过程繁杂且效率低,存在着检测区域盲点和检测内容不全面等问题。

本文采用了一种柔性移动机器人对钢结构进行探伤,该机器人使用柔性钢带连接前后车体,并采用磁力轮吸附在钢结构建筑上。该机器人可以在钢结构建筑上翻越障碍,自主运动到目标位置进行定点损伤检测[2]。柔性机器人前后车体缺少刚性约束,属于非完整约束的非线性系统,其运动学与动力学建模非常复杂,难以对其运动姿态进行实时高精度控制。

针对外形细长、多模块的水下滑翔蛇形机器人,文献[3]基于动量定理、动量矩定理以及递推牛顿-欧拉法,建立了机器人滑翔运动和蛇形游动的动力学模型。文献[4]提出了一种基于非线性滑模控制（JSTDE）的自适应控制技术,适用于动力学不确定的外骨骼机器人。但是滑模控制使得系统在滑模面附近高速切换,将会产生高频抖振问题。文献[5]采用改进近似法设计了分数阶比例积分微分（proportional integral derivative,PID）控制器,实现对四旋翼飞行器的姿态控制和位置跟踪,但在分数阶PID 阶次整定上采用了低效、低精度的手动调整。

本文将柔性机器人前后车体视为一级倒立摆[6],建立柔性机器人整体动力学模型,采用基于改进遗传算法与模糊分数阶PID 控制方法[7],对分数阶PID 阶次与参数进行整定优化,实现机器人运动姿态高精度实时控制。最后通过柔性机器人姿态控制仿真实验,验证模糊分数阶PID 控制器对柔性机器人运动姿态控制的高效性和稳定性。

1 柔性机器人动力学建模

柔性机器人结构如图1 所示,首先分析其各个部分的运动和受力状态,建立车轮、车体及柔性钢带的数学方程,通过对方程的化简和整合,最终得出柔性机器人的整体动力学模型。

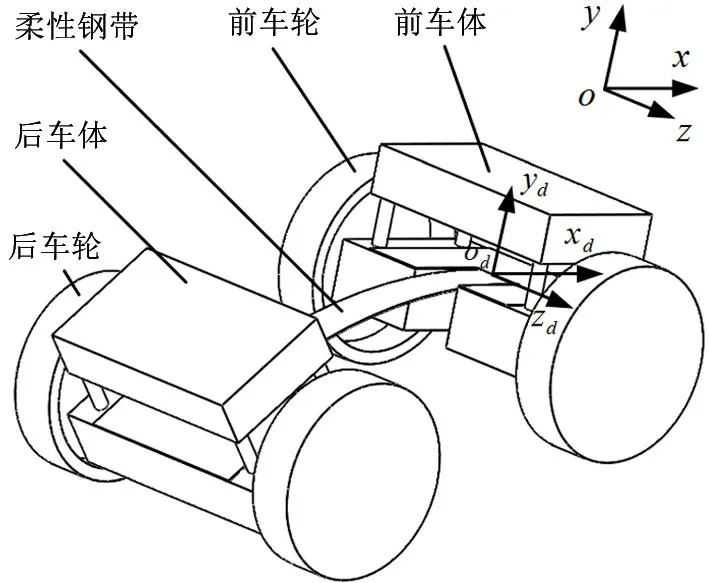
图1 柔性机器人示意图

为了便于分析和计算,对柔性机器人做以下假设:车身车轮等视为理想刚体,车轮保持纯滚动运动而无滑动,忽略机器人各部件之间的摩擦力。由于柔性钢带对前后车体的运动束缚,柔性机器人的前后车体保持相对称的运动状态,即俯仰角相同。由于本文是对柔性机器人的俯仰角进行控制,因此忽略水平面上的偏航角所带来的干扰,即设定左右车轮无速度差。

1.1 柔性钢带动力学分析

如图2 所示,将大挠度变形的柔性钢带简化为由弹簧、阻尼器、滑块和连接杆组成的等效结构。柔性钢带的形变-受力特性与弹簧阻尼类似,其关系与等效结构的相互对应。

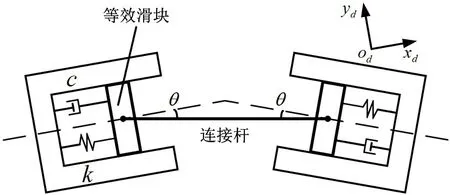
图2 钢带等效结构模型

等效结构的受力情况如图3 所示,其中点P为等效滑块的初始位置,点M、M′为左右车轮的对称中心,点N、N′为等效滑块的瞬时位置。|MM′|=d表示前后车轮之间的实时距离。|NN′|=D表示连接杆的长度,即柔性钢带的原始长度。|PN |=XD表示等效滑块位移。对等效滑块进行受力分析:

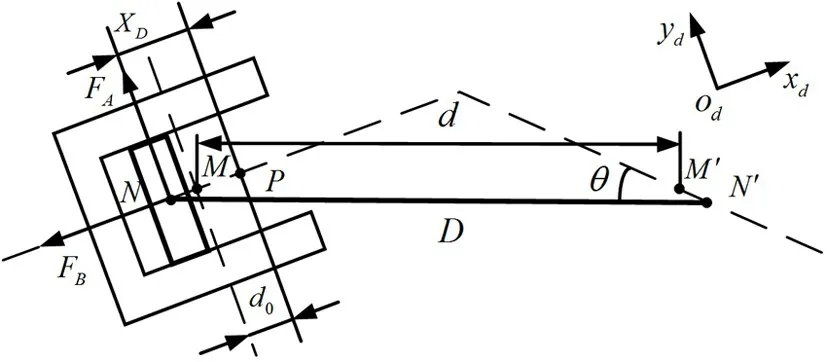
图3 等效结构受力分析图

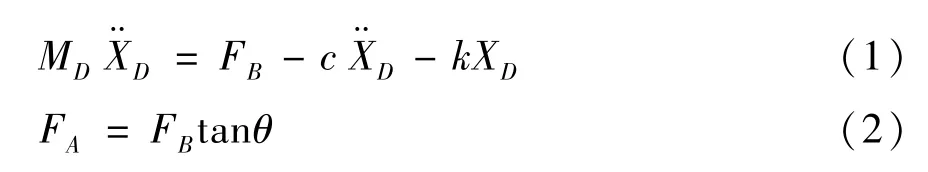
式中,MD为等效滑块质量,XD为等效滑块位移,FA为连接杆对车体的垂直分力,FB为连接杆对车体的水平分力,c为阻尼系数,k为弹簧系数,θ为车体俯仰角。

柔性机器人前后车轮的相对距离:

式中,d为前后车轮距离,XR1为后车轮水平位移,XR2为前车轮水平位移,α为斜坡轨道倾斜角度。

等效滑块的位移:

式中,D为钢带原长;d0为等效滑块初始位置与车轮对称中心的偏移量,默认为0。

通过式（1）、（3）、（4）,可得:

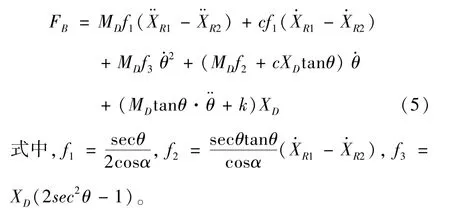
1.2 车轮动力学分析

图4 为后车轮的瞬时受力图,其中点C1为车轮质心。对柔性机器人的车轮进行受力分析,在水平与竖直方向上为

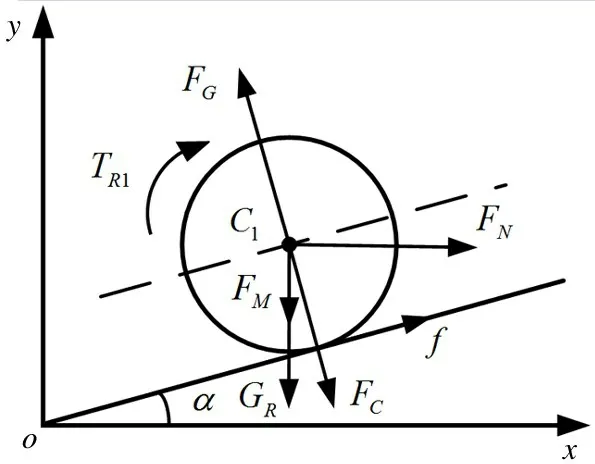
图4 车轮受力分析图

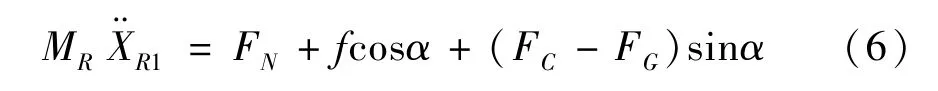
式中,MR为车轮质量,FN为后车体对车轮的水平分力,f为车轮摩擦力,FC为磁力,FG为支持力。

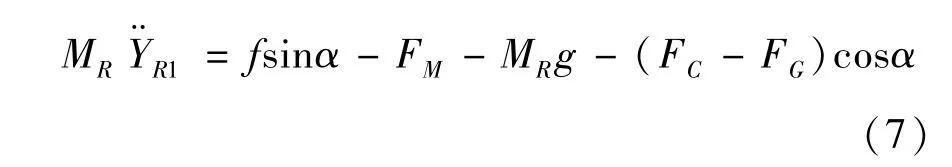
式中,YR1为后车轮竖直位移,FM为后车体对车轮的竖直分力,g为重力加速度。

车轮转矩:

式中,JR为车轮转动惯量,θR1为后车轮转动角度,TR1为后车轮转矩,R为车轮半径。

柔性机器人运动轨迹受到斜坡轨道的限制,由此可得到车轮水平、垂直加速度之间的关系:

车轮磁铁的磁力使得车轮吸附在轨道上,则在垂直于轨道的方向上车轮保持受力平衡:

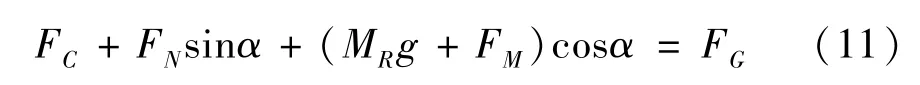
车轮位移加速度和转动角加速度的关系为

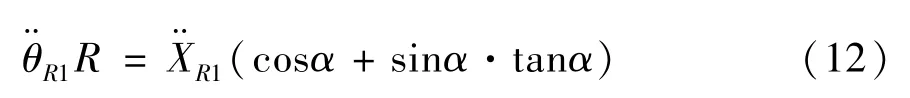
1.3 车体动力学分析

图5 为柔性机器人后车体的瞬时受力图,其中点C1为车轮质心,点C2为车体质心,|C1C2|=L。F′N、F′M、T′R1分别是图4 中FN、FM、TR1的反作用力、力矩,数值大小相同,作用方向相反。分析可得后车体在水平和竖直方向上的受力方程。

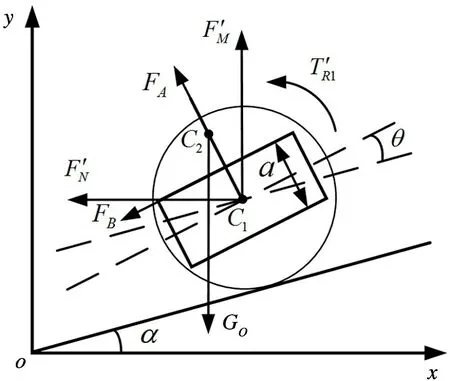
图5 车体受力分析图

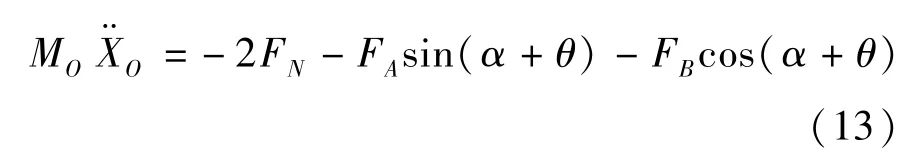
式中,MO为车体质量,XO为后车体质心水平位移。

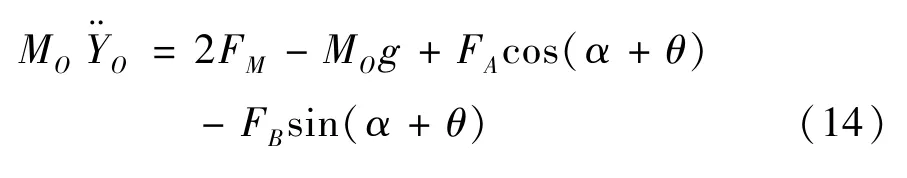
式中,YO为后车体质心竖直位移。

车体转矩:

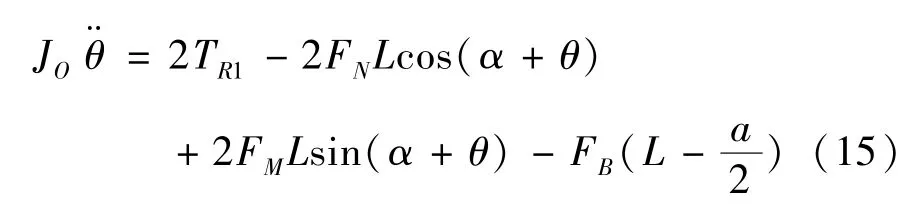
式中,JO为车体转动惯量,L为车体与车轮质心距离,a为车体高度。

车体质心与车轮质心位置坐标关系如下:

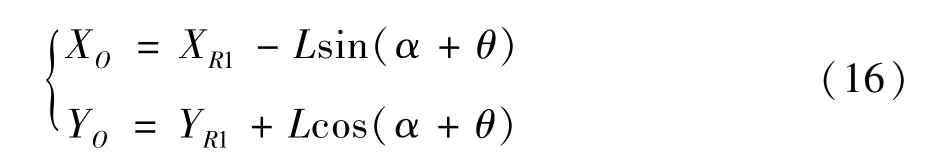
1.4 柔性机器人整体动力学分析

将前文中车轮、车体和等效结构三者公式进行化简整理,即可得到柔性机器人整体的模型。

将式（9）、（12）代入式（8）后,化简得到摩擦力f的表达式:

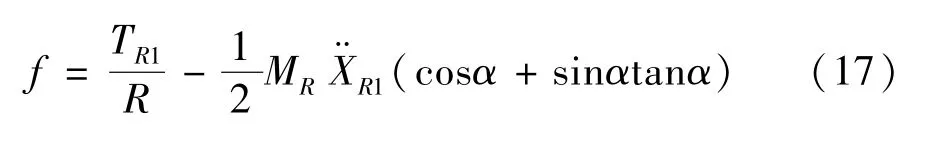
将式（11）带入式（6）,化简得:

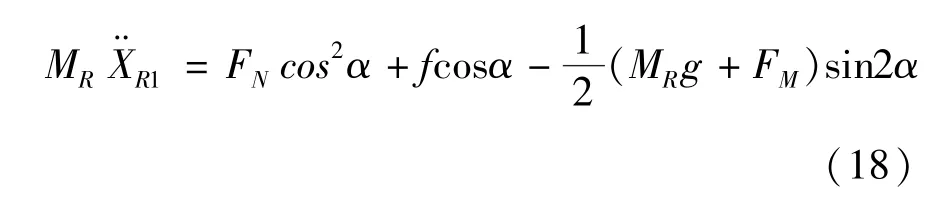
结合式（15）、（18）可获得柔性机器人后车体的动力学方程为

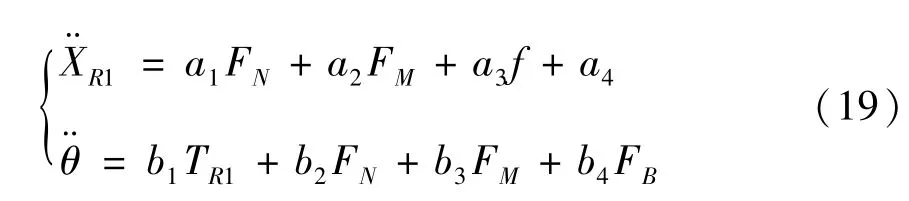
式中,ai、bi（i=4） 分别是已知表达式,FB、f已在前文中求出其表达式。FN、FM可以通过将式（2）、（10）、（16）代入式（13）、（14）后计算得到。

前后车体保持对称的状态,因此前车体动力学方程与后车体动力学方程格式一致,区别在于车体质心位移以及电机产生的力矩。将前后车体的两组方程结合,最终可以得到输入力矩（TR1、TR2）、俯仰角（θ）和前后车体位移（XR1、XR2） 三者之间高度耦合的关系方程组。

2 基于遗传算法与模糊分数阶PID 设计

柔性机器人属于高度非线性与不确定性系统,存在欠驱动。在运动姿态控制上如果要应用PID 控制等传统方法[8],须先对其动力学方程做解耦处理。而且传统控制方法精度不高,抵抗不确定干扰和降抖振能力差。因此本文选择具有自调节特性的模糊控制方法,并将其与分数阶PID（fractional-order PID,FOPID）控制相结合。同时使用改进遗传算法,对分数阶PID 阶次进行最优化整定,进一步提高整个控制系统的鲁棒性。

2.1 分数阶PID 控制器

实际应用中,传统PID 控制器需要凭借经验和固定公式来选择合适的比例、积分、微分系数,对复杂模型的控制效果不佳。PID 控制方法的控制规律可以描述为

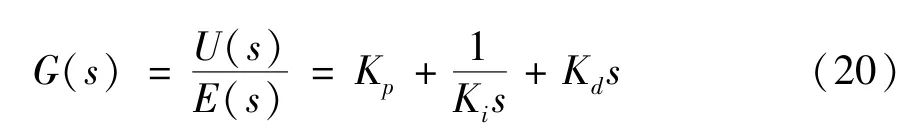
式中,Kp为比例系数,Ki为积分系数,Kd为微分系数,e（t） 为系统误差。

分数阶PID 控制是整数阶PID 控制器的一个拓展,也是现代控制理论中一个逐渐被人们广泛应用的分支[9]。相比于整数阶PID 控制器的Kp、Ki、Kd3 个控制参数,还增加了积分阶次λ和微分阶次μ。分数阶微积分的基本操作算子为,其表达式如式（21）所示[10]。

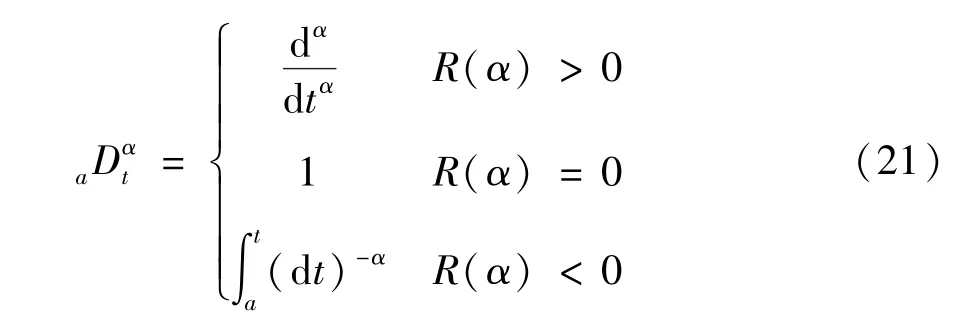
式中,a和t分别是分数阶微积分操作算子的上下限,α为微分（α >0） 的阶次或者积分（α <0） 的阶次。

分数阶PID 控制器的传递函数为

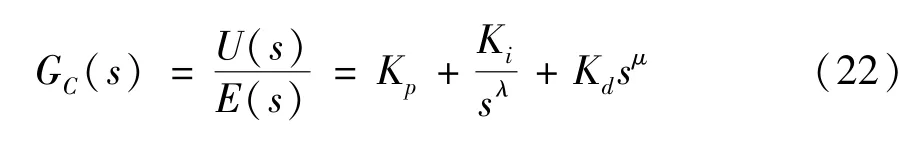
式中,λ是积分阶次,μ是微分阶次,e（t）=r（t）-y（t） 是控制器输入,u（t） 是控制器输出。

分数阶PID 控制器的2 个参数λ和μ可以是0到1 之间的任意值。通过式（20）和（22）的对比可以看出,分数阶PID 控制器要比传统整数阶PID 控制器更加灵活,控制更加精确。最常用的分数阶微积分定义分别是Riemann-Liouville（RL） 定义和Grunwald-Letnikov（GL）定义。本文选用更加适合数值计算的GL 定义[11]:

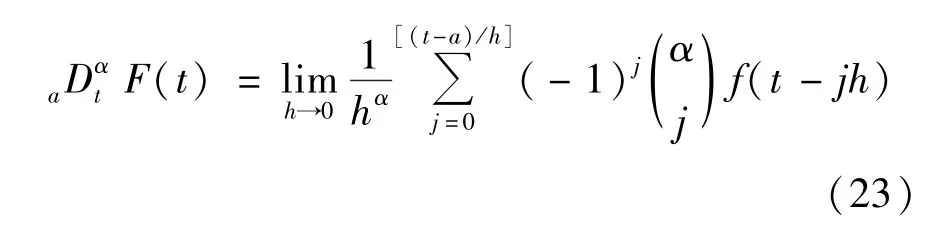
式中,α是微积分的阶数,h是假定的非常小的步长,

用以下的离散形式来表达分数阶微积分算子:

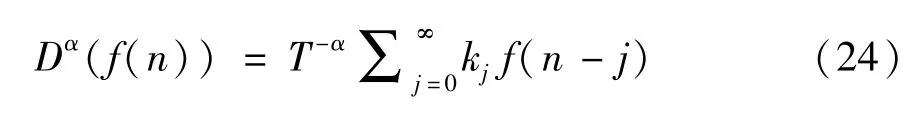
式中,T=1/h为采样时间;kj为二项式系数,其定义为k0=1,

由式（24）可知,要实现分数阶微分积分算子,需要计算无穷大的系数。但这在实际的应用中无法实现,因此要对分数阶微积分算子进行离散化计算或者近似计算处理。在式（24）中求和计算分数阶算子时,只使用其中一部分值来近似化解。因此可以将式（24）简化为

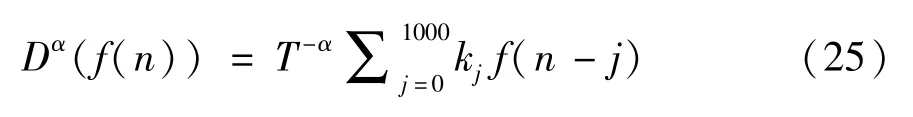
2.2 模糊控制器

由于柔性机器人是高度非线性系统,纯粹的分数阶PID 控制器难以实现理想的控制效果。因此,本文在分数阶PID 的基础上加入模糊控制,对分数阶PID 的比例、积分、微分系数进行动态调整[12],提高控制器的自适应能力。

模糊分数阶PID 控制器（fractional order fuzzy PID controller,FOFPID）以误差E和误差的变化率EC作为输入变量,以ΔKp、ΔKi、ΔKd3 个参数作为输出变量。设定2 个输入变量的论域为{-6 ≤IN≤6,IN∈N},3 个输出变量论域为{-10 ≤OUT≤10,OUT∈N}。输入、输出变量的语言值模糊子集为{负大、负中、负小、零、正小、正中、正大},记作{NB、NM、NS、Z、PS、PM、PB}。选用三角形的隶属度函数,将输入输出值映射到合适的区域内。综上所述,模糊分数阶PID 控制器可表示为

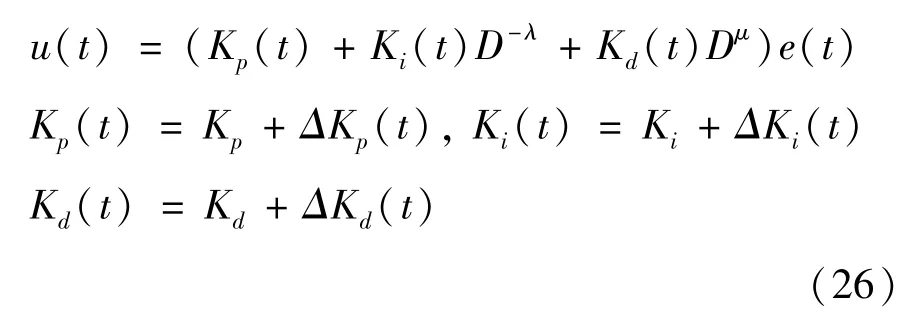
由上述公式可以得到模糊分数阶PID 控制器的结构,如图6 所示。

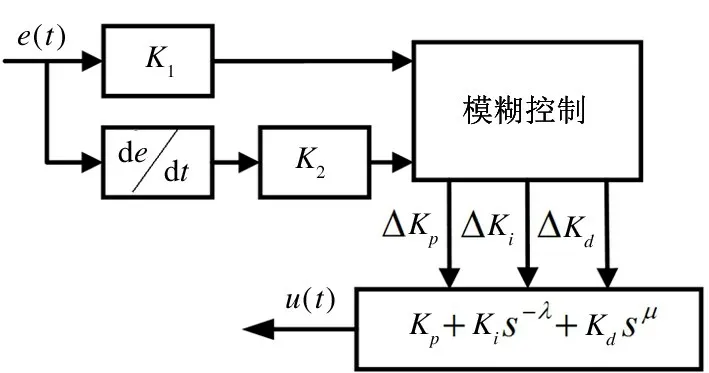
图6 模糊分数阶PID 控制器

2.3 改进遗传算法

模糊控制的加入使控制器的控制参数从3 个增加到5 个,导致手动调节控制参数的方法显得繁琐且难以满足各项控制指标,需要引入更高效的参数优化算法。

本文选用遗传算法（genetic algorithms,GA）实现对分数阶PID 阶次的整定,控制器如图7 所示。遗传算法输出λ、μ参数给分数阶PID,分数阶PID输出控制力矩给被控模型。完成参数整定后,柔性机器人运动姿态控制仿真中便不再使用遗传算法。

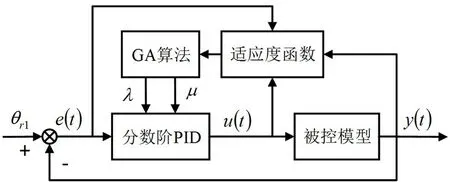
图7 遗传算法整定参数

遗传算法中最为关键的是适应度函数以及3 个遗传算子（选择、交叉、变异）的确定[13]。

适应度函数为Fitness=1/（F+A）,在控制过程中如果没有出现超调,则最小目标函数F使用式（27）;反之则使用式（28）,采用惩罚功能来减少超调的出现[14]。

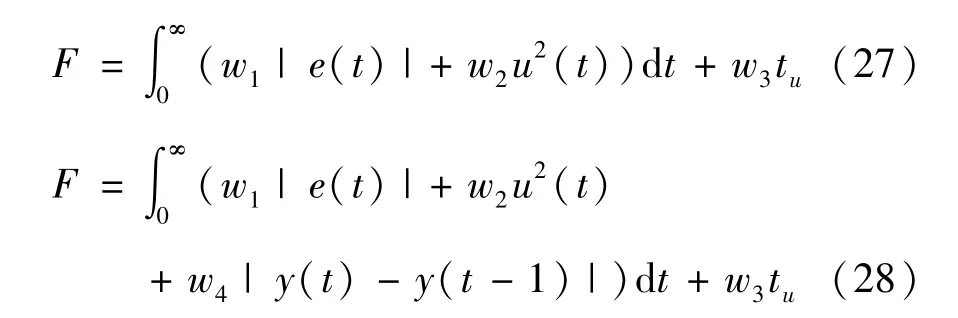
式中,e（t） 是系统误差,u（t） 是控制器输出,w1、w2、w3、w4是加权值,tu是上升时间。

交叉概率决定遗传算法的全局搜索能力,变异概率决定算法的局部搜索能力,影响种群更新速度以及是否会陷入局部最优解[15]。传统算法交叉和变异概率是常数,且难以调整到最佳值。本文采用自适应遗传算法（adaptive GA,AGA）,交叉和变异概率公式如下所示。

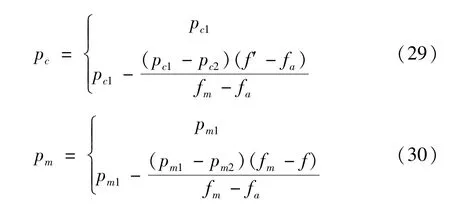
式中,pc为交叉概率,pc1、pc2为最大、最小交叉概率,pm为变异概率,pm1、pm2为最大、最小变异概率,f为个体的适应度值,fa为每一代种群的平均适应度值,fm为种群中最大的适应度值,f′为将要进行交叉的2 个个体中较大的适应度值。

改进遗传算法在仿真早期有着较强的全局搜索能力,在仿真后期局部搜索能力得到提高,能够更精确地迭代出最优解。

2.4 柔性机器人整体控制器

通过2 个相同的模糊分数阶PID 控制器,对柔性机器人的前后车体的俯仰角进行控制。根据柔性机器人动力学模型输出的俯仰角θ1,控制器实时调整电机的力矩TR1输出给后车轮,形成闭环控制。柔性机器人的前车体俯仰角控制过程与后车体的相似,整体控制器如图8 所示。

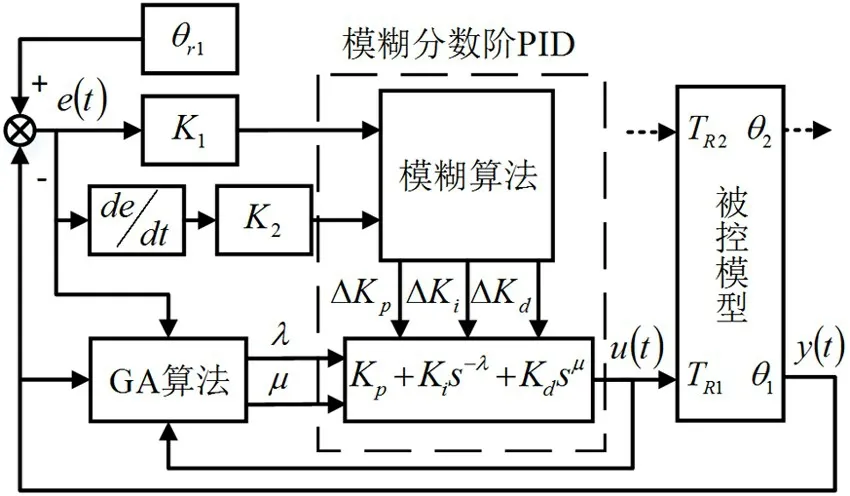
图8 柔性机器人控制器

3 柔性机器人姿态控制仿真实验

采用仿真软件Matlab/Simulink 对基于改进遗传算法与模糊分数阶PID 的柔性机器人姿态控制进行仿真研究。柔性机器人的各项参数值为:MO=0.342 kg,MR=0.11 kg,MD=0.005 kg,k=25 N/m,c=0.8 N·s/m,J0=2.96×10-4kg·m2,R=0.04 m,L=0.017 m,a=0.025 m,D=0.15 m。

3.1 基于遗传算法的分数阶PID 阶次整定

通过改进遗传算法的迭代运算,对分数阶PID的阶次λ、μ进行参数整定。设定初始种群的大小为30,总共进行50 次的迭代,种群选择率为40%,杂交概率为60%～80%,变异概率为0.1%～10%。目标函数的各项系数为w1=0.999,w2=0.001,w3=2,w4=100。

图9 是整定分数阶PID 阶次λ、μ时,每一次迭代中适应度最高的一组值。在20 °斜坡轨道的环境中,分数阶PID 阶次最终整定为λ=0.8859、μ=0.5366。在求解阶次μ时,改进遗传算法在仿真前期快速找到近似解0.7994,同时并没有陷入“早熟”,进一步地迭代出新的参数值0.5372。在仿真后期,算法具备高效的局部搜索能力,对参数值进行细微调整以得到最优解0.5366。阶次λ同样经历多次迭代更新,最终得到最优值。

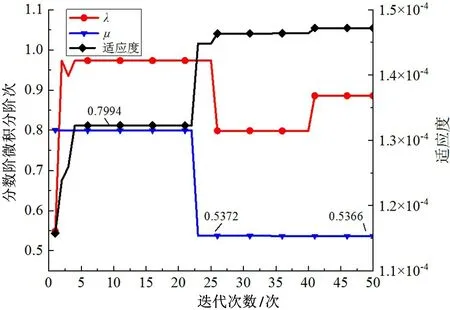
图9 分数阶PID 阶次整定图

从适应度曲线可以看到,每一次的算法迭代,最优解的适应度数值都没有下降,并且在仿真后期也有小幅提高。可见改进后的遗传算法,在保护高适应度个体的同时,又能够有效地避免“早熟”,使参数值尽可能地趋近最优解。

3.2 不同工况模糊分数阶PID 控制对比

选择在不同工况下进行运动仿真,来验证模糊分数阶PID 控制器对于柔性机器人运动姿态的控制效果。

柔性机器人在水平面上运动,维持俯仰角分别为10 °、20 °、30 °,控制效果见图10。在维持较大俯仰角的情况下仿真前期产生较大超调量,但是模糊分数阶PID 控制器能快速地调整被控模型的运动姿态,减小超调量,实现预期控制目标。在仿真后期,保持良好的稳定性和极低的稳态误差,未产生明显的抖振。

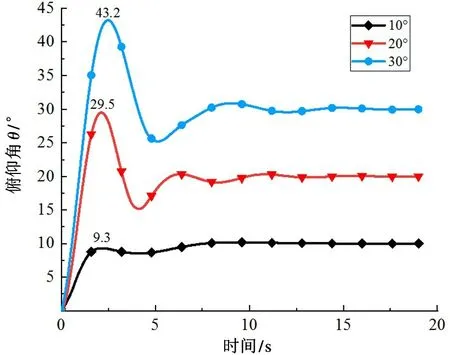
图10 水平面俯仰角控制图

柔性机器人维持15 °的俯仰角,在倾斜角分别为10 °、20 °、30 °的斜坡上运动,控制效果见图11。从图中可以看出,在斜坡轨道上运动,被控模型在仿真初期产生的超调量比水平面仿真时大幅减小。仿真后期的稳态误差有所增大,但维持在0.2 °以内,满足控制要求。

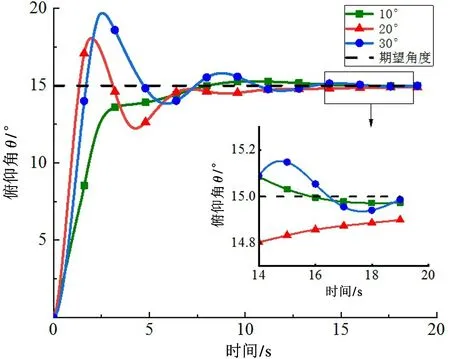
图11 不同坡度俯仰角控制图

综上所述,在较平缓的轨道上维持较小俯仰角运动时,模糊分数阶PID 控制器的控制效果良好,超调量低,调节时间短且稳态误差小。在坡度较大的轨道上维持较大俯仰角运动时,被控模型在仿真前期出现较大的超调量,但仍保持高效的调节速度,同时抖振得到了有效的抑制。

3.3 不同控制方法对比

为了进一步说明模糊分数阶PID 控制器对于柔性机器人的运动姿态控制效果良好,选择了多个控制算法进行对比。在20 °的斜坡轨道上,使用普通PID 控制器、模糊PID 控制器（FPID）以及模糊分数阶PID 控制器（FOFPID）这3 种控制方法来控制柔性机器人,仿真结果如图12 所示。

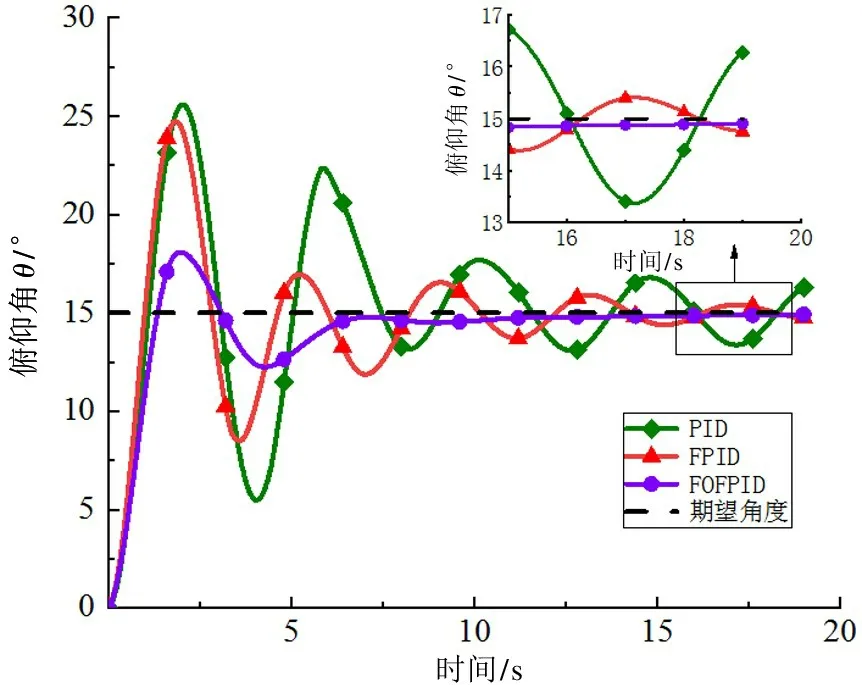
图12 不同控制器俯仰角控制图

图12 中,柔性机器人在模糊分数阶PID 控制器的控制下,在1.09 s 首次达到预期运动姿态角度,在6.02 s 达到运动稳态,最大超调量仅为20.46%。使用普通PID 控制器,系统超调量极大,长时间无法达到稳定控制,且存在明显的大幅度抖振。使用模糊PID 控制器,同样存在超调量过大的问题,虽然控制后期逐渐实现了稳定控制,但调节时间过长,不利于柔性机器人的实时控制。模糊分数阶PID 控制器控制效果明显优于另两种控制器,能快速达到预期控制状态,且整个控制器输出平滑稳定、后期的稳态误差小、抖振极弱。

通过表1 对比分析也可看出,模糊分数阶PID控制器在调节时间、超调量和稳态误差等指标上有着更佳的控制性能。

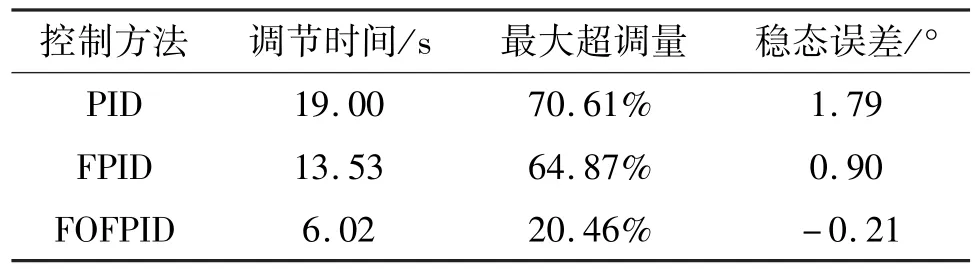
表1 不同控制器的控制指标

图13 是3 种控制器在20 °的斜坡轨道上,维持被控模型15 °俯仰角时,被控模型的俯仰角角速度变化曲线图。模糊分数阶PID 控制器所产生的最大角速度为14.01 °/s,远小于另外2 种控制器。同时被控模型的俯仰角角速度变化平缓平滑,在仿真后期趋近0。在另外2 种控制器的控制下,被控模型的俯仰角角速度波动较大,存在多处突变点,且存在明显抖振。

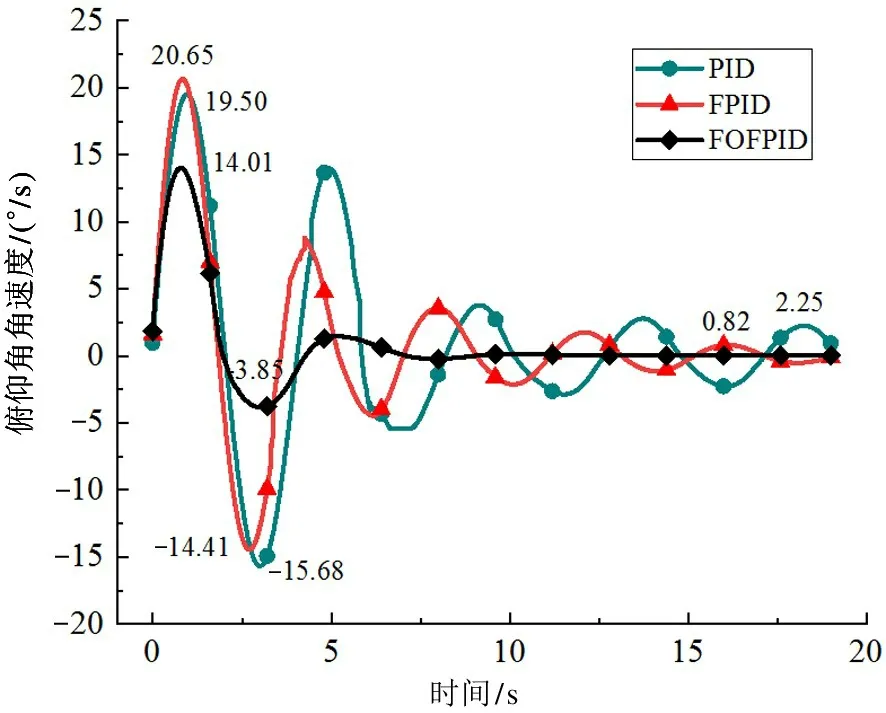
图13 不同控制器俯仰角角速度

图14、15 是3 种控制器在20 °的斜坡轨道上,维持被控模型15 °俯仰角时,被控模型俯仰角的角加速度变化曲线图。

如图14 所示,在模糊分数阶PID 控制器控制下,被控模型启动时存在一个较大的角加速度,在趋近目标角度时产生一段小幅度的抖振,随后抖振被抑制,角加速度曲线中后期整体平滑且数值趋近于0。

图14 FOFPID 控制器俯仰角角加速度

图15 表示模糊PID 控制器与普通PID 控制器的角加速度控制效果图。其中,在模糊PID 控制器控制下,不仅启动时有一个较大的角加速度,还存在多处突变点,最大达到869.15 °/s2。在普通PID 控制器的控制下,存在一段较长时间的抖振,有多处角加速度的突变,最大达到994.60 °/s2。在实际的应用中,图15 中出现的超大角加速度突变值,会导致柔性机器人整体的运动失稳。

图15 PID、FPID 控制器俯仰角角加速度

为模拟现实环境,在控制系统中加入一个外部干扰,即在仿真运行19 s 时增加来自外部的阶跃信号。如图16 所示,被控模型的俯仰角在19 s 时突变成了20 °。对于外部环境的干扰,模糊分数阶PID控制器的控制效果仍优于其他控制器,能够快速地调整俯仰角,抗干扰性更强。

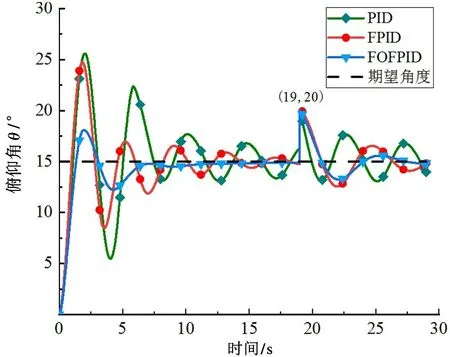
图16 扰动下不同控制器俯仰角控制图

4 结论

（1） 建立了柔性机器人车体、车轮及柔性钢带动力学模型,并整合以上公式得到柔性机器人整体动力学模型。

（2） 提出一种基于遗传算法与模糊分数阶PID控制方法,对柔性机器人运动姿态进行控制,提高系统的自适应性,加快了整个控制系统的收敛,并有效地抑制了抖振。

（3） 基于模糊分数阶PID 控制器,仿真实验研究不同工况与控制器对柔性机器人姿态角控制性能的影响。结果表明,模糊分数阶PID 能够实时控制柔性机器人运动姿态角并有效抑制抖振,具有较快的响应速度和良好的稳定性。

在未来工作中将会研究高速运动中如何实现柔性机器人运动俯仰角的快速调整和降抖振,以满足机器人在复杂钢结构环境中的越障需求。