一类非参数不确定运动系统的自适应空间重复学习控制①

陈 强 胡如海 胡 轶

（浙江工业大学信息工程学院 杭州310023）

0 引言

重复学习控制能够利用上一周期运行的数据修正当前周期的控制输入,实现周期轨迹的零误差跟踪或周期不确定动态的完全抑制[1-5]。与迭代学习控制不同之处在于,重复学习控制适用于连续无限时间区间上的周期轨迹跟踪,且无需在每次任务开始前进行初始定位。经典重复学习控制理论通常也被称为重复控制,主要思路是通过在频域内应用内模原理构造周期为T的任意周期信号内模,实现对周期信号的完全跟踪[6-10]。与已有的非线性反馈控制方法相比,重复控制在跟踪周期性期望轨迹和补偿周期不确定动态时能够获得更高的控制精度。

近年来,基于李雅普诺夫方法的自适应重复学习控制被提出,并被广泛用于处理不确定系统的高精度轨迹跟踪问题[11-20]。文献[14]针对一类时变参数不确定非线性系统,提出一种周期自适应学习控制方法,并基于李雅普诺夫方法证明闭环系统的全局渐近稳定性。文献[15]针对非参数不确定非线性系统的周期性轨迹跟踪问题,提出一种重复学习控制方法并证明该方法的有效性。文献[16]针对机械臂动态模型,讨论了部分饱和以及全饱和学习律的重复学习控制器设计方法。文献[17]针对一类时不变非线性系统的控制问题,提出线性输出反馈重复学习控制方法,并基于李雅普诺夫定理证明该方法的有效性。文献[18]针对分数阶系统,考虑非参数不确定外部扰动等问题,设计自适应重复学习同步控制器,实现了主系统和从系统的完全同步。文献[19]针对一类部分反馈线性化的非线性系统,提出一种状态反馈重复学习控制方法,保证系统跟踪误差渐近收敛到零。文献[20]针对欠驱动海上吊杆起重机系统,提出一种自适应重复学习控制方法,实现有效载荷定位和摆幅消除的双重控制目标。

上述重复学习控制方法大多针对系统执行时间域上的重复任务,而许多实际运动系统,如永磁同步电机、绕地球轨道旋转的卫星等,往往执行空间域上的重复任务,其周期特性主要存在于与位置相关的空间区间。因此,空间域上的学习控制方法研究受到越来越多国内外学者的关注[21-32]。文献[25]针对一类在有限空间区间内重复运行的二阶不确定运动系统,提出一种空间迭代学习控制方法,利用空间算子将系统不确定性转到空间域讨论,并通过半饱和学习律保证估计值的有界性。在此基础上,文献[26]将空间迭代学习控制方法拓展至一般形式的运动系统,并通过城市轨道交通进行了仿真验证。文献[27]针对数控机床系统轮廓误差不依赖于时间而依赖于空间的特点,设计空间迭代学习控制器,减少系统轮廓误差和提高数控加工精度。与空间迭代学习控制相比,空间重复学习控制（spatial repetitive learning control,SRLC）研究相对较少,且已有工作多基于空间内模原理[28-30]。文献[31]针对一类执行速度跟踪任务的旋转机械系统,提出一种基于李雅普诺夫方法的空间周期自适应控制方法。其中,控制器设计与误差收敛性分析均基于空间域进行。文献[32]针对永磁同步电机系统中的空间周期不确定,设计半饱和形式的空间参数自适应更新律加以估计和补偿。然而,文献[31,32]主要针对系统参数化不确定性设计空间重复学习律进行补偿,而非参数不确定运动系统的空间重复学习控制研究则鲜有报道。

基于以上讨论,本文针对一类执行空间重复任务的非参数不确定运动系统,提出一种基于李雅普诺夫方法的自适应空间重复学习控制策略,实现在空间域上系统速度信号对期望速度的高精度跟踪。首先,通过引入空间微分算子使被控系统转换为空间域形式。然后,将系统非参数不确定性划分为空间周期不确定和非周期不确定两部分,其中非周期性部分可通过使用Lipschitz 放缩将其转化为参数化形式,空间周期不确定则通过设计全饱和重复学习律进行估计和补偿。与已有的半饱和学习律相比,本文提出的全饱和重复学习律可保证估计值被限制在指定的界内。

1 问题的提出

本文考虑以下执行空间重复任务的非参数不确定运动系统[25]:

其中,x0是系统位置信号,x1为系统速度信号,α（x1） 是系统非参数不确定性部分,满足局部Lipschitz 连续条件,即|α（a）-α（b）|≤kα |a-b |,∀a,b∈R,其中,kα为一未知正常数。u（t） 表示控制输入,w（t） 表示有界外部扰动,满足|w（t）|≤ρ,ρ为一未知正常数。

由于系统式（1）在空间上执行重复任务,其周期特性主要存在于与位置相关的空间区间,因此,本文提出一种空间重复学习控制策略。为便于阐述所提控制方法,给出如下假设和定义。

假设1系统运动时始终朝一个方向做空间重复运动且速度恒大于0。

注1许多在空间域执行重复任务的实际运动系统正常运行时均满足假设1,例如火车、地铁、绕地球轨道旋转的卫星等。

定义1空间域上的系统状态定义为s,其表达式为

注2根据假设1 和定义1 可知,s随着时间t增加而单调递增,两者具有双射关系,即s=f（t） 存在反函数t=f-1（s）。因此,x1（t） 可以表示为关于s的函数x1（f-1（s））。同时,由初始条件x0（0）=0 以及式（3）,可得s=x0成立。下文中,将以s代替系统每次重复过程中的空间位置x0。

定义2系统每个空间周期运动的总路程定义为S,其表达式为

其中,T为系统运行过程中经过空间位置S所用的总时间。

由定义1 和定义2 可得,s∈[0,S]。由于本文考虑的系统周期性存在于空间位置s域,而非时间t域,因此,引入以下空间状态微分算子将传统时间域内描述的系统式（1）转换到空间位置s域上的表达形式。

定义3定义空间状态微分算子为

根据假设1 和定义1～3,利用空间微分算子式（4）可将系统式（1）等价转换为以下基于空间状态s的表达形式:

本文控制目标是针对执行空间重复任务的非参数不确定运动系统式（5）,设计空间自适应重复学习控制器u（s）,实现系统输出x1（s） 对空间周期性期望信号x1d（s） 的高精度跟踪。

2 控制器设计

在本节中,控制器设计和收敛性分析都在空间域进行。定义系统在空间域上的速度跟踪误差:

其中,x1d（s） 表示空间周期性期望信号。对x1d（s）在空间域求导可得:

由式（5）～（7）,对跟踪误差e在空间域求导可得:

其中,α=α（x1）,u=u（s）,w=w（s）。

定义Lyapunov 函数:

根据式（8）,对式（9）在空间域进行求导可得:

重复学习控制可以用来补偿周期性系统不确定性,然而,由于式（10）中的系统不确定性α没有表现出明显的周期特性,因而难以直接基于式（10）设计重复学习控制器。为此,本文引入空间周期为S的期望不确定性α（x1d） （简写为αd）,则式（10）可改写为如下形式:

与直接针对非参数不确定性α设计鲁棒补偿控制器相比,本文通过引入αd可以将待处理的非参数不确定性α划分为两部分,一部分是周期性非参数不确定αd,另一部分是非周期不确定性（α-αd）。其中,αd由于具有空间周期特性,可以通过设计空间重复学习律进行估计和精确补偿,而非周期不确定性α-αd则通过Lipschitz 条件放缩为参数化不确定性,并设计空间重复学习律估计其上界参数值,具体过程如下所述。

根据系统式（1）定义可知|α-αd |≤kα |e|,且利用杨氏不等式可知:

其中,ε为一正数。

因此,式（11）可进一步放缩为

根据式（13）,设计如下重复学习控制器u,其表达式为

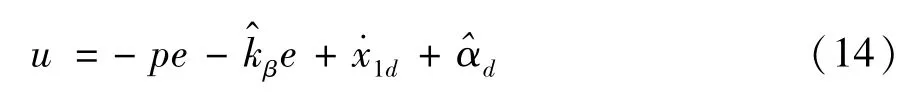
其中,p为一正常数,为kβ的估计值,为αd的估计值。

3 稳定性分析

本节将在空间域设计的重复学习律以及分析系统的收敛性。

分别设计如下形式的空间重复学习律更新和。

其中,μ1>0 为参数的学习增益,μ2>0 为参数学习增益。

将控制器式（14）代入式（13）可得:

定理1针对系统式（5）,给定空间周期期望速度信号x1d,设计空间重复学习控制器式（14）,以及重复学习律式（15）、（16）,则系统跟踪误差可收敛至原点附近的邻域内。

证明构造如式（18）所示的类Lyapunov 函数。

对U1和V1在空间域求导可得:

对式（18）在空间域求导可得:

将空间重复学习律式（15）代入式（26）可得:

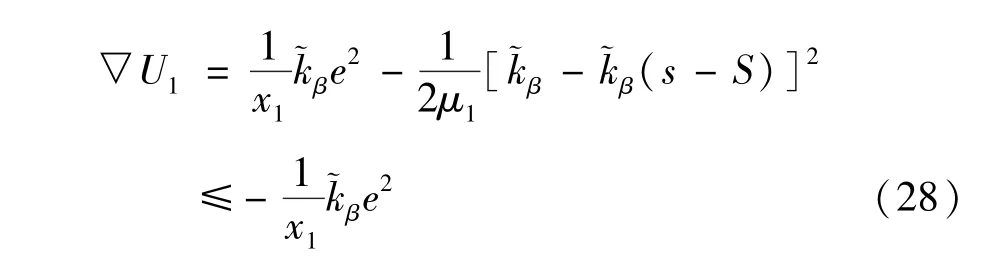
同理将空间重复学习律式（16）代入式（27）可得:

将式（17）、（28）和式（29）代入式（23）,可得:

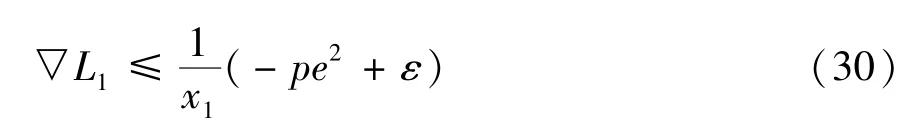
根据假设1,系统运动过程中x1恒大于0,由式（30）可得:

即|e|在区间s∈[S,∞） 有界,选择较小的参数ε和p,可保证跟踪误差e最终收敛到原点附近的邻域内,且该邻域随着ε值的减小或p值的增加而减小。证明成立。

注3根据式（31）可以分析出跟踪误差和参数ε和p的关系,但从式（13）、（14）中可知控制器增益为,较大的学习增益能够加快待学习参数的收敛速度,但同时会增大学习误差收敛的超调量,甚至引起振荡问题。因此,学习增益一般先选择较小的增益值,再根据学习误差的大小逐渐增大。

根据上述饱和函数定义,本文提出如下半饱和空间重复学习律:

其中,ϕ=ϕ（s）,该函数的主要作用是保证式（34）的连续性,其函数形式可选择为

由式（35）可以看出,ϕ函数在[0,S） 上单调递增,且满足ϕ（0）=0。

引理1对于任意给定变量a和b,若a处在sat（·）上下边界之内,则有如下不等式成立:

定理2针对系统式（5）,给定空间周期期望速度信号x1d,设计空间重复学习控制器式（14）,半饱和空间重复学习律式（33）、（34）,则系统跟踪误差可收敛至原点附近的邻域内,且可以保证估计值和的有界性。

证明构造如下类Lyapunov 函数

对式（37）在空间域求导可得:

▽W如式（17）所示,具体形式此处不再赘述,以下主要介绍如何处理▽U2和▽V2。根据kβ和αd的周期性可知kβ=kβ（s-S）,αd=αd（s-S）,因此▽U2和▽V2可改写为

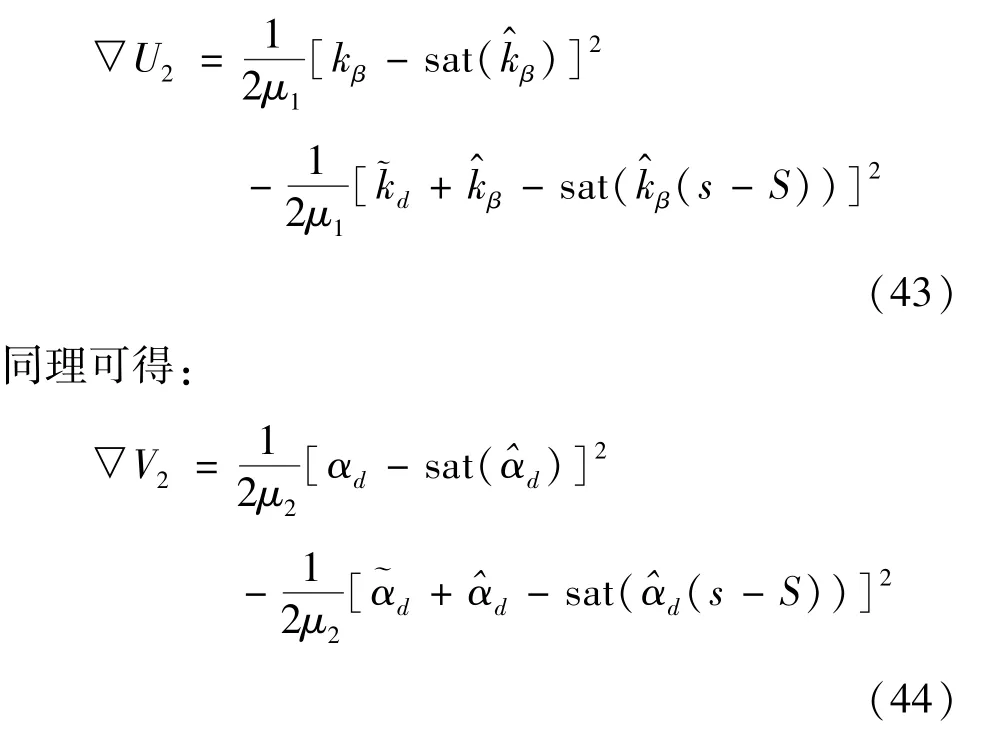
将式（33）代入式（43）可得:

同理,将式（34）代入式（44）可得:

根据引理1 可知:

将式（47）代入式（45）可得:

同理,将式（48）代入式（46）可得:

将式（17）、（49）和式（50）代入式（40）,则有:

继续分析跟踪误差|e|的收敛性,由于半饱和空间重复学习律式（33）和式（34）中通过区间分段定义和式（35）中ϕ的定义,无法直接在[0,∞）区间上分析|e |的收敛性,本文通过在[0,S） 和[S,∞）两个区间上分析|e|的收敛性,最终得出跟踪误差|e|在[0,∞） 区间上的收敛情况。

当s∈[0,S） 时,

由式（35）可知ϕ∈[0,1）,p为一正常数,由半饱和空间重复学习律式（33）、（34）可得的有界性。由式（32）可知的限幅值,因为,所以也是αd的限幅值。同理,为kβ的限幅值,只要设计控制器中参数,其中δ是一正常数,将式（53）代入式（52）可得:

当s∈[S,∞） 时,此时ϕ≡1。由式（51）可得:

此时可以得到和式（31）相同的结果,后续证明过程不再赘叙。综上可得,在保证估计值的有界前提下,系统跟踪误差可收敛至原点附近的邻域内,且该邻域随着ε值的减小或p值的增加而减小。证明成立。

相比空间重复学习律式（15）、（16）,半饱和空间重复学习律式（33）、（34）增加了对周期估计的限幅,但半饱和空间重复学习律中,未限幅项和的存在,使得难以被限制在指定的界内。因此,本文提出一种全饱和空间重复学习律,通过对分别进行限幅,确保被有效限制在指定的界内。全饱和空间重复学习律形式为

其中,ϕ=ϕ（s）,其表达式如式（33）所示。

引理2对于任意给定标量a和b,满足|a|≤,其中为b的限幅值,则有如下不等式成立。

定理3针对系统式（5）,给定空间周期期望速度信号x1d,设计空间重复学习控制器式（14）,以及全饱和空间重复学习律式（56）、（57）,则系统跟踪误差可收敛至原点附近的邻域内,且相比半饱和空间重复学习律式（33）、（34）只能保证估计值有界,全饱和空间重复学习律可以将估计值限制在指定的界内。

证明采用如式（37）所示的类Lyapunov 函数,在空间域对U2和V2求导:

根据饱和函数式（32）定义和引理2 可知η1≤0,η2≤0,故式（59）、（60）可改写为

将式（17）、（63）和式（64）代入式（40）,可得:

将全饱和重复学习律式（56）、（57）代入式（65）,可得:

后续证明过程与定理2 相似,故不再赘述。综上可得,在保证估计值有界的前提下,系统跟踪误差可收敛至原点附近的邻域内,且该邻域随着ε值的减小或p值的增加而减小,同时确保估计值在指定的界内。证明成立。

注4由本文控制目标可知系统输出期望信号x1d是一周期有界信号,从跟踪误差定义式（16）可知,当跟踪误差e收敛时,可以保证系统的速度信号x1有界。在控制器式（14）中,全局有界,本文设计的全饱和重复学习控制律能保证的有界性且能限制在指定的界内,跟踪误差e收敛时,控制器输出u有界。

注5文献[25]针对的是一类在有限空间区间内重复运行的运动系统,因而提出空间迭代学习控制方法,在迭代域上设计控制器和参数更新律。相比文献[25],本文针对的是一类在无穷空间区间内执行周期性重复任务的运动系统,提出空间重复学习控制方法,其控制器和参数更新律均是基于时间域进行设计。

4 仿真验证及分析

本节通过仿真实例验证所提空间重复学习控制方法（SRLC）的有效性。考虑空间域上的非参数不确定系统,其表达式为

为验证本文所提SRLC 方法的有效性,仿真中将本文方法与常用的比例积分（proportion integration,PI）控制方法进行对比。其中,PI 控制方法记为M1,其控制器表达形式为

其中,控制器参数设为Kp=2 和Ki=10。

本文方法记为M2,其中周期不确定性αd设为,构造空间重复学习控制器

其中,为保证对比公平性,M2 方法中的控制器增益p设置与M1 方法相同,p=2,kα=0.25,ε=1,ρ=1。空间全饱和重复学习律的表达式为

其中,学习增益分别设置为μ1=100 和μ2=300。ϕ=ϕ（s）,其表达式为

仿真结果如图1～图6 所示,其中图1 和图2 分别描述系统速度信号的跟踪效果与跟踪误差。由图1和图2 可以看出,M1 方法具有较快的跟踪速度,但稳态时仍存在明显的周期性跟踪误差。本文提出的M2 方法经过约2 个周期的重复学习,能够实现速度信号x1对期望信号x1d的精确跟踪。相比M1 方法,M2 方法具有更高的跟踪精度,且超调相对较小。同时,随着系统的周期运行,跟踪误差能够收敛至原点附近。两种方法的控制输入如图3 所示,从图中可以看出,两种方法的控制信号幅值相似,表明本文方法是相似控制输入幅值的情况下提高系统稳态跟踪性能。

图1 速度跟踪轨迹

图2 速度跟踪误差

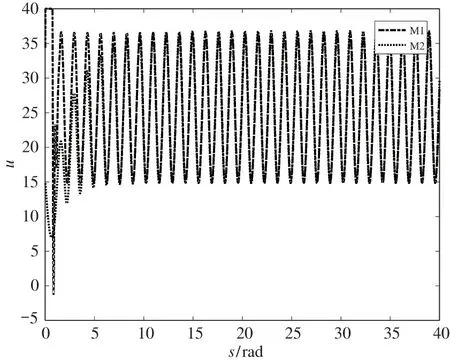
图3 控制输入

图4～图7 分别描述了M2 方法中空间非参数周期不确定αd和未知上界参数kβ的估计效果和估计误差。由图4～图7 可以看出,本文提出的空间全饱和重复学习律式（56）、（57）能够实现对系统空间未知上界参数的精确估计以及系统不确定性的有效补偿。此外,参数估计会逐渐趋于常值,这也表明本文提出的全饱和空间参数学习律能够保证参数估计值的有界性。

图4 周期非参数不确定性αd 及估计

图5 周期非参数不确定性估计误差～αd

图6 未知参数kβ 估计

图7 未知参数估计误差～kβ

5 结论

本文针对一类非参数不确定运动系统的速度跟踪问题,提出一种空间自适应重复学习控制方法,能够实现系统速度输出对期望速度的高精度跟踪。考虑系统运动的周期特性主要存在于与位置状态相关的空间区间,本文利用空间微分算子将系统从时间域转换到空间域,并在空间域上进行控制器设计与误差收敛性分析。通过引入空间周期为S的期望不确定性,将系统中的非参数不确定性划分为周期性非参数不确定和非周期不确定,并设计空间重复学习律加以估计和补偿。最后,通过严格的数学分析证明跟踪误差的收敛性,并给出仿真对比验证了本文方法的有效性。