门座起重机金属结构疲劳寿命估算方法
王 斌 何 然 文茂堂
深圳市质量安全检验检测研究院
1 引言
门座起重机(以下简称门机)是港口起重设备的重要组成部分,其安全使用问题始终是起重机厂家和使用户关心的首要问题之一。金属结构是起重机的受力骨架[1],也是起重机使用安全中最为关键的部分。研究统计表明,起重机的破坏和失效,大部分是由于金属结构的破坏所引起的[2]。老旧起重机由于已使用多年,有些已经接近或者超过其设计使用年限,起重机的金属结构内部难免会出现一定缺陷。这些缺陷和损伤由于隐蔽性较高,常规的年度检查以及维护保养中难以发现,这给起重机的安全使用埋下了巨大的隐患。组成起重机的重要金属结构件的应力状况能够反应金属结构在起重机工作过程中的受力情况,若结构件内部有缺陷,则其应力状况也会产生相应的变化。因此,为了保障起重机的安全使用,有必要对已使用多年的起重机主要金属结构件进行应力测试和分析。
目前,对起重机金属结构应力分析的研究,主要包含强度分析和疲劳分析两个方面。门机适用性较强,起吊载荷灵活多变,疲劳失效是其金属结构失效的主要形式[3]。通过运用应力测试方法,对一台港口现役单臂架门座起重机的主要金属结构件进行应力测试,并根据应力测试的结果,依据雨流计数法以及累计损伤理论,对该起重机主要金属结构件的剩余疲劳寿命进行了预测,为该起重机的安全运行提供了理论参考和依据,同时也为其他起重机械疲劳寿命预测提供了一定的技术参考。
2 主要金属构件应力数据测量
金属疲劳寿命的计算,依据计算时采用疲劳损伤模型的不同,拥有多种不同的方法,目前主要有名义应力法、局部应力应变法、断裂力学法[4]、应力严重系数法[5]、能量法[6]、损伤力学法等。考虑到门机所受载荷应力水平一般小于材料的屈服极限,处于较低水平,属于高周疲劳破坏,因此,用名义应力法进行疲劳寿命估算。
名义应力法,从材料的名义应力基本假定前提出发,结合测量部位应力集中的影响,对照待测材料的S-N曲线,采用损伤理论,用测得的应力值对材料的疲劳寿命进行估算。用名义应力法进行寿命估算时,首先应当对设备主要构件中易发生疲劳的危险部位进行应力测试,获取起重机工作时危险部位应力的变化情况。
2.1 设备概况和危险部位测点选取
本项目所检测门机型号为MQ40100,额定起重量为40 t,最大幅度为100 m,已投入使用12年。检查起重机金属结构件损伤的基本状况,并根据该起重机的结构特点,在臂架、圆筒、滑轮组支撑以及人字架等主要结构件中所受应力较大的截面处,选取16个测点作为应力测试点,具体测点布置见图1。

图1 应力测点布置图
2.2 测试工况和应力测试结果
现场测试时,考虑到待检测门机平时作业情况较为复杂,起吊载荷重量多变,且在接近额定载荷工况下使用频率较高,为了提高设备估算结果的安全系数,综合考虑设备的实际使用状况,采用额定载荷作为疲劳应力测试载荷,以设备在加载额定载荷,采用对应最大幅度进行装卸作业作为疲劳应力测试工况。
测试时,起重机具体的工作流程为:①吊具朝向海侧,载荷位于装料区,起升钢丝绳处于松弛状态时仪器调零,并开始记录测试数据;②起吊试验载荷并提升至设备常用装卸作业高度,根据装卸作业时的常用路径将臂架旋转180°;③旋转臂架回到初始装料区域,载荷落地,使起升钢丝绳完全松弛。以上工作流程视为该起重机装卸作业的1个工作循环。疲劳应力测试时,为了保证采集的应力数据能够更加真实准确地反映设备工作时的实际应力情况,需要对以上循环进行重复作业,以减少偶然随机因素的影响。本次测试中,对以上测试进行了10次重复作业和连续采样。
各测点在测试工况下的应力值情况统计见表1。
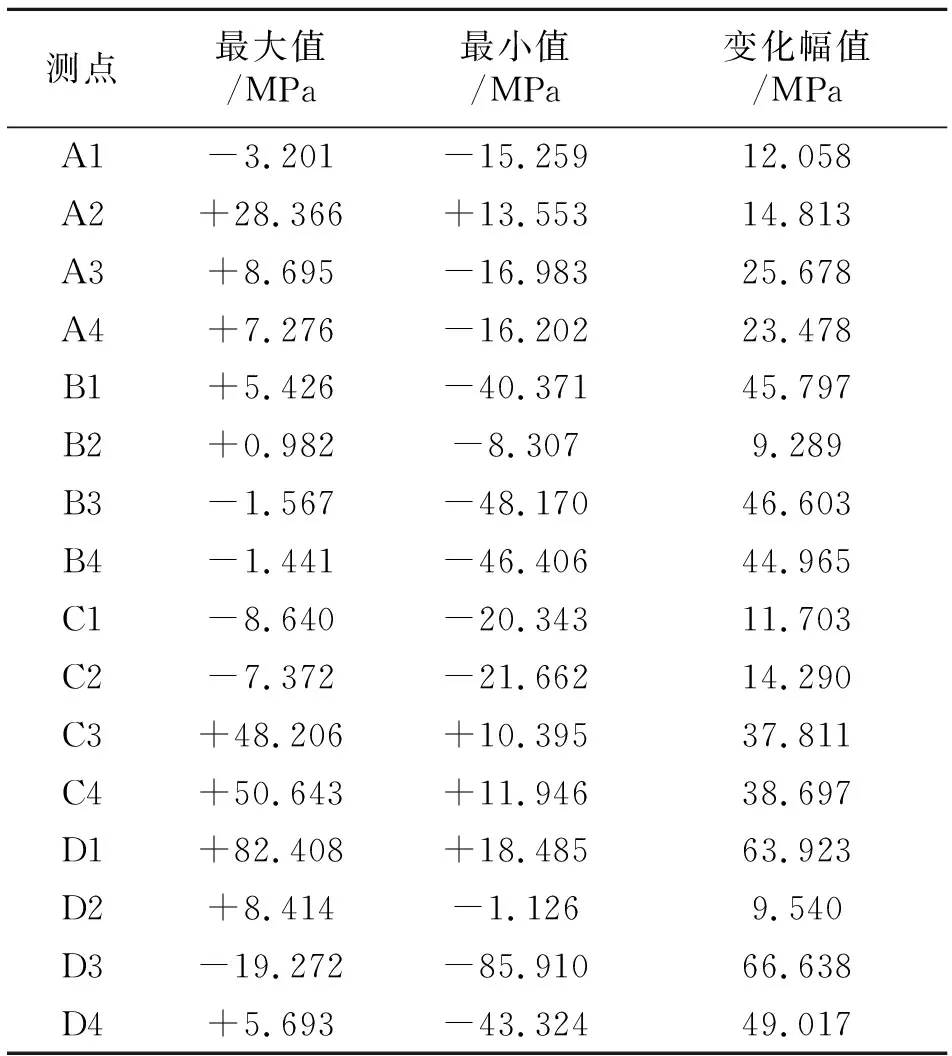
表1 各测点应力值情况统计
由表1可知,臂架根部测点B3、B4,以及圆筒处测点D1、D3,其应力最值和变化幅值较大。因此,进一步选取B3、B4、D1、D3作为疲劳危险点,进行疲劳寿命计算。
测点B3、B4以及测点D1、D3处的应力时间历程曲线分别见图2、图3。
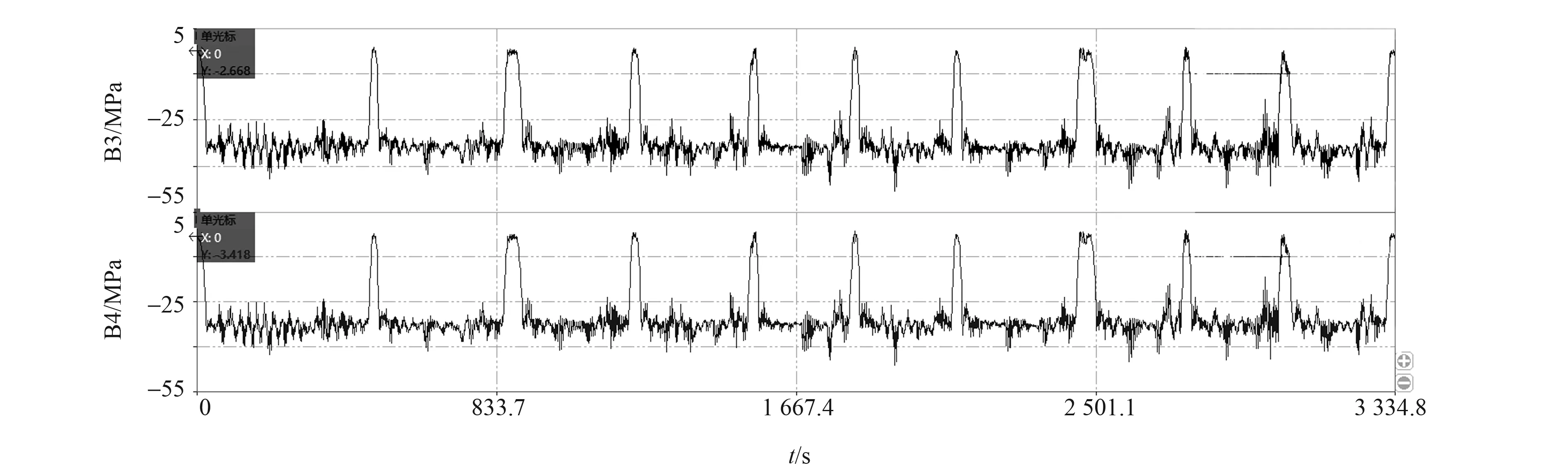
图2 测点B3、B4应力时间历程曲线

图3 测点D1、D3应力时间历程曲线
3 疲劳应力谱获取
通过对待测设备装卸作业时各测点的应力数据进行采集,获得了各选定测点在测试工况下的应力时间历程曲线数据。由于起重机工作过程中测点所受载荷作用的随机性,无法通过数学公式进行描述,必须借助统计方法对各测点的应力时间历程数据进行统计处理,将应力时间历程数据处理成疲劳应力谱,以便结合材料的S-N曲线进行进一步计算。
3.1 滤波处理
在应力数据测量过程中,受仪器以及外部环境的影响,所测得的应力时间历程数据通常会受到干扰信号的影响,从而产生一定的偏差,因此,需要对测量数据进行滤波处理,以减少干扰信号的影响。
3.2 峰谷点处理和雨流计数法统计
目前,国内外对于金属疲劳寿命的计算通常采用循环计数法中的雨流计数法[7-8]对应力数据进行统计处理。采用雨流计数法进行统计处理时,只对应力时间历程数据中的波峰和波谷点的幅值进行统计分析,因此需要对原始应力数据中的峰谷值进行筛选,去掉应力数据中的非峰谷点以及其他对金属疲劳寿命计算无影响的幅值小于最大幅值的峰谷点。
各危险测点应力测试数据,经过雨流计数法处理以后,便能获得能够反映测点在起重机工作过程中所受应力幅值、应力均值以及循环次数之间关系的疲劳应力载荷谱。
本次测试采用的DH5930便携式应变测试分析系统内含数据处理模块,数据后处理时可以直接调用相关模块,对数据进行滤波、峰谷以及雨流计数法统计。
4 剩余疲劳寿命估算
4.1 材料P-S-N曲线的确定
S-N曲线是以标准试样经过疲劳测试获得的表示材料外加应力幅和疲劳循环次数之间关系的曲线,不同材料的S-N曲线可以查阅疲劳设计手册获得。为了提高计算时的安全系数,标准的S-N曲线由于可靠度较低,难以满足寿命估算要求,因此通常采用可靠度更高的P-S-N曲线,将疲劳测试时的载荷抗力按随机变量来处理。
在工程实际中,通常采用双对数坐标形式,将材料的P-S-N曲线进行简化表达成直线形式,其表达式为:
lgN=C+mlgΔσ
(1)
式中,N为p%存活率下的疲劳寿命;Δσ为应力范围,MPa;C、m为不同材料及不同可靠度情况下的方程常数,根据所检测起重机主要焊接结构件的材料以及接头形式确定。本项目起重机的主要金属材料为Q235,在95%存活率下,C、m的值分别取为13.45与-3.371[9]。
4.2 平均应力的修正
反映材料疲劳性能的S-N曲线,通常是平均应力为零的基本S-N曲线。然而实际构件受载情况复杂,构件所受载荷平均应力大部分情况均值并不为零,因此,还应当对雨流计数法处理后获得的疲劳应力谱进行平均应力的修正,将有均值的应力谱先转换为均值为零的疲劳应力谱。
目前,常用的疲劳分析平均应力修正方法有Goodman法和Gerber法。Goodman法的表达方程为直线方程,简单易用,且估算关系较为保守,能够满足工程计算要求,Goodman法表达式为:
(2)
式中,σ′a为修正的应力幅值;σa为应力幅值;σm为平均应力;σb为材料的抗拉强度极限。
将经过雨流计数法处理后得到的应力幅值以及均值的分布图代入到上述公式中,即可获得修正后的应力幅值分布图。臂架处测点B3的应力幅值分布修正图见图4。
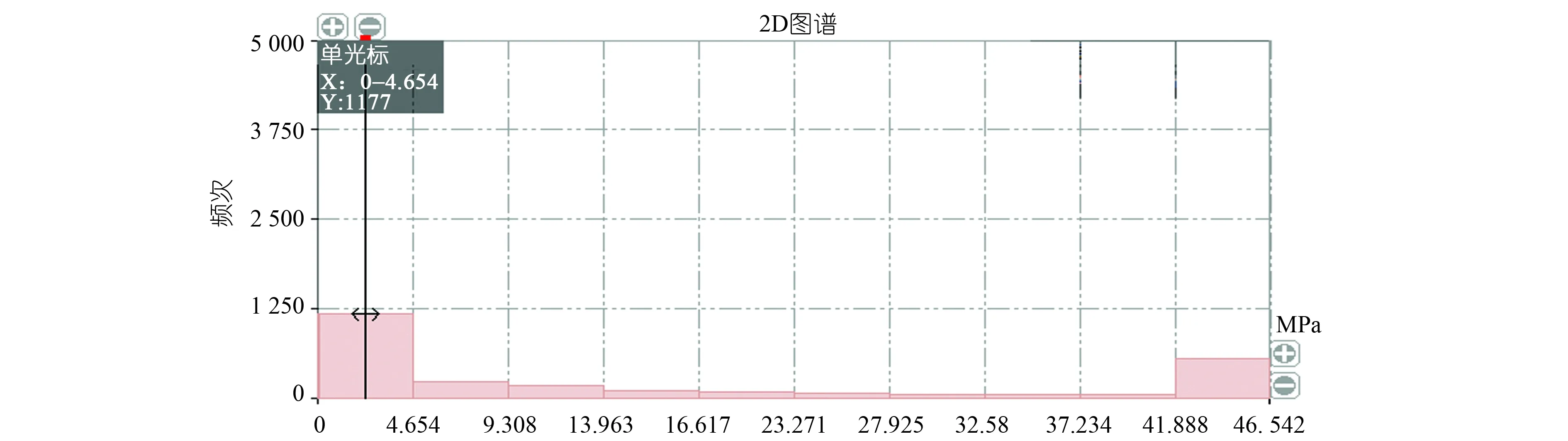
图4 臂架测点B3应力幅值分布修正图
4.3 剩余疲劳使用寿命估算
在金属结构疲劳寿命的研究过程中,许多学者根据疲劳损坏假设条件的不同得出了多种疲劳损伤方法。目前,Miner线性累积损伤方法由于模型简单,实用性和可靠性较高,已经获得了大量的应用。该方法用损伤度对工作循环中各应力水平所造成的损伤进行定量分析,并且假定各应力水平下的损伤度可以进行线性叠加[10]。
根据Miner线性累积损伤方法,采样应力循环下,不同应力水平所造成的损伤度D可以按照下式进行叠加计算:
(3)
式中,k为不同的应力水平级数,本项目将疲劳应力幅值分为10级进行计算,见图4;ni为采样时段内各级别应力水平的实际循环次数;Ni为在相应应力水平下达到疲劳时的总循环次数;a为安全常数,计算中取1,即假定材料的累计损伤度达到1时,则材料达到疲劳寿命上限。
将雨流计数处理以及平均应力修正后的应力幅值与相应循环次数的分布情况数据用P-S-N曲线进行对应疲劳循环次数计算,即可获得各应力水平作用下达到疲劳时的循环作用次数,最后用Miner线性损伤方法将各应力水平的损伤度进行叠加,便能获得各测点在采样时间内的总体损伤度D′。
假设采样时间长度为t,起重机服役过程中始终按照采样工况进行装卸作业,则可以由采样时间长度下各测点的损伤度推导计算该起重机达到疲劳时所需的总时长,即为其疲劳寿命。疲劳寿命H理论计算公式可以表达为:
(4)
式中,总损伤度D取1。
结合设备的已使用年限,即可得到设备的剩余疲劳使用寿命T为:
T=H-H′
(5)
式中,H′为设备的已使用年数。
根据使用方提供的设备使用情况记录,所检测起重机已使用年数H′为12年,设备1天工作约8 h,1年工作约250 d,则B3、B4、D1、D3这4个危险测点剩余疲劳寿命计算结果见表2。

表2 危险测点剩余疲劳寿命情况统计
由表2可知,该起重机圆筒处疲劳寿命最短,其中D3测点的剩余疲劳寿命为6.5年。
5 结语
对1台港口门机进行了应力测试,根据应力测试的结果,针对该起重机的结构形式进一步选定4个应力测量值较大的点作为疲劳危险点进行疲劳寿命分析。由应力测试所得的疲劳危险点处应力时间历程数据,通过雨流计数、应力修正等方法进行数据处理,结合起重机金属材料的P-S-N曲线以及Miner线性累计损伤方法对危险测点的剩余疲劳寿命进行了估算。计算结果显示该起重机圆筒处疲劳寿命最短,剩余疲劳寿命为6.5年。
起重机疲劳寿命计算的结果让用户对设备有了进一步的了解,为今后对设备的科学管理和维护提供了参考和依据,同时对类似结构起重机的疲劳寿命预测工作也具有一定的指导意义。

