挤压速度对SAC3005锡焊料挤压过程和应力应变影响的有限元分析*

梁华鑫，陈东东，白海龙，赵玲彦，严继康

（1.云南锡业集团（控股）有限责任公司研发中心，云南 昆明 650032；2.昆明理工大学材料科学与工程学院，云南 昆明 650093；3.西南石油大学工程学院，四川 南充 637001）

焊锡丝是手工烙铁焊接、SMT焊后补修的重要焊接材料[1]，随着精密焊接领域的发展，电子元器件尺寸不断减小，所需要的焊锡丝要求线径更细、质量更高。目前焊锡丝传统生产工艺主要是挤压技术，包含铸锭、挤压、轧辊、拉丝等生产工艺[2]，但产品存在表面质量差、成分偏析大、生产效率低等问题。采用分流挤压技术对锡焊料挤压时，金属流动较复杂，其变形行为研究也较为困难。为了满足对挤压产品高质量、高成品率等方面的要求，采用实验与数值模拟相结合的方法研究分流挤压变形过程受到越来越多的重视[3]，在预测产品的工艺缺陷和提高产品质量的同时，可有效减少实际调试生产所需的人力、物力及时间成本[4]。

Kargin V R等[5]通过Deform有限元软件对热变形过程中塑性变形区域不同截面和成品中应力和应变的分布进行了模拟分析，确定了挤压比值对直径500 mm至250 mm变形过程中应力-应变的影响。Zhou J等[6]利用DEFORM 3D软件对铝合金坯料的挤压过程进行研究，通过对不同形状的坯料进行挤压，成功预测了完整的挤出压力/柱塞位移图，并对坯料内部的挤压速度、有效应变和温度的变化进行了分析，以上研究显示了应用模拟方法的优势。另外，在焊锡丝的挤压制备过程中，合金的组织对后续的加工性能有很大的影响，数值模拟为工艺的改进提供了更加便捷的手段。张君[7]等采用理论分析和有限元模拟结合的方法，研究了3种不同挤压工艺中挤压力、挤压筒受力与挤压行程的曲线对比关系，并建立了相应的计算公式，通过实验证明铝型材沿长度方向的均匀性有所提高，型材表面的粗晶环得到减少甚至消除，得到了高性能精密工业铝型材。Asfandiyarov R N[8]等采用径向锻造和ECAP-Conform法相结合方法制备合金丝，通过计算机仿真研究了塑形加工中的应力-应变状态和热力学条件，研究发现合金的延展性提高了50%。

为了进一步提高电子焊接用焊锡丝的产品质量、优化工艺参数，本文采用DEFORM-3D有限元软件模拟锡合金挤压过程，对关键位置的应力、应变进行分析，为实际生产提供有效参考[9-13]。

1 挤压工艺有限元模型的建立

焊锡丝在拉拔过程中需要的合金杆主要由挤压工艺制备而来的，在挤压过程中，焊料合金在挤压模处开始分流，从分流孔中进入，在压力的作用下，在焊合腔中实现焊合成杆，同时完成助焊剂的注入。本研究针对焊料合金的变形过程进行分析，变形过程不再关注助焊剂的注入情况。以直径80 mm的圆柱形挤压锭制备直径12 mm的空心锡杆，保证空心锡杆挤压过程中空心管路不变形，不闭合，以便保证助焊剂连续注入空心形成有芯焊丝，为后续的辊轧、拉拔和拉丝工序提供无断芯的锡合金杆。

本文根据实际挤压模具的结构进行相应的几何模型建立和有限元模型建立。采用SolidWork进行三维建模，模具主要由三个部分构成：挤压模、模芯和下模，如图1所示。

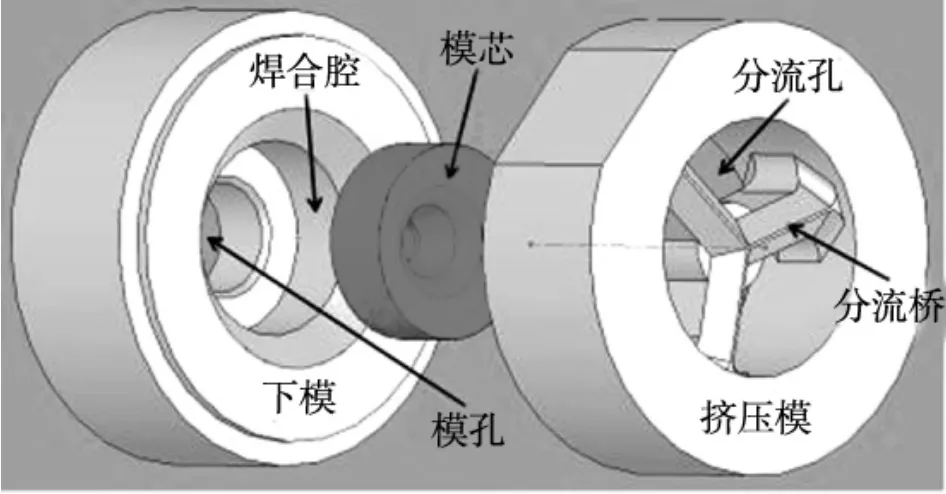
图1 挤压模具三维模型Fig.1 3D model of extrusion mould

有限元模型建立时，将分流上模、模芯和挤压下模与挤压筒相配合成为挤压模具，在挤压筒体内设置坯料，圆柱形推块作为运动部件给坯料施加挤压力，示意图如图2所示。设置坯料温度为80℃，挤压速度分别为10 mm/s、20 mm/s、30 mm/s；坯料属性选择根据焊锡产品开发的需要，选定为Sn-Ag3.0-Cu0.5，定义为弹塑性材料；模具、挤压筒、挤压推块选用H13钢，其具有强韧的力学性能，在挤压过程中不考虑凸模和挤压模的受力情况，定义为刚性材料[14]。结合仿真模拟的实际情况，采用四面体单元来划分网格，在挤压过程中发生网格畸变时可以更加精确地实现网格重划分，考量了计算的精度和计算规模将挤压坯料网格设置划分为100 000个单元。在实际的常规挤压过程中，坯料与挤压模具以及挤压筒之间存在摩擦升温，坯料、模具以及环境之间存在温度差就会产生热量的传递，为了简化分析计算的过程，单纯的考虑坯料温度改变对金属挤压变形的影响，即对数值模拟做出了模具绝热的假设。

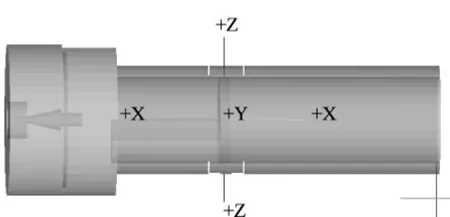
图2 挤压示意图Fig.2 Schematic diagram of extrusion

2 结果与讨论

2.1 焊合过程分析

挤压制杆过程中，合金经过分流桥之后完成焊合，焊合质量对产品有较大的影响，现分析坯料温度为80℃，挤压速度分别为10 mm/s、20 mm/s、30 mm/s时，挤压速度对于焊合过程中型材截面形状的影响。如图3所示，当挤压进行到1.22 s时，挤压速度为30 mm/s的分流坯料已经开始接触，焊合即将完成，而10 mm/s、20 mm/s的模拟坯料分流才刚刚开始；如图4所示，当挤压进行到约1.97 s时，20 mm/s条件下的挤压模拟焊合完成，型材基本成型，而10 mm/s条件下的模拟在2.01 s时仍然处于分流的阶段，在30 mm/s条件下1.31 s时型材就已经完全成型，并且截面形状趋于理想。对比发现：在挤压的焊合阶段，挤压速度对于截面形状的影响是不明显的，但是挤压速度越快，型材挤压完成所需要的时间就越短，有利于提高生产效率，结合设备的负荷极限，在以上三个挤压速度下30 mm/s为最优条件。

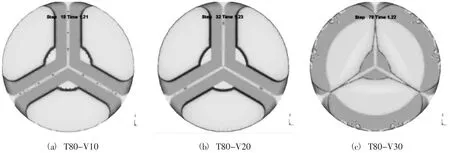
图3 t=1.22s时三个挤压速度条件下的的焊合情况Fig.3 Seaming situation with three extrusion speed conditions when t=1.22 s

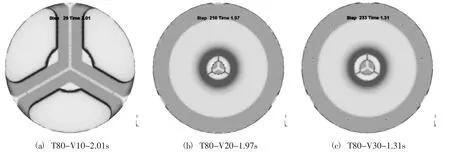
图4 不同挤压速度条件下的的焊合情况Fig.4 Seaming situation with different extrusion speed conditions

2.2 有效应变分析

在挤压过程坯料变形分析的基础上，对变形过程中坯料不同位置的有效应变和有效应力进行分析。图5是坯料不同位置的取点示意图，本文分别对坯料与分流桥接触的不同点P1、P7、P8、P9进行应变和应力分析。

图5 取点示意图Fig.5 Schematic diagram of sampling point

图6是在相同的坯料温度下，挤压速度分别为10 mm/s、20 mm/s、30 mm/s时的有效应变的变化曲线。其中图6（a） 是点P1的有效应变曲线，在1.5 s以前，有效应变趋近于零且随着时间没有明显增长变化；约在1.5 s到3.5 s间，随着挤压的进行有效应变的增长趋于明显；3.5 s至4 s间，有效应变骤增，在约0.5 s的时间内，有效应变数值从几十增长到了几百，三个挤压条件下的有效应变值开始趋于一致。在1.5 s至4 s有效应数值明显增长的区间，10 mm/s条件下的坯料有效应变数值增长速率最大，有效应变值最大，30 mm/s条件下的坯料增长速率最慢，有效应变值最小，但三个挤压速度下的坯料的有效应变值差距很小。图6（b） 是点P7的有效应变曲线，图6（c） 是点P8的有效应变曲线，图6（d）是点P9的有效应变曲线，进行对比发现，在前4 s阶段，三个点在不同挤压速度下有效应变的变化与P1点变化部分相似。不同的是，在1.5 s至4 s有效应数值有明显增长的区间，三个点在不同挤压速度条件下的有效应变值差距更小，增长速率几乎一致。因此，由图6可知：在相同的坯料温度条件下，挤压速度变化对于坯料的有效应变影响较小。

图6 不同挤压速度下的坯料的有效应变Fig.6 The effective stress-strain of blank with the different extrusion speed

2.3 有效应力分析

经过挤压过程坯料各个位置应变的分析，不同的挤压速度对应变影响不大，现分析坯料温度为80℃时，比较挤压速度10 mm/s、20 mm/s、30 mm/s对有效应力的影响。图7为坯料温度为80℃时，不同挤压速度10 mm/s、2 mm/s、30 mm/s条件对有效应力影响曲线。图7（a）为点P1的有效应力曲线，从0 s开始，挤压速度为20 mm/s、30 mm/s的坯料有效应力开始增加，0.15 s时有效应力达到最大值，挤压速度为10 mm/s条件下的坯料有效应力变化有所延迟，约0.1 s时开始增加至0.15 s与其余两个条件下的坯料几乎同时达到最大值，且30 mm/s条件下的有效应力值最大，10 mm/s条件下的最小，而后应力值呈现锯齿状上下浮动，自1.0 s以后，数值锯齿状浮动现象更为密集和明显。图7（b） 是点P7的有效应力曲线，在0.15 s之前阶段，应力变化和P1点变化一致，但之后三个条件下的有效应力值呈抛物线的形状有一定程度的下降和回升，回升至0.65 s附近出现几乎达到有效应力最大值的一个值峰，30 mm/s条件值峰出现的时间为0.6 s，20 mm/s条件值峰出现的时间为0.65 s，10 mm/s条件值峰出现的时间为0.7 s，值峰后至1 s的时间段内应力值有较为明显的下降趋势，1 s后有效应力值呈锯齿状出现明显的上升状态，直至与最大有效应力值相接近。图7（c） 是点P8的有效应力曲线，可以看出与点P7的有效应力曲线变化几乎一致。图7（d）是P9点的有效应力曲线，其总体变化规律和P1点接近，但在1 s之后的应力增加的更加平缓，相比于其他各个位置，此处的应力值达到最大。因此，由图7可知，在相同的坯料温度条件下，随着挤压速度的增加有效应力值有所上升，但影响值不大。

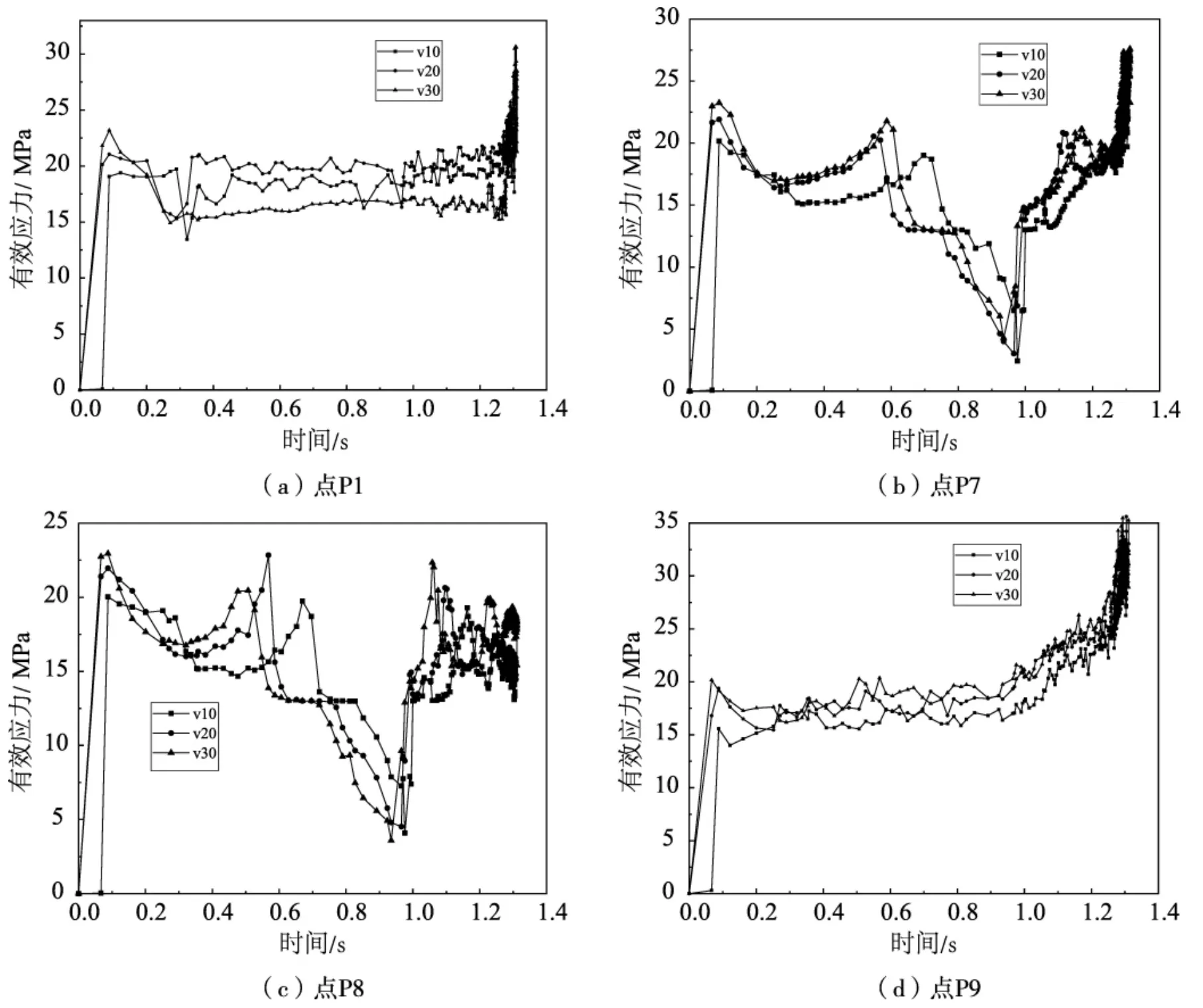
图7 不同挤压速度下的坯料的有效应力Fig.7 The effective stress of blank with the different extrusion speed

2.4 应力-应变分析

以上分别对各点的应变、应力进行了单独分析，为了比较各点的应力随着应变的变化，现对挤压速度10 mm/s、20 mm/s、30 mm/s时的应力和应变进行综合分析。图8为坯料温度80℃时，不同挤压速度条件下的挤压过程中，坯料的应力-应变比较曲线。图8（a） 是P1点的应力-应变曲线，图8（b） 是P7点的应力-应变曲线，图8（c） 是P8点的应力-应变曲线，图8（d） 是P9点的应力-应变曲线，比较分析发现4个点的应力-应变曲线趋势相似：自有效应变值为0 mm/mm开始，有效应力值开始增加，并且在很小的应变区间内迅速由0增长到20 MPa左右，自有效应变值15 mm/mm以后，有效应力曲线呈锯齿状叠加在近似抛物线上。应力-应变曲线从图中可以分为两个变形阶段：应力-应变线性变化的弹性变形阶段，平台区数据呈现锯齿状波动的不均匀塑性变形阶段。比较4个点在不同挤压速度下的塑性平台区应力，30 mm/s条件下的平台区应力值最大，10 mm/s条件下的最小。塑性平台区的应力值越大，材料的抗脆断裂强度越低，即材料的脆性越大，塑性越小。因此，由图8可知，在相同的坯料温度条件下，随着挤压速度的增加，坯料的塑性平台区应力值即屈服极限值有所增大，坯料塑性越差，加工性能越差。

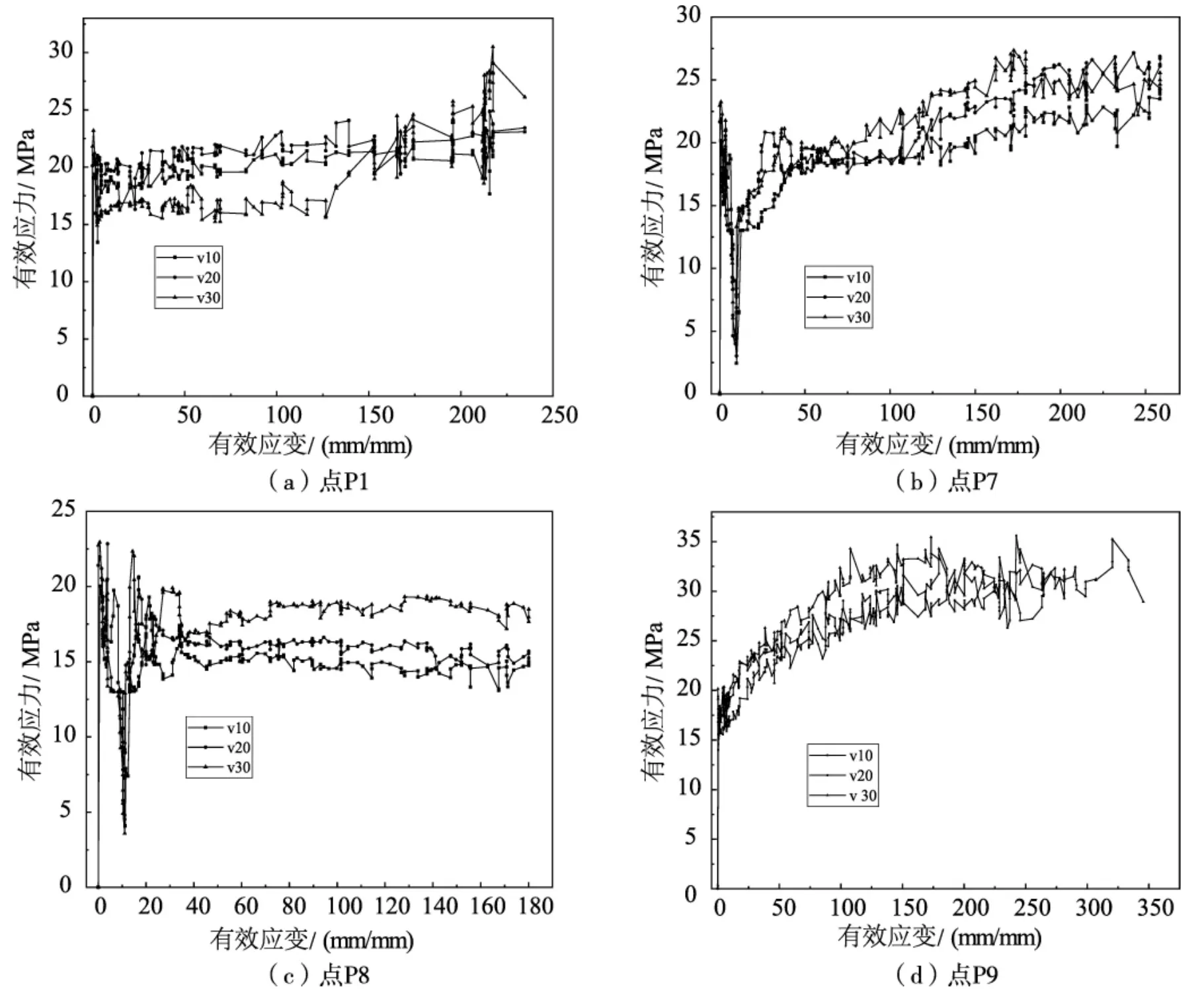
图8 不同挤压速度下的坯料的应力-应变Fig.8 The effective stress-strain of blank with the different extrusion speed

3 结语

基于DEFORM软件，对焊锡丝制备用焊锡杆的挤压成型过程进行了模拟，分析了在不同的挤压速度下合金的应力应变等变化。

1）在挤压的模拟中发现，挤压速度对挤压分流的焊合影响不大；随着挤压速度的增加，坯料的应变在3.5 s至4 s之间剧增；

2） 坯料的有效应力在0.15 s时达到最大值，但10 mm/s条件下略有延迟；

3） 随着挤压速度的增加，坯料的应力-应变值增加，提高了挤压杆脆性断裂的风险，同时为了兼顾加工效率，20 mm/s为最佳挤压速度。