边缘计算中基于马尔可夫决策过程的数据分流时间优化

杨桂松，候 玲，何杏宇

1(上海理工大学 光电信息与计算机工程学院，上海 200093) 2(上海理工大学 出版印刷与艺术设计学院，上海 200093)

1 引 言

近年来，随着物联网的发展，据HIS markit预测，到2025年，物联网设备将增长约750亿台[1].这些用于感知和传输数据终端设备数量的急速增长会导致在网络中传输数据的急速增长，因而会增大网络负载及数据传输时延.此外，随着人工智能的不断发展，深度学习需要GPU并行计算，耗费了大量的计算资源，产生大量的数据.因此，如何低时延高效率的处理数据成为当前研究的热点.

为缓解由于数据增长带来的网络负载过大以及处理时间长的问题，最直接的方法是升级网络以提升网络容量和网络传输速率[2].但是由于升级网络设备存在部署和成本问题，许多研究者开始研究通过数据分流来解决数据传输时延大的问题.随着云计算的出现，终端设备能将数据上传到云端处理，以满足数据对截止时间敏感的需求[3].但由于云端与终端设备之间距离较远，这会增加数据的传输时间，降低网络服务质量.近年来，边缘计算作为一种新型的网络结构被提出，用来解决云端与终端设备距离远的问题.边缘计算是指将原有云计算中心的部分或全部任务迁移到数据源的附近执行[4].

在边缘计算中进行数据分流时，分流节点是指被终端设备选择用于数据分流的边缘设备，如何选择最优的分流节点是低时延高效率处理数据的关键.在文献[5]中，作者在蜂窝网络和无线局域网的环境中，提出基于深度强化学习技术的最优分流策略，结合神经网络和Q-learning算法选择分流节点以达到同时分流多种数据的效果，但由于传统宏蜂窝基站会存在弱信号质量问题[6].在文献[7]借助小型蜂窝基站辅助的方法来提供高吞吐率和高可靠性的网络连接，联合优化吞吐率和传输功率，并采用垂直分解的方法实现大量智能设备的数据分流，但这项工作在设计分流方案时没有考虑系统的不确定性.文献[8]中，作者基于节点接触形成的通信机会传输数据，借助机会传输与主动部署感知网络相结合的方式来满足数据交换和数据收集的需求，但是它未关注节点之间的接触概率.文献[9]中，作者基于节点的接触概率预测，通过区间数的不确定性理论和区间数比较方法，提出一种预测辅助的数据传输机制，以提高数据的传输成功率，但是这种预测方法依赖对历史数据的统计分析，忽略了终端设备与环境之间的交互.文献[10]中，作者基于马尔科夫(MDP)决策过程，提出多路径冗余传输调度算法，实现对关键数据的实时性传输，提高数据传输可靠性.该算法根据网络当前状态对数据块以及传输路径数目进行建模，来选择当前状态下最优的分流节点，但是未考虑数据量的大小对数据传输带来的影响.在文献[11]中，作者研究多个应用程序产生的多流数据分流问题，通过考虑多个文件剩余数据量大小，提出一种低时间复杂度的启发式分流算法，满足不同应用程序的数据对不同截止时间的需求.但是这种分流策略没有考虑终端设备的移动性，而终端设备的位置变化会影响分流的效果.

针对上述工作存在的不足，本文在研究边缘计算中数据分流的问题时，提出一种基于马尔可夫决策过程的最优分流节点选择策略来保证数据传输的同时达到优化分流时间的效果.首先，本文通过在边缘层中部署微型蜂窝基站和WiFi AP作为分流节点，提出一个支持蜂窝和WiFi通信的网络模型；然后，联合考虑终端设备的位置以及上传数据量的大小构建马尔可夫决策过程模型；最后通过值迭代算法求解马尔可夫决策过程模型，得到最优分流节点选择策略.通过与两个对比实验比较，实验结果显示：本文提出的最优分流节点选择策略在优化分流时间的效果上有明显提升.

2 系统模型

2.1 网络模型

边缘计算中用于流量分流的网络模型如图1所示.其中，为方便描述，模型中使用网格的方式来描述终端设备和边缘设备的位置.边缘计算的网络模型层次划分为：“终端层-边缘层-云层”.终端层由需要上传数据的终端设备组成.终端设备具有移动性，它在移动过程中采用两维无记忆移动模型[12]，且在移动时能实时上传自己的位置；边缘层是由微蜂窝基站和WiFi AP两种分流节点组成.在边缘层中，边缘设备部署位置随机且固定，每一个边缘设备有唯一的编号.云层中部署了能为终端设备提供全覆盖的网络通信保证的宏蜂窝基站，当终端设备不在任何边缘设备的通信范围内时，终端设备将数据分流到云层.由于本文云层只是作为补充手段，重点考虑在边缘层中选择分流节点分流数据，故在图1中没有显示云层.

图1 网络模型Fig.1 Network model

在终端层，终端设备在移动的过程中产生需要上传的数据.这些数据之间的拓扑结构可以是线性、树状或网格等形式，考虑到分流数据可顺序分流这一事实[13]，因此，在本文中，终端设备以线性的方式顺序分流数据.边缘层中共部署由微型蜂窝基站和WiFi AP组成的M个边缘设备.其中，这两种边缘分别支持蜂窝通信和WiFi通信技术，对于支持不同的通信技术的边缘设备，其无线通信半径与网络传输速率不同.

2.2 马尔科夫决策过程模型

在如图1所示的网络模型中，考虑到终端设备的位置和上传数据量的大小都具有不确定性，而马尔科夫决策过程是一种有效的数学模型，它能用来在不确定的动态系统中做出最优的序列决策.因此，本文将最优分流节点选择问题建模成马尔科夫决策过程模型.

马尔科夫决策过程模型由5个元素组成：决策时期、状态空间、动作集、转换概率、回报函数.

1)决策时期T:决策时期表示终端设备选择分流节点的时间，每一个决策时期的时长为Te.

T={1,2,…,t,…,k}

(1)

其中，k表示终端设备需要执行数据分流的次数.

2)状态空间S：状态空间由终端设备选择的分流节点编号、上传数据量大小及终端设备当前所处位置的网格编号组成，定义如下:

S=N×F×L

(2)

其中，N=[N1,N2,…,Ni,…,NM]是一个M维数组,表示可用于分流数据的M个分流节点.Ni∈{0,1},i=1，2，…，M.Ni=1表示终端设备在分流节点i的通信范围内，Ni=0表示终端设备不在分流节点i的通信范围内.F=[F1,F2,…,Fj,…,Fk]是一个k维数组，表示终端设备在每个决策时期需要分流的数据量大小.L=[L1,L2,…,Ll,…,LG]是一个G维数组,表示终端设备所有可能移动的G个网格的编号.

3)动作集A：在一个决策时期t内，终端设备根据当前状态，从动作集A中选择一个动作a来分流数据.行为集定义如下:

(3)

4)转换概率P：给定当前状态s=[Ni,Fj,Ll]以及选定的动作a,转换到下一个状态s′=[N′i,F′j,L′l]的概率，定义如下:

(4)

其中，P(L′l|Ll)表示终端设备从格子Ll移动到格子L′l的概率.

(5)

其中，μ是位置稳定概率，0≤μ≤1，它表示终端设备在两个连续决策时期定位在同一个网格内的概率.相应地，终端设备会以概率ρ随机移动到相邻格子.ρ的具体计算公式如下:

ρ=(1-μ)/g

(6)

其中，g表示与当前格子Ll相邻的格子L′l的数目.

对于终端设备需分流的数据量大小的变化概率，定义如下:

(7)

P[F′j|Fj]表示终端设备上传数据量从Fj转换到F′j的概率.其中，ri表示终端设备选中的分流节点的数据传输率.

5)回报函数f:终端设备在当前状态s选择一个动作a后，将得到一个与分流时间相关的回报函数f(s,a).

(8)

其中，TWiFi和TCell分别表示选择WiFi AP和微型蜂窝基站分流数据得到的分流时间.对于上传数据的分流时间计算公式如下:

当选择的分流节点是WiFi AP:

(9)

当选择的分流节点是微型蜂窝基站:

(10)

其中，Fj表示上传数据量大小.微型蜂窝基站的通信半径是Rci，数据传输率是rci；WiFi AP的通信半径是Rwi，数据传输率是rwi.d表示终端设备和分流节点之间的距离.

3 基于MDP的最优分流节点选择策略

这一节重点将介绍通过值迭代算法求解MDP模型得到最优分流节点选择策略的过程.基于MDP的最优分流节点选择策略的目的是在k次上传数据分流的过程中，从M个分流节点中选择最优的分流节点分流数据以达到优化分流时间的效果.

在求解的过程中，值函数vπ(s)用来表示当初始状态为s，采用分流节点选择策略π时得到的回报值.该回报值由当前决策时期的立即回报以及接下来的每个决策时期产生的未来回报之和表示.

(11)

其中，E[·]是期望函数，它表示终端设备的初始状态是s, 分流节点选择策略是π时的期望值；ft(s,a)表示在决策时期t时，终端设备得到的立即回报；λ是折扣因子，用来衡量未来回报的重要程度，λ∈(0,1].λ越接近1，未来回报的权重越大[14].

特别地，由于基于MDP的最优分流节点选择策略的目的是优化分流时间，所以，v(s)用来表示在初始状态s下，从所有的分流节点选择策略∏中得出的最优分流时间.

(12)

上式用贝尔曼方程[15]表达为:

(13)

由于值迭代算法(VIA)的理论简单、易于编码，因此，在本文中，运用值迭代算法求解MDP模型得到基于MDP的最优分流节点选择策略.

(14)

一般来说，值迭代算法的时间复杂度为O(|A||S|2)[16].其中，|S|和|A|分别表示状态空间和动作集的大小.值迭代算法在求解MDP模型时，首先输入决策时期、状态空间、动作集、转换概率、回报函数.初始化阶段，将所有状态、动作的回报值初始化为零，形成一个|S|行|A|列的全零矩阵.并将用于标记迭代次数的x初始化为0，将阈值ε初始化为一个极小的正数.迭代阶段，在每一个决策时期，根据终端设备当前的状态以及可采取的动作，通过MDP模型中的转换概率，计算在当前状态下，选择每一种动作获得的回报值.再在当前状态下，从选择不同动作得到的不同回报值中选出最小的回报值，用于下一阶段的判断及下一次的迭代.判断阶段，该阶段通过计算上一阶段的回报值vx+1(s)与上一次迭代的回报值vx(s)的差值，将差值与阈值进行比较.若两次的差值小于阈值，则返回最优分流时间v(s)及最优分流节点选择策略π*(s)；否则，则用上一阶段的回报值进行下一次迭代.最终，当值迭代算法终止时，算法1输出基于MDP的最优分流节点选择策略.对于给定的状态，终端设备能根据该策略选择最优的动作分流数据达到优化分流时间的效果.

值迭代算法的伪代码介绍如下：

算法1.基于MDP的最优分流节点选择策略

输入：决策时期、状态空间、动作集、转换概率、回报函数

输出：最优分流节点选择策略

a)初始化：∀s∈S，∀a∈A，vx(s)=0，x=0，ε>0

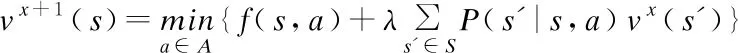
c)判断:

如果vx+1(s)-vx(s)<ε，则返回d);

如果vx+1(s)-vx(s)>ε，则x=x+1,返回b)

d)返回:v(s)，π*(s)//根据公式(13)、公式(14)

4 实验以及结果分析

4.1 实验环境

为评估基于MDP的分流节点选择策略在优化分流时间上的性能，使用仿真软件在超级计算中心曙光 TC4600E 百亿次超级计算系统上进行100次实验.实验环境如表1所示.

表1 实验环境Table 1 Lab environment

4.2 实验参数

实验参数如表2所示.

4.3 实验分析

本文提出基于MDP的分流节点选择策略(MDP)，选择最优分流节点来优化分流时间.为评估本文所提策略在优化分流时间上的性能，本文采用两个对比实验对实验结果进行比较分析.

基准算法为随机分流节点选择策略(Random)[17]和优先WiFi分流节点选择策略(OTSO)[18].其中，Random采用随机的思想，从能与终端设备进行通信的分流节点中随机选择分流节点分流数据.OTSO在选择分流节点时，终端用户一旦能与WiFi AP通信，便选择WiFi AP节点分流数据.

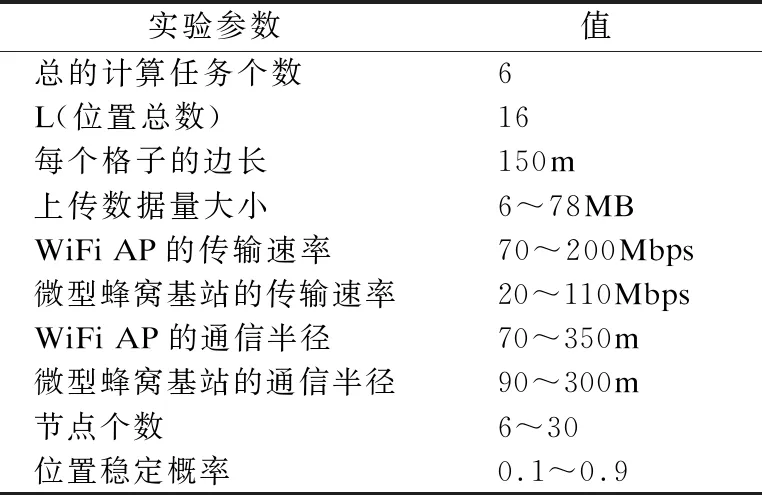
表2 实验参数Table 2 Lab parameters

本文所提算法为基于MDP的分流节点选择策略(MDP)，终端设备根据该策略选择分流节点分流数据.具体来说，算法首先通过2.1节中的网络模型确定状态空间和动作集.根据终端设备选择的动作，考虑终端设备位置和需要分流的数据量大小的变化，根据公式(4)计算不同状态之间的转换概率，得到转换概率矩阵.通过转换概率矩阵和回报函数，根据公式(11)求出每一种状态下的回报值，得到回报值表.最终通过迭代回报值表中的回报值，选择每一种策略下最小的回报值，得到最优分流节点选择策略.在数据分流完成之前，终端设备在分流数据时，在给定状态下，根据最优分流节点选择策略，选择最优的分流节点分流数据.

根据2.2节中的理论分析，本文分别考虑位置稳定概率、上传数据量大小和分流节点个数对分流时间的影响进行实验，并将100次实验结果取平均值用于实验结果展示.

a)位置稳定概率对分流时间的影响

图2 位置稳定概率对分流时间的影响Fig.2 Iinfluence of position stability probability on offloading time

图2描述了在3种分流节点选择策略中，终端设备的位置稳定概率变化对分流时间的影响.从图2 可知，上传数据的分流时间随终端设备的位置稳定概率增加而减少.这是因为当终端设备的位置趋于稳定时，通过分析公式(6)可知：当终端设备移动到其他网格的概率降低时，公式(13)对分流时间的计算的准确率提高，因而选择最优分流节点的的准确率提高，减少数据分流时间.另外，比较3种分流节点选择策略，MDP在优化分流时间的性能上一直优于Random和OSTO.这是因为如算法1中的步骤b)所示，MDP会考虑到终端设备位置的变化来选择分流节点.因此，即使当终端设备的位置稳定概率为0.1时，相比于Random和OSTO，MDP优化分流时间的效果仍能提高18%和22%.

b)上传数据量对分流时间的影响

图3描述了当上传数据量大小变化时，采用3种不同的分流节点选择策略分流数据得到的分流时间.从图3中可以看出，当上传的数据量逐渐增大时，分流时间也随之增大.这是因为，在公式(9)和公式(10)中，上传数据量的大小正向影响数据的分流时间.另外，相比Random、OSTO这两个策略，MDP在数据量逐渐增加时仍表现出了良好的性能，在分流时间的优化上相较于Random、OSTO分别提高了30%和70%.这是因为MDP在进行分流节点的选择过程中，综合考虑到终端设备可能移动的位置及上传的数据量大小的变化.根据公式(4)计算系统转换概率进而计算选择不同的分流节点上传数据的分流时间，最终通过值迭代算法选择能最小化分流时间的分流节点.而OSTO的分流时间均大于其余两个算法，这是因为OSTO优先选择支持WiFi通信的分流节点分流数据.在这种情况下，OTSO未考虑终端设备与分流节点之间的距离，这会导致由于距离太长而时延增大的问题，因此，OTSO的分流时间最长.

图3 数据量对分流时间的影响Fig.3 Influence of data size on offloading time

c)分流节点个数对分流时间的影响.

考虑到不同场景中微蜂窝基站和WiFi AP部署情况存在差异，在这一节中分别在WiFi AP：微蜂窝基站=1∶1，WiFi AP：微蜂窝基站=1∶2，WiFi AP：微蜂窝基站=2∶1这3种节点比例的环境下进行实验.图4、图5和图6分别描述了在不同的节点比例下，分流节点个数的变化对分流时间的影响.从3张图中可以看出，当分流节点的个数增多时,MDP分流时间呈下降趋势，而Random和OSTO这两种分流节点选择策略的分流时间平均是MDP的2-4倍.这是因为，从公式(2)可知，分流节点的增多会扩大MDP的状态空间，在进行分流节点选择时，MDP能进一步优化分流节点的选择，进而优化分流时间.因此当节点个数增多时，采用MDP分流策略得到的分流时间会减少.

当分流节点的比例变化时，从图4可以看出，当节点比例为1∶1时，Random和OSTO的分流时间随着分流节点的增多而增大.这是因为，当分流节点增多时，Random和OSTO可用来分流数据的分流个数增多.这增加了Random和OSTO选择分流节点的盲目性，使分流时间呈上升趋势.从图5可以看出，当节点比例为1∶2时，即：部署的WIFI AP个数少于微蜂窝基站个数时，Random算法优化分流时间的效果明显优于OSTO.这是因为，Random选择分流节点时不考虑分流节点支持的通信技术的区别，这增大了Random选出最优分流节点的概率，有利于提升优化分流时间的效果.从图6中可以看出，当WIFI AP节点个数多于微蜂窝基站个数时，OTSO优化分流时间的效果大幅度的提高.特别是当节点个数大于24

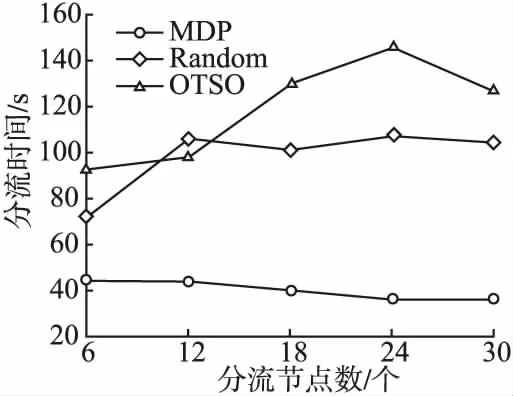
图4 节点比例为1∶1时分流节点个 数对分流时间的影响Fig.4 Influence of the number of offloading nodes on the offloading time when the node ratio is 1∶1

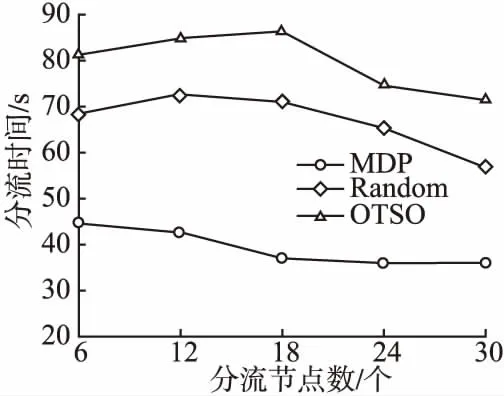
图5 节点比例为1∶2时分流节点个 数对分流时间的影响Fig.5 Influence of the number of offloading nodes on the offloading time when the node ratio is 1∶2

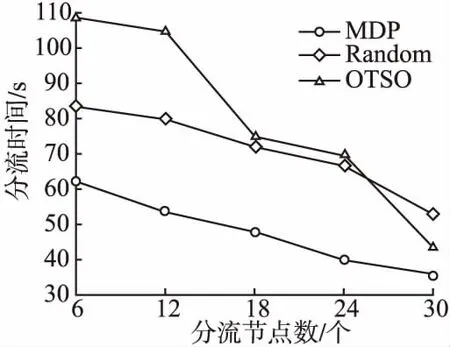
图6 节点比例为2∶1时分流节点个 数对分流时间的影响Fig.6 Influence of the number of offloading nodes on the offloading time when the node ratio is 2∶1

时，OTSO的最小化分流时间的效果优于Random.这是因为，当分流节点个数增多，WiFi AP：微蜂窝基站=2∶1时，边缘层中WiFi AP个数的增多能弥补OTSO在选择分流节点时不考虑通信距离的缺陷，并且由于WiFi的传输速率快，因此当WiFi AP个数增多时，优化分流时间的效果更佳.

5 结束语

本文研究了边缘计算中数据分流的问题，提出基于MDP的最优分流节点选择策略.本文通过考虑到数据量变化和终端设备的位置变化，将分流节点选择问题建模成MDP模型，并通过VIA算法求解模型，得到最优分流节点选择策略.大量实验结果表明，相比于Random、OSTO两个基准算法，本文所提策略在优化分流时间上的效果上的有效性.在未来的工作中，可以通过增加终端设备支持的通信技术(如：D2D通信)，综合考虑终端设备传输数据时的能耗和成本等其他因素进行更深入的研究.