Mn4+离子光谱学基础

姬海鹏

（郑州大学材料科学与工程学院郑州市先进能源催化功能材料制备技术重点实验室，河南郑州 450001）

1 引 言

目前，白光半导体发光二极管（LED）已在照明和液晶显示领域迅速取代荧光灯与白炽灯。蓝光LED 复合黄/红光荧光粉是获得白光的商业主流方案。对于白光LED 用荧光粉而言，一类重要的红色荧光粉是Mn4+激活氟化物，典型组分如K2SiF6∶Mn4+，已由美国通用电气公司成功商业应用，并引发了新型Mn4+激活荧光粉的研发热潮。

在研发新型Mn4+激活荧光粉时，应当选取何种元素组成及何种结构的基质？为什么被取代离子一般需要形成六配位八面体结构？Mn4+能否在其他配位环境（如五配位或七配位）中掺杂？Mn4+离子在氟化物基质（如K2SiF6）中表现出窄带发光，而在氧化物基质（如MgAl2O4）中常表现出宽带发光，这种现象应如何理解？当调节Mn4+离子的发射光谱时，什么情况下可望获得强零声子线发光，而又在什么情况下可以获得高能量光子发光？有时观察到多个零声子线发光峰，而有时声子振动伴峰发生了劈裂，这与什么因素有关？为回答上述问题、理解相关实验现象，需要了解Mn4+离子光谱学的基础知识。

Brik 教授、Adachi 教授等已撰写了一系列论文[1-7]对Mn4+离子光谱学做了深入介绍，但理解上述论文需要一定基础知识。本文尝试介绍这些基础知识。尽管这些知识中的大部分都在《高等结构化学》等相关书籍中有所述及，但本文更有针对性地阐述Mn4+离子相关的知识且给出详细推算过程，并讨论分析Mn4+离子的发光光谱，以期对刚进入该领域的科研工作者或工程技术人员提供参考。

2 Mn4+自由离子光谱项的求算

Mn4+离子的光谱项与其电子排布密切相关。锰的原子序数是25，根据核外电子排布三原则和递建原理（参考补充文件注释1 和2），确定其电子排布式为1s22s22p63s23p64s23d5，即[Ar]3d54s2，而Mn4+离子的电子排布式为[Ar]3d3。Mn4+的5 个d 轨道具有相同主量子数n（=3）和角量子数l（=2），其磁量子数ml（=±2,±1,0）不同（参考补充文件注释3）。每个轨道最多可容纳两个电子，如泡利不相容原理所述，这两个电子的自旋角动量必须相反，因此5 个d 轨道共可提供10 个单电子态。在这10 个单电子态中排列3 个电子，共有120 种不同方式（即C（10,3），参考补充文件注释4）。

用量子数n、l、ml可描述单个原子轨道的行为。对于多电子原子系统，则需要用原子的量子数S（总自旋角动量量子数）、L（总轨道角动量量子数）和J（总角动量量子数）来标记由于电子排布方式不同引起的不同组态以及由于电子的轨道与自旋的电磁相互作用下每种组态所包含的不止一种的能量状态。

考虑轨道-自旋相互作用，将总轨道角动量L与总自旋角动量S相加，得到总角动量J。有两种求算J的方法，一种是先把每个电子的s合并成S，l合并成L，再将S和L合并成J（该方法称为Russell-Saunders 偶合或简称L-S偶合）；另一种方法是先把s和l合并成j，然后再将j合并成J，称为j-j偶合[8]。

在L-S耦合中，原子的总轨道角动量量子数L等于每个电子的轨道角动量的矢量和（公式（1））；若一个电子的角量子数为l1，另一电子的角量子数为l2，其矢量和可由Clebsch-Gordan 数列（公式（2））给出：

原子的总自旋角动量S等于每个电子的自旋量子数的矢量和（公式（3））；两个电子的自旋量子数的矢量和也可采用Clebsch-Gordan 数列（公式（4））给出：

由于s=1/2，所以S的值只能是1 和0。当电子数为3 时，再用一次角动量偶合规则求得S=3/2，S=1/2，依此类推。这种两个电子自旋角动量的加和称为自旋角动量偶合，简称s-s偶合。

在L-S偶合（公式（5））中，其矢量和也可由Clebsch-Gordan 数列（公式（6））给出：

当L≥S时，J可取（2S+1）个数值；当L＜S时，J可取（2L+1）个数值。常用光谱项符号2S+1L（参考补充文件注释5）来描述多电子原子的某一运动状态。该符号左上角2S+1 称为光谱多重性。多数情况下，L和S的数值对能级影响较大而J影响较小；将J写在右下角所得2S+1LJ称为多重态，表示由于轨道-自旋相互作用使不同J的状态对应具有微小差别的能级。

对于Mn4+离子，由于自旋-轨道相互作用相比于非球对称d 电子间库仑作用可以忽略，因此适用L-S耦合求算光谱项。具有相同n和l的电子属于同科电子，根据“删除法则”[9]去除违反泡利原理的光谱项，最终经L-S耦合求算出8 个具有不同L和S的简并项，以2S+1L表示为基态光谱项4F、激发态光谱项4P、2G、2H、2P、2D（1）、2F、2D（2）。上述光谱项中上标“4”和“2”分别表示自旋四重态（S=3/2）和自旋双重态（S=1/2）；字母P、D、F、G、H 分别代表L=1，2，3，4，5；下标“（1）”和“（2）”用于区分两个2D 光谱项。

下面以4F 基态为例介绍求算过程：根据洪特规则，Mn4+离子基态电子构型如表1 所示；因此，L=3，在光谱项中用大写字母F 表示；S=3/2；J=L+S,L+S-1,…,|L-S|=9/2，7/2，5/2，3/2。因此，基态光谱项为4F，光谱支项为4F9/2、4F7/2、4F5/2、4F3/2。而当如表2 所示的另一种电子态时，L=4，对应地用字母G 表示；S=1/2；J= 9/2，7/2。因此，该电子态的光谱项为2G，光谱支项为2G9/2、2G7/2。

表1 d3组态在基态构型时的电子态Tab.1 Electronic state of a d3 ion at the ground state

表2 d3组态的另一种电子态Tab.2 Electronic state of a d3 ion at an excited state

各光谱项的简并度为（2S+1）×（2L+1）。因此，4F 的简并度为4×（2×3+1）=28；类似地，4P 的简并度为12，2P 的简并度为6，2D（1）和2D（2）的简并度为10，2F 的简并度为14，2G 的简并度为18，2H 的简并度为22。上述光谱项的简并度之和等于120。

3d 电子间的库仑作用能使得这些光谱项具有不同的能量；经计算，Mn4+自由离子各光谱项的能量可用含有Racah 参数A、B和C（参考补充文件注释6）的表达式表示[2]，列于表3。从表3 可见，2P和2H 光谱项能量相等（偶然地）；各光谱项中均含有3A数值项，这是因为Racah 参数A反映d 轨道电子库仑作用能的各向同性部分，而B和C反映d轨道电子库仑作用能的各向异性部分。当只关注各光谱项间的能量差时，可忽略该3A项并设定4F基态的能量为零。对于Mn4+自由离子，Racah 参数B0为1 160 cm-1，C0为4 303 cm-1；当Mn4+掺入晶格后，受电子云膨胀效应（Nephelauxetic effect，参考补充文件注释7）影响，Racah 参数B和C将有所减小；减小的幅度主要由Mn4+与配体所成键中共价键/离子键的比例决定，同时也受所成键的键长和键角的一定影响。

表3 d3离子各光谱项的能量Tab.3 Energies of the free ion LS-terms of the d3 configuration

Mn4+自由离子各光谱项及部分低能量光谱项的精细图如图1 所示。

图1 Mn4+自由离子的光谱项能级：（a）全部能级；（b）部分低能量能级。Fig.1 Energy levels of a free Mn4+ ion：（a）the overall levels，（b）the several low-lying levels.

3 Mn4+离子光谱项在八面体晶体场中劈裂形式的群论求算

如图2 所示，在八面体晶体场中，Mn4+的5 个d轨道将产生能级分裂：dz2和dx2-y2轨道（这两个d轨道电子云“叶瓣”直接指向配体离子）能量升高，称为eg（“e”表示二重简并，其下标“g”表示偶，源于德语gerade，下同）；而dxy、dyz和dxz轨道（这三个d 轨道电子云“叶瓣”指向配体离子间隙）能量降低，称为t2g（“t”表示三重简并）。这三个能量降低的轨道有利于Mn4+三个d 电子占据而保持稳定，因此解释了Mn4+常需要在八面体晶体场中掺杂；在研发新型Mn4+激活荧光粉时，被取代离子需形成八面体配位结构。因此，一些报道Mn4+在四面体格位掺杂的文献如制备SrAl2O4∶Mn4+荧光粉[10]，是值得质疑的。此外，也有少量文献报道在不等价取代时，被取代离子可不形成八面体配位结构，如Wu 等[11]报道在K2NbF7中掺杂Mn4+，其中Nb5+与7 个F-离 子 形 成 多 面 体；而Deng 等[12]报 道，在KTeF5中掺杂Mn4+，其中Te4+与5 个F-离子形成多面体。上述eg与t2g间的能量差称为Δo，下标“o”表示八面体。为了保持分裂前后d 轨道的能量重心不变，t2g轨道比分裂前能量降低2/5Δo，而eg轨道比分裂前高3/5Δo。当用量子力学在配体作为点电荷近似下，按照晶体场理论进行准确计算可得：

图2 （a） 八面体配位时d 轨道与配体离子的相对位置示意图；（b）八面体晶体场中d 轨道的能级劈裂。Fig.2 （a）Orientation of the five d-orbitals with respect to the ligands of an octahedral complex.（b）Crystal field splitting of the d-orbitals in an octahedral field.

3d3组态所形成的多个光谱项将在晶体场中进一步劈裂为一定数量的新的能级，劈裂形式取决于Mn4+所处晶体场的对称性，且可由群论这一数学工具求算。下面介绍由群论求算Mn4+各光谱项在八面体晶体场中的劈裂。八面体配合物具有Oh对称性，为简单起见，先用O点群进行分析。O点群只有旋转对称操作和5 个不可约表示（即A1、A2、E、T1、T2），其特征标列于表4（每一点群的特征标表可在教科书中查询）。Oh和O点群的差别是前者有对称中心i而后者没有；因此Oh点群有10个对称类，即A1g、A1u、A2g、A2u、Eg、Eu、T1g、T1u、T2g、T2u（补充文件中附表1 列出了Oh点群的特征标表，供参考）。

表4 中所列对称操作元素和左列所示多重态的含义，参见补充文件注释9 和10。

表4 O 点群的特征标表Tab.4 Character table for O point group

为求算一个有（2L+1）简并度的光谱项在八面体场中的劈裂，首先要定出一个具有轨道角动量量子数为L的原子状态进行一个旋转操作的特征标。已证明，绕z轴转动α角度的特征标χ为

对于其他对称操作元素，有

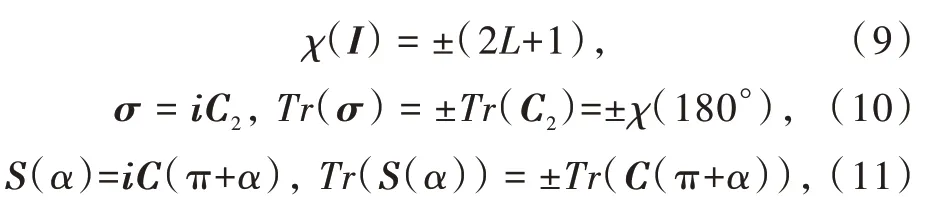
对于公式（10）和（11），当χ（i）为正时，取“+”运算符；当χ（i）为负时，取“-”运算符。

此外，在全同操作E中，α=0，有

由上述公式可计算任意L值的谱项在O点群中各种对称操作的χ值；进一步地，用这些χ值和O群的特征标表，按公式（13）可推导出不可约表示：

其中，n=Nelement，即对称操作元素的总数量；求和符号内为经公式（8）～（12）计算得到的可约表示与特征标及相应对称操作元素数量的乘积。

下面以P 谱项（L=1）为例说明求算过程。由公式（12）可得

由公式（8）～（11）可得

由公式（14）～（17）计算结果可得P 谱项在O点群的可约表示如表5 所示。然后再按公式（13）推导其不可约表示，算得n（A1）=n（A2）=n（E）=n（T2）=0，n（T1）=1；因此，P 谱项在O点群劈裂，由群论算出的不可约表示为T1。而相比于O点群，在Oh点群中还存在映轴Sn等对称操作，计算更复杂；因此，本文还以F 谱项为例，给出其在Oh点群不可约表示的详细求算过程，见补充文件注释8。

表5 P 谱项在O 点群中的可约表示Tab.5 Reducible representation of a P term in the O point group

类似地，逐一计算出P 谱项以外的其他各谱项在O点群中的不可约表示，汇总于表6。此外，在与O点群相比而对称性更低的晶体场中时，各光谱项的简并度进一步降低，直到所有的能级都变为单重态。

表6 Mn4+离子光谱项在O 点群中的劈裂Tab.6 Splitting of Mn4+LS terms in the O point group

对于d3电子组态的Mn4+离子，由上述过程已定出其各光谱项在八面体晶体场中有哪些劈裂能级存在，那么这些光谱项的具体能级图是怎样的？1954 年，日 本 物 理 学 家Tanabe 和Sugano 对Orgel能级图进行改进，提出了Tanabe-Sugano 能级图，给出了不同晶体场强度下各光谱项的劈裂情况[14]。图中横纵坐标不采用能量绝对单位（例如cm-1），而用Racah 参数（即电子排斥参量），同时用一根水平线来代表基态能级。如前所述，自由离子 谱 项 的 能 量 可 由Racah 参 数A、B和C表 示，而相同的电子组态dn的各谱项的A部分相同，且C≈4.5B，因此各谱项的间隔取决于B。因此，采用B为能量单位，则每个dn图就变得普遍适用了（可用于电子组态相同、配位体不同的各种金属配合物），不再只适用于建构dn组态图的某一特定离子。图3 为d3离子在八面体晶体场中的Tanabe-Sugano 图（C/B=4.5）。横坐标为Dq/B，纵坐标为E/B，都是无单位量。将4A2g基态视为0 eV，可用实测荧光光谱中4A2g→4T2g和4A2g→4T1g激发跃迁与2Eg→4A2g发射跃迁的零声子线（Zero Phonon Line，ZPL）能量，通过公式（18）～（20）计算Dq与Racah参 数B和C[15]：

图3 八面体场中d3离子的Tanabe-Sugano 图（图中灰色虚线左右分别为弱和强晶体场作用区；激发光谱中常见的两个激发峰对应于从基态到蓝色箭头标识出的两个激发态间的跃迁，红色箭头所示为从最低激发态2E 到4A2基态间的跃迁）Fig.3 Tanabe-Sugano diagram for the d3 electron configuration in the octahedral crystal field（The gray dashed line divides the weak and strong crystal fieldregions；the arrows in blue indicate the two excited states to which the ground state would be excited to，corresponding to the two bands that generally observed in the excitation spectra；the arrow in red indicates the transition from the lowest excited state2E to the ground state4A2）

其中，ΔE等于E（4T1g（4F）ZPL）-E（4T2g）ZPL。实际计算时，很多文献做如下简单近似，即将4A2g→4T2g跃迁带峰值所对应能量视为E（4T2g）而求得10Dq，将4A2g→4T1g和4A2g→4T2g两跃迁带的峰值的能量差视为ΔE而由公式（19）求算出B，再将发射跃迁的E（2Eg）ZPL能量代入公式（20）求算出C。但有时上述近似处理误差过大而得到显著异常的Racah 参数，因此需要4.5 小节所述方法确定各跃迁的ZPL 能量。

在氟化物基质中，4A2g→4T1g跃迁与F-→Mn4+电荷迁移带跃迁彼此不重合；但在氧化物基质中时，4A2g→4T1g跃迁与O2-→Mn4+电荷迁移带跃迁常重合在一起，因而有文献误将该电荷迁移带跃迁归属为4A2g→4T1g跃迁。理论上，Mn4+掺入晶格中后其Racah 参数B不可能大于其为自由离子时的B0，因此，一些文献中将电荷迁移带跃迁误认为4A2g→4T1g跃迁而求算出错误的B和C。此外，对光谱进行了错误的跃迁归属也将导致求算得到或异常小或异常大（比如大于5～6）的Dq/B值。

4 Mn4+激活荧光粉的荧光特性与荧光光谱

Mn4+掺杂进入基质晶格后将得到能量不同、形状各异的荧光光谱。接下来讨论如何理解这些光谱。

4.1 荧光光谱中激发与发射跃迁的归属

在 图3 所 示 的Tanabe-Sugano 图 中，10Dq/B≈20 处是第一激发态改变的临界点。当10Dq/B＞20时，其激发光谱由4A2g→4T2g（4F）和4A2g→4T1g（4F）两个宽带自旋允许跃迁组成。经无辐射弛豫后，由2Eg激发态经自旋禁戒跃迁回4A2g基态得到发射光谱。当10Dq/B＜20 时，激发光谱仍然由上述两个自旋允许跃迁构成，但此时发射光谱由4T2g→4A2g自旋允许跃迁得到。对于Mn4+离子而言，由于其正电荷数较多，常受强晶体场作用（Tanabe-Sugano 图中10Dq/B＞22～25），因此其发射光谱总是来自于2Eg→4A2g自旋禁戒跃迁（而同为d3离子的Cr3+，则可或经受强晶体场或经受弱晶体场作用，第一激发态发生变化而表现出或窄带或宽带或窄带和宽带同时出现的发射光谱）。第三个自旋允许的吸收带源自4A2g（4F）→4T1g（4P），其具有更高的能量（＞40 000 cm-1或5 eV）。该跃迁吸收带由于与配体离子（如O2-）→Mn4+电荷迁移带跃迁（宇称允许跃迁）吸收重叠，因此在激发光谱中难以清晰识别。当Mn4+局域环境的实际对称性低于八面体时，自旋三重态（T 态）会进一步劈裂，从而导致吸收带中出现亚峰。激发带的宽度受Mn4+的电子态与晶格振动间的电子-振动相互作用的强度影响，可由位形坐标模型解释。在位形坐标模型中，4A2g能级（t32g电子构型）与4T2（g4F）和4T1（g4F）两个激发态能级（t22ge1g电子构型）的势能曲线不在同一平衡位置而是相差ΔR0。在基态和激发态中，分布着不同的离子晶格振动能级；根据量子力学关于谐振子能级和出现几率的解，谐振子出现几率虽然在R0处最大，但在R=R0的两边也有一定的概率分布（而当温度升高时，谐振子将处于较高的振动能级，且出现几率最大处不在平衡位置R0而是在势能曲线的边界上）。根据Franck-Condon 原理，因电子的质量比离子的质量小很多，在电子跃迁的瞬间，离子无法及时调整位置，晶体保持位形不变，电子在两个静止的位形曲线间竖直跃迁。在低温下，光学跃迁发生在基态的ν=0 振动能级到激发态的振动能级ν′之间，由于谐振子在R=R0的两边也有一定的概率分布，因此所得激发光谱为宽带，且峰值出现在基态ν=0 振动能级的平衡位置R0到相应激发态ν′振动能级的跃迁处。

2Eg→4A2g发射跃迁对应于单个电子的自旋翻转，表现出较弱的电子-声子耦合。根据群论，对于Oh点群的八面体而言，有6 种基本振动模式，即ν1（A1g）、ν2（Eg）、ν3（T1u）、ν4（T1u）、ν5（T2g）和ν6（T2u）；而只有2Eg→4A2g跃迁与反对称振动模式ν3（不对称伸缩）/ν4（不对称弯曲）/ν6（不对称弯曲）耦合时（ν3/ν4/ν6振动模式示意图见补充文件附图1），宇称选择定则才能得到解除。因此，测得的发射光谱以含有零声子线（其强度因Mn4+的局域配位八面体的畸变程度不同而不同）与声子振动伴峰的3个Stokes（位于ZPL 右侧）和3 个anti-Stokes 线（位于ZPL 左侧）为特征。声子能量从大到小依次为ν3、ν4和ν6振动模式。在Mn4+激活氟化物中经常观察到线状振荡结构发射峰；而在Mn4+激活氧化物中却观察到宽带发射峰（指零声子线和/或振荡峰结构不明显，尤其是在室温或高温时），比如MgAl2O4∶Mn4+发射峰的半高宽可高达1 744 cm-1[16]，但其仍来自于2Eg→4A2g跃迁，而发射峰类似宽带的原因可能是由于ν6振动模式出现声子伴峰（Phonon replica of ν6vibration）或类似效应[17]。

4.2 Mn4+荧光寿命较长的原因

Mn4+激活荧光粉表现出较长的荧光寿命，一般在2～9 ms（室温）之间。这是因为2Eg→4A2g跃迁同时被宇称选择定则和自旋选择定则所禁戒。2Eg→4A2g跃迁属于d-d 跃迁。当配合物具有Oh点群，对该点群特征标表的研究说明一个电偶极允许的跃迁必须是“g”态（中心对称）和“u”态（反对称）间的跃迁，即要符合Laporte 选律。由于d 轨道是中心对称“g”态，不可能发生电偶极允许跃迁；实验中观察到d-d 跃迁，是由于电子运动和分子振动间相互作用即振动的波函数和电子的波函数混杂引起的。定性地看，电子跃迁发生在配合物的振动瞬间，这些振动破坏了分子的对称性；当这种振动发生时，状态失去“g”特性，使电子跃迁变成了少量的宇称允许。

除宇称选择定则外，还有自旋选择定则，即相同自旋态间的跃迁（ΔS=0）是允许的。自旋禁阻跃迁如ΔS=±1 所观察到的强度很弱，约为允许跃迁的百分之一。自旋-轨道耦合作用使得可观察到自旋禁阻的2Eg→4A2g跃迁[2]。自旋-轨道耦合作用使得2G 和4F 谱项内具有相同总角动量J的能态间彼此混合[2]，这种少量的混杂使得ΔS=0 选律不再完全适用。

因此，在实验中观察到Mn4+离子2Eg→4A2g这种同时被宇称选择定则和自旋选择定则所禁戒的跃迁对应的发射；但其从激发态返回基态的过程与Eu2+离子这种d→f 电偶极允许跃迁（荧光寿命0.6～1.0 μs）显著不同，表现为毫秒级长荧光寿命。将Mn4+掺杂在具有畸变八面体配位的氧氟化物基质中制备混合阴离子化合物荧光粉是一种获得短荧光寿命的途径[18]。

4.3 Mn4+在氟化物中呈现线状发射光谱的原因

Mn4+激活氟化物红光荧光粉在液晶显示背光源领域应用时，在显色色域和色纯度方面优于Eu2+激活氮化物红光荧光粉，主要得益于前者为主峰位于～630 nm 的线状发射光谱而后者是主峰波长更长的宽带发射光谱。比如，商用K2SiF6∶Mn4+荧光粉表现出具有类似振荡结构的6 个线状发射峰，每个发射峰都很窄（半高宽＜5 nm），分别对 应 于ν6、ν4和ν3振 动 模 式 的Stokes 和anti-Stokes发射峰。Mn4+激活氟化物荧光粉表现线状发射光谱，是因为Mn4+经受强晶体场作用，其荧光发射来自2Eg→4A2g跃 迁，而2Eg与4A2g能 级 都 来 自 于t32g电子构型。在位形坐标模型图中，两能级势能曲线平衡位置的差ΔR几乎等于0，电声子耦合强度很弱，且由图3 可知，2Eg能级几乎不随晶体场强度的变化而变化，电声子耦合对该能级的位置几乎没有影响。因此，Mn4+表现出与三价稀土离子（如Eu3+）f-f 跃迁相类似的线状发射光谱。

4.4 发射光子能量的影响因素

如图3 所示，尽管2Eg能级与x轴几乎平行，几乎不受晶体场强度影响，但实际可观察到Mn4+在不同化合物中的发射波长在617 nm（如Na2SiF6∶Mn4+[19]）到740 nm（如La4Ti3O12∶Mn4+[20]）非常宽的范围变化。在不同基质中Mn4+离子d 轨道受电子云膨胀效应的影响不同，影响程度和Mn4+与配体所成键的离子键/共价键比例有关；这种化学键由成键离子波函数重叠而成，该重叠在不同晶格间变化很大，主要取决于配体的种类与电负性（由此可解释Mn4+在氟化物和氧化物基质中发射能量的差异，Mn4+的2E 能级在氟化物中的能量总是高于其在氧化物中的能量[2]），也受化学键长短和键间夹角的影响（由此可解释Mn4+在不同氟化物或氧化物间发射能量的差异）。

当Mn4+所处格位形成正八面体即Mn4+的d 轨道与配体的p 轨道在同一轴线时，可预期其2Eg能级将有较大幅度降低，因为此时两轨道波函数间重叠最大，导致Racah 参数B和C较大程度的减小。而当Mn4+所处格位形成畸变八面体或八面体间彼此倾斜排列时，Mn4+的d 轨道与配体的p 轨道波函数间重叠减少，电子云膨胀效应减弱，导致Racah 参数B和C减小程度降低，因此2Eg发射能量相对较高[21]。在畸变八面体中，由于晶体场对称性降低，二重态能级2Eg可进一步劈裂，此时劈裂形成的具有最低能量的那个单重态能级成为新的发射能级；由此，可在几十到上百波数范围内进一步调节发射峰的能量[21]。

2016 年，Brik 等[21]引入了一个新的参数β1来定量描述电子云膨胀效应：

相比于β=B/B0，该参数考虑了掺入晶格后不止Racah 参数B还有参数C的减小。由此，对大量Mn4+激活氟化物和氧化物荧光粉的2Eg能量与β1绘图得到了二者间较好的如下线性关系：E（2Eg→4A2g）=-142.83+15544.022β1，且绝大多数数据都落在该拟合线上下均方根差σ=365 cm-1范围内（该σ值接近于常见的声子能量）。该线性关系可在一定程度上辅助验证所求算的Racah 参数与E（2Eg）是否合理。

此外，当受外部压力时，原子间距缩短，导致Mn4+离子d 轨道与配体离子p 轨道间波函数重叠增加，电子云膨胀效应增强，Racah 参数减小，2Eg→4A2g跃迁能量降低，波长红移。在基质晶格中进行固溶组分设计也能实现上述效果，比如用半径更大的阳离子部分替换基质晶格中的阳离子，则将对近邻Mn4+—配体所成键产生压力（可称为“化学压力”），使之缩短而产生与前述施加外部压力同样的效果。不同之处在于，施加外部压力是对晶格中所有化合键产生作用，而固溶掺杂则只对其最近邻配位键产生作用。

4.5 零声子线的确定

（1）2Eg→4A2g发光跃迁的零声子线。根据Mn4+掺杂基质的不同，在其发射光谱中，可能观察到2Eg→4A2g跃迁的ZPL，也可能观察不到。绝大多数情况下，Stokes ν6发射峰的强度高于ZPL 和anti-Stokes 发射峰；少数情况下，如在具有较大畸变八面体配位的氧氟化物和氟化物中（如Na2WO2F4∶Mn4+[22]、Ba2HfF8∶Mn4+[23]），ZPL 强度高于ν6发射峰。而在ZPL 强度很低时，较难准确地确定其位置。

最直接确定ZPL 的方法是对比低温和高温荧光光谱。低温时声子布居减少，电声子耦合变弱，常温时看不到的ZPL 将可能会在低温下出现且线宽比声子伴峰更锐。作为一个示例，图4 给出了Na2SnF6∶Mn4+在20～440 K 的变温发射光谱。随着温度降低，在617 nm 处逐渐出现了一个发射峰且其强度随温度降低而逐渐升高，应为ZPL 发射峰；位于其高能侧的610 nm附近的发射峰表现出从低温到高温逐渐出现并强度增强的特征，可判定为anti-Stokes 声子伴峰；位于其低能侧的627 nm 处的发射峰，随温度升高，强度呈规律变化且逐渐宽化，符合Stokes 声子伴峰随温度变化的特征。

图4 Na2SnF6∶Mn4+荧光粉在20～440 K 温度范围内每隔20 K 所测变温发光光谱（λex=470 nm）［24］Fig.4 Temperature-dependent photoluminescence emission spectra of Na2SnF6∶Mn4+ between 20 K and 440 K in increments of 20 K（λex=470 nm）［24］

一种间接确定ZPL 的方法是根据Stokes 与anti-Stokes 声子伴峰关于ZPL 呈对称分布的特征来确定。作为一个示例，图5 给出了NaKSiF6∶Mn4+在能量尺度下的发射光谱。在16 120 cm-1（620 nm）处有一发射峰，其高能和低能侧各有两个发射峰彼此对称，分别距离该峰219 cm-1，为[MnF6]基团的常见振动能量；此外，在该峰左右两侧还有另外两个对称分布的发射峰，分别距离该峰345～348 cm-1，对应于[MnF6]基团另外一种振动模式的能量。因此，可判定16 120 cm-1处为ZPL 峰。

图5 NaKSiF6∶Mn4+荧光粉的发射光谱［2］Fig.5 Emission spectrum of NaKSiF6∶Mn4+［2］

（2）4A2g→4T1g和4A2g→4T2g等 激 发 跃 迁 的 零 声子线。4A2g→4T2g跃迁是Mn4+激活荧光粉中的一个主要的激发吸收跃迁，高于该能量还可发生4A2g→4T1g,a（4F）、4A2g→2A1g、4A2g→2T2g、4A2g→2T1g和4A2g→4T1g,b（4P）等跃迁以及电荷迁移带跃迁（CTB）。因此，4A2g→4T2g跃迁之外的另一个高能激发跃迁带常常很宽且强度较高，很难对其进行准确的跃迁归属，可简单地认为另一个高能激发跃迁来自于4T1g,a（4F）和/或CTB/4T1g,b（4P）能级。

为确定4A2g→4T2g和4A2g→4T1g,a（4F）跃迁的零声子线，日本群马大学Adachi 教授提出，在位形坐标模型下，根据Franck-Condon 原理，实验所测得的每一激发跃迁带可视为一定数量的跃迁峰的组合；每一个跃迁峰来自于某一个激发态振动能级与某一个基态振动能级间的跃迁。因此，可采用公式（22）对每一跃迁对应的激发带进行谱峰拟合[17]：

其中，σex是每个高斯分量的展宽能，Iex0为ZPL 强度。对K2SiF6∶Mn4+激发光谱的研究表明，在20 K时，4A2g→4T2g跃迁带表现出明显的周期性齿状跃迁峰结构（图6（b）），将这些跃迁峰之间的间隔定义为hνp,ex，其约等于65 meV，该值与Mn4+所掺杂基质的种类几乎无关，且等于[MnF6]2-基团具有拉曼活性的ν2振动模式的能量。进一步地，为简单起见，认为σex趋近于0，则公式（22）所描述的IPLE线状激发可用公式（23）所描述的泊松概率分布函数体现：

其中，S是平均局域振动数，即Huang-Rhys 因子，该值越大，电-声子耦合越强。图6（b）、（d）为用公式（23）对激发光谱中的3 个或4 个激发跃迁带拟合后的结果。比如，对于图6（b）所示K2SiF6∶Mn4+的激发光谱，经公式（23）拟合后得到如下ZPL 能量，即E（4T2g）ZPL=2.68 eV（S= 2），E（4T1g,a（4F））ZPL=3.20 eV（S= 6），hνp,ex=65 meV。

图6 （a）位形坐标模型内激发与发射跃迁示意图；（b）K2SiF6∶Mn4+荧光粉在20 K 时的激发与发射光谱（各跃迁的ZPL 位置用虚直线标出）［25］；（c）位形坐标模型（含电荷迁移带势能曲线，即CTB）内激发与发射跃迁示意图；（d）Mn4+激活氧化物荧光粉的典型激发与发射光谱（各跃迁的ZPL 位置用虚直线标出）［17］。S = Stokes；a-S = anti-Stokes.Fig.6 （a）Configurational coordinate model representing photoluminescence emission and excitation transitions.（b）Emission and excitation spectra of the K2SiF6∶Mn4+ phosphor at 20 K（The positions of each transition were pointed out by dashed lines）［25］.（c）Configurational coordinate model（with parabolic band for charge-transfer band，CTB）representing photoluminescence emission and excitation transitions.（d）Schematic representation for the typical emission and excitation spectra of the Mn4+-activated oxide phosphor（The positions of each transition were pointed out by dashed lines）［17］. S=Stokes；a-S=anti-Stokes.

此外，在Mn4+激活氟化物荧光粉中，尚未观察到任何与2T1g相关的激发与发射峰，因此无法准确确定其能量位置，但一般地，可认为其在2Eg能级上～0.1 eV 处。类似地，在Mn4+激活氟化物荧光粉中也尚未观察到任何与4A2g→2T2g相关的激发与发射峰。但如图6（d）所示，在Mn4+激活氧化物荧光粉中，有时观察到4A2g→4T2g和4A2g→4T1g,a（4F）跃迁之间的一个小峰，可归属于4A2g→2T2g跃迁。由上述拟合方程可类似地确定这些激发跃迁的ZPL位置。

但需注意到，由于同一荧光粉在不同温度下所得激发光谱的形状（如半高宽、相对跃迁强度等）也不同，因此，采用公式（23）拟合低温和常温所得各跃迁的ZPL 能量及S值将有所不同；而针对氧化物荧光粉，由于其激发光谱非常复杂，且在液氦温度下也较难观察到像氟化物那样清晰的周期性齿状跃迁峰结构，因此通过上述方程拟合求解ZPL 能量时，4A2g→4T1g,a（4F）跃迁的ZPL 相比于4A2g→4T2g和2Eg→4A2g跃迁的ZPL 更难准确确定（因为实测光谱中高能量跃迁带可能是多个能级跃迁的叠加）[5]。考虑到Racah 参数C/B比值一般在4.2～4.9 之间，或可直接假定为4.7[5]，则可利用更易准确确定的Dq和E（2Eg）ZPL值来求算B和C，计算公式为将公式（19）和（20）加以改造后的公式（24）和（25）：

最后，Adachi[5]将大量已报道氟化物荧光粉的E（2Eg）ZPL（在1.996±0.020 eV 范围）和氧化物荧光粉的E（2Eg）ZPL（在1.838±0.100 eV 范围）与相应计算出的Racah 参数B作图后，发现经最小二乘法拟合，可以得到很好的线性拟合结果，即E（2Eg）ZPL=0.0027B-0.030 eV。该拟合公式也可用于验证由实验光谱计算所得Racah 参数的合理性。

4.6 Mn4+发射光谱在低格位对称性下的劈裂

在图4 所示的荧光光谱中，实际上可见两个ZPL 峰且ν6等声子伴峰也发射了明显劈裂。作为一个示例，如下讨论Zhu 等[26]报道的K2TiF6∶Mn4+的发光光谱。当Mn4+掺入K2TiF6中时，其取代具有D3d格位对称性的Ti4+格位，该对称性低于Oh。如图7（a）所示，根据群论，在D3d对称性格位时，Mn4+各光谱项相比于其在Oh格位将进一步发生劈裂；此外，在考虑自旋-轨道相互作用后，2Eg和4A2g能级都又进一步劈裂成两个次能级（将来自于2Eg的两个劈裂能级跃迁回4A2g基态的两个发射峰标记为R1和R2）。如图7（b）所示，在3～30 K 极低温条件所得各发射峰的半高宽都非常窄，利于进行跃迁归属。在30 K 时，622.08 nm 和621.70 nm 处的两个发射峰可分别归属为上述R1和R2跃迁。按照前述群论推断，因2Eg和4A2g能级各劈裂成两个次能级，而应该观察到4 个ZPL，但当前只观察到R1和R2两个，可能是4A2g能级的劈裂能级间的能量差非常小，当前光谱仪无法清晰分辨。随着温度继续降低，如低至3 K 时，只能观察到R1发射峰而R2消失，这是因为2Eg能级劈裂形成的高能态次能级在极低温下热布居减小（Thermal de-population）。此外，可见ν6、ν4和ν3声子伴峰发生了明显劈裂。根据群论，具有Oh对称性的八面体基团具有6 种内部振动模式，即ν1（A1g）、ν2（Eg）、ν3（T1u）、ν4（T1u）、ν5（T2g）和ν6（T2u）；当格位对称性从Oh降低为D3d时，三 重简并的ν3、ν4、ν5和ν6模式将进一步劈裂为一个二重态和一个单重态[27]。而可与ZPL 跃迁耦合的振动模式有反对称的ν3（T1u）、ν4（T1u）和ν6（T2u）。因此，图7（b）中630.81 nm 和631.98 nm 处 的 两 个 峰 可 归 属 于2Eg→4A2g+ν6跃迁，634.68 nm 和635.98 nm 处的两个峰可归属于2Eg→4A2g+ν4跃迁，而646.10 nm 和646.85 nm 处的峰可归属于2Eg→4A2g+ν3跃迁。而在图7（c）中所示的从R1线偏移0～400 cm-1范围内的其他弱发射峰，则来源于外部晶格振动模式（External lattice vibronic modes）与ZPL 耦合产生的跃迁。

图7 K2TiF6∶Mn4+的精细发光光谱。（a）Mn4+离子在D3d对称晶体学格位时能级劈裂的推导；（b）K2TiF6∶Mn4+（0.72%）荧光粉在460 nm 激发下在3～30 K 温度范围内的精细发光光谱；（c）在3 K 时从R1线偏移（以R1的能量为零）0～400 cm-1范围内弱发射峰的放大显示。星号标记的峰是与2Eg的高能态亚能级耦合的发射［26］。Fig.7 High-resolution electronic and vibronic spectra of K2TiF6∶Mn4+.（a）Deduced energy level splitting of Mn4+ ions at a crystallographic site of D3d symmetry.（b）Emission spectra of K2TiF6∶Mn4+（0.72%）measured at 3-30 K on 460 nm excitation.（c）Enlarged weak emission peaks at 3 K in the range of 0-400 cm-1 shifting from the R1 line（the energy of R1 is set to zero）.The peaks indicated by asterisks are the residual emissions coupled to the upper sublevel of2Eg［26］.

因此，当Mn4+所取代格位的对称性低于Oh时，将发生ZPL 以及声子伴峰的劈裂。实测发光光谱中观察到的劈裂情况取决于受群论制约的理论劈裂、光谱测试时的温度以及光谱仪的分辨率。当Mn4+处于不同的低对称性格位时，ZPL（和声子伴峰）理论上应发生什么样的劈裂、ZPL 劈裂数量与格位对称性间是否有固定对应关系，目前尚未见详细综述。

5 总结与展望

本文从Mn4+离子的电子排布开始介绍，先后给出了求算Mn4+离子光谱项的过程和利用群论工具求算各光谱项在八面体晶体场中能级劈裂的过程，使读者对Tanabe-Sugano 图的由来更加清晰。基于上述对Mn4+离子相关知识的介绍，以理解Mn4+激活荧光粉的荧光光谱为目标，进一步就Mn4+离子跃迁选律、激发与发射光谱的跃迁归属、影响发射光子能量的因素、零声子线的识别以及发射光谱劈裂与晶体格位对称性的关系等方面进行了分析讨论。

当前Mn4+激活红光荧光粉的研发遇到瓶颈，笔者期望未来有学者就Mn4+离子光谱学开展深入探讨以辅助新型高效荧光粉的研发。例如，（1）Mn4+激活荧光粉应用于蓝光LED 时，其蓝光吸收效率是决定外量子效率的关键。位于蓝光区的4A2g→4T2g跃迁虽然为自旋允许跃迁，但d-d 跃迁为宇称禁戒跃迁，导致吸收效率较低（相对于d-f允许跃迁）；此外，相比于Mn4+激活氟化物荧光粉，大多时候，Mn4+激活氧化物在蓝光区的激发光谱强度显著低于其在紫外光区的激发强度，除了在氧化物中4A2g→4T1g跃迁与宇称允许的电荷转移跃迁重合外，是否有其他原因解释该现象？如何通过部分破除宇称禁戒选律使d-d 跃迁几率提高（比如将Mn4+掺杂在畸变八面体中）或者通过优化制备工艺提高Mn4+激活氧化物中Mn4+的掺杂浓度且维持4+价态，进而提高荧光粉的蓝光吸收效率，值得深入研究。（2）商业用K2SiF6∶Mn4+的主发射峰位于630 nm，来自于Stokes ν6发射峰；如果主发射峰从630 nm 移至620 nm，则人眼视觉敏感度可提高～10%，因此有必要研发强ZPL 发光的Mn4+激活荧光粉。在什么晶格畸变或格位对称性条件下可望实现ZPL 显著强于ν6发光强度，是否有某种理论指导基质的选取，值得探讨。

本文补充文件和专家审稿意见及作者回复内容的下载地址：http://cjl. lightpublishing. cn/thesisDetails#10.37188/CJL.20220102.