考虑地基-桩基-结构共同作用的轴流压缩机组基础动力特性
熊 晔 丁 扬 査吕应 陈孜孜 刘洋武
(军事科学院国防工程研究院,北京 100089)
伴随着国民经济的稳步增长,交通、工业、市政等基础设施的建设进入了高潮,桩基础作为一种常见的基础形式,也得到了广泛的应用。在民用建筑中,桩基础一般承受静力荷载,桩基的承载力和基础沉降往往是人们关注的对象。而对于一些工业设施,如动力设备基础、风力发电机基础等,除了要考虑静力荷载作用下桩基础的承载力和沉降问题,还要对动力荷载下的桩基动力特性进行分析。针对动力设备基础的动力特性,如何考虑地基-桩基-结构共同作用,是工程界重点关注的问题。
轴流压缩机是工业设施中重要的动力设备,通常采用框架式基础,轴流压缩机在运行时对基础产生扰力作用,由扰力产生的基础振动位移对轴流压缩机的正常运行有一定的影响,因此,需要对轴流压缩机基础的振动位移响应进行研究。梅德庆等提出了汽轮发电机框架式基础的动力学模型,通过试验与有限元分析,发现基础底板厚度对框架式基础的动力特性影响较小[1-2]。徐朝刚等考虑了汽轮机框架式基础与地基的相互作用,计算得到了汽轮机基座振动线位移的频幅曲线,并分析了振动线位移与结构振型存在的关系[3]。张福铜研究了地基刚度对基础振动线位移的影响[4]。代泽兵等采用有限元计算和模型试验分析研究了燃气轮机组基础的动力特性[5]。刘宝泉采用SAP2000与TGFP分别模拟了汽轮发电机框架式基础,计算了扰力作用下的受迫响应分析,考虑了动力机器-基础-地基的共同作用[6]。金培豪通过石油化工特种构筑物软件SCAD对河南骏化项目6 743 kW离心式压缩机构架式基础进行了计算,考虑了不同构件截面对振动速度和振幅的影响,但并未考虑地基-基础-结构的共同作用[7]。
可见,考虑地基-桩基-结构共同作用是压缩机组基础动力特性研究的关键。因此,拟通过有限元程序对双桩承台基础的振动线位移进行模态和稳态分析,并利用现场双桩承台基础的动力特性试验结果加以对比,以验证考虑地基-桩基-结构共同作用的有限元分析方法的合理性。在此基础上,进一步对压缩机组基础进行有限元模拟,计算基础顶板的振动线位移,并研究模态阻尼比、桩径和桩长等因素对轴流压缩机组基础的振动线位移的影响。
1 动力机器动力特性研究方法
1.1 动力学的基本分析理论
结构体系的无阻尼自由振动的运动方程为:

(1)

结构振动特征方程:
([K]-ω2[M]){φ}={0}
(2)
式中:ω、{φ}为结构的频率和振型向量。
通过该方程可以求得结构的主各振型φi以及其对应的频率ωi,i为第i阶振型号。
在谐荷载作用下,结构体系的动力学问题可以表示为在惯性力作用下的静力平衡方程:

(3)

在谐荷载作用下结构体系的位移响应可以表示为:
{X(t)}={A}sin(ωt+θ)
(4)
式中:{X(t)}、{A}、ω和θ分别为结构的位移向量、位移幅值向量、荷载频率和位移响应滞后于谐荷载的相位角。
1.2 相关技术标准的规定
目前,关于动力设备基础的动力响应计算,一般将地基与桩基础通过弹性边界进行模拟,GB 50040—2020《动力机器基础设计规范》[8]和美国标准ACI 351.3R-04均规定了天然地基与桩基的动刚度和其阻尼比等动力特性参数的计算方法,间接地考虑了桩与地基对结构的影响,但并没有充分地反映地基-桩基-结构的共同作用。
1.3 考虑地基-桩基-结构共同作用的模拟方法
对基于模态的稳态分析,是一种隐式求解方法,在计算过程中,模型边界不存在应力波的反射问题,当地基范围选取足够大时,通常可直接设置固定边界。基于有限元程序,建立考虑地基-桩基-结构共同作用的计算模型,模型中地基、桩基与结构均通过实体单元进行模拟,地基、桩基和结构之间的接触均采用绑定接触,并且在地基的边界处设置法向约束。在此基础上对动力设备基础的振动位移响应进行稳态分析。为验证该方法的合理性,通过双桩承台原位模型试验对有限元计算结果进行验证对比,在验证模型合理的基础上,进一步模拟压缩机组基础的动力特性。
2 双桩承台原位模型试验的有限元模拟
双桩承台原位试验所在位置位于压缩机组拟建场地附近,该场地的地层由第四系全新统人工填土层、第四系全新统坡积层以及下伏的白垩系下统剑阁组泥岩和砂岩构成,各地层的岩性分述如下:①素填土层,主要为全风化泥岩、粉质黏土含有少量植物根系,土层厚度为0.3~3.5 m;②强风化泥岩,主要矿物成分为黏土矿物,泥质结构,土层厚度为0.4~11.3 m;③中风化泥岩,主要矿物成分为黏土矿物,泥质结构,土层厚度为2.6~22.8 m;④中风化砂岩,节理裂隙发育,砂质结构,土层厚度为0.3~5.5 m。场地岩土层、桩基和承台混凝土的物理参数如表1所示。试验中双桩承台的布置如图1所示,承台厚度为2.0 m,桩径为600 mm,桩长为15 m,桩端持力层为中风化泥岩,桩身和承台的混凝土强度等级为C30。

表1 土层与混凝土材料物理参数Table 1 Physical characteristic indexes of soil and concrete

图1 双桩承台基础布置 mmFig.1 Arrangements of foundations with double piles
依据GB/T 50269—2015《地基动力特性测试规范》[9]的规定,试验仪器主要由组合式中型机械偏心式激振系统、拾振器和记录仪三部分组成(图2),试验中机械激振器的最大激振力为60 kN(70 Hz),主要测试双桩承台基础在埋置状态下的强迫振动。每组双桩承台基础受到竖向振动、水平回转振动和扭转振动三种工况。试验得到竖向振动、水平回转振动和扭转振动工况下对应的阻尼比(表2)和双桩承台基础的振动幅频响应曲线。

图2 试验装置Fig.2 The test device

表2 各工况实测阻尼比Table 2 Measured damping ratios in various working conditions
对试验的双桩承台基础,建立有限元模型(图3),单元类型为C3D8R。各部件之间假定采用绑定的接触形式,主要是考虑桩长范围内的地基主要为中风化泥岩,有较好的刚度,桩基采用钻孔灌注桩,桩基浇筑成形时,桩体与桩周泥岩能很好地咬合嵌固在一起,基本符合绑定接触的假设;承台与土体的接触也近似按绑定接触设置,主要考虑在激励器作用下,承台基础的位移很小,承台与土基本能够协调变形。

图3 双桩承台基础有限元模型Fig.3 The finite element model of the foundations on double piles
模型中仅对受扰力作用下的桩承台基础赋予质量属性,其余桩承台基础和土体部分均采用无密度单元。如此假定主要考虑以下两点:一是土体弹性模量与混凝土差别很大,而密度相近,在进行模态分析时,几乎都是土体的局部振动,无法获得桩承台基础振动位移,这种土体的局部振动对桩承台振动位移为无效振型,振型叠加后,土体的局部振动对承台的扰力振动位移几乎无影响,因此为了能在较少的振型范围内获得桩承台的主要振型,只考虑了土体的弹性作用;二是考虑到不受扰力的桩承台的参振质量对扰力桩承台的振型及自振频率很小,而其振动相对受扰力的桩承台来说同样为局部振动,对扰力作用下桩承台的振动位移贡献不大。
通过模态分析得到该模型的各阶振型,前六阶振型为整体振动(图4),六阶振型以后均为局部振动。

图4 双桩承台基础各阶模态频率分布Fig.4 Modal frequencies of the foundation with double piles
截取前六阶振型进行稳态分析,计算双桩承台基础的振动位移响应。双桩承台基础振动位移的有限元解与试验实测值的对比如图5~7所示。图5中,在竖向扰力作用下,有限元模拟在70 Hz下振动产生的位移峰值,结果表明与试验结果较为接近,有限元解略大于试验结果。图6中,在水平回转扰力作用下,有限元模拟在45 Hz附近产生位移峰值,有限元解略小于试验结果。同样,如图7所示,有限元模拟与试验结果位移响虽然在位移峰值上存在略微差异,但与其幅频曲线的峰值位置与曲线形态吻合较好。因此,有限元模拟方法得到的结果与试验得到的振动位移幅频分布规律基本一致,较好地模拟了双桩承台基础的动力试验,证明了该有限元模拟方法的合理性。

a—有限元解;b—1号基础实测值;c—2号基础实测值;d—3号基础实测值。图5 双桩承台基础竖向振动位移幅频曲线Fig.5 Curves between vertical displacement amplitudes and frequencies of the foundations with double piles

a—有限元解;b—1号基础实测值;c—2号基础实测值;d—3号基础实测值。图6 双桩承台基础水平回转振动位移幅频曲线Fig.6 Curves for horizontally rotary displacement amplitudes and frequencies of foundations with double piles

a—有限元解;b—1号基础实测值;c—2号基础实测值;d—3号基础实测值。图7 双桩承台基础扭转振动位移幅频曲线Fig.7 Curves between torsional displacement amplitudes and frequencies of foundations with double piles
3 轴流压缩机组基础动力特性分析
3.1 分析模型与动力荷载
某轴流压缩机组基础为混凝土框架式基础,其结构类型为单层混凝土框架结构,基础采用桩筏板基础。动力基础梁柱截面尺寸按设计取值,桩径为0.6 m,桩长为18~24 m,框架式基础筏板长×宽为24 m×9 m,厚度为2.5 m。轴流压缩机基础的有限元模型如图8所示,各部件之间采用模型中实体单元均采用C3D8R。土体的长×宽×深度范围为80 m×70 m×50 m,并在边界处设置法向约束,忽略边界的黏弹性特性。桩基及筏板的材料特性见表3,地基土的材料特性同双桩模型试验。在模型中,仅对桩基、筏板和结构部分赋予质量属性,其余部分均采用无密度单元。

表3 基础和地基土材料特性指标Table 3 Material characteristic indexes of foundations and foundation soil

图8 考虑地基-基础-结构共同作用有限元模型 mFig.8 The finite element model considered interaction of foundation,pile foundations and superstructures
轴流压缩机组基础主要扰力荷载来源于为轴流压缩机和电机,轴流压缩机和电机的工作转速均为2 100 r/min(工作频率为35 Hz)。基础受到的扰力作用点和附加质量点如图9所示。各点附加质量和工作转速下扰力幅值见表4,对于任意转速下的扰力表示按如式(5)进行计算。

图9 基础附加质量与扰力作用点布置Fig.9 Arrangements for additional masses and action points of disturbing forces on the foundation

表4 附加质量和工作转速下扰力幅值统计Table 4 Statistics for disturbing force amplitudes of additional masses at the working rotation rate

(5)
式中:P0i与Pgi分别为第i个扰力作用点处任意转速n0和工作转速下的扰力幅值。
3.2 基于模态的稳态分析
着重研究其前8阶振型,振型图如图10所示。前三阶振型主要是基础顶板的水平振动和扭转振动,第四阶振型为基础整体的竖向振动,而第五、六阶振型为基础底板的水平振动,第七阶振型为基础整体的竖向振动,第八阶振型为基础底板的扭转振动。很明显,第五、六阶振型和第八阶振型主要是基础底板的振动,对基础顶板的振动线位移的影响不大。

a—一阶振型(频率3.572 5 Hz);b—二阶振型(频率4.075 1 Hz);c—三阶振型(频率5.311 1 Hz);d—四阶振型(频率13.689 Hz);e—五阶振型(频率16.981 Hz);f—六阶振型(频率17.737 Hz);g—七阶振型(频率18.188 Hz);h—八阶振型(频率22.921 Hz)。图10 轴流压缩机组基础部分振型Fig.10 Vibration modals of the flow compressor foundation
在模态分析的基础上,对轴流压缩机组基础模型进行稳态分析,计算动力设备从启动到工作转速运行时,轴流压缩机组基础扰力作用点的振动位移。对于混凝土框架式动力设备基础,结构阻尼比可以取为0.062 5[8]。通过基础动力稳态分析,基础顶板的最大线位移发生在轴流压缩机支座点部位,见图9中A点。
图11为扰力作用下的轴流压缩机组基础顶板A点处的振动线位移响应。基础最大水平振动线位移为11.5 μm,而最大竖向振动线位移为10.6 μm。轴流压缩机组基础顶板的水平横向振动线位移和竖向振动线位移大于水平纵向振动线位移,在低频段,水平横向振动线位移起到控制作用,而在中间频段,竖向振动线位移起到控制作用。由图10、11可见:振动线位移稳态结果与模态分析的振型频率相对应,水平振动线位移在扰力频率为10 Hz以内达到峰值,对应于前三阶振型的自振频率,竖向振动线位移在13.7 Hz产生峰值,对应于第四阶频率的自振频率,而在基础底板振动的自振频率范围,基础顶板A点处的振动线位移很小。因此,对于框架式动力设备基础顶板的动力稳态分析,在简化计算时,一般可忽略基础底板与桩基的振动影响,即将其密度设为零。

图11 A点处的振动线位移响应Fig.11 Vibrational liner displacement response at point A
3.3 基础振动线位移的规律分析
在工程优化时,通常需要研究基础振动线位移的变化规律。从图11可以看出:轴流压缩机组在运行过程中,基础的水平横向振动线位移起到控制作用,以A点的水平横向振动线位移为研究对象,通过调整模型中模态阻尼比、桩径和桩长来研究轴流压缩机组基础的振动线位移随这些参数的变化,如图12~14所示。可见:模态阻尼比的变化对基础振动线位移影响较大,当模态阻尼比增大时,基础振动线位移峰值减小幅度较大,而基础振动线位移的频域分布变化很小。相比较而言,改变桩径对基础的振动线位移影响较小,随着桩径的增大,桩基础对上部框架结构的约束作用增强,结构模型前三阶振型的自振频率增大,与该振型发生共振的扰力幅值也相应增大,因此,随着桩径增大,基础的振动线位移也有较小幅的增大。从图14可见:当改变桩长时,基础振动线位移几乎不发生变化,通过增加桩长来增加基础嵌固深度,对改变框架式基础的振动线位移作用很小。

图12 不同模态阻尼比下的振动线位移Fig.12 Vibrational liner displacement in different modal damping rates
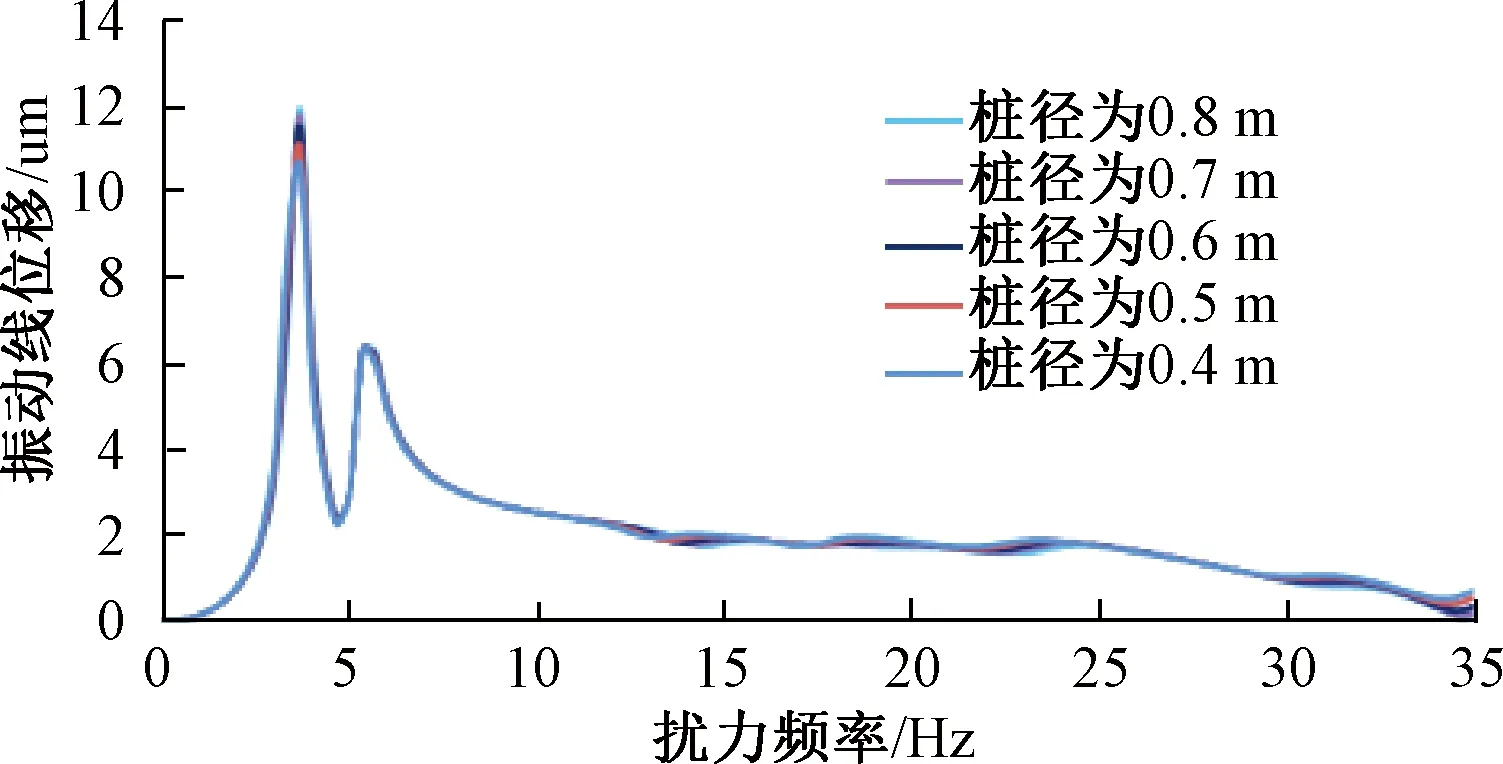
图13 不同桩径下的振动线位移Fig.13 Vibrational liner displacement in different pile diameters

图14 不同桩长下的振动线位移Fig.14 Vibrational liner displacement in different pile lengths
通过分析基础振动线位移的这几个主要影响因素可知,对于框架式动力基础,阻尼比对基础振动线位移的影响较大,在工程中设置合适的阻尼器可以有效减小基础振动线位移的幅值;而桩基的直径和桩长,对于基础振动线位移的影响较小,应根据桩基承载力和建筑物沉降的要求来确定。
4 结束语
针对考虑地基-桩基-结构共同作用的轴流压缩机组基础的有限元分析方法,通过双桩承台基础的试验对该方法的合理性加以验证。进一步对轴流压缩机机组基础顶板的振动线位移进行稳态分析,在此基础上,分析了轴流压缩机组基础振动线位移随模态阻尼比、桩长和桩径的变化规律。结果分析,得到结论如下:
1)采用实体建模对动力设备基础进行稳态分析,通过双桩基承台基础试验验证了该模拟方法是合理可靠的。
2)轴流压缩机组基础的水平横向振动线位移大于竖向振动线位移,基础的水平横向振动线位移起到控制作用。
3)基础顶板的水平振动线位移峰值发生在前三阶振型频率点附近,而竖向振动线位移的峰值,在第四阶振型的自振频率处发生,在机组基础设计时,动力机器的工作频率避开前四阶振型频率范围,可以有效减小振动线位移响应。
4)通过设置阻尼器,增加模态阻尼比,可以有效地减小基础顶板的振动线位移峰值;而调整桩基的直径和桩长,对基础的振动线位移影响较小。

