中美欧砌体结构设计与鉴定标准对比研究
吴乐乐 唐曹明,2 罗开海,2 程绍革,2 黄世敏,2
(1.中国建筑科学研究院,北京 100013;2.住房和城乡建设部防灾研究中心,北京 100013)
随着社会的发展,对老旧小区的合理加固和性能提升已经成为大的趋势。在老旧小区中,砌体结构占有相当大的比例,对其构件的安全性评估是不可或缺的一个环节。我国对既有建筑结构的安全性鉴定仍采用设计规范规定的极限状态表达式。设计规范中的极限状态表达式是针对新建建筑的,直接用于既有建筑的鉴定,是否合理值得深入研究。为此,有关学者和科研人员针对既有建筑相关的鉴定表达式、分项系数取值、荷载标准值以及目标可靠指标取值等方面开展了相关研究:Ellingwood认为既有建筑评估基于特定的工程背景,结构的失效概率是基于特定工况的条件概率[1]。由于作用和抗力的不确定性与设计时不同,极限状态方程中作用与抗力分项系数可以进行调整;Asp认为既有建筑的荷载和抗力不确定性因素低于新建建筑,极限状态方程的作用分项系数和抗力分项系数应小于新建建筑设计[2];Steenbergen从失效成本的角度考虑,认为既有建筑与新建建筑采用相同的目标可靠指标是不经济的,应根据后续使用年限进行调整[3]。顾祥林等根据适用于既有结构的荷载和抗力概率模型,给出了不同目标使用期楼面活荷载标准值取值,对不同目标使用期内的荷载分项系数进行了优化[4]。对永久荷载分项系数取值,当可变荷载控制时取1.0,永久荷载控制时取1.2,当效应对结构有利时取0.6;可变荷载分项系数取1.3,抗力分项系数根据受力构件不同取γR=1.0~1.8,并根据目标可靠指标增减0.25确定了既有建筑结构构件的等级评定标准。黄炎生[5]根据既有结构抗力与荷载的特点,建立了既有框架结构基于分项系数法的可靠性评估表达式,并根据可靠度校准法,将永久作用分项系数γG取1.2,可变作用分项系数γQ取0.814~1.168,抗力分项系γR根据目标使用期和受力构件不同,取1.114~2.266。李英民等以可靠性理论为基础,通过比较我国与美国住宅楼面荷载统计参数,以等超越概率为原则,建立了不同后续服役期内活荷载标准值与设计值之间的关系[6]。本文将对中、美、欧三个地区的砌体结构设计规范和鉴定标准进行综合比较,分析各国鉴定和设计方法、极限状态方程、分项系数设计方法的异同点,为今后有关鉴定标准的修订提供参考。
1 美国砌体结构设计规范与鉴定加固规范比较
1.1 美国砌体结构设计规范
ACI530BuildingCodeRequirementsandSpecificationforMasonryStructures[7]《砌体结构建筑规范要求和规定》对砌体结构采用允许应力设计和强度设计两种方法。允许应力设计方法基于弹性理论,需满足σ≤[σ],其中,[σ]=fu/K,K的取值较大且笼统,因此容许应力方法相对保守。强度设计方法,基于弹塑性理论,允许结构存在非线性行为。两种设计方法均采用ASCE 7-16MinimumDesignLoadsandAssociatedCriteriaforBuildingsandOtherStructures[8]《建筑和其他结构的最小设计荷载和相关标准》中规定的荷载组合如表1所示。其中强度设计方法中采用的极限状态方程如式(1a)所示。当活荷载控制时,采用强度设计方法的无筋砌体轴压构件,极限状态方程如式(1b)所示。标准轴压强度的计算方法如式(2)所示。规定无筋砌体的名义抗剪强度Vn取(3)~(7)赋值的最小值。
Sd≤φRK
(1a)
1.2D+1.6L≤0.6RK
(1b)
式中:Sd为作用效应;RK为砌体设计强度标准值;φ为强度折减系数。
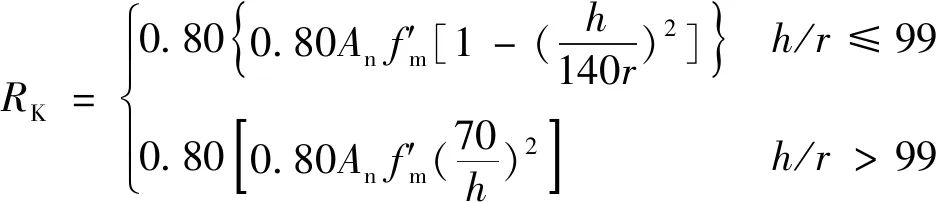
(2)
式中:An为砂浆净截面,f′m为砌体名义抗压强度;h为墙或柱高度;r为回转半径。
φ的取值反映了施工、材料特性、计算模型和预期失效模型的不确定性。对于强度设计方法:设计强度等于标准强度乘以折减系数φ;压弯组合时配筋砌体取0.9,无筋砌体取0.6;受剪时取0.8,轴压时取0.6。φ值越大,说明砌体强度计算值与试验值之比的变异系数越小,φ值越小,则变异系数越大。
名义抗剪强度Vn取值:
Vn=0.83An
(3b)
对错缝砌筑未灌实的砌体:
Vn=0.26An+0.45Nu
(4)
式中:Nu为抗剪面的设计压力。
对通缝砌筑端部开口砌块灌实的砌体:
Vn=0.26An+0.45Nu
(5)
对错缝砌筑灌实的砌体:
Vn=0.414An+0.45Nu
(6)
对通缝砌筑其他非端部开口的砌块灌实砌体:
Vn=0.103An
(7)

表1 ACI530荷载组合Table 1 Load combination of ACI530
1.2 美国砌体结构鉴定与加固规范
ACI318BuildingCodeRequirementsforStructuralConcrete[9]《混凝土结构建筑规范要求》规定,既有结构构件进行极限状态评估时,如果构件的尺寸、大小、位置和材料特性通过实地测量或试验获得,允许提高抗力的折减系数。如抗剪构件设计时,φ值为0.75,评估时则提高至0.8。受压构件设计时,φ值为0.65,评估时则提高至0.8。为此,在对砌体结构评估时,若相关的参数由现场或试验获得时,强度折减系数φ的取值,也可以相应地提高。
文献[8]规定的荷载适用于改建、扩建以及改变使用功能的既有结构。对既有建筑的评估和改造可以参照IEBC—2018InternationalExistingBuildingCode[10]《既有建筑国际规范》,其中规定对无筋砌体的强度可以采用现场实测强度,强度折减系数φ值为1.0。
ASCE 41-17SeismicEvaluationandRetrofitofExistingBuilding[11]《既有建筑抗震评估和改造》采用了基于性能的评估和加固改造方法。既有建筑的抗震评估和改造分为三级进行,第一级为筛选过程,第二级为基于缺陷的评估和改造过程,第三级为系统的评估和改造过程。第一级评估主要用于筛选出既有结构中的缺陷构件,第二级评估需要针对第一级的评估结果,采用线性静力方法(LSP)或线性动力方法(LDP)对缺陷部分进一步评估。在第二级评估时规范引入了认知系数к(Knowledge Factor к)进行构件强度折减。к 反映了对既有建筑信息收集的完整性和可靠性,同时也反映了对抗力认知的不确定性。第三级评估,采用系统性的评估程序,并根据信息采集情况考虑к系数。对于二级和三级评估分析方法,可以采用线性方法和非线性方法。对于线性分析,重力作用不利时QG如式(8a)所示,重力作用有利时QG如式(8b)所示,对于非线性分析,如式(8c)所示。
式中:QG为重力荷载代表值;QD为恒荷载;QL为活荷载;QS为雪荷载。
线性分析适用于规则结构或者满足需求能力比小于3.0的不规则结构。根据力-变形曲线的不同,可以将构件分为力控制构件和变形控制构件。在线性分析中,对于变形控制的构件需要满足式(9)的要求;对于力控制构件需要满足式(10)要求。
mκQCE>QUD
(9)
式中:m为承载力修正系数;κ为认知系数;QCE为预期承载力;QUD为作用需求。
κQCL>QUF
(10)
式中:QCL为构件承载力下限值;QUF为作用需求。
在非线性分析中,对变形控制构件,要求主要和次要构件的预期变形能力不得小于变形限值要求。对力控制构件,需要满足式(11)要求。
γχ(QUF-QG)+QG≤QCL
(11)
式中:QCL为构件的下限强度;γ为力控制构件荷载系数,对关键构件取1.3,非关键构件取1.0;χ为与结构性能相关的系数,性能目标为防止倒塌时取1.0,生命安全和立即入住时,取1.3。
对砌体结构的评估,认知系数κ是通过材料测试和条件评估的范围来确定。对于力控制砌体轴压构件,抗震承载力极限状态方程如式(12)所示,抗压强度下限值如式(13a)所示,抗剪承载力如式(13b)所示。
(12)
式中:QE为既定地震动水准下的地震作用;J为力传递折减系数;C1、C2为修正因子。
QCL=0.8(0.85f′mAn)
(13a)
式中:f′m为砌体现场实测强度;Vtest为砌体抗剪承载力实测值;Ab为砌体单元上下砂浆净面积和;PD+L为试验时的恒载加活载;PD为墙体上部恒载;An为砂浆净面积。
1.3 小 结
极限状态设计方程中抗力设计值采用强度标准值乘以折减系数φ的形式。砌体结构安全性评估时,抗力折减系数φ值比设计时提高,取φ=1.0。抗震评估规范采用了基于性能的评估方法,考虑了结构认知的不确定性,抗震设计与抗震评估的重力作用代表值与材料强度取值均不同。
2 欧洲砌体结构设计规范与鉴定加固规范比较
2.1 欧洲砌体结构设计规范
BS EN 1996-1-1∶2005 Eurocode 6 —DesignofMasonryStructuresPart1-1:GeneralRulesforReinforcedandUnreinforcedMasonryStructures[12]《砌体结构设计-第1-1 部分:有筋和无筋砌体结构的一般规则》采用BS EN 1990∶2002BasisofStructuralDesign[13]《结构设计基础》中规定的荷载组合。当采用承载力极限状态设计时,需满足式(14)的要求。其中文献[12]采用的基本组合形式如式(15)所示,地震作用设计组合形式如式(16)所示。BS EN 1998-1∶2004GeneralRules,SeismicActionandRulesforBuildings[14]《抗震结构设计-第 1 部分:一般规定、地震作用和建筑规定》中规定,地震作用时重力作用代表值如式(16)所示。
Ed≤Rd
(14)
式中:Ed为作用效应设计值;Rd为抗力设计值。
式中:γG,j为永久作用j的分项系数;γP为预应力作用分项系数;γQ,i为可变作用i的分项系数;ψ0,i为可变作用i的组合值系数;ψ2,i为可变作用i的准永久值系数;Gk,i为永久作用i的标准值;Qk,i为可变作用i的标准值;P为预应力作用的相关代表值;AEd为地震作用设计值。
G=∑Gk,j+∑ψE,iQk,j,ψE,i=φψ2,i
(16)
式中:ψE,i为可变作用i的组合值系数;φ计算系数。其他符号见文献[12-14]。
文献[13]中规定,当进行静力验算时,作用分项系数γG=1.35,γQ=1.5。因此,当仅考虑永久作用和一个可变作用时,极限状态方程如式(17)所示。对砌体轴压构件,抗压承载力设计值如式(18)所示。文献[12]中规定砌体材料分项系数γM取值与砌体的施工控制等级相关,在进行抗震承载力验算时γM取值不小于1.5。考虑水平地震作用下极限状态方程如式(19)所示,抗剪承载力如式(20)所示。
1.35Gk+1.5Qk,1≤Rd
(17)
式中:Gk为永久作用标准值;Qk,1为第一个可变作用标准值;Rd为抗力设计值。
(18)
其中φ=1-2ei/t
式中:φ为折减系数,与砌体长细比和偏心效应有关;t为砌体厚度;ei为偏心距;fk为材料强度标准值;γM为材料分项系数。
Gk+0.3Qk,1+Ehx+0.3Ehy≤Rd
(19)
式中:Ehx为水平地震作用x方向分量;Ehy为水平地震作用y方向分量。
(20)
式中:lc为受压部分长度;fvk0为初始抗剪强度(对于黏土砖,砂浆强度M5时,fvk0=0.30 N/mm2);σd为平均竖向应力。
2.2 欧洲砌体结构评估规范
ISO 13822BasesforDesignofStructures-AssessmentofExistingStructures[15]《结构设计基础:既有建筑评估》规定:在进行结构极限状态评估时,应当根据实际条件确定基本变量的概率模型,包括作用、材料特性和土工条件、构件的几何尺寸和基础形状以及模型的不确定因素等;可靠性评估应考虑现有结构的剩余使用寿命、基准期以及结构环境变化;由于经济、社会可持续发展等方面原因,既有结构评估的可靠性与新结构设计有很大的不同,在使用极限状态进行评估时,可以根据检测或试验的结果对随机变量概率分布进行校正。
忽略各基本变量间的相关性,可单独确定每个随机变量的校正设计值。对于抗力参数X其校正后的设计值xd如式(21a)、式(21b)所示。也可采用另一种方法确定xd,先确定标准值xk,再采用适当的分项系数γm计算设计值xd,如式(22)~(25)所示,一般k取1.645。由式(21)~(24)可知,当获得了校正后的概率分布且规定了既有建筑的目标可靠指标β时,即可获得对应可靠指标β条件的分项系数γd,如式(25)所示。

σ2=ln(1+V2)
(22)
xd=xk/γm
(24)
γd=xk/xd
(25)
文献[15]对既有结构评估基准期提出了建议:可采用预期的剩余使用年限作为既有结构评估基准期;对承载力极限状态评估,取较短的基准期更为合理。如有规定,目标可靠指标可按照现行规范选择,否则,可以选用表2中的值。荷兰标准NEN 8700AssessmentofExistingStructuresinCaseofReconstructionandDisapproval:BasicRules《重建和不批准的现有结构评估——基本原则》,在欧洲标准的基础上,根据评估基准期和服役期的不同对既有建筑改造和评估的最低可靠指标和荷载分项系数进行了调整,分别如表3和表4所示[16],其中ψ0为组合系数。

表2 目标可靠指标Table 2 Target reliability indexes

表3 最小可靠指标βTable 3 Minimum values for the reliability index β

表4 荷载分项系数Table 4 Load partial coefficients
BS EN 1998-3∶2005Eurocode8-DesignofStructuresforEarthquakeResistance-Part3:AssessmentandRetrofittingofBuildings[17]《结构抗震设计 第3部分:建筑物评估和加固改造》,采用了基于性能的评估和加固改造方法。结构的性能目标通过三种极限状态(LS)来定义,即几乎倒塌(NC)、严重损伤(SD)和有限损伤(DL)。根据对既有建筑的认知水平(反映了结构的不确定性程度,KL1—有限认知、KL2—一般认知、KL3—完整认知)的不同,分别规定了相应的置信系数CF(CFKL1=1.35、CFKL2=1.2、CFKL3=1.0)。进行性能评估时,材料性能取从现场实测的平均值除以置信系数。
对砌体结构进行评估时,需要对砌体结构的几何特性、构造、材料特性进行检测,并选定结构的性能水平。例如,对法向力和弯曲控制的构件,当选择进行SD状态验算时,所采用的砌体抗压强度设计值fd=fm/CF,其中fm是现场实测的抗压强度平均值,CF可取1.2。DL状态下,对弯曲控制构件,考虑水平地震作用下极限状态方程如式(26)所示。
Gk+0.3Qk,1+Ehx+0.3Ehy≤Vf
(26)
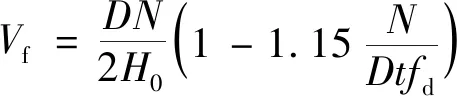
式中:Vf为地震作用下抗剪承载力;H0是计算抗弯承载力截面与反弯点截面之间的距离;D为墙体面内水平尺寸(高度);t为墙厚;N为轴向荷载。
2.3 小 结
既有建筑评估的基准期与设计时不同,进行评估时,采用较短的基准期更为合理,可根据实测统计结果对变量分布进行校正,根据校正后的变量分布和相应的目标可靠指标对分项系数进行修正。
荷兰标准根据评估基准期和服役期的不同对既有建筑改造和评估的最低可靠指标和荷载分项系数进行了调整。抗震评估采用基于性能的评估方法,考虑了既有建筑的认知水平,引入了置信系数。抗震设计与评估中极限状态方程作用效应组合相同,抗力计算方法不同。在设计中抗力采用标准值除以抗力分项系数的形式,而抗震评估中抗力是通过平均值除以置信系数的形式。
3 中国砌体结构设计规范与鉴定加固规范比较
3.1 中国砌体结构设计规范
GB 50003—2011《砌体结构设计规范》[18]规定,砌体结构按承载能力极限状态设计时,应按式(27)与(28)中最不利组合进行计算:
R(f,ak…)
(27)
(28)
对安全等级二级,设计使用年限为50 a,施工质量等级B级的砌体结构构件,取一个可变荷载和一个永久荷载时,如式(29)所示,抗力函数R(f,ak…)与砌体的强度设计值和几何参数有关。其中砌体的强度设计值f=fk/γf,fk=fm-1.645σf,fm为砌体强度平均值,施工质量等级B级时γf取1.6。
英译文:After going through a system of analysis,the Dou Qi rankings in the Dou Qi Continent got split into four different classes-Tian,Di,Xuan,Huang and every class was split further into Beginner,Medium and High ranks!
1.2SQk+1.4SQk≤R(f,ak…)
(29)
GB 50068—2018《建筑结构可靠性设计统一标准》[19]将可变作用的分项系数由γG=1.2,γQ=1.4,调整为γG=1.3,γQ=1.5,如式(30)所示。
1.3SQk+1.5SQk≤R(f,ak…)
(30)
对轴心受压构件的抗压承载力和抗剪承载力分别如式(31)、式(32)所示。考虑水平地震作用下,极限状态方程如式(33)所示,抗剪承载力如式(34)所示。
N≤φfA
(31)
式中:N为轴向力设计值;φ为高厚比β和轴向力的偏心距e对受压构件承载力的影响系数;f为抗压强度设计值;A为截面面积。
V≤(fv+αμσ0)A
(32)
式中:V为剪力设计值;A为水平截面面积;fv为抗剪强度设计值;α为修正系数;μ为剪压复合受力影响系数;σ0为永久荷载设计值产生的水平截面平均压应力,其值不应大于0.8f。
1.2(SGk+0.5SQ1k)+SEhk≤R/γRE
(33)
式中:SEhk为水平地震作用;R为结构构件承载力设计值;γRE为承载力调整系数。
V≤ξNfvA/γRE
(34)
式中:ξN为砖砌体抗震抗剪强度的正应力影响系数。
3.2 中国砌体结构鉴定标准
GB 50023—2009《建筑抗震鉴定标准》[20]根据不同的后续使用年限将既有建筑分为A类(后续使用年限30 a)、B类(后续使用年限40 a)、C类(后续使用年限50 a)。抗震鉴定分为两级。第一级鉴定应以宏观控制和构造鉴定为主进行综合评价,第二级鉴定应以抗震验算为主结合构造影响进行综合评价。
结构构件抗震验算公式如式(35)所示,抗剪承载力同式(34)。
S≤R/γRa
(35)
式中:S为结构构件内力组合设计值(遵循现行设计规范);R为结构构件承载力设计值(遵循现行设计规范);γRa为抗震鉴定的承载力抗震调整系数(一般按现行规范取值,A类建筑抗震鉴定时,钢筋混凝土构件取0.85γRE)。
GB 50292—2015《民用建筑可靠性鉴定标准》[21]规定,可靠性鉴定包括安全性鉴定和使用性鉴定。鉴定分为三个层次,如图1所示。对结构的鉴定或加固设计,结构上作用标准值均按GB 50009—2012《建筑结构荷载规范》[22]的规定,若实测值大于规范值则按实测值取值。加固设计时,根据下一目标使用期的不同可变作用标准值应乘以表5中修正系数。按检测结果确定构件材料强度标准值时,fk=mf-ks,此时k并不等于新建建筑取值的1.645(由于取值样本有限),而与概率分布下分位数a(取0.05)、检测所取得置信水平γ(对钢材取0.90,对混凝土和木材取0.75,对砌体取0.60)和样本数量n有关。
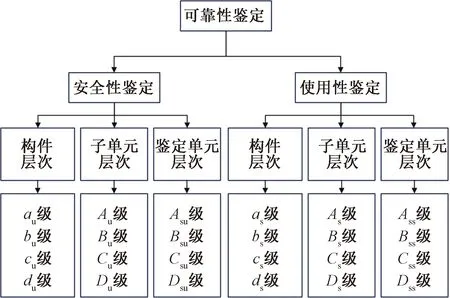
图1 可靠性鉴定分级Fig.1 Classification of reliability assessment
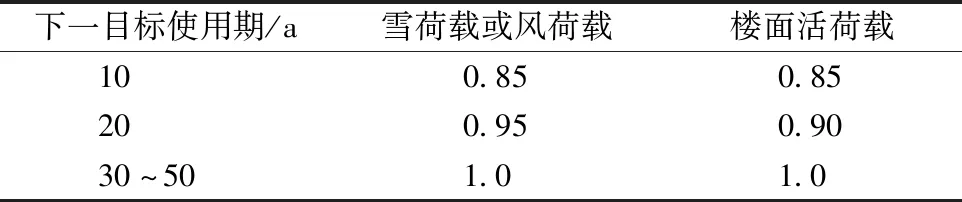
表5 基本雪压、基本风压及楼面活荷载的修正系数kaTable 5 Correction coefficients of basic snow loads,wind pressure and floor live loads
砌体结构构件安全性鉴定,应按承载能力、构造、不适于承载的位移和裂缝或其他损伤等四个检查项目分别评定,并取最低一级作为该结构的安全性等级。按承载力评定其安全性等级时,按表6确定,并取其中最低等级作为该构件承载力的安全性等级。按照墙、柱高厚比确定构件安全性等级,符合现行规范时取au级或bu级,超过文献[18]规定10%评定为cu级或du级。根据文献[21]的规定,可知表6中抗力和作用效应计算方式均与设计时取值相同。

表6 按承载能力评定的砌体构件安全性等级Table 6 Safety levels of masonry structures based on bearing capacity
DG/TJ 08-804—2005《既有建筑物结构检测与评定标准》[23],考虑了既有建筑的特点,重新定义了上海地区的基本雪压和基本风压值,并采用可靠性设计校准法,重新定义了结构的抗力分项系数。对于承载力极限状态验算时如式(36)所示。
γ0S≤R/γR
(36)
除γR外,γ0,S,R均按相关设计规范取值。γR根据构件受力状态的不同,取不同的值。其中砖砌体结构构件的抗力分项系数γR如表7所示。永久荷载分项系数取值,当可变荷载控制时取1.0,永久荷载控制时取1.2,当效应对结构有利时取0.6;可变荷载分项系数取值,一般情况取1.3,对标准值大于4 kN/m2的房屋楼面结构的活荷载取1.2。永久作用控制时,对于轴心受压构件,承载力极限状态按照式(37)进行。
1.0SGk+1.3SQk≤Rk/1.5
(37)

表7 砖砌体结构构件抗力分项系数γRTable 7 Resistance partial factor γR of the member of masonry structures
3.3 小 结
可靠性鉴定中,材料特性基于检测值。加固设计时,活荷载可以根据下一目标使用年限采用修正系数进行调整,抗力和作用效应的计算表达式均与设计相同。抗震鉴定标准中采用了二级鉴定模式,抗震验算的作用效应和抗力的计算表达式与抗震设计规范相同。地方标准中,对既有建筑鉴定的极限状态方程中,抗力和作用分项系数进行了调整。
4 三地区砌体结构设计与鉴定标准综合对比
三地区砌体结构设计与鉴定标准对比如表8所示。可知,设计规范中三个地区承载力极限状态方程中采用了不同的作用和抗力分项系数,这是由于三地区采用的分项系数确定方法不同;中国规范与欧洲规范采用校准法,二者分项系数不同是由于两个地区选取可靠水平不同;美国规范中的分项系数则是采用分离系数法,根据目标可靠指标确定。

表8 三个地区砌体结构设计与鉴定标准对比Table 8 Comparisons of design and assessment standards of masonry structures in three regions
对于既有结构构件的鉴定,美国标准采用的作用分项系数与设计规范相同,强度折减系数φ=1.0;欧洲标准则建议对作用和抗力分项系数分别进行重新校正,以更符合既有建筑的实际情况;荷兰标准则在欧洲规范的基础上,对既有建筑翻修和评估时的荷载分项系数进行了调整;中国标准采用的分项系数与设计规范相同。三地区的材料性能均采用实测值,但是取值标准有所不同,具有不同的材料强度保证率。在抗震鉴定中,美国和欧洲标准均采用了基于性能的鉴定方法,美国标准中对地震作用的选取考虑了性能水平的影响,材料性能基于实测强度的下限值;欧洲标准地震作用取值与设计相同,但抗力计算中考虑了性能水平的影响,引入了认知系数;中国标准中对基于性能的鉴定方法则没有详细的说明,抗震验算中采用的地震作用与设计相同,而地震承载力调整系数有所区别。
通过对比分析可以发现,中国鉴定标准中既没有降低作用分项系数,也没有降低抗力分项系数,与美国和欧洲鉴定标准相比,鉴定结论会相对保守。
5 结束语
美国鉴定标准强度折减系数φ=1.0(不进行强度折减),欧洲鉴定标准对承载力极限状态方程的分项系数调整方法做了明确的规定。美欧抗震鉴定,均采用了基于性能的抗震鉴定方法,根据对既有建筑认知水平的不同,美国标准引入了认知系数κ,欧洲标准引入了置信系数CF。同时,美欧标准调整了重力荷载代表值和抗震承载力的计算方法。中国鉴定标准采用与新建建筑设计相同的极限状态方程,没有针对既有建筑的特性进行分项系数修正,对既有建筑结构构件安全性鉴定相对保守。上海地方鉴定标准根据既有建筑特点采用校准法进行了分项系数修正,与欧洲鉴定标准的调整原则相一致。
随着科学水平的不断进步和工程经验的积累,鉴定标准必然会进行不断的修正和增加新的内容。本文认为以下方面需进行深入研究:
1)基于性能的鉴定方法。
2)既有建筑鉴定和加固时的目标可靠指标。
3)根据可靠性理论和既有建筑的特点,对鉴定极限状态方程中的分项系数进行修正。
4)根据可靠性理论对结构的安全性和使用性评价标准重新分级。从而在保证既有建筑结构安全可靠的同时又可以避免过度加固、从而减少对原结构的损伤。

