基于模糊时序网络的城市路网关键交叉口识别方法

李君羡，沈宙彪，童文聪，吴志周*

（1.同济大学，道路与交通工程教育部重点实验室，上海 201804；2.上海市城市建设设计研究总院（集团）有限公司，上海 200125）

0 引言

城市路网拥堵通常起因于少数关键交叉口通行能力降低，准确识别这些交叉口是针对性制定排堵保畅策略的前提工作，对保障城市路网可靠性有重要意义。

早期相关研究关注城市路网的几何拓扑结构，借鉴图论知识，将描述网络结构的基本参数如节点邻接度、介数等[1]作为识别路网关键交叉口的依据，或结合路网的特殊性，变换、改进上述参数[2]，补充交叉口其他特征如位置[3]、关联道路长度[3-4]等，使指标体系更适应交通问题分析。然而逐渐有学者认识到，相对于长期保持稳定的路网拓扑参数，交叉口的功能性是决定其关键与否更重要的因素。张诚等[5]考虑了路网流量-速度关系，提出基于空间流量度的多级流量加权关键交叉口识别模型；张建旭等[6]从路段失效的实际影响出发，综合出行者时间费用变化影响和局部路网路段交通负荷变化影响衡量路段重要度，也可作为关键交叉口识别的依据。近年来有研究突破基于单个交叉口特征开展重要性评价的局限，将交叉口的交互关系纳入考量，衍生出一系列基于特征向量中心性识别关键交叉口的方法。王灵丽等[7]将PageRank值[8]作为交叉口重要性指标之一参与关键节点决策，该指标借鉴自信息搜索领域，可体现网络中节点的权威性；类似地，冯慧芳等[9]基于交通流状态，结合有向加权复杂网络和DWNodeRank 算法对路网关键交叉口进行识别。这类算法反映出交叉口之间相互联系的本质，有较为成熟的理论背景，可解释性强，受到了普遍关注。

上述方法普遍基于静态网络模型，以某一时间步上集计的动静态参数作为依据评价交叉口重要性，忽略了城市路网运行状态的时序特征。实际上，城市路网是典型的时序网络[10]，交通运行参数时刻处于变化当中[11]且在连续时间步上存在关联。仅考虑路网拓扑及动力学过程识别关键交叉口丢失了重要的时间关联信息，结果普遍存在偏差[12]。尽管在其他领域，时序网络概念的出现很大程度上改进了静态网络关键节点识别的研究结果[10]，但鲜有文献将城市路网作为研究对象，综合路网的交通特性和时序特性以识别关键交叉口。

有别于仅关注城市路网结构和交叉口功能的网络分析模型，本文增加对路网时序特征的考虑，并结合交通参数的特征引入模糊性，搭建模糊时序网络模型以识别关键交叉口。首先，阐释一般时序网络的描述方法和经典超邻接矩阵（Supraadjacency Matrix,SAM）时序网络模型[13]的原理，分析其优势及其应用于城市路网关键交叉口识别所面临的局限；然后，通过引入时间步层内节点模糊关联指标和时间步层间相似性指标等方法克服以上问题，综合改进后的指标与算法搭建适用于城市路网关键交叉口识别的模糊时序网络模型；最后，以包含147 个交叉口的城市核心区域路网真实数据验证模型有效性，对交叉口重要性排名的统计特征、时序特性以及关键交叉口的空间分布特征展开分析，并测试模型敏感性。

1 SAM时序网络模型及局限性分析

1.1 一般时序网络描述

网络G包括有限节点构成的点集合V={v1,…,vm,…,vn,…,vN} 及这些节点对构成的边集合E，记作G=（V,E）,N为G中节点数量。一般时序网络将G的观察期间划分为T个等长时间步。若编号为m和n的节点vm、vn在时间步t存在交互，则产生一条三元组交互记录et=（m,n,t），对应连接vm、vn的一条边。按时间步集计所有交互记录生成的边，可将时序网络表示为离散的分层网络序列gT={G1,G2,…,Gt,…,GT} 。在此基础上，可构建SAM时序网络模型（简称SAM模型）。

1.2 SAM模型

构造任意gT的SAM模型，步骤如下。

Step 1 以N×N的邻接矩阵At表达Gt=（Vt,Et）中两节点的交互关系，即层内交互关系为

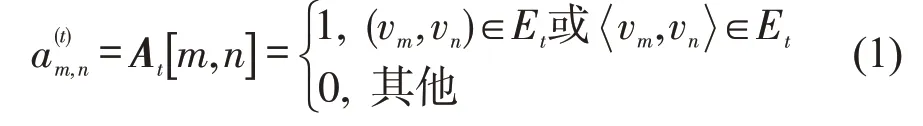
Step 2 以固定参数ω量化gT中两个相邻网络层Gt、Gt+1中所有对应节点的关联，即层间关联关系，关联越强则ω越大。

Step 3 综合层内、层间关系，构造描述该gT的SAM。SAM为（N·T）×（N·T）的分块矩阵，记作

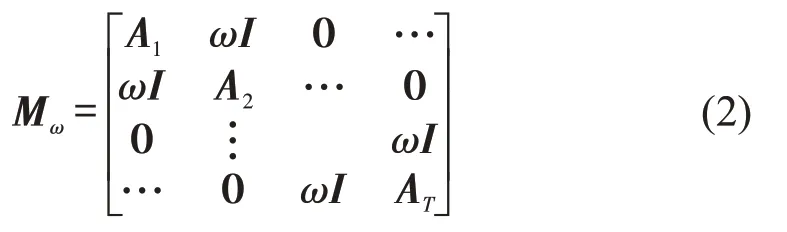
式中：I为N×N单位矩阵。以SAM描述时序网络从而识别关键节点的模型即为SAM模型。

SAM的主特征向量包含所有T个时间步中N个节点的特征向量中心性指标值，该值越大，该节点在相应时间步内重要性越高。据此可跟踪任一节点的中心性变化轨迹，达到识别时序网络关键节点的目的。SAM不仅考虑了同一时间步内不同节点之间的交互关系，也考虑了相邻时间步之间各节点特征的持续性，因此，SAM模型筛选出的关键节点兼具枢纽性和持续影响力，相对基于静态网络框架识别关键节点的方法有明显优势[13]，但将其用于城市路网关键交叉口识别则面临两个局限。

1.3 SAM模型的局限性

局限1 该模型对At的定义不适用于路网分析。根据式（1），At各元素以二进制数值表示网络中两个节点是否直接相连。而以交叉口作为节点、路段作为边所构成的路网拓扑结构长时间保持稳定，少见路段在完全通畅和完全失效两种状态下频繁切换的情况，导致该模型中的At失去了时序意义。自然地，基于描述路网功能的交通运行参数构造At较为合理，即认为两个交叉口的交互关系与连接它们的路段运行情况相关。但运行参数在规范化处理后多为指定区间内的连续值，可解释为交叉口层内连接关系的强度，相对于式（1）明确的二元值体现出一定模糊性。在此条件下，时序网络节点交互记录的形式应为，其中，为规范化的动态参数，需根据实际数据条件确定其计算方法。

局限2 该模型以同一个参数ω描述任意相邻网络层中所有节点的时序关联性，这与现实情况不符。首先，不同节点的时序关联强度往往存在差异，即使同一节点，其层间连接关系的强度也不尽相同；其次，ω的确定依赖主观判断，其取值极大影响最终的关键交叉口识别结果，导致算法不够稳定。

针对上述局限，提出两点优化措施改善SAM模型。

措施1 构造基于交通运行参数的交叉口模糊关联指标，以描述交叉口层内交互关系强度。

措施2 借鉴基于节点层间相似性的超邻接矩阵（Similarity-based Supra-adjacency Matrix,SSAM）时序网络模型[14]（简称SSAM 模型），引入邻居拓扑重叠系数并对其进行模糊优化，实现两相邻网络层间各交叉口关联强度的差异化表达。

2 模型优化

2.1 层内交叉口交互强度描述

针对SAM 模型的局限1，假设两交叉口Im、In以路段L直接相连，其间无其他交叉口。从功能性出发，定量描述时间步t中Im和In连接强度，可选用表征L交通负荷的运行参数，交通负荷越大则Im和In层内交互强度越大。以t期间的L平均行程速度（km·h-1）为例，有

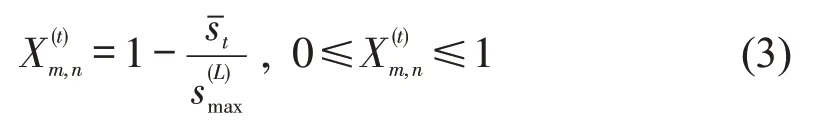
式中：为L自由流速度（km·h-1），可取路段限速或

由式（3），L流量较小时，大部分车辆可以接近的行程速度通过，此时接近0，Im、In交互强度较小；反之两交叉口交互强度较大，接近1。由此，层内交叉口交互强度被映射到[0,1]区间，有一定模糊性且在不同交叉口对之间、不同时间步上均有所区别。据此，构造层内交叉口交互强度矩阵A′t，其元素为

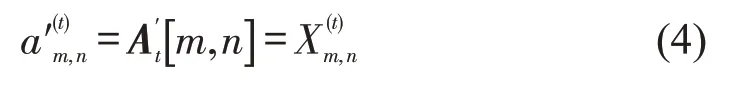
2.2 层间交叉口关联强度描述

针对SAM 模型的局限2，文献[14]引入层间相似性度量算法构造SSAM 模型，其核心是SSAM。SSAM 与SAM 结构类似，并同样以At表达层内交互关系，但以一个N×N对角矩阵，即层间关联强度矩阵C（t,t+1）代替对应位置的ωI，差异化描述相邻时间步t和t+1 的交叉口层间关联强度。，其中为

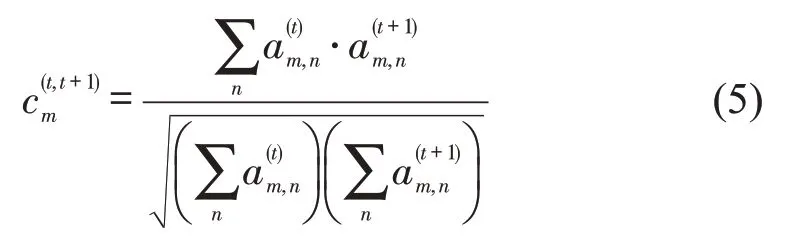
的定义借鉴了文献[15]中邻居拓扑重叠系数的概念，其含义为节点m在相邻网络中共同相连节点数量所占的比例。对于几何拓扑结构稳定的路网，C（t,t+1）显然不具区分作用，需对其进行优化。

仍然从交叉口功能性考虑，结合的算法对重新定义，以相邻网络上同一节点与其他节点的交互强度变化表征其层间交叉口关联强度，并选择余弦定理作为评价层间相似性的方法，即

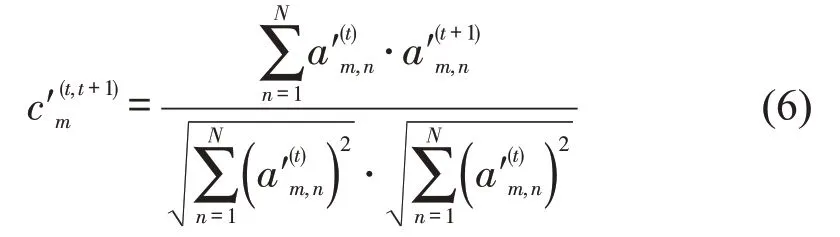
构成优化后的层间关联矩阵C′（t,t+1）=

2.3 模糊时序网络模型构建

综合A′t和C（t,t+1），按照式（2）构造适应路网分析的时序网络模型。鉴于时间步层内、层间关系的模糊性，称优化后的模型为模糊超邻接矩阵（Fuzzy Supra-adjacency Matrix,FSAM）时序网络模型（简称FSAM模型），其核心FSAM为

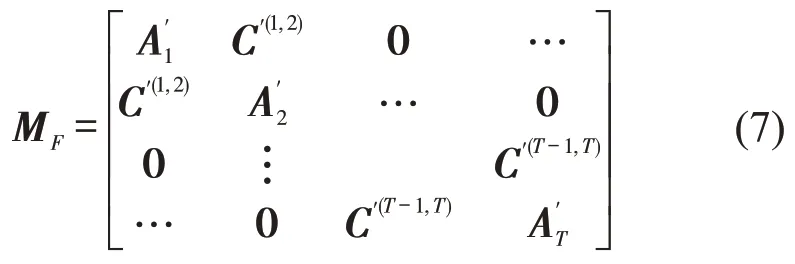
FSAM 的主特征向量包括时间序列上各交叉口的特征向量中心性指标信息，具备了SAM 的全面性优势，并可直接用于城市路网关键交叉口识别。

3 实例分析

截取某一线城市核心区域局部路网作为分析实例，其几何拓扑结构如图1所示。该路网统计特征值如表1所示。

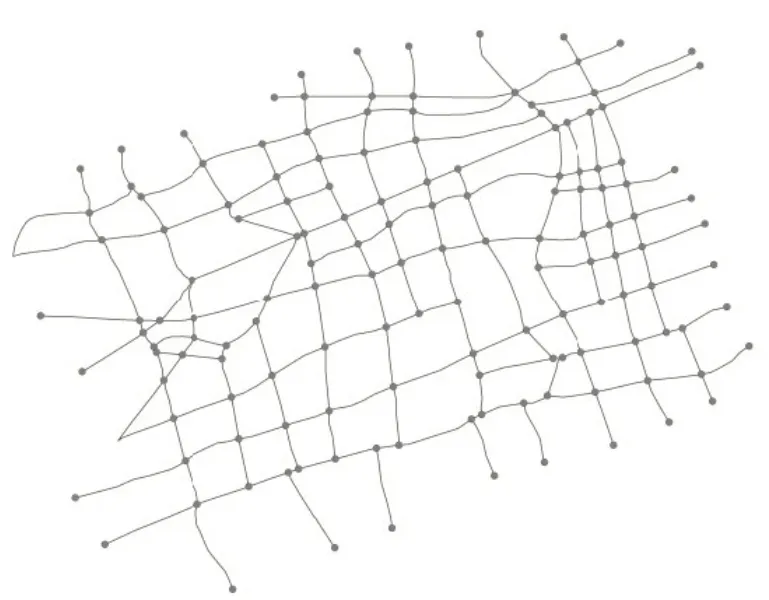
图1 实例路网拓扑结构Fig.1 Topology of example road network

根据表1，该路网lm不足300 m，交叉口分布密集。由于各路段均承担了较大流量，预期各交叉口重要性程度会随时间变化呈较大波动。以15 min为间隔，采集该路网某工作日全天共T=96 个时间步所有路段的平均行程速度数据。由式（4）计算所有时间步中任意相邻交叉口的交互强度并组合为A′t（1 ≤t≤T）；再由相邻A′t中的各个元素按式（6）综合计算所有节点对的层间关联强度，组合为C′（t,t+1）（1 ≤t≤T-1）；最后将所有矩阵按照式（7）组织为FSAM，计算其主特征向量，整理可得中心性指标时间序列W=[]w1,w2,…,wt,…,wT，wt为时间步t中所有节点的中心性指标值序列，将其排序即可识别该时间步的关键交叉口；记录目标交叉口在各时间步上的重要程度变化轨迹，可揭示其重要性时序特性。

表1 实例路网统计特征值Table 1 Characteristics of example road network

3.1 交叉口重要性排名统计特征

统计147 个节点在全天96 个时间步的重要性排名变化，绘制箱线图如图2 所示。排名数值越小，说明交叉口在对应时间步重要性越高。

图2 显示，各交叉口重要性排名波动较大，证明了在繁忙的路网中，交叉口的重要性不宜用一组固定排序描述，这体现了分时段考察关键交叉口的必要性。图2 中（i）框选部分包括了重要性一度排名首位的路段，其排序统计中位数明显小于均值，说明其重要性分布为偏态分布，个别时间步中其排序靠后影响了总体均值；而（ii）框选部分所包括的路段规律相反，多数时间步中其排序靠后，偶见排序靠前的时间步导致其排序均值小于中位数。而且，交叉口重要性排序的中位数集合，其阈值比均值集合更广。可见，采用中位数作为代表指标衡量一段时间内交叉口重要性水平，其抗干扰能力和区分度都更具优势。

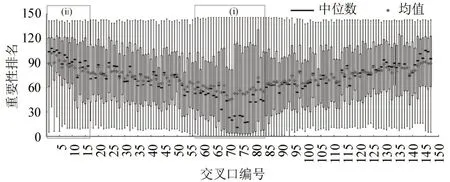
图2 全天各交叉口重要性排名箱线图Fig.2 Boxplots of importance-ranking for all intersections all-day

3.2 交叉口重要性排名时序特性

图3 包括3 个随机交叉口（编号16、92、145）的重要性排名时序信息。可见，虽各序列波动程度不同，但均呈时段性聚集态势，即交叉口重要性水平在若干连续时间步上有一定持续性。据此，可对各交叉口排名序列聚类分析，一方面可减少数据点数量，提升模型对长时段分析的适应性；另一方面，聚类可消除短时间内排名微小波动以及偶发异常值的干扰，有利于清晰展示交叉口重要性排名的时序特性与整体变化趋势。

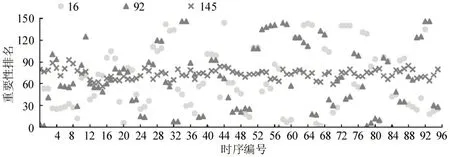
图3 随机交叉口的重要性排名时序散点图Fig.3 Scatter diagrams of importance-ranking for stochastic intersections

本文采用Luo 等[16]提出的改进快速查找密度峰值算法实现交叉口重要性排名序列聚类，该方法基于模糊理论，可有效识别时间序列中不同水平的连续点簇，并避免离群值的影响，鲁棒性较好。图4为6 个典型交叉口重要性聚类结果，相对于散点图，其以较少数据点体现了交叉口重要性的波动情况。分图题中排序为各样本全日重要性排名中位数（下同）。

图4显示，一天内各交叉口重要性排名均存在波动。重要性中位数排名首位的72 号交叉口，并非全天都是最重要的交叉口；排名末位的1号交叉口，其重要性排名一度进入前50%。这说明，对于密度较大、承载交通联系任务较重的局部路网，相对于用单一统计值筛选关键交叉口，动态化观测更具合理性。此外，各交叉口重要性排名并非完全无规律的频繁波动，而是普遍存在平台期，这说明，路网中的交叉口分阶段地体现出其功能关键性，应在不同交通需求场景下进行分时段分级管理。

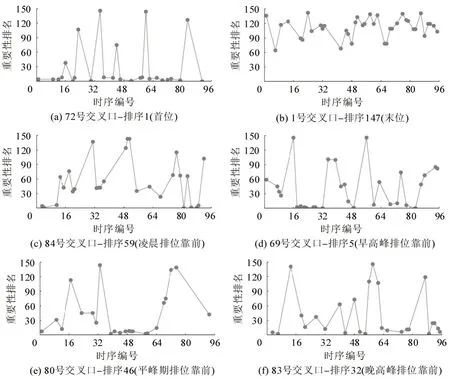
图4 典型交叉口重要性排名聚类结果Fig.4 Importance-ranking clusters of typical intersections

3.3 路网重要交叉口分布特性

图5 为不同时间步或统计口径下全路网重要性排序靠前的交叉口分布示意图。不难看出，FSAM 模型在不同时段识别出的重要交叉口集合存在差别，尽管有少数交叉口同时在多个时段被认为有较强重要性，但总体而言，在不同场景下管理交叉口时应各有侧重。

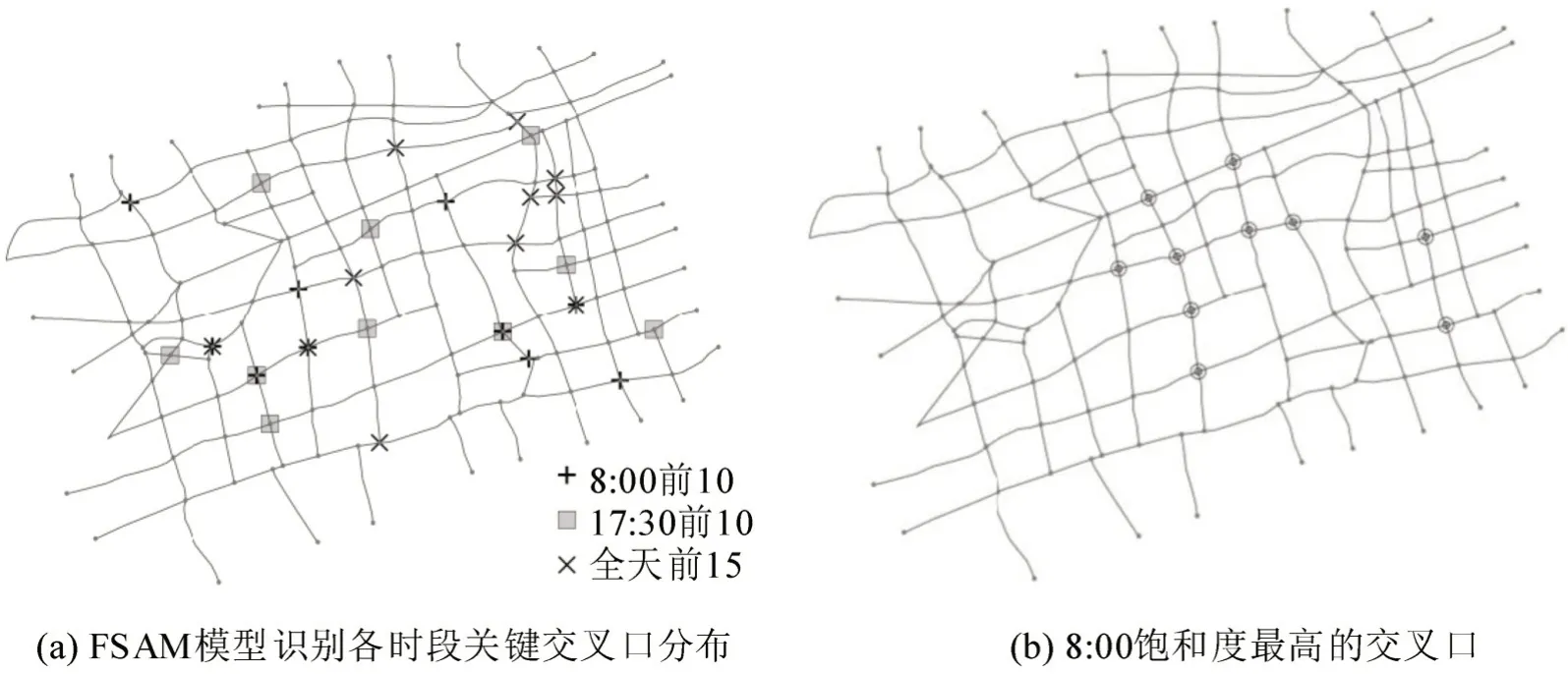
图5 关键交叉口位置分布Fig.5 Locations of critical intersections on different times of day

8:00 时间步上用FSAM 模型和饱和度指标分别识别的关键交叉口集合存在较大差别，前者广泛分布在路网上，而后者常集中于某条路段上。原因在于饱和度仅代表了一个时间步中交叉口剩余服务能力的大小，而FSAM模型在空间上考量了目标交叉口与相邻交叉口的关联强度，在时间上考量了目标交叉口对周边交通影响力的持续性，有更丰富的内涵。

3.4 模型时间颗粒度敏感性分析

为考察FSAM模型输出结果的稳定性，对其进行时间颗粒度敏感性分析。分别按照15，30，60 min时间颗粒度集聚计算各时段速度均值，并重复FSAM建模求解过程，得到各交叉口在3种时间颗粒度下的重要性排名时序变化，部分示例如图6 所示。由图6 可知，不同颗粒度模型对交叉口重要性的排名序列趋势基本相似。随着颗粒度越大，持续时间较短的波动被平滑，部分细节信息丢失，呈现出整体波动越小。为量化3组FSAM模型对同一时间步上交叉口重要性排序的一致性，取早高峰代表时间步7:00 和8:00 及晚高峰代表时间步17:00 和18:00。对每个时间步，分别两两比较3 个颗粒度模型产生的排序数列（均包含147个元素）。

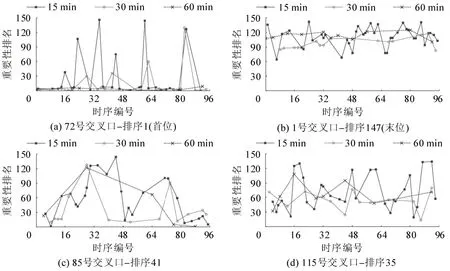
图6 不同颗粒度下交叉口重要性排名变化趋势（按15 min颗粒度为时序编号）Fig.6 Importance-ranking trends of example intersections with various time granularities（interval indexed by 15 min）

本文选择肯德尔系数（Kendall'sτ）作为一致性指标，该系数常用于同维度排序数列的相关性比较，在[-1,1]区间取值，结果越接近1，说明排序结果越趋一致。以其评价上述数列关系，结果如表2所示。综合来看，3个模型一致性较好，但在重要性频繁波动的早高峰期间，15 min和60 min颗粒度的结果一致性有所削弱。

表2 不同颗粒度模型对交叉口重要性排序一致性评价Table 2 Consistency of importance-ranking by modelswith various time granularities

综合敏感性分析结果，在计算能力满足要求的条件下，建议按照15 min 评价交叉口重要性，以保证更多波动信息；如对计算速度有要求，较粗颗粒度的模型可在一定程度上保证重要性趋势的呈现。

4 结论

本文将城市路网视为时序网络，提出FSAM模型识别路网中的关键交叉口。实例研究表明，密集路网交叉口重要性排序普遍存在较大波动性，以其中位数作为时段内重要性水平的评价指标更具合理性；FSAM模型计算得到的交叉口重要性排名有阶段持续特征，体现出分时段评价关键交叉口的必要性；相对于依赖饱和度等单一指标识别交叉口，FSAM模型的内涵更加丰富，被认定为重要性较高的交叉口在空间上也更加趋于分散；不同时间颗粒度下的FSAM 模型对同一交叉口重要性排序的趋势一致性较好，但粗颗粒度模型丢失了部分波动信息，应结合实际需求选取颗粒度。FSAM模型符合路网作为时序网络的特性，具有较好的解释性和稳定性，输出结果为定量指标，可作为制定城市交通重点管理策略的依据。