多模式疏散交通车队配置与车道分配协同优化研究

刘家林，贾斌*,2，刘正，姜锐，李新刚

（1.北京交通大学，交通运输学院，北京 100044；2.西安工业大学，经济管理学院，西安 710021；3.郑州航空工业管理学院，管理工程学院，郑州 450046）

0 引言

近年来，全球各类自然灾害、事故灾难、公共卫生事件和社会安全事件频繁发生，造成了巨大的经济损失和人员伤亡。据统计，我国2020年各种自然灾害造成1.38 亿人次受灾，紧急转移安置589.1万人次，直接经济损失3701.5亿元[1]。利用道路交通疏散受灾人员是应对各种有预警灾害事件（洪水、飓风、山火及危险品泄漏等）的有效方法，能够最大限度地减少人员伤亡与财产损失。

就疏散交通方式而言，发达国家由于小汽车保有量高和人员居住分散等原因，早期的疏散研究和疏散组织多以小汽车疏散为主。然而，2005年美国新奥尔良的“卡特里娜”飓风造成1800 多人伤亡，其中，71%的遇难者年龄超过60 岁，47%的遇难者年龄超过75岁，可见，疏散老年人等无车群体对降低灾害损失至关重要[2]。此后，发达国家开始重视多模式疏散交通研究和规划，涵盖疏散集结点选址，疏散路径和时刻表规划及多模式疏散网络设计等[3]。对我国而言，人口老龄化日益严重，人均机动车保有量和道路密度均低于发达国家，人群高度聚集的大型活动较多，发展多模式交通协同疏散更符合我国现阶段国情[4]。

多模式交通疏散的研究起步较晚，研究方法主要有：模拟仿真、网络流模型和交通分配理论。金美莲等[5]构建了具有统一尺寸元胞的元胞自动机模型，研究不同的步行、自行车和机动车混合比例对疏散时间的影响，结果表明：在一定混合比例下，多模式交通疏散可以提高疏散效率。为了克服仿真模型计算量大和普适性差的问题，多模式交通疏散问题常被建模为多商品网络流模型，薛白等[6]考虑受灾人员和物资网络加载的差异性，构建了最小费用流模型，并提出一种基于时间扩展的最小费用路线算法求解模型。段晓红等[7]为了提高救援交通的可靠性，建立救援与疏散协同优化的双层规划模型，并设计一种双层蝙蝠算法求解模型。ABDELGAWAD 等[8]提出涵盖小汽车、公交车和地铁的多模式交通疏散规划框架，协同优化车辆调度、路径选择和目的地选择。WANG等[9]建立了多模式车队和道路逆流联合优化的双层模型，结合基于优先级的最小费用流算法和禁忌搜索算法求解模型。相比单模式疏散，上述网络流模型建模求解更加复杂，没有考虑疏散交通的动态性，无法捕获疏散交通流的动态传播以及交通拥堵等现象。然而，由于供需矛盾突出，大规模疏散中极易发生交通拥堵，从而降低疏散效率或造成二次伤害。近年来，基于动态交通分配方法建模多模式疏散问题成为研究热点，YANG等[10]提出了多模式动态系统最优疏散模型，用双排队模型加载公交车流，以便捕获拥堵排队，基于连续平均法的序列优化算法求解模型。LIU等[11]提出了疏散车辆和救援车辆协同的两阶段优化模型，采用路段传输模型动态加载交通，研究不同的救援入口开放方案对救援和疏散的影响。上述研究中，需求端的车队规模是输入参数，没有考虑车队配置和车道分配的联合优化，疏散效率有望进一步提高。此外，以疏散时间最短为优化目标，忽视灾害的风险性，导致车辆为了节省旅行时间，可能多次穿越高风险区域，危害疏散人员的生命安全，与实际情况不符。

综上所述，本文在考虑疏散交通动态性和风险性的基础上，从平衡疏散系统供需矛盾的角度出发，将基于元胞传输模型的系统最优动态交通分配框架（CTM-based SO DTA）[12]拓展到多模式交通动态疏散问题，以最小化疏散总风险为目标函数，构建多模式交通协同的动态疏散优化模型，以实现疏散需求、车队规模、路网能力以及疏散交通流量的协调优化，降低疏散总风险，提高疏散效率。

1 问题描述

交通疏散的首要目标是尽快将受灾人员转移到避难所，避免引发交通拥堵。考虑一个多源多汇的多模式交通疏散网络G（N,A），其中，N为交叉口，A为路段。为了刻画交通流量演化的动态性和捕获交通拥堵产生与消散，采用元胞传输模型（CTM）加载疏散交通流，疏散网络G（N,A）被离散为元胞网络G（C,E），其中，C为元胞集合，E为元胞链接集合。

路段离散为多尺寸元胞如图1 所示。在单模式交通网络中，元胞尺寸相同，其长度等于车辆自由流速度乘以仿真时间步长，该规则确保了模型的稳定性，使得任意时间步元胞上承载的车辆数守恒，如图1（b）和图1（c）所示。在多模式交通网络中，疏散车辆的自由流速度和有效长度（包含最小安全间距）不同，进而导致元胞的尺寸、阻塞密度和通行能力参数不同。因此，根据多模式车辆的自由流速度，将路段离散为多尺寸元胞，如图1（d）所示。每种类型的车辆只能在自己的元胞网络中行驶，有效避免了统一尺寸的元胞划分导致CTM模型不稳定或车辆无法及时清空的问题，提升网络清空时间估计准确度。

图1 路段离散为多尺寸元胞示意图Fig.1 Schematic diagram of discretization of road segments into multi-size cells

以小汽车和公交车参与疏散时，小汽车的自由流速度是公交车的2倍为例，多模式交叉口元胞的分流合流情况如图2所示。

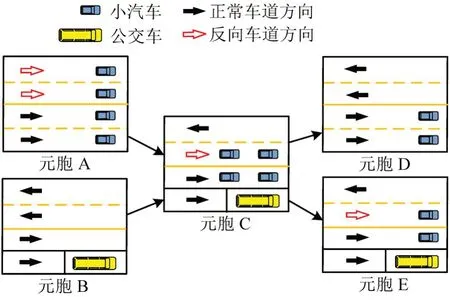
图2 多模式交通交叉口元胞的合流分流示意Fig.2 Merging and diverging intersections of multimodal vehicles

上游元胞A中4辆小汽车占用4条车道，其中，2条车道是反向车道；元胞B中1条车道被1辆公交车占用；元胞A 和B 车辆合流进入下游的元胞C，小汽车占用2 条车道，其中，1 条为反向车道，公交车占用1条车道，1条车道未被使用；元胞C分流到下游的元胞D和元胞E，元胞D中2车道被占用，元胞E 中3 条车道被占用，包含1 条被小汽车占用的反向车道。

相比单模式交通疏散只优化车道管理方案和疏散交通流量。在组织多模式交通疏散时，管理者需要同时决策车队配置方案、车道分配方案以及疏散交通流量，更好地平衡疏散需求与道路供给，进一步提高疏散效率，降低疏散总风险。

2 模型建立

2.1 基本假设

基于《国家突发公共事件总体应急预案》[13]提出以下基本假设：

（1）疏散人员听从管理者的统一指挥，疏散开始前，道路网络上无疏散车辆运行，应急避难场所位置已知。

（2）灾害周围区域被划分为高、中、低风险区，采用相对风险值衡量危险程度。

（3）受到固定的道路设施（中央分隔带和护栏等）限制，难以频繁改变车道管理方案，将车道变量描述为静态的整数变量，且同一路段的车道分配方案相同。

2.2 符号说明

设元胞集合为C，包含风险源元胞集合CR，避难所元胞集合CS，普通中转元胞集合CO，元胞索引为k,i,j；Γ-（i）为当前元胞i的上游元胞k的集合，即k∈Γ-（i）；Γ（i）为元胞i的下游元胞j的集合，即j∈Γ（i）；设E（i）与元胞i同属一个路段的元胞集合；设元胞i的总车道数为Zi，包括对向车道数。

设车辆类型的集合为M，索引为m，其中，m类型车辆的有效长度（包含最小安全距离）为lm，最大载客量为pm，自由流速度vm，拥堵波传播速度wm。

设时间步集合为Ψ={0,1,…,T}，索引为t，时间步长度为τ。其他参数包括：t时刻，m类型车辆在元胞i的通行能力为；t时刻，元胞i最多承载的m类型车辆数为；风险源元胞i中的疏散人数为Di（i∈CR）；t时刻，元胞i的相对风险水平为。

设离散变量di,m（i∈CR）为风险源元胞i内m类型车辆的数量，即多模式车队的规模；设连续变量为t时刻元胞i内m类型车辆的数量；连续变量为t时刻从元胞i到元胞j的m类型车辆的数量；设整数变量zi,m为元胞i内m类型车辆占用的车道数量。

2.3 目标函数

在大规模交通疏散优化问题中，通常基于Wardrop 系统最优准则分配疏散交通流量，优化目标一般为最小化所有人的总旅行时间或最小化网络清空时间。但是，最小化时间成本的目标函数忽略了路网风险和灾害扩散等因素，导致车辆尽量选择最短路出行，无法通过绕行避开高风险区域，威胁疏散人员的生命安全。

此外，将分段线性的CTM 松弛为不等式约束产生了“车辆滞留”现象，表现为下游路段有足够空间，但一些车辆仍然滞留在当前路段而没有驶入下游路段[14]。在疏散中，应该避免车辆滞留在高风险区域，减少疏散人员的暴露风险和死亡威胁。鉴于此，本文提出最小化疏散总风险的目标函数为

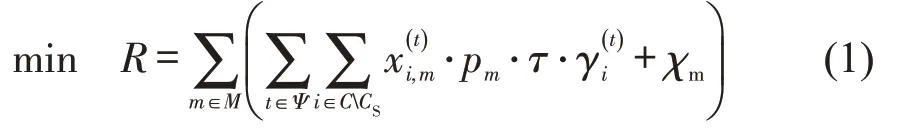
式中：R为从时间和空间维度刻画的疏散总风险，疏散人员越快离开较高风险区域，则疏散总风险越小；为乘坐m类车辆的疏散人员的总旅行时间；为乘坐m类车辆的疏散人员承担的暴露风险；连续变量χm为消除“车辆滞留”现象而添加的惩罚项。

2.4 约束条件

为了平衡疏散系统的需求与供给，引入车队配置约束和车道分配约束；为了模拟疏散交通在路网上的动态运行过程，捕获疏散交通流状态动态变化，引入流量动态加载约束和消除“车辆滞留”的约束。

2.4.1 车队配置约束

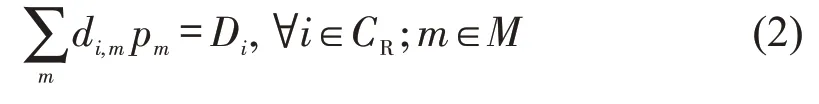
式（2）为风险源i的总需求守恒约束，确保所有人都被疏散；式（3）为配置车辆的非负约束，可以采用单模式或多模式，具体车辆数由优化确定。

2.4.2 流量动态加载约束

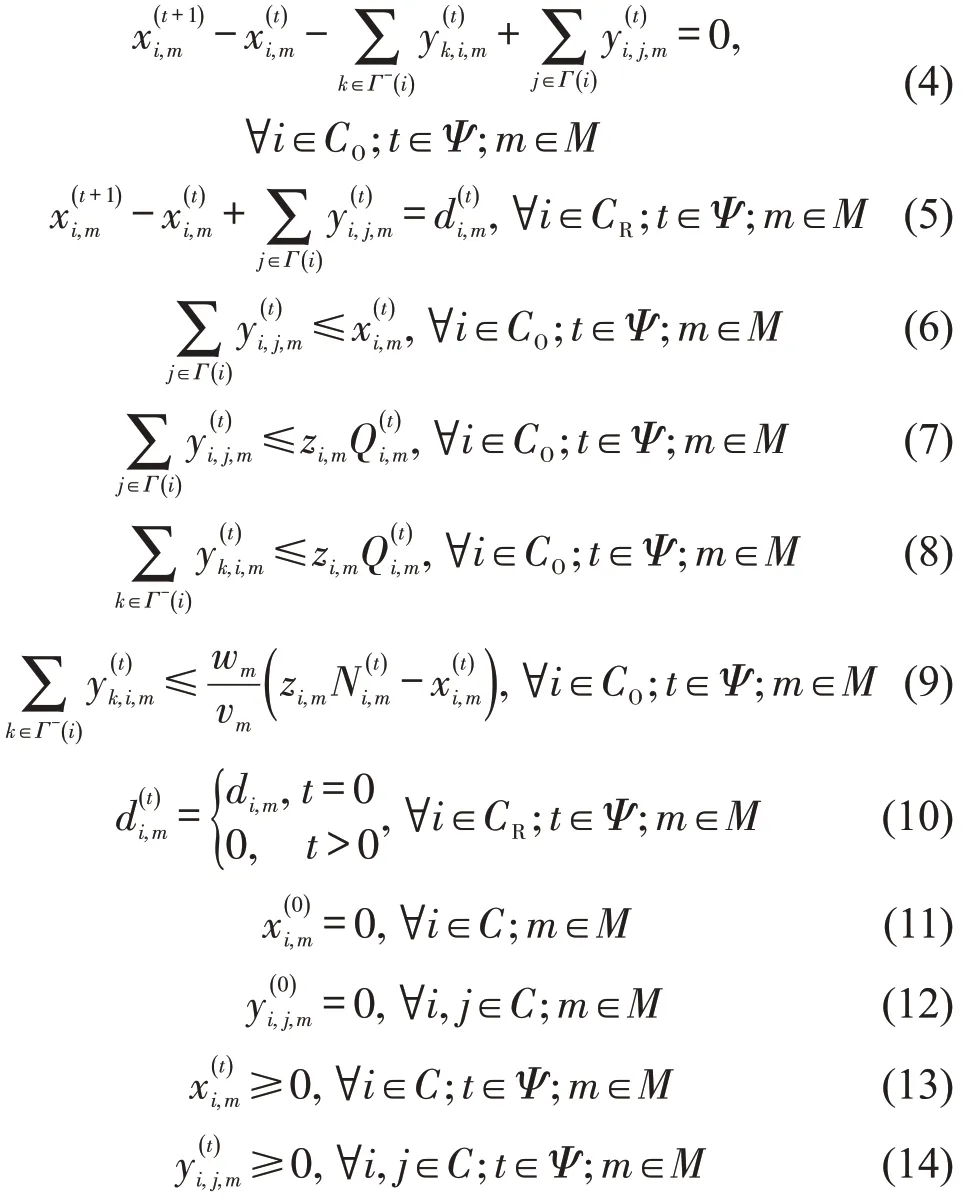
式（4）为路段上承载的各类车辆数守恒约束；式（5）为疏散车辆离开危险源元胞，进入疏散网络；式（6）～式（9）为松弛的元胞传输模型约束，其中，式（6）和式（7）为元胞的发送函数，即当前元胞的流出量不超过该元胞承载的车辆数和最大通行能力；式（8）和式（9）为元胞的接受函数，即当前元胞的流入量不超过其最大通行能力和剩余空间；式（10）为所有车辆在疏散开始时刻加载到路网上；式（11）和式（12）为初始时刻网络被完全清空；式（13）和式（14）为元胞的车辆数和流入、流出量的非负约束。

2.4.3 车道分配约束

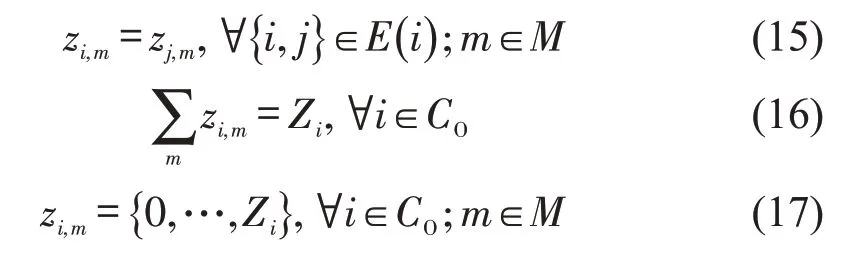
式（15）描述了隶属同一路段的多个元胞的车道分配方案相同；式（16）为元胞内总车道数目的约束；式（17）为车道的整数取值范围约束。

2.4.4 消除“车辆滞留”约束

元胞传输模型被松弛成不等式约束式（5）～式（8），导致可行解不一定满足原来的分段线性等式形式，当该组约束全取小于号时会产生不合理的“车辆滞留”现象。本文采用添加惩罚项的方法抑制不合理的流量模式发生[14]，使得车辆尽快离开高危险路段。

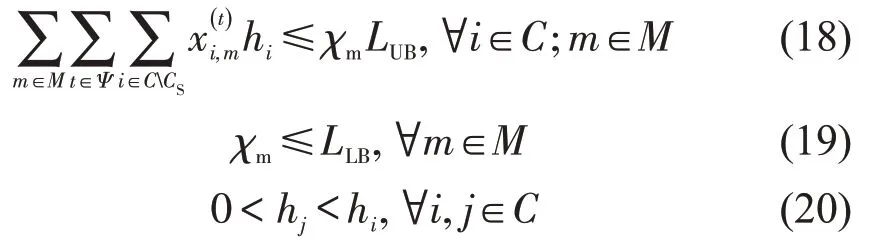
式中：hi为惩罚因子；χm为抑制“车辆滞留”的虚拟变量，该变量的上、下界分别为LUB、LLB，本文分别取1000000 和1。式（18）和式（19）为流量滞留的惩罚约束；式（20）为下游元胞惩罚因子hj小于当前元胞hi，即惩罚因子取正数且在疏散方向上单调递减，迫使车辆向下游移动。

3 案例分析

3.1 场景描述

采用Nguyen-Dupuis 路网进行算例分析，如图3所示。

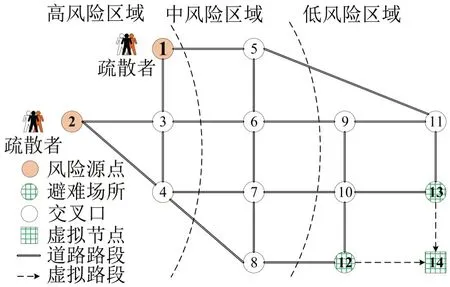
图3 Nguyen-Dupuis疏散交通网络Fig.3 Nguyen-Dupuis evacuation network

该网络有13 个节点、19 个路段和4 个OD 对，每条路段均为双向4车道，路段长度和最大通行能力如表1所示。

表1 疏散网络参数Table 1 Evacuation network parameters

假设风险源为节点1 和节点2，受影响的居民在两个节点集合等待疏散，避难所位于节点12 和节点13。为了易于模型求解，将避难所节点连接到1 个虚拟的超级避难所（节点14），多源多汇网络被转化为多源单汇网络。假设路网风险水平从风险源到避难所单调递减，参考《危险化学品重大风险源监督管理暂行规定》（GB18218）提出的风险区域划分方法[15]，将疏散路网划分为高、中、低风险区域，相对风险值在疏散期间固定，取值分别为5、3 和1。假设小汽车和公交车参与疏散，车辆的性能参数如表2所示。

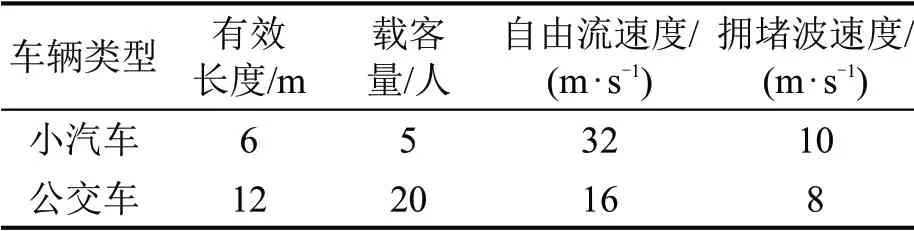
表2 两类车辆的性能参数Table 2 Performance parameters of two-class vehicles

应用元胞传输模型模拟疏散交通流动态加载过程时，设置仿真时间间隔为10 s，总时间步为100（大约28 min），根据自由流速度将道路网络离散为多尺寸元胞网络。其中，小汽车元胞长度为320 m，路网包含48 个元胞和61 条链接；公交车元胞长度为160 m，路网包含93个元胞和113条链接。

在小汽车元胞网络中，最大通行能力为每个时间步48 辆，最大容量为每个元胞216辆。在公交车元胞网络中，最大通行能力为每个时间步16 辆，最大容量为每个元胞52 辆；虚拟元胞和链接的容量和通行能力取10000。

为了验证所构建的多模式协同疏散模型在平衡疏散需求和道路供给方面的效果，本文将疏散总需求在4000～80000 人的取值范围内进行变化，设置了20 组对比试验。每组实验中，总需求被平均分配给风险源1 和风险源2，分析不同疏散需求下疏散系统的性能、供需关系以及疏散路径。

3.2 结果分析

本文提出的模型为混合整数线性规划（MILP），可以利用商业求解器快速解决，满足疏散时效性的要求。本文在MATLAB 2018 平台上调用GUROBI 9.2求解模型。

3.2.1 供需关系分析

就车队需求而言，在不同的疏散人数下，两个风险源的最优车队配置方案如图4 所示，r为整个车队中公交车的配置比例。车队总规模和路网利用率随着疏散需求增加而变化的趋势如图5所示。

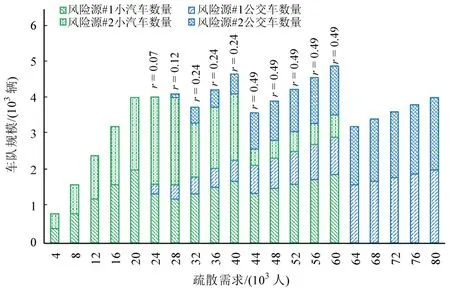
图4 不同疏散需求下两个风险源的最优车队配置Fig.4 Optimal fleet configuration of two risk sources under different evacuation demand

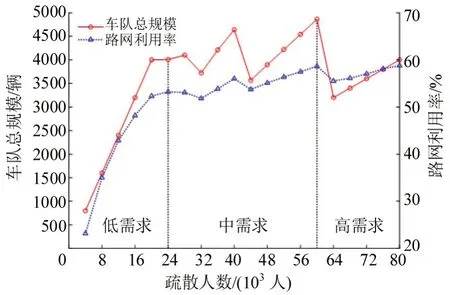
图5 不同疏散需求下的车队规模与路网利用率Fig.5 Fleet size and road network utilization under different evacuation demand

本文将不同的最优车队配置策略（全是小汽车，多模式车队，全是公交车）对应的疏散需求定义为低、中、高疏散需求3 个区间。当处于低疏散需求时（24000人以下），路网能力充足，高风险区域排队车辆少，采用速度较快的小汽车是最优疏散策略。当处于高疏散需求时（60000 人以上），大容量的公交车更有优势，因为，使用公交车可以降低车队总规模，进而减少在风险源排队的人数。存在中等疏散需求区间（24000～60000 人），组织多模式车队疏散比使用单模式车队更优。整个疏散车队的公交比例呈阶梯式增加，最优公交配置比例为[0.00,0.07,0.12,0.24,0.49,1.00]，当疏散需求超过中等疏散需求区间的上界，公交比例会急速增加到1.00，即全用公交车疏散，这种现象是由于车道的离散化分配造成的。因此，在组织多模式车队疏散时，存在公交车配置比例的上限，本案例中为0.49。

为了衡量疏散期间道路网络供给，设计“路网利用率”指标量化时空维度上整个网络的负荷程度，m类车辆路网利用率的计算式为

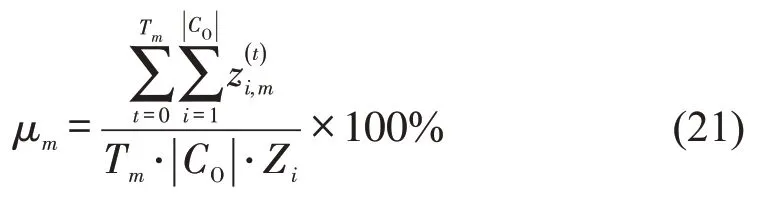
式中：为m类车辆在t时刻占用元胞i的车辆数；|CO|为路网元胞的数量（不包含虚拟节点）；为清空时间内被占用的车道数之和；Tm· |CO|·Zi为清空时间内可利用的车道数的总和。

车队规模与路网利用率的变化趋势相同，说明多模式协同疏散模型实现了疏散需求、车队规模和车道分配方案的协调优化，有效提升了网络利用率，降低了疏散总风险。路网利用率曲线呈上凸式增长，先快后慢，最后，趋于稳定。在低疏散需求区间，路网通行能力充足，随着疏散需求增加，车队规模增大，使用的道路资源增多。在中疏散和高疏散需求区间，路网通行能力不足，一旦所有的可行路径被车辆占用，为了避免路网上的交通拥堵，再增加的车辆只能在灾害点排队等待，路网利用率将趋近稳定。因此，在疏散网络中，由于道路之间通行能力的限制，并非所有的路段疏散能力都能被车辆完全使用，存在路网利用率的上限，本文中该值约为60%。

图5 的中需求区间表明，在组织多模式车队时，车队总规模和路网利用率随着疏散需求单调增加呈现凹凸波动。因为受疏散车辆离开受灾区域的道路通行能力限制，公交车只存在有限种路径选择方案，每种方案占用的车道数量呈非线性变化，造成车队总规模呈现非线性变化。不同疏散需求下公交车占用的车道数量如图6所示。

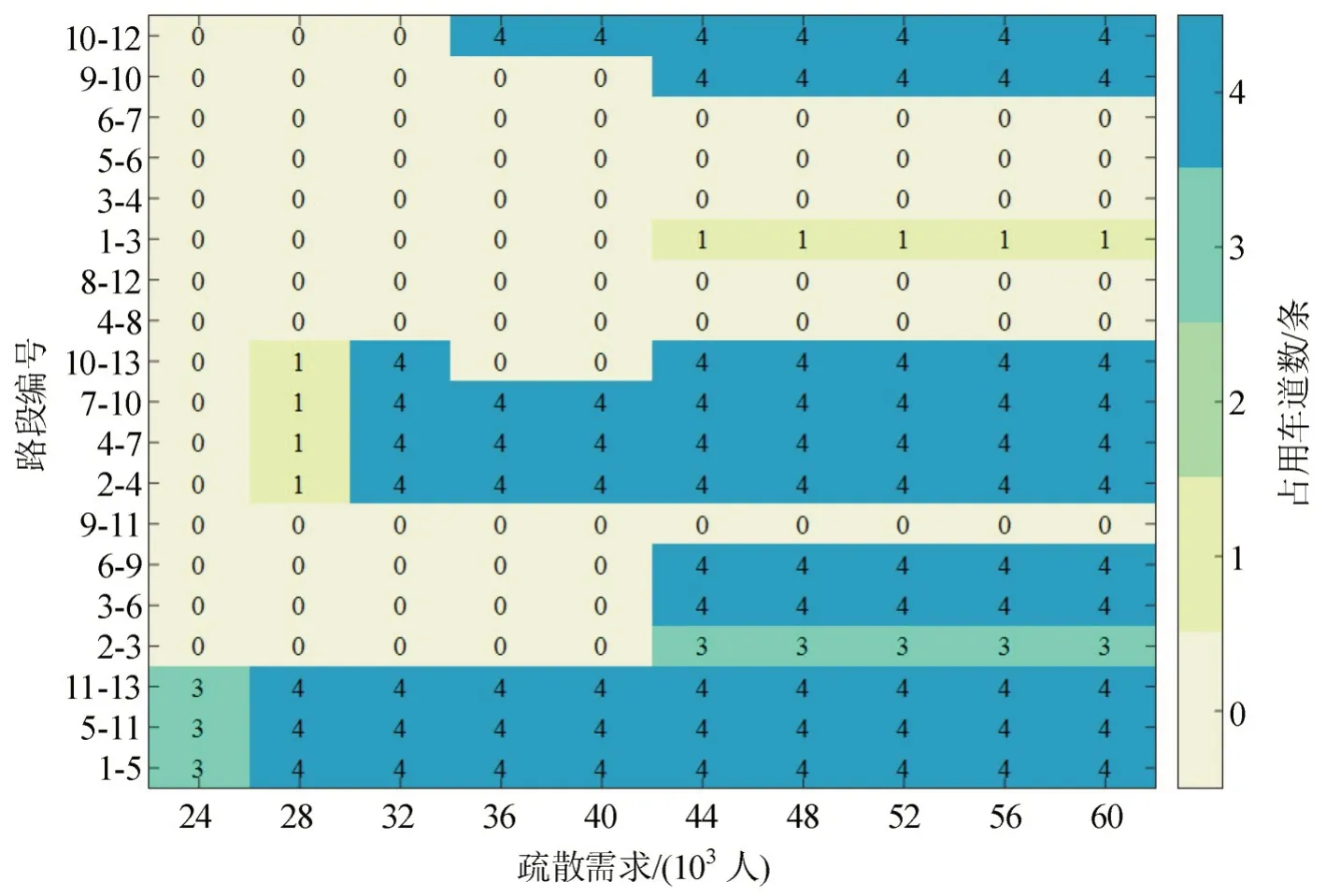
图6 中等疏散需求下公交车占用车道数量Fig.6 Number of lanes occupied by buses under medium evacuation demand

由图6可知，公交车占用的车道总数呈阶梯式变化，分别为9，16，28 和48，对应的最优的公交比例为0.07，0.12，0.24 和0.49。具体地，当需求为24000 时，仅有风险点#1 配置了公交车，公交车疏散路径为1-5-11-13，使用9个车道；当需求为28000时，公交车疏散路径为1-5-11-13和2-4-7-10-13，使用16 个车道；当需求为32000 时，公交车疏散路径为1-5-11-13和2-4-7-10-13，使用28个车道；当疏散需求在[44000，60000]区间，公交车疏散路径为1-5-11-13、2-4-7-10-13、1-3-6-9-10-13 和2-3-6-9-10-12，使用48个车道，随着疏散需求继续增加，没有新的疏散路径可用，新产生的车辆只能排队，车队总规模和路网利用率呈线性增加。

3.2.2 疏散性能分析

交通疏散旨在通过优化现有交通系统，以期最大限度地减少受灾人员的暴露风险和死亡威胁。在特定的疏散问题中，评价疏散系统性能的指标取决于灾害性质、强度以及其他环境因素[15]。

本文基于疏散总风险和网络清空时间两个指标，分析不同疏散需求对疏散风险和效率的影响。其中，疏散总风险函数式（1）基于元胞的相对风险水平和疏散总旅行时间构建，用于评估疏散人员的暴露风险程度。网络清空时间（ENCT）定义为最后一辆车离开网络的时间，包括排队时间和旅行时间两部分，通常用来评估疏散效率。在多模式交通网络中，首先，基于流量分配结果获得m类型车辆的网络清空时间Tm；然后，确定整个疏散系统的网络清空时间TENCT为

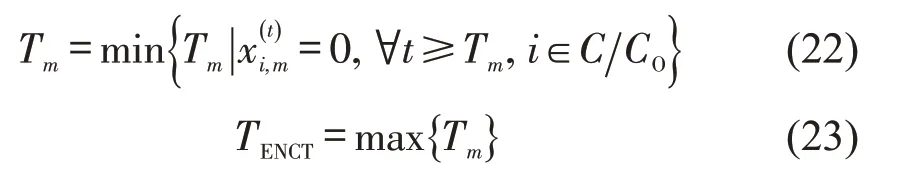
不同疏散需求下的疏散总风险值如图7所示。

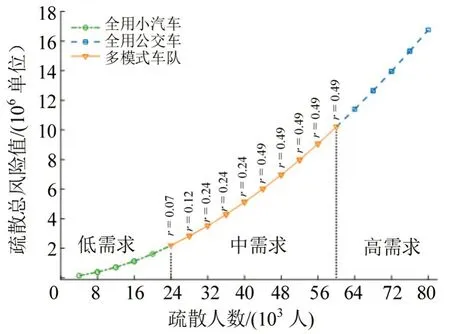
图7 不同疏散需求下的疏散总风险Fig.7 Total evacuation risk values under different evacuation demand

随着疏散需求线性递增，疏散人员承担的总风险呈上凹式增长，增长率逐渐增大。因为，当疏散需求小于路网通行能力时，车辆可以从高风险区域快速移动到低风险区域，没有车辆滞留在风险源，疏散总风险增长较慢。当疏散需求超过路网通行能力时，大量的疏散人员滞留在灾害点等待疏散，导致系统总风险随着疏散人数增多呈指数增加。因此，在应对灾害事件时，确定合理的疏散范围和疏散人数十分重要，其直接影响疏散人员的暴露风险。不同疏散需求下的网络清空时间值如图8所示。

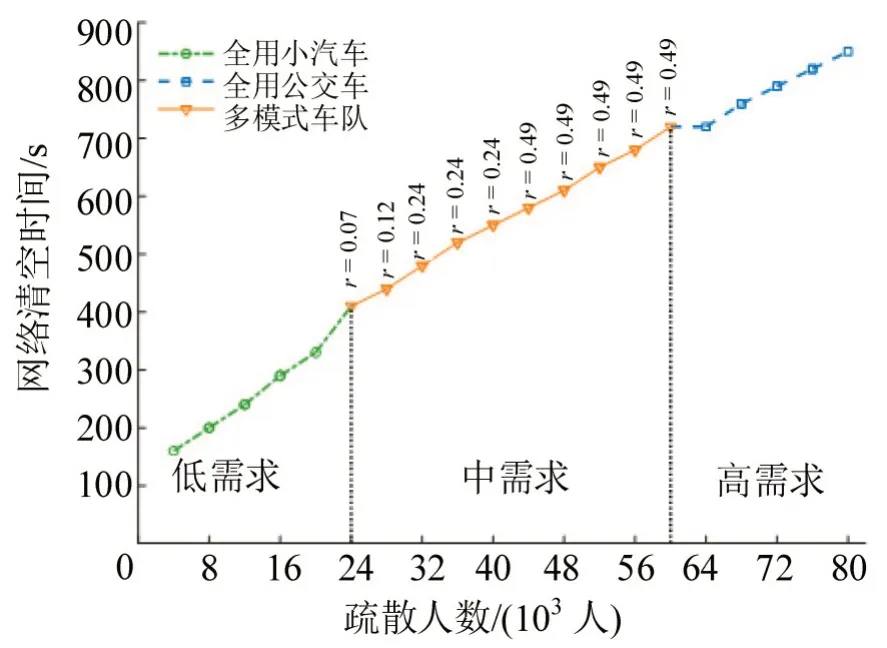
图8 不同疏散需求下的网络清空时间Fig.8 Network clearance time under different evacuation demand

与疏散总风险随着疏散需求增加呈指数增长不同，网络清空时间随着疏散需求增加呈分段线性增加。因为，网络清空时间主要由疏散网络出口路段的通行能力决定，而疏散总风险考虑了整个网络的流量演化情况，因此，疏散总风险指标对疏散需求的变化更加敏感。忽略灾害对疏散路网风险性的影响时，仅以最小化网络清空时间作为疏散目标，可能高估了疏散效率。鉴于此，对毒气泄漏和火灾等高扩散性的灾害，不能只考虑最短的网络清空时间，需要关注路网的风险水平和疏散人员的暴露风险；而对泥石流和建筑物倒塌等低扩散性的灾害，可采用网络清空时间制定疏散预案。

以中需求区间为例，进一步对比分析3种不同疏散交通方式下（全用小汽车、全用公交车、组织混合车队）的疏散总风险值R和网络清空时间TENCT，结果如表3所示。

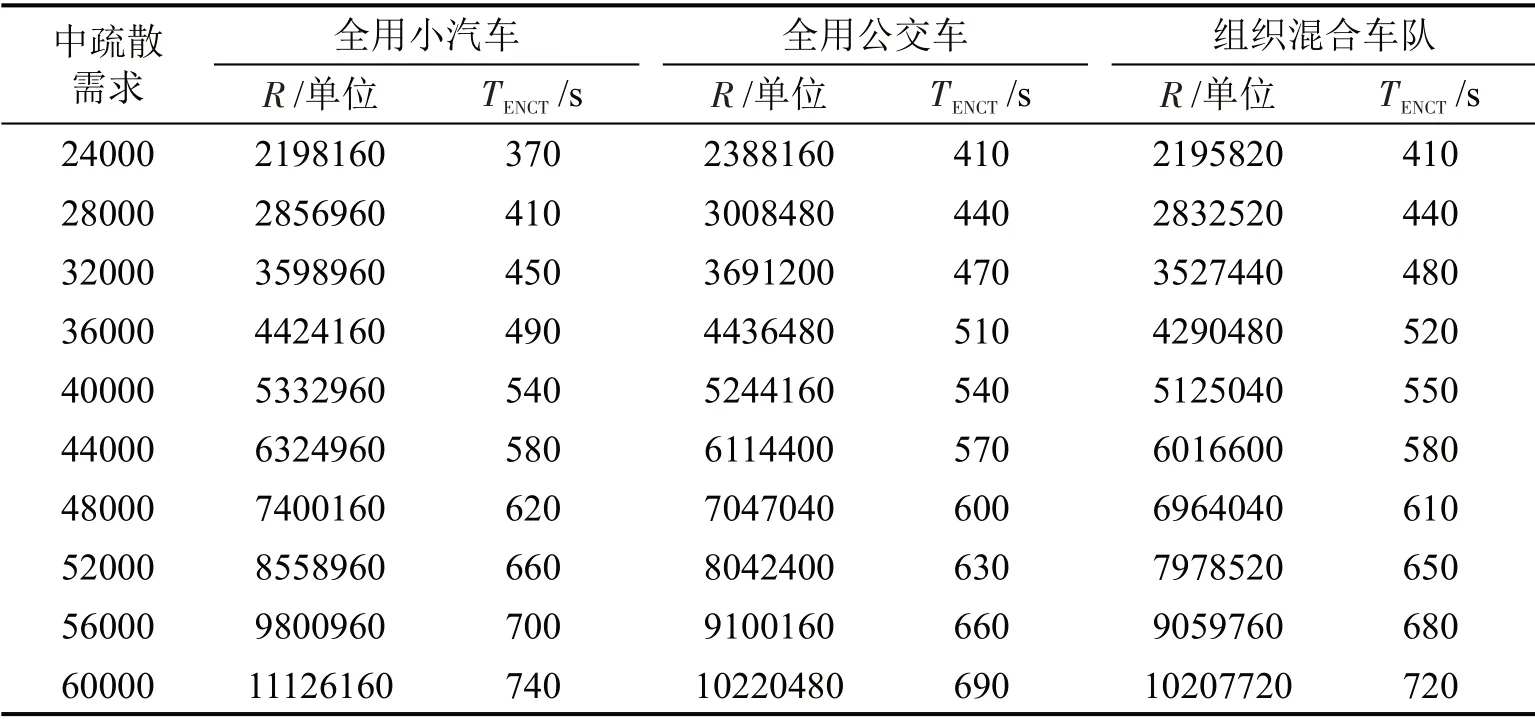
表3 中疏散需求区间3种策略对比Table 3 Comparison of three strategies under medium evacuation demand

组织多模式车队虽然增加了部分车辆的网络清空时间，但使得系统的疏散总风险降低，与全用小汽车或公交车疏散相比，系统总风险值降幅最高达9%。表明，在危险品泄漏和火灾等具有扩散性的灾害救援中，可以使部分车辆暂时停留在低风险区域，使高风险区域滞留的车辆优先驶出，以降低疏散人员的总风险。

3.2.3 疏散路径分析

选取4个疏散需求点，分别为低需求20000人，中需求40000 人和60000 人，高需求80000 人，比较分析疏散路径和车道分配方案，如图9 所示，图中数字为占用车道的数量，包含反向车道。

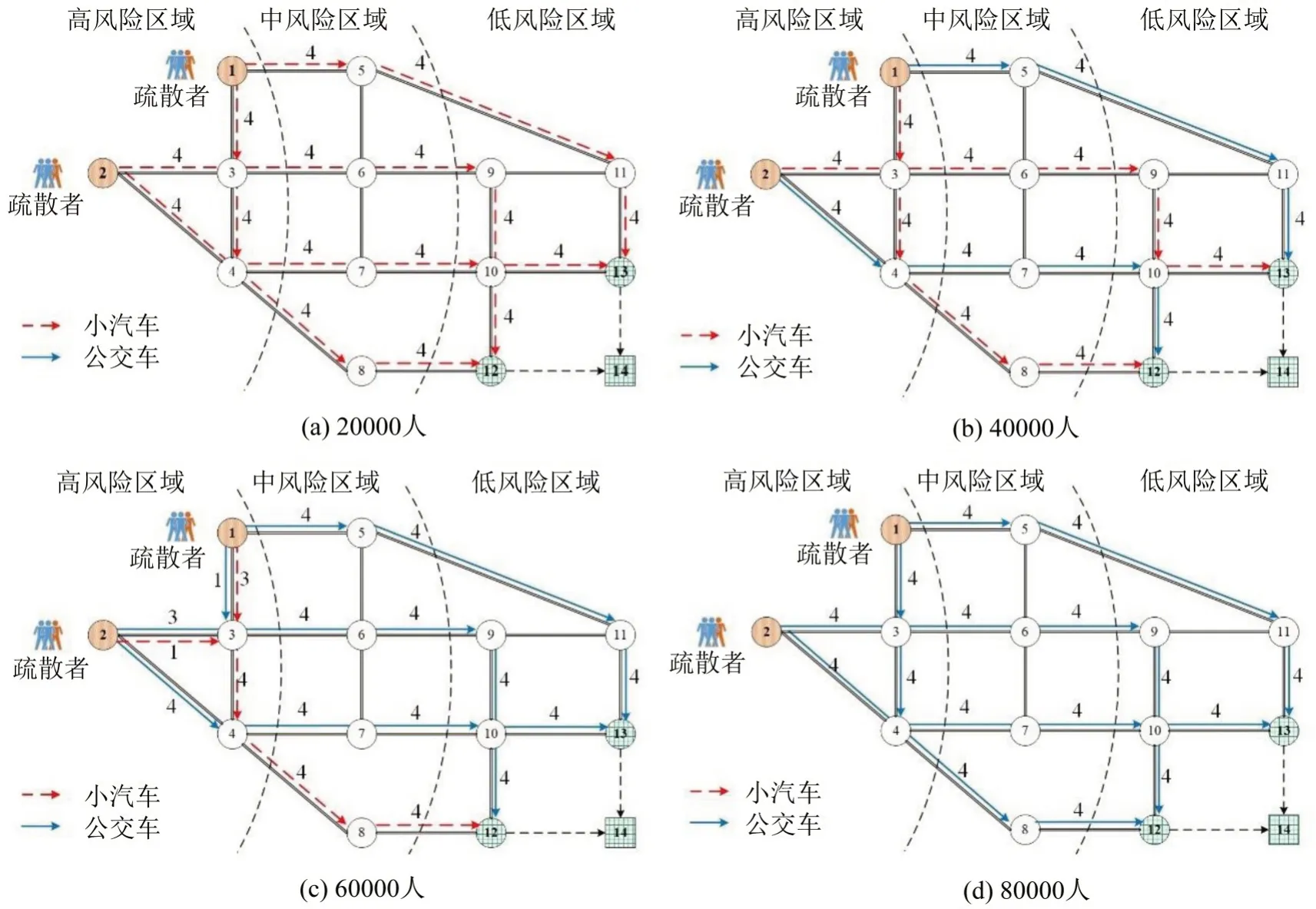
图9 不同疏散需求下疏散路径及车道分配方案Fig.9 Evacuation routes and lane allocation schemes under different evacuation demand

4 种疏散需求下，车辆会优先使用最短路尽快驶出高中风险区域，如路径1-5-11-13，2-4-8-12。绕行主要发生在低风险区域，例如，车辆选择路径2-3-6-9-10-13 绕行，而不使用路段9-11，避免因共享路段11-13 导致最短路径1-5-11-13 的通行能力降低，使车辆拥堵在中高风险区域，增加疏散总风险。

低疏散需求时，全部采用小汽车疏散，高疏散需求区间，全部采用公交车疏散，但两者疏散路径相同，如图9（a）和图9（d）所示。而且2条反向车道，以便尽快驶出高中风险区域。

中疏散需求区间为多模式协同疏散，如图9（b）和图9（c）所示，临近风险源的出口路段被两种车辆共享的，使得不同疏散人员都有通道离开风险源，兼顾不同群体的疏散公平性。图9（c）中共享路段1-3 和2-3，公交车分别占用1车道和3车道，其余车道被小汽车使用，包含2 条反向车道。此外，载客量大但速度较慢的公交车优先使用最短路径，速度快的小汽车使用较长的路径，相互配合能有效降低整个系统的疏散总风险和网络清空时间。

4 结论

本文以最小化疏散总风险为目标，建立多模式疏散交通车队配置与车道分配协调优化的动态疏散优化模型，分析了多模式疏散系统的供需关系、疏散效率和疏散路径。通过案例验证得到如下结论：

（1）就疏散需求而言，在中等疏散需求下，组织多模式车队疏散优于单模式车队，能够进一步降低疏散总风险；多模式车队的最优公交车配置比例呈现离散变化现象并具有上限，本文上限值为0.49。

（2）就道路供给而言，受道路通行能力的限制，路网利用率存在上限，本文约为60%。因此，在制定交通疏散方案时，应识别道路网络中的瓶颈路段，充分利用瓶颈路段的通行能力，以提高整体路网的疏散效率。

（3）疏散总风险对疏散需求的变化比网络清空时间更敏感，应对高扩散性的灾害不能仅考虑疏散时间，应以疏散总风险最小为目标制定疏散预案。

（4）组织多模式疏散交通时，不同类型车辆共享的路段通常位于临近风险源的出口通道；将最短路优先分配给大容量的公交车能够显著降低疏散总风险。