周期性凸起结构对圆柱绕流流场及声场影响分析
王俊娇,冯和英*,,仝帆,王勇
(1. 湖南科技大学 机械设备健康维护湖南省重点实验室,湖南湘潭 411201;2. 中国空气动力研究与发展中心 气动噪声控制重点实验室,四川绵阳 621000)
钝体绕流作为一种普遍的流动现象广泛存在于风工程及航空航天等领域中。近年来,随着发动机降噪技术的不断进步,机体噪声成为飞机噪声中的一个重要因素,而在飞机进场过程中起落架噪声被认为是机体噪声的主要来源。然而起落架包含许多部件(如轮子、轴、液压线等),不同的部件之间的非定常流相互作用使得起落架的流场及声场难以预测。为了预测起落架不同部件的非定常流场及声场特性,研究者们将起落架分为多个声学元素,每个原件都被简化为一个圆柱体,通过串联圆柱简化起落架模型,体现其复杂的流动现象及气动噪声主要特征[1]。因此,单圆柱、多圆柱干涉(以串列双圆柱模型为主)的流场及声场的预测开始受到广泛的研究,同时也发展出了一些降噪控制手段。
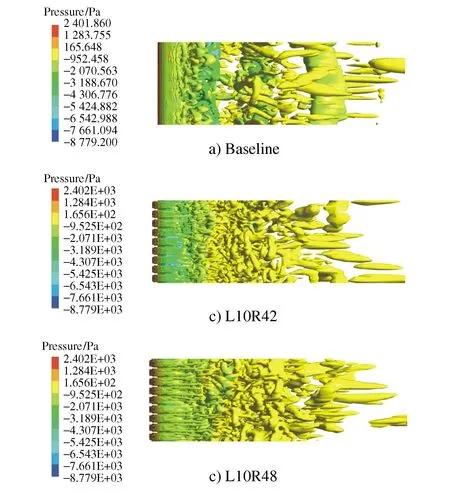
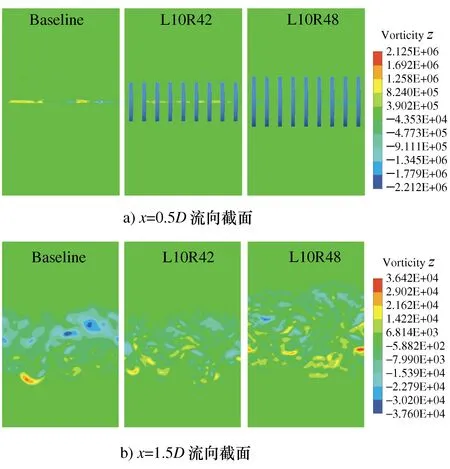
圆柱绕流流动现象被广泛研究[2-3],Zdravkovich[2]将光滑圆柱在均匀流中的流动分为层流、层流过渡、亚临界(在自由剪切层中过渡到湍流)、临界(在边界层中过渡到湍流)和完全湍流五种不同的流动状态。其中,亚临界状态雷诺数为(350~400) 为控制圆柱的涡脱落噪声,Schlinder等[4]研究了表面粗糙度对涡脱落噪声的影响。Sueki等[8]研究了多孔介质对圆柱绕流噪声的影响,取得了显著的降噪效果。魏峥等[9]对多孔介质控制圆柱尾迹进行了PIV实验,发现多孔介质可以降低涡脱落频率,抑制大尺度涡脱落,同时使涡脱落位置延后。Geyer[10]通过实验分析最佳多孔介质材料时,发现高孔隙率、低阻多孔材料的降噪效果更加显著。同济大学的陈羽等[11]研究了圆柱分离区布置多孔介质的降噪手段,结果表明在峰值及Sr=0.1~10之间的宽带噪声均具有良好的降噪效果。清华大学的朱文庆等[12]提出了圆柱周围布置阻尼网的降噪手段,应用在并列双圆柱模型上开展了降噪研究。Florence等[13]研究了雷诺数、表面粗糙度、自由湍流等对单圆柱和多圆柱模型噪声的影响,同时验证了两种降噪措施——凸起结构及钢丝缠绕对单圆柱和串联双圆柱模型噪声的影响,结果表明两种结构均可以用于显著降低噪声。 在先前的研究中,Florence等[13]提出了凸起结构与钢丝缠绕两个降低圆柱涡脱落噪声的概念,并在实验中验证了两者确实有显著降低涡脱落噪声的效果,但却并没有深入研究其降噪机理。同时Clark[14]提出的鳍状围栏的降噪手段与凸起结构很相似,基于Clark鳍状围栏高低对噪声的影响研究也尚不充分,其对流场和声场的影响机理需要进一步研究。 因此,本文采用LES(大涡模拟),结合FW-H方程的数值计算方法,研究圆柱表面周期性凸起结构中不同凸起直径对圆柱绕流涡脱落噪声的影响,进一步探索周期性凸起结构对圆柱绕流涡脱落噪声的影响及其物理机理。 以直径D=30 mm的圆柱为基准研究对象,对基准圆柱进行表面周期性凸起结构的建模,圆柱每隔一定周期设计一个厚度一定、直径更大的凸起结构。定义凸起间的周期L=10 mm不变,凸起厚度即展向长度为3 mm不变。记基准圆柱为Baseline,凸起结构直径为42 mm的为L10R42,凸起结构直径为48 mm的为L10R48。图1所示为L10R48模型的流向视图。 1.2.1 计算域与网格 图2a)为计算域示意图,其中圆柱中心距计算域的出口为40D,圆柱中心距计算域的进口及上下边界均为20D。同时为了控制网格数量,计算域的展向长度3D=90 mm,根据杜晓庆等[15]研究结合本文研究情况,此展向长度能有效模拟圆柱绕流的流动现象。图2b)为局部网格示意图,采用H-O-H型分块结构化网格,参考刘跃[16]的研究,考虑凸起结构直径的大小,本文在圆柱外周围3D范围内进行O型网格划分,其余部分均采用H型网格划分。为了保证计算的精度,在圆柱表面进行了网格加密,壁面第一层网格高度为0.000 1D,保证壁面y+<1,增长率为1.1。图2c)和图2d)分别为L10R48模型的流向与展向(一半)网格示意图。 图2 计算域及网格 1.2.2 流场及声场模拟方法 本文选择入口速度为60 m/s,马赫数约为0.176,基于直径的雷诺数为Re=1.23×105,可以视为不可压缩流动。采用Fluent作为求解器,选择基于SSTk-ω湍流模型对三维不可压的雷诺时均N-S方程组进行定常求解计算,压力与速度耦合采用SIMPLE算法,对流项选择二阶迎风格式。以定常流场作为初始场,采用LES方法进行非定常计算,其中LES中采用动力Smagorinsky-Lilly亚格子模型。非定常计算中,时间步长Δt=2×10-5s。参考文献[16],圆柱绕流的统计周期大于40个涡脱落周期,10个涡脱落周期作为统计收敛,本文流场推进5 000步后收敛,流场收敛后继续推进10 000时间步(60个以上的涡脱落周期)来获得流场统计平均结果。声场的模拟则在流场统计过程中通过Fluent中的FW-H方程声学模块进行计算。 计算域的左侧边界及上下边界设置为速度入口,右侧边界设置为压力出口,展向为平移周期边界条件,圆柱表面为绝热无滑移边界条件。 对于基准圆柱(Baseline)模型,本文设置了3套不同稀疏程度的网格进行非定常气动力的计算,来验证网格对计算结果的影响,具体计算结果如表1所示。其中,CD和Sr分别表示阻力系数和涡脱落对应的斯特劳哈尔数;网格1为稀网格,网格数量为213万,与实验值Sr之间的误差约为5%;网格2为中等密度网格,网格数量为405万,与实验值Sr之间的误差约为2.4%;网格3为密网格,网格数量为620万,与实验值Sr之间的误差约为1.9%;网格3相比网格2,计算精度差别不大,但是网格数量有所增加,考虑到计算时间的成本及计算的精度,Baseline模型选择中等密度网格2,认为网格已达到无关性要求。 表1 网格无关性验证 对于模型L10R42和L10R48,除凸起结构部分外,网格与模型Baseline基本一致。最后模型L10R42的网格数为477万,模型L10R48的网格数为509万。 网格无关性验证时仅对比了斯特劳哈尔数Sr,为进一步验证本文数值计算方法的正确性,图3为数值模拟圆柱表面压力系数(Cp)的平均值与文献[18]实验结果的对比,其中θ为方位角,以圆柱的驻点为起点,顺时针方向角度增大。从图3中可以看出,模拟结果与实验结果的趋势基本一致,且模拟值与实验值在整体上也吻合的比较好,个别角度误差在15%,少量角度的误差在5%左右,精度比较高,进一步验证了本文所选数值模拟方法和模型的合理性与计算精度。 图3 模拟与实验结果对比图 圆柱绕流的气动力系数可以表征圆柱绕流的流动现象,图4为3个模型整体升、阻力系数的最后5 000个时间步时程图。 图4 3个模型整体升、阻力系数时程图 图4中升力系数(CL)和阻力系数(CD)的定义分别为: (1) (2) 式中:ρ为空气密度;U为进口来流速度;S为圆柱表面在流向方向平面的投影面积;FL为圆柱表面升力;FD为圆柱表面阻力。 由图4a)可见,凸起结构显著影响了圆柱绕流的升力系数,3种模型升力系数波动有很大的差异。L10R42模型相对于Baseline模型来说升力系数的波动要小一半左右,而L10R48模型升力系数的波动仅为Baseline模型的1/5甚至到1/6的程度;同时需要注意的是,L10R42的升力系数周期性较差,而L10R48模型的升力系数更加缺乏周期性,这意味着48 mm直径的凸起结构已经打破了圆柱绕流的周期性流动现象。图4b)为3个模型的阻力系数的时程图,Baseline模型阻力系数最大,均值为1.492;L10R42模型阻力系数最小,均值为0.828;L10R48模型阻力系数与L10R42模型阻力系数的均值相差仅为0.097 2。 图5为基准圆柱模型与另外两个模型30 mm直径圆柱面部分截面的升阻力系数最后5 000个时间步时程图。图5a)可以发现,对于30 mm圆柱截面,L10R42模型的升力系数波动虽然有一定的降低,但是效果与图4a)中整体升力系数存在一定差距;而L10R48则依然有很好的降低效果;相比图4整体升阻力系数时程图,升力系数波动出现更大的差距,同样波动周期性不明显。图5b)的阻力系数时程图与图4b)的结论类似,数值上有一定的差异,L10R42模型与L10R48截面的阻力系数要比两个模型整体阻力系数要低,均值上要低0.2左右。 图5 基准圆柱与表面周期性凸起圆柱在30 mm直径处的截面升、阻力系数时程图 图6为基准圆柱模型与另外两个模型凸出部分截面的升阻力系数最后5 000个时间步时程图。图6a)与图4a)的结果很相似,同时与图5中30 mm圆柱截面升力系数的结论不同,升力系数的波动上L10R42模型降低要明显(此模型升力系数波动降低的主要原因是凸起结构截面上升力系数波动低)。图6b)与图4和图5中阻力系数关于均值大小的结论均相似,但是,凸出部分截面的阻力系数相对整体阻力系数反而有所增加,均值上增加了0.2左右。 图6 基准圆柱与表面周期性凸起圆柱凸起部分截面升阻力系数时程图 总体分析发现,周期性凸起结构可以有效降低圆柱表面升力系数波动,凸起直径更大的L10R48模型降低的更加显著,不同截面的升力系数脉动都得到了极大程度的降低;对于阻力系数,在均值上 L10R42模型降低了0.664,L10R48模型降低了0.567,不同截面的均值则与整体的均值相差不大。 图7为基准圆柱模型与两种凸起结构模型噪声结果的对比(即凸起结构的降噪效果)。在计算中,观察者(监测点)位于圆柱圆心正上方3.55 m处。图7a)为3个模型在90°方位角监测点的声压级频谱图,从图中可以看出,凸起结构的应用可以有效降低圆柱绕流的噪声;L10R42模型与L10R48模型在5 Hz~1 kHz的范围内基本上都可以降低噪声,其中L10R42模型在100 Hz以内的范围内,噪声比基准圆柱模型有所增加,L10R48则在100 Hz附近很小的范围内噪声有所增加,凸起直径更大的L10R48模型降噪效果要更加显著。同时,L10R42模型相比基准圆柱模型来说,尖峰值降低了约6 dB,L10R48最高的峰值则相对降低了19 dB左右;值得注意的是,L10R42模型的尖峰频率要比基准圆柱模型小约20 Hz,同时L10R48的频谱图中展现的峰值并没有明显的尖峰,存在几个小的尖峰与一个相对较大的尖峰。 图7 凸起结构降噪效果 图7b)则展示了3个模型在5 Hz~25 kHz范围内总声压级指向性,结果表明凸起结构的应用对噪声指向性的影响不大,且在此频率范围内,L10R42模型的总声压级比Baseline模型降低了约7 dB,L10R48模型的总声压级降低了19 dB左右。 根据涡声理论,低速流动时,可以认为流动声音产生的根源是涡。图8所示为3个模型在流向方向Q准则涡核等值面图,观察易知,两个凸起结构的应用都改变了基准圆柱模型典型的卡门涡的涡系结构,其中L10R42模型的涡系结构还存在和卡门涡街类似的周期现象,但其涡系结构相比基准圆柱模型而言要小、更集中一些;而对于L10R48模型来说,基本上已经观察不到卡门涡,涡系结构更小,且在圆柱的尾迹区纠缠在一起。外径更大的凸起结构观察不到周期性现象,这一定程度上解释了前文L10R48模型的声压级频谱图中没有出现明显单音噪声的原因。 图8 流向方向Q准则涡核等值面图(Q=1.18×106/s2) 图9为展向方向Q准则涡核等值面图,可以看出基准圆柱模型在展向方向有一个整体的涡;而凸起结构,将这个涡从开始就分成了一缕一缕的周期性涡结构,L10R42模型还不太明显,L10R48模型则能够明显观察到。 图9 展向方向Q准则涡核等值面图(Q=1.18×106/s2) 图10与图11分别为3个模型在两个不同流向位置上的总涡量与展向(z方向)涡量分布(图中x为圆柱中心到尾迹方向的距离)。从图10a)可以观察到,凸起结构的应用使得涡量得到了一定的衰减,且直径越大的凸起结构效果越明显;从图10b)可以看出,随着流动向下游的移动,凸起结构对流动的影响更加显著,基准圆柱下游大块的涡被凸起结构破碎成小涡,且凸起结构的直径越大,尾迹区中的小涡越碎、越多。图11也可以观察到凸起结构导致的展向涡量衰减、大涡破碎成小涡以及涡量聚集的现象,这一定程度上反映了凸起结构对涡系结构在流向及展向上的影响。 图10 3个模型的总涡量分布 图11 3个模型展向涡量的分布 综合以上分析可知,圆柱表面加周期性凸起结构的降噪机理在于,凸起结构打破了圆柱绕流脱落涡的连续性,破坏了典型的卡门涡街效应,连续的大涡被破碎成小涡,且较大的凸起结构外径能完全抑制周期性的涡脱落过程。 1) 在所研究的状态下,周期性凸起结构的应用能够明显降低圆柱表面升力系数的波动,直径更大的凸起结构降低的效果更加显著;而对于阻力系数,直径更大的凸起结构要比直径小的凸起结构稍大,但都比基准圆柱模型阻力系数有所减小。 2) 两种周期性凸起结构均能够有效降低圆柱绕流的涡脱落噪声,且直径更大的凸起结构降噪效果更加显著;同时,直径更大的凸起结构在降噪的同时,圆柱的涡脱落单一主频峰值噪声消失,变成多个更小的有一定差别的峰值噪声。 3) 周期性凸起结构的降噪机理在于,周期性凸起结构破坏了圆柱绕流脱落涡在展向方向的整体连续性,变成了更小尺度涡的涡脱落过程,抑制了大尺度展向涡的周期性脱落过程。1 研究对象及数值计算方法
1.1 研究对象
1.2 数值计算方法

2 计算模型验证
2.1 网格无关性验证
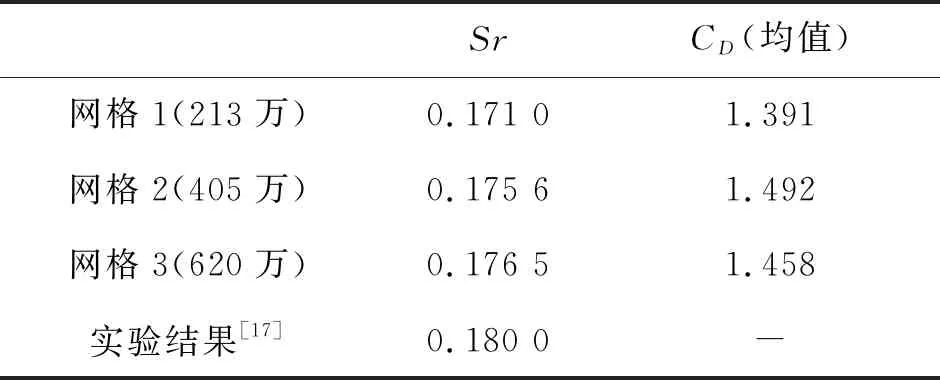
2.2 仿真结果验证

3 计算结果
3.1 流场结果



3.2 声场结果

3.3 降噪机理分析


4 结论

