高速冲击下钢索波动行为SPH模拟研究

赵明基,王发展,黄克鹏

(西安建筑科技大学 机电工程学院,西安 710055)

钢索的高速冲击是一种在极短时间内物体间发生的碰撞响应行为。冲击速度、碰撞角度和材料性能的变化使其波动特性以及冲击应力特征更为复杂,以现有实验和有限元等手段分析钢索高速碰撞响应机制尚存不足。光滑粒子流体动力学(Smoothed particle hydrodynamics, SPH)在冲击动力学领域处理大变形特征的动态响应问题中,具有不可替代的优势[1-3]。因此,利用SPH算法对钢索高速冲击问题进行深入探究,研究结果具有潜在的军用价值。

近年来,国内外学者采用SPH算法对高速冲击涉及的高应变率、大变形以及流动界面等问题进行了大量研究。Zhang和Liu等[4]将自适应光滑粒子流体动力学方法(ASPH)应用到具有材料强度的动力学问题中,并采用核函数修正法(KGC)对弹丸侵彻靶板问题进行模拟,但缓冲区的边界粒子的核函数可能会被边界截断,产生截断误差仍具有不稳定性。Sun等[5]将强可压缩多相SPH体积自适应从笛卡尔坐标系扩展到援助极坐标系来解决轴对称问题,但其无法计算拉伸力和剪切力。Wang等[6]采用FEM-SPH耦合方法对强夯引起的直流大变形问题进行数值分析,但该方法在三维计算中较为复杂,精度不高。Markauskas和Kruggel-emden[7]采用DEM-SPH耦合方法对湿法连续筛分进行了数值分析,提出了一种新的表征屏蔽表面的简单模型,但其无法解决因为粒子缺失而带来的能量损失问题。Riccardo等[8]采用SPH-FE耦合法对陶瓷基弹道盾牌高速冲击问题进行模拟,但无法解决表面张力不稳定问题。Young等[9]提出了一种新的SPH全拉格朗日公式与欧拉公式耦合方法,实现了全拉格朗日公式自适应转换为欧拉公式,并采用此方法对斑片进行二维和三维高速冲击模拟,但此方法未能解决拉伸不稳定问题。Varas等[10-12]基于SPH-ALE耦合法建立有限元模型,研究了不同冲击速度、不同充液比例对油箱毁伤效应的影响,但此方法不能较好的解决三维高速碰撞问题。以上作者的研究,均为SPH算法在高速冲击问题中提供了有效的数值模拟手段,但仍存在计算效率低、拉伸不稳定、边界条件处理难和易产生零能模式等缺陷。但是,国内外基于SPH法对钢索在高速冲击下的瞬态响应研究未见报道。

为了利用SPH算法对高速冲击下的钢索波动行为进行数值模拟,选取Monaghan型人工粘性方程有效解决了粒子飞溅问题,采用镜像粒子法消除了粒子缺失的现象,建立了钢索高速冲击的动力学模型,揭示并掌握了其动态特性和瞬态响应规律,通过与FEM算法对比表明SPH算法所建立模型的高效性与优越性。理论结果验证了仿真所建模型的准确性,为钢索高速冲击中应用提供了理论参考。

1 SPH方法

光滑粒子流体动力学是一种流动质点无网格方法,它将计算域离散成一系列承载着各种物理量的粒子,且粒子间通过核函数相互作用,使数值模拟时不会受到空间任意分布粒子的影响。相对于传统的网格数值方法,在处理大变形、交界面位置捕捉、解决不连续性问题方面具有先天优势[13]。

1.1 控制方程

高速冲击时固体材料会表现出流体的性质,故基于核近似和粒子近似原理对描述冲击问题的控制方程进行粒子近似,可以得到具有材料强度的流体动力学控制方程的SPH形式[14],即:

(1)

1.2 人工粘性

为有效防止粒子间靠近时的非物理穿透现象,减少数值耗散,采用Monaghan型人工粘性方程[15],具体方程如下:

(2)

(3)

其中:

(4)

式中:A、B为标准常数,且与A相关的项得到的是体积粘度,与B相关的项是用于防止高马赫数粒子的相互穿透;c为声速的速度矢量;v为粒子的速度矢量;φ用于防止粒子间相互靠近时产生的数值发散。

1.3 边界条件

为解决临近边界粒子点积分区域被截断的问题,本文引入镜像粒子法来处理边界问题,使其满足物面边界条件。

粒子镜像处理过程如图1所示。其中,i粒子为正在进行镜像操作的粒子,j粒子为镜像粒子。通常,i粒子与j粒子密度和压力相同,使求解域内实粒子在固壁边界处法向不穿透和切向可滑移。

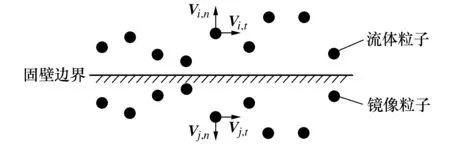
图1 镜像粒子法

二者的速度满足以下关系:

(5)

在镜像粒子法中关于应力张量的组成部分f的边界修正式为

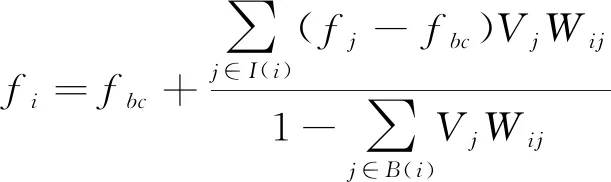
(6)

式中:fbc为边界粒子在x=xi处预设的边界张量;Wij为插值核函数。

2 模型建立

2.1 网格模型

本文采用LS-PrePost软件对直径10 mm,长度1 000 mm的钢索和直径30 mm,高50 mm的圆柱形刚体进行建模,利用SPH-Generation在钢索宽、高方向各设10个粒子,长度方向设置10 000个粒子,粒子间距为1.2 mm,模型共80 000个粒子,使用SolidMesher对刚体进行网格自由划分,如图2所示。

图2 网格模型

2.2 材料模型

由于钢索实际上是由长细比很大的钢丝绳和其他复合材料拧结而成,综合性能等效于钢材料,故采用Elastic-Plastic-Hydro材料模型结合Mie-Gruneisen状态方程来表征其性能,设置密度为7.80 g/cm3,弹性模量E为210 GPa,剪切模量G为80 GPa。其次采用RIGID表征刚体材料性能,设置密度为7.83 g/cm3。

对于金属大变形可引用Mie-Gruneisen状态方程[16-17],定义压力为

(7)

式中:pH为冲击Hugoniot曲线上的点的压力;Γ为Gruneisen参数。

(8)

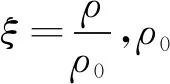
对于不同金属材料的状态方程参数如表1所示。

表1 不同金属材料Mie-Gruneisen状态方程中的参数

2.3 边界设置

将SPH粒子设为从节点,有限元与SPH粒子连接处的单元表面设为主表面。刚体速度设置为260 m/s、270 m/s 、280 m/s、290 m/s和300 m/s,冲击角度设置为75°、80°、85°和90°,作用时间设置为200 μs,冲击点与钢索的摩擦因数设置为0.5、0.6、0.7和0.8,刚体与钢索接触类型为侵蚀接触。

2.4 仿真结果与分析

2.4.1 主应力矢量分布

随着刚体高速冲击钢索时,导致钢索应力分布不均,通过分析主应力的变化趋势,得到粒子受力规律。图3为在冲击速度为260 m/s冲击下不同时刻钢索的主应力矢量分布图。

图3 不同时刻下钢索的主应力矢量分布

由图3a)可知,当t=14 μs时,由于受到高速冲击力作用,钢索中心开始产生形变,钢索内部应力较大,钢索中心处内外两侧部分粒子产生与其他粒子相反的主应力;由图3b)可知,当t=34 μs时,钢索中心外侧应力较大并开始产生断裂,波峰处粒子产生的主应力比其他部位粒子大,且相切于应力传递方向;由图3c)可知,当t=70 μs时,钢索内所有粒子均受到应力,钢索中心处内侧部分粒子产生反应力,且绝对值大于其他部位粒子;由图3d)可知,当t=112 μs时,钢索完全断裂,粒子产生的主应力减小,中心处粒子主应力方向指向冲击方向。

2.4.2 结构强度分布

在钢索高速冲击过程中,由于冲击力的瞬间作用,导致钢索受力不均,粒子分布离散,使得钢索结构强度改变。图4为在冲击速度为260 m/s冲击下不同时刻钢索的整体结构强度分布。

图4 不同时刻下钢索的整体结构强度分布

由图4a)可知,当t=14 μs时,钢索粒子开始受冲击力作用,大量粒子由内向外发散,导致粒子相互挤压,部分粒子产生反向作用力,使中心结构强度增加;由图4b)可知,当t=34 μs时,钢索外侧开始断裂,钢索中心带粒子呈圆弧状分布,随着应力波向两端传递,粒子从中心向两端分散,且分布对称,使中心结构强度锐减;由图4c)可知,当t=70 μs时,钢索内侧未断裂,钢索中心处粒子受力增大,且向内外两侧发散,反作用力由外向内逐渐增大,钢索强度逐渐减小;由图4d)可知,当t=112 μs时,钢索内外两侧完全断裂,钢索中心处粒子受力锐减,且沿中心向四周发散,钢索强度降至最低。

2.4.3 影响因素分析

在摩擦因数μ=0.7不变条件下,分别选取不同冲击角度θ,在冲击角度θ=85°不变条件下,分别选取不同摩擦因数μ,分析不同摩擦因数与冲击角度对钢索冲击应力的影响。图5为不同冲击角度下冲击速度与钢索冲击应力大小的关系,图6为不同摩擦因数下冲击速度与钢索冲击应力大小的关系。

图5 不同冲击角度下冲击速度与钢索冲击应力大小的关系

图6 不同摩擦因数下冲击速度与钢索冲击应力大小的关系

如图5所示,滑动冲击下钢索第一次冲击应力随着冲击角度的增大而减小,其差值随着冲击速度的增加而增大。如图6所示,滑动冲击下钢索第一次冲击应力大小随着摩擦因数的增大而增大,其差值随着冲击速度的增加而增大,且增幅较为明显。

3 SPH与FEM算法对比分析

3.1 系统总能量

本文进行的数值仿真中系统总能量是指内能、动能、接触面滑移能、沙漏能、系统阻尼能和刚性墙能的总和,图7为在不同算法下不同冲击速度的系统总能量-时间历程曲线。

图7 在不同算法下不同冲击速度的系统总能量-时间历程曲线

由图7a)可知,当t=0～17 μs时,钢索与圆柱体尚未接触,故系统总能量不变;当t=17～60 μs时,系统总能量迅速减少;当t=60～180 μs时,系统总能量仍减少,但其速率明显下降;当t=180～200 μs时,系统总能量趋于稳定。

由图7b)可知,当t=0～17 μs时,系统总能量不变;当t=17～20 μs时,系统总能量骤减;当t=20～80 μs时,系统总能量微小波动,但总体呈下降趋势;当t=80～110 μs时,系统总能量趋于稳定;当t=110～200 μs时,系统总能量缓慢增加。

由图7a)和图7b)仿真结果对比可知,系统在SPH算法与FEM算法下均有能量损失,且冲击速度越大能量损失越大。由于粒子的相互作用以及粒子与单元间接触算法,造成系统的能量损失,但SPH算法的能量损失要略少于FEM算法。一方面是由于本文刚体采用了网格划分的方法,因此模型总粒子数要比纯SPH算法的粒子数少;另一方面是由于粒子与单元接触算法造成的能量损失要远小于粒子间相互作用的能量损失。

3.2 应力波分布

在高速冲击过程中,钢索由直线预紧状态转为三角形布局的应力传播状态为弯折波。弯折波的传播速度很大,但钢索应力的传播速度要远大于弯折波,因此钢索中任一点的运动都是从应力传递到该点的时刻开始。由于刚体与钢索的相互作用等效于两物体间的刚性碰撞,所以二者在啮合处存在高频率和大幅度的接触力,使各处应力和应变不是均匀分布的,图8和图9分别为采用SPH算法和FEM算法在冲击速度260 m/s冲击下不同时刻下钢索的范式应力云图。

图8 不同时刻下钢索的Mises应力分布(SPH算法)

初期的拦阻动力学特性主要体现于钢索本身。在刚体刚与钢索接触的时候,钢索两端无法在短时间内进行动作,因此在碰撞初期钢索的应力是由刚体与钢索系统相互作用产生的,故钢索边界状态对整个碰撞过程所产生的影响可忽略。

由图8a)～图8c)可知,在高速冲击下,在t=14 μs时,钢索中心处由内至外产生形变,随着时间推移,应力以波的形式由中心向两端传递;在t=34 μs时,钢索在外侧开始产生断裂,并向内侧延展,但应力波依旧向两端传递;在t=94 μs时,钢索内外两侧完全断裂,但应力波依旧向两端传递,并不断进行着反射叠加。

由图9a)～图9c)可知,在高速冲击下,在t=14 μs时,钢索中心处由内至外产生形变,随着时间推移,应力以波的形式由中心向两端传递;在t=34 μs时,钢索外侧达到断裂极限,但由于网格的限制,钢索外次没有产生断裂,应力波一直在钢索内传递并不断进行着反射叠加。

由图8与图9对比可知,采用FEM算法进行的仿真形变没有SPH算法明显,无法完全仿真出弹性性能。若网格划分过大,则会因为网格畸变导致计算终止;若网格划分过小,则会仅为计算单元过多导致计算时间过长,效率比SPH算法低。故采用SPH算法对钢索高速冲击动力学进行数值模拟比传统网格分析计算精度高,效率高,表明了SPH算法在处理大变形、解决不连续性问题方面的优越性。

4 理论及结果对比

4.1 钢索波动理论

由于设置的冲击角度为90°,且初始应力σ0远小于由于冲击而产生的新应力σ,可以将波动模型的理论公式简化,即:

(9)

(10)

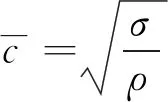
(11)

(12)

(13)

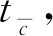
4.2 对比验证

为了验证SPH算法在模拟钢索的波动特性上的准确性,本文通过对钢索波动参数的理论值和仿真值进行对比。表2和表3分别为采用SPH算法和FEM算法对钢索在不同冲击速度下的波动参数的仿真值与理论值的对比结果。

表2 不同冲击速度下的钢索波动参数(SPH算法)

表3 不同冲击速度下的钢索波动参数(FEM算法)

由表2可知,在LS-DYNA中用SPH算法得到不同冲击速度下的纵波、横波和弯折波的波速均比理论值要小,这是由于钢索波动性理论分析中没有考虑钢索内部阻尼。对比可知,SPH算法下的理论值与仿真值高度一致,误差均在6%以内,而FEM算法下的误差在10%左右。从而验证了仿真所建模型的准确性与优越性。

5 结论

为研究高速冲击下钢索应力波的传播规律,建立了特殊连续弹性体模型,通过人工黏性与镜像粒子法相结合,解决了钢索数值模拟中粒子飞溅和粒子缺失的问题,分别利用SPH算法和FEM算法对钢索高速冲击过程进行数值模拟,得到如下结论:

1) 在高速冲击下,钢索中心处由内至外产生形变,随时间推移,应力波由中心向两端传递,并产生反射叠加现象。通过SPH算法与FEM算法对比可知,二者系统总能量损耗相似,同时采用SPH算法对高速冲击下钢索波动行为进行数值模拟计算精度更高,效率更高。

2) 在高速冲击作用下,钢索内外两侧部分粒子产生反应力,中心处粒子由内向外发散,结构强度增加;钢索中心处外侧产生断裂时,波峰处粒子产生较大主应力,且相切于应力传递方向,中心带粒子呈圆弧状分布,粒子向两端分散,结构强度锐减;钢索中心内侧未断裂时,所有粒子均受到应力作用,且内侧部分粒子产生绝对值较大的反应力,粒子整体向内外两侧发散,结构强度减小;钢索完全断裂后,中心处粒子主应力方向指向冲击方向,粒子沿中心向四周发散,结构强度降至最低。

3) 滑动冲击下钢索冲击应力随冲击角度的增大而减小,随摩擦因数的增大而增大,其差值随着冲击速度的增加而增大。通过理论验证了模型的正确性,为钢索的设计与优化提供理论参考。