Crushing behaviors of buckling-induced metallic meta-lattice structures

Jin-hu Dong ,Yong-jun Wng ,Feng-nin Jin ,Hu-lin Fn b,,*

a State Key Laboratory for Disaster Prevention & Mitigation of Explosion & Impact,Army Engineering University of PLA,Nanjing,210007,China

b Department of Civil Engineering,Nanyang Institute of Technology,Nanyang,473004,China

c State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,China

Keywords:Buckling induced meta-lattice structure(BIMS)Crushing force efficiency

ABSTRACT Thin-walled lattice materials can be applied as energy absorbers in protective structures of civil defense.In this paper,quasi-static in-plane crushing tests were carried out to investigate the crushing behavior and energy absorption of buckling induced meta-lattice structures(BIMSs) with different central angles made of plastic iron material DT3 and formed by wire cutting technique.Three crushing patterns were revealed and analyzed.The test results clearly show that the initial peak force (IPF),the crushing force efficiency (CFE),the specific energy absorption (SEA) and the mean crushing force (MCF) can be substantially improved by introducing buckling pattern into the straight-walled lattice structure.The MCF of the BIMS was consistently predicted based on the simplified super folding element (SSFE) and the flattening element.

1.Introduction

Recently hierarchical tubes [1-3],honeycomb structures [4,5]and lattice structures[6-8] have been widely used in engineering for their excellent mechanical properties,such as high specific strength and high specific energy absorption (SEA).

Lattice structure is a kind of cellular structure composed of ordered periodic cells [9,10].Many studies were devoted to investigate their deformation modes and energy absorption (EA)capacities.Ozdemir et al.[11,12]studied the compressive behaviors of cubic,diamond,and re-entrant cubic lattice structures under quasi-static and dynamic conditions.They found the initial peak force(IPF)of cubic,diamond and re-entrant lattice structures were very large,and the force displacement curve decreases rapidly after exceeding the initial peak force.Habib et al.[13]investigated quasistatic EA of six polymeric lattice structures of different cellular topologies.They found that bending-dominated structures have low stiffness and strength but provide good EA capability.Stretching dominated structures are stiffer and stronger but have low EA performance.Davami et al.[14] investigated the behaviors of shape-recovering lattice structures and revealed the loading rate of the plastic deformation.They concluded that additive manufacturing would be a versatile tool to create structures with complex geometries for EA.Bian et al.[15]investigated the effect of the detailed lattice orientation on the EA performance and developed theoretical models to evaluate the EA of these lattice structures.Li et al.[16]investigated the in-plane crushing resistance and EA of different polycrystalline-like (PL) lattice structures.They thought the improvements in the mean crushing force (MCF) and the SEA would originate from the grain boundaries of the PL lattice structures which could restrain the evolution of the shear bands and change the shear failure mode into a layer-by-layer progressive crushing mode.Through the above literature review,it can be seen that with the development of the manufacturing technology,many different types of lattice structures have been manufactured and studied,but there are few studies on buckling induced meta-lattice structures.

Similarly,a large number of studies have focused on the square grids [17-19].Qiu et al.[20,21] looked the square grids as membrane-dominated structures.The force-displacement curve of the membrane-dominated structure has an IPF followed by a rapid drop to much lower values.In order to reduce the IPF of the square grid,Wang et al.[22] introduced curved cell walls into the square grids.They have numerically and experimentally studied the buckling behaviors of these grids.However,few efforts were paid to study the crushing pattern and the EA of these curved-walled grids under large deformation.

In this research,a new type of buckling-induced meta-lattice structure(BIMS)made of plastic iron material DT3 by wire cutting technique was designed,tested and analyzed.The EA,the MCF and the CFE of the BIMS with different central angle were discussed.Based on four simplified super folding elements (SSFEs) and a flattening element,the MCF of the BIMS was predicted.

2.Structural design and manufacture

The cell diagram of the BIMS is displayed in Fig.1.The topology is named as bending-dominated periodic lattice by Wang et al.[22].The thickness of the meta-lattice plate,T,is 16 mm.The height of the BIMS,H,is 82 mm.The length of each strut,L,is 16 mm and the thickness of the rod,t,is 2 mm.The central angle is represented by α,which controls the amplitude of the waviness.The central angle changes from 0,30,45,60,90to 120in this research.All specimens were made by wire cutting technology.The material used in this paper is pure electrical iron called DT3.This kind of metal has a super ductility,and there would no fracture in the inplane compression test.The engineering stress-strain curve of iron DT3 is shown in Fig.2.The yield strength of the DT3 is 150.43 MPa,the ultimate strength is 263.59 MPa.The density of DT3 is 7.8 g/cmand the fracture strain is 0.425.

3.Quasi-static in-plane compression experiments

Six groups of BIMSs were made and three testing samples were prepared for each group.A 20-ton universal testing machine was used to carry out the quasi-static in-plane compression tests.The top platen and the testing machine were connected by ball hinge.The bottom platen was fixed on the test platform with bolts.The specimens were compressed at a loading rate of 2 mm/min.

3.1.Crushing performances

Three load-displacement curves and three crushing patterns were revealed,changing from layer-by-layer crushing pattern,hybrid crushing pattern to simultaneous crushing pattern accompanying with central angle improving from 0to 120,as shown in Figs.3 and 4.Compared with the structure printed by the brittle material PLA,the structure made by the plastic material is roughly the same in the total failure mode,which are the same three failure modes.However,the angle critical value of failure mode transition is different.The angle critical value of plastic material is higher than that of brittle material.

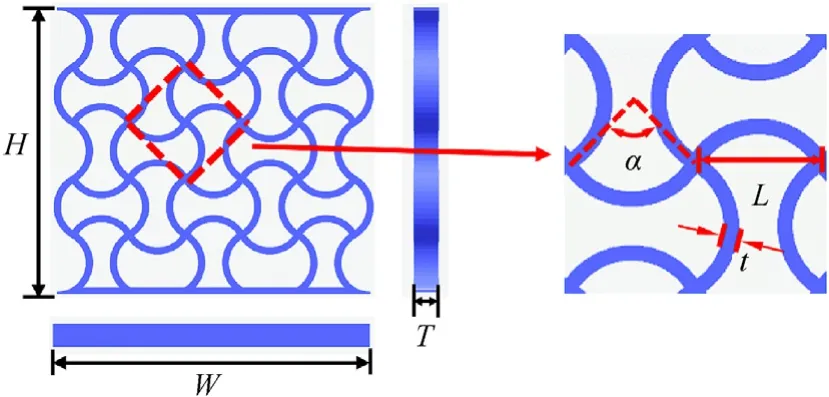
Fig.1.Designing BIMS through introducing buckling mode into straight-walled lattice[22].

Fig.2.Tensile stress-strain curve of iron DT3.

When the strut curvature is small,(that is,when the central angle is small),the lattices will be crushed layer-by-layer.The forcedisplacement curves have dramatic zigzag jumps,as shown in Fig.3(a)-(c).The crushing process of the BIMS can be divided into four stages,as shown in Fig.4(a)-(c).In the first stage,one layer of the upper two layers and one layer of the lower two layers appear buckling at the same time,and each strut forms plastic hinges at the upper and lower ends.Then these two layers of struts bend and fold around the plastic hinges,and the folding distance is about the height of two layers of struts.In the second stage,the upper two layers and the lower two layers begin to bend at the same time.And the two layers of struts fold as the folding in the first stage.In the third stage,the middle layer of struts buckle.Different from the first two stages,each strut in the middle layer mostly produces three plastic hinges at the upper and lower ends and the middle of the strut.In the fourth stage,all layers are compressed and deform together,gradually being compacted with a rising forcedisplacement curve.

When the central angle is increased to 60and 90,the waviness of the strut changes the crushing pattern.The crushing curve is more stable accompanying with zig-zags,as shown in Fig.3(d)and(e).The crushing process of the BIMS can be divided into four stages,as shown in Fig.4(d) and (e).In the first stage,the middle three layers bend at the same time,and a total of two plastic hinges are generated at the upper or lower end and the middle part of each layer.With the increase of the displacement,the middle three layers of struts bend and fold around their respective plastic hinges.In the second stage,the upper and lower layers bend.Unlike in the first stage,the upper and lower layers of struts in this stage produce two or three plastic hinge and then fold.In the third stage,all the layers compress and deform together,gradually being compacted with an upward curve on the force-displacement curve.The IPF is further reduced.It is a hybrid crushing mode.

Further increasing the central angle,the curved struts completely change the crushing pattern into simultaneous crushing pattern.The force-displacement curves have three typical stages: elastic deformation,ascending stage and densification,as shown in Fig.3(f).The IPF is further reduced.The curves are smooth with soft zigzags.All the five layers were almost crushed simultaneously.Plastic hinges formed in the crushing,as shown in Fig.4(f).After contact,the horizontal struts will be flattened and more energy will be absorbed.

Fig.3.Force-displacement curves of BIMSs with different curvature (central angle): (a) 0°,(b) 30°,(c) 45°,(d) 60°,(e) 90° and (f) 120°.

3.2.Negative Poisson's ratio

As shown in Fig.5(a),the BIMS has negative Poisson's ratio in the compression.It is easily found that when the BIMS is compressed in the Y direction,the odd layers of the structure are also compressed.Fig.5(a)clearly show the selected reference point position.The strain in the y direction only considers the strain in the y direction of the overall structure,that is,the strain between the upper and lower horizontal planes.And the midpoint of the outermost wall of each layer is selected as the reference point to calculate the five sets of strains in the x direction.Fig.5(b)-(f)reveal the development of the equivalent strains of the BIMS.

As shown in Fig.6,initially,the Poisson's ratio of the central layer exceeds -1.5.With the decrease of the strain in Y direction,the strain in X direction increases gradually.The Poisson's ratio of the even layers even transforms from negative to positive.

Transverse contraction and longitudinal compression change the configuration of the meta-cellular structure,as shown in Fig.7.Before compression,the meta-cellular structure is a square cell with four curved walls.In compression,accompanying with the transverse contraction and the longitudinal compression,neighboring struts gradually contact with each other.After strut contact,the representative curved-walled square cell turns to two curvedwalled triangular cells.As the triangular cell is a statically determinate structure,the Poisson's ratio changes to positive and the crushing force will be enhanced.

Fig.4.Crushing processes of BIMSs with different curvature (central angle): (a) 0°,(b) 30°,(c) 45°,(d) 60°,(e) 90° and (f) 120°.

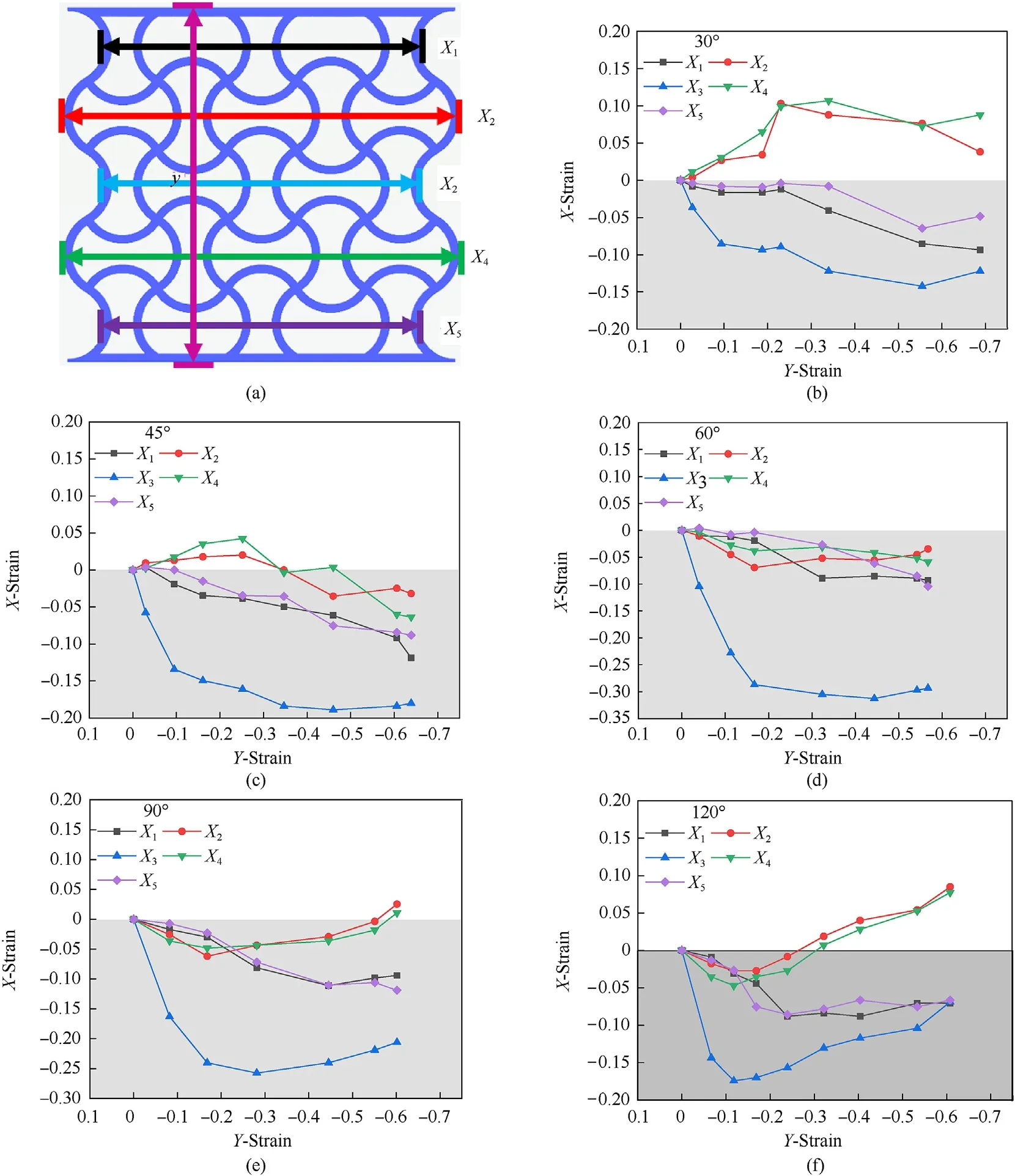
Fig.5.(a) Schematic diagram of selection of strain points and strain development in crushing for BIMSs with central angle of (b) 30°,(c) 45°,(d) 60°,(e) 90° and (f) 120°.

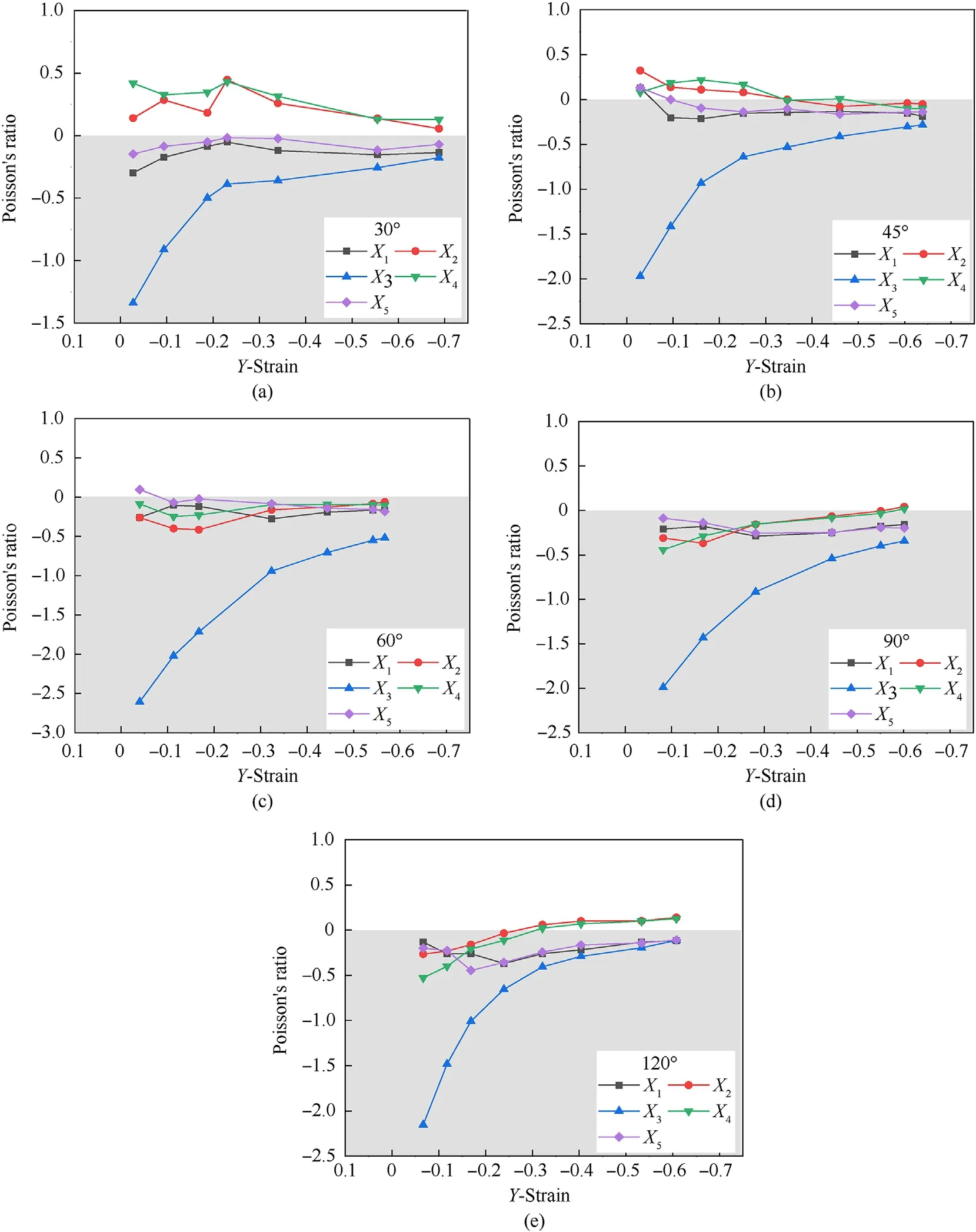
Fig.6.Poisson's ratio development in crushing for BIMSs with central angle of (a) 30°,(b) 45°,(c) 60°,(d) 90° and (e) 120°.

Fig.7.Structural evolution and Poisson's ratio transformation.

4.Structural crashworthiness evaluation

The displacement corresponding to the force equal to the average IPF of the straight-walled lattice structures in densification is selected as the effective crushing distance(ECD)to calculate the EA.The EA indexes are listed in Table 1 in details to evaluate the EA performance.

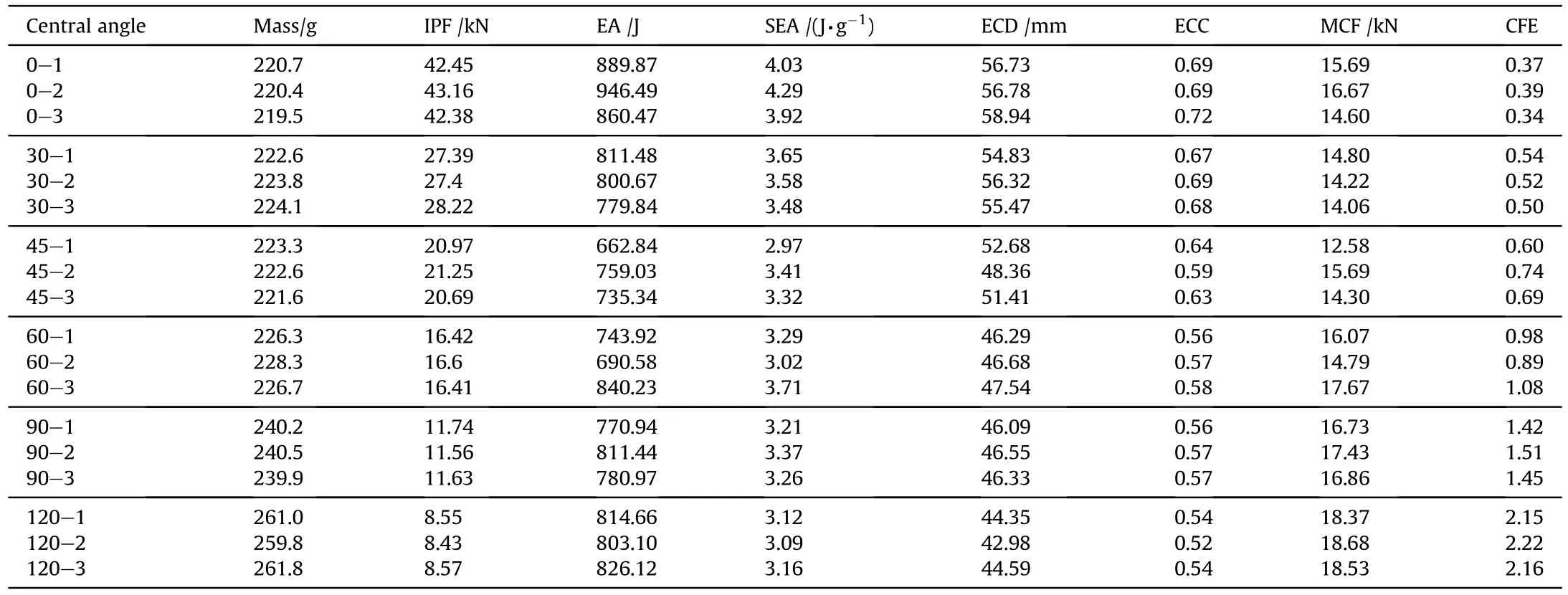
Table 1.EA indexes of BIMSs with different central angles.

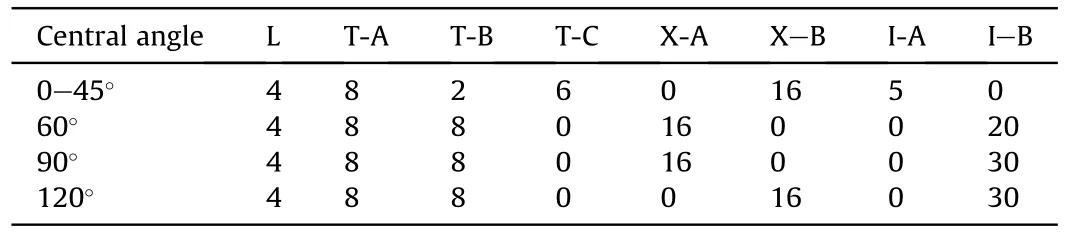
Table 2.Basic folding elements of BIMSs.

With the increase of the central angle,the ECD of the BIMS is continuously reduced from 0.70 to 0.53,a decrease of 24.29 %.As shown in Fig.8(a),the IPF of the BIMS is greatly reduced from 42.66 kN to 8.52 kN,a decrease of 80.03 %.

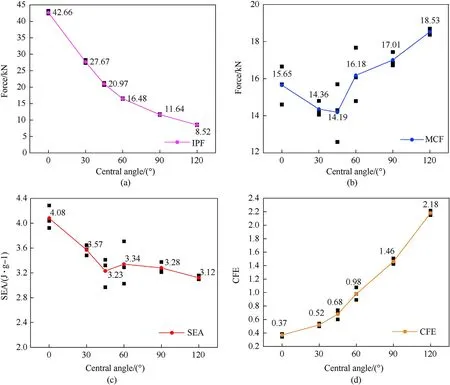
Fig.8.(a) Initial peak force,(b) Mean crushing force,(c) Specific energy absorption and (d) Crushing force efficiency of BIMSs.

With the increase of the center angle,the MCF first decreases and then increases,as compared in Fig.8(b).Similarly,the SEA of the BIMS is slightly decreased from 4.08 J/g of straight-walled lattice to 3.12 J/g of BIMS with central angle of 120,as compared in Fig.8(c).However,when the angle increases to more than 60,the SEA tends to a stable value.

Introducing buckling mode into the lattice structure,the CFE of the lattice structure is remarkably improved,as shown in Fig.8(d).It is nearly proportional to the central angle,increasing from 0.37 at 0to 2.18 at 120.The CFE is tightly relating to the crushing pattern.Lattice with layer-by-layer crushing mode has CFE smaller than 0.74.Lattice with hybrid crushing mode has CFE from 0.89 to 1.51.The CFE of BIMSs with simultaneous crushing mode is close to or even much larger than 2.0.

5.Theoretical analysis

5.1.Basic folding element

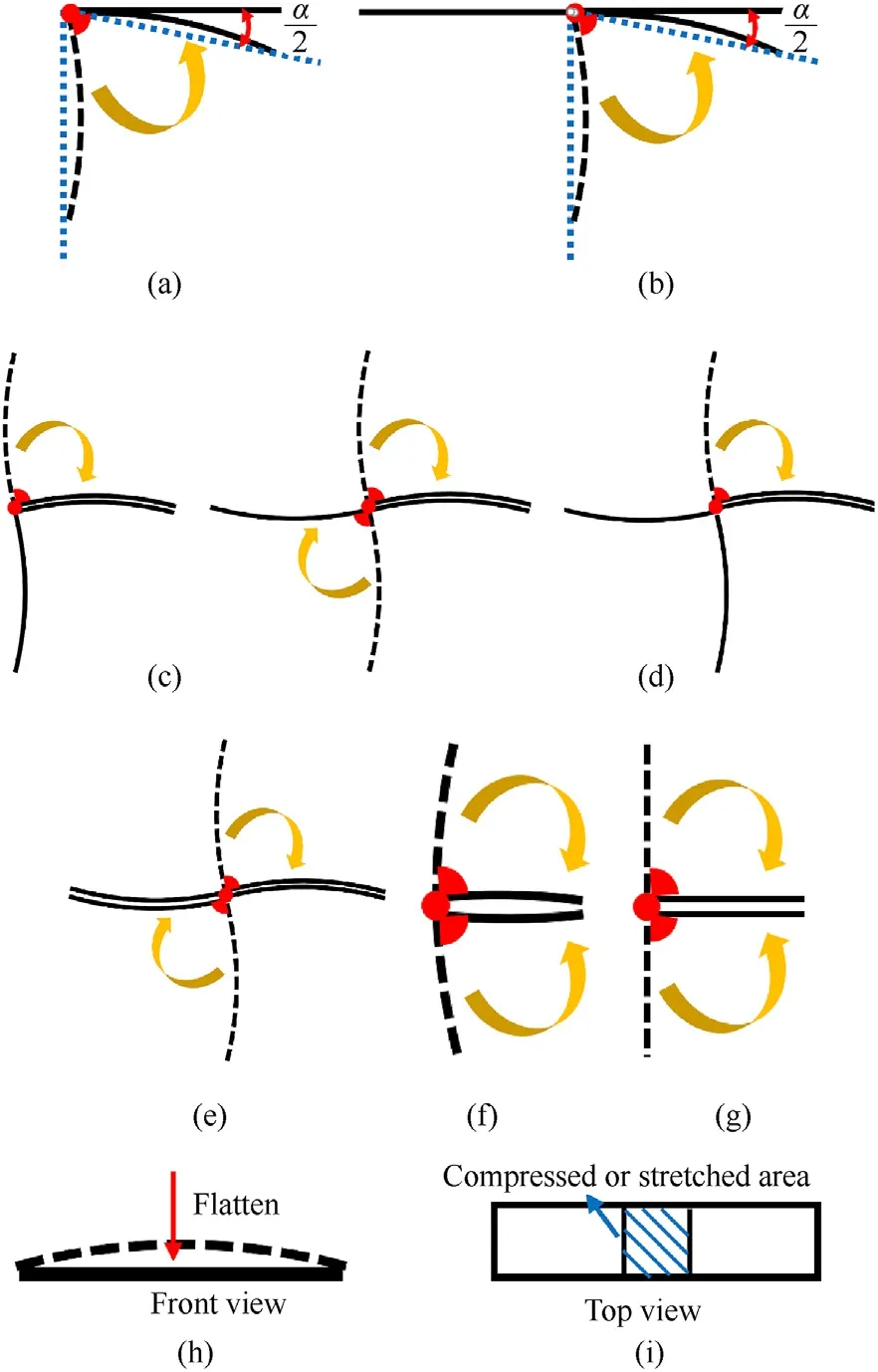
Fig.9.(a)Corner element L,(b)T-shaped element T-A,(c)T-shaped element T-B,(d)Tshaped element T-C,(e) X-shaped element X-A,(f) X-shaped element X-B and (g) Ishaped element I-A,(h) I-shaped element I-B and (i) flatten element F.

When the angle exceeds 60,as shown in Fig.9(i),the flattening energy Emust be considered and calculated by

5.2.MCF of BIMSs

In the crushing process,the work done by the MCF is equal to the energy absorbed by the basic folding element.And the distribution of the basic folding elements are listed in Table 2.

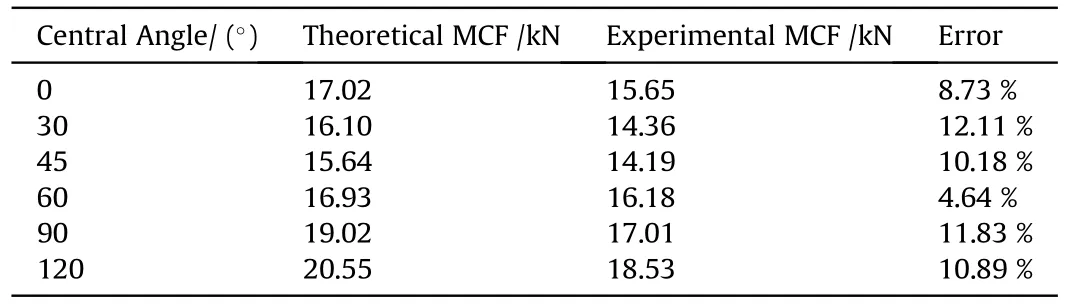
Table 3.MCF comparisons between theoretical predictions and experimental values.

For the meta-lattice structure with small central angle,(i.e.0,30and 45),the crushing mode is layer-by-layer.The MCF of these BIMSs,Pis given by

where H is the length of the lattice structure and n is the number of cells on each side.For the meta-lattice structure with larger central angle,(i.e.60and 90),the crushing mode is hybrid.The MCFs of these BIMSs,Pand Pare given by

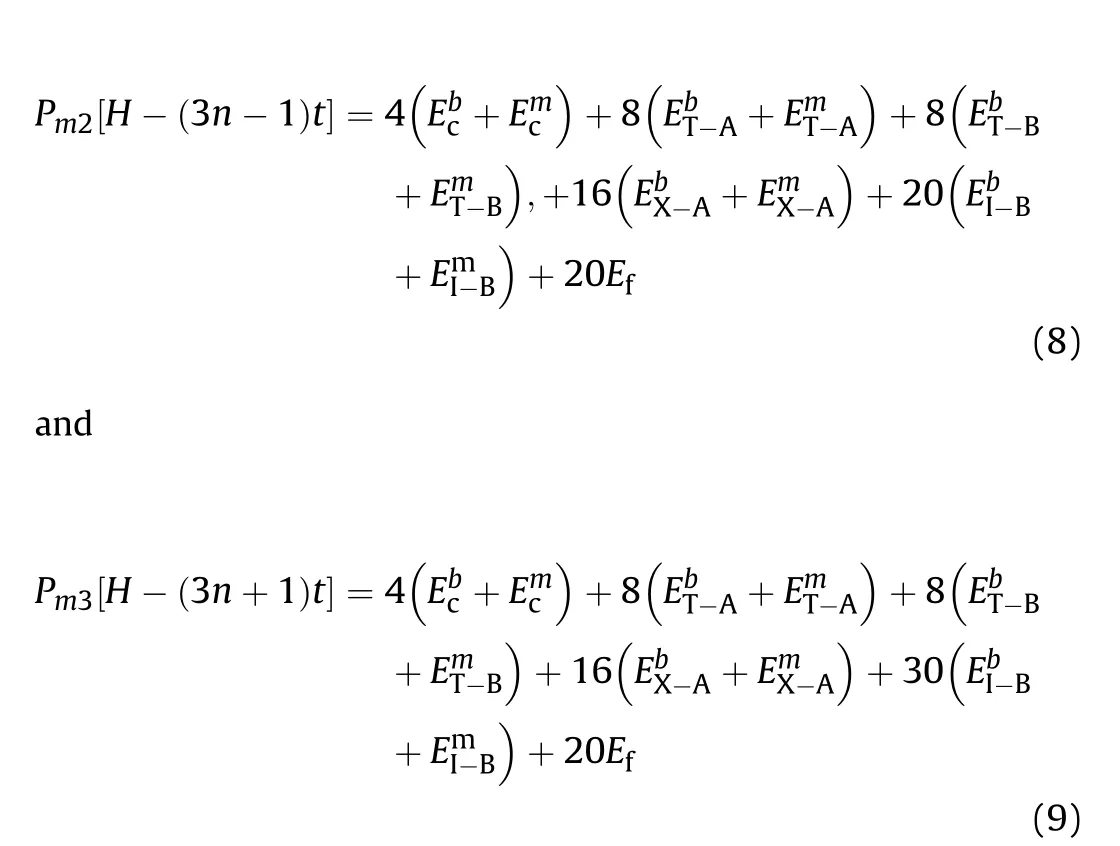
For the meta-lattice structure with central angle of 120,its crushing mode is simultaneous crushing pattern.The MCF of the BIMS,Pis given by

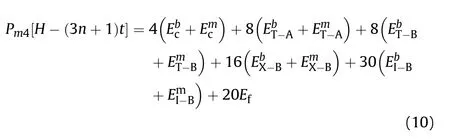
It can be seen from Table 3 that the maximum error between the theoretical MCF and the experimental value is 12.11 %.And the theoretical value is generally larger than the experimental value.During the theoretical derivation,in order to simplify the calculation,we assume that the structure is completely folded.But this is very difficult to do in the process of experiment.For example,the plastic hinge is supposed to turn 90in theory,but it does not reach 90in the actual test.This assumption leads to the fact that the calculated bending energy of the plastic hinge is smaller than the experimental value.Similarly,the energy dissipated by the flattening mechanism calculated theoretically is smaller than the experimental value.Therefore,for example,formula (10),the calculated values of energy dissipated by the two mechanisms on the right side of the equation are larger than the experimental values.Although the crushing distance on the left side of the equation will be smaller than the experimental value,it can be ignored.Therefore,the MCF calculated based on the theory of simplified super folding element and flattening element is acceptable.

6.Conclusions

According to the research,introducing buckling pattern into straight-walled lattice structures can construct meta-lattice structures with negative Poisson's ratio and substantially modify the crushing pattern and the EA performance.

Compared with BIMSs printed by PLA,strut fracture is avoided and the metallic BIMS exhibits more excellent ductility.

The crushing pattern is changed by the buckling topology.The auxetic BIMS made of iron DT3 with excellent plasticity has three typical crushing patterns,including layer-by-layer crushing pattern of BIMSs with central angle of 0,30and 45,hybrid crushing pattern of BIMSs with central angle of 60and 90,and simultaneous crushing pattern of BIMSs with central angle of 120.

The EA performance is changed by the buckling topology.With the increase of the central angle,the IPF and the ECD of the BIMS continues to decrease.The IPF of the BIMS is greatly reduced from 42.66 kN to 8.52 kN,a decrease of 80.03 %.In terms of the MCF,it decreases firstly and then increases.The SEA has a little decrease.Most of all,the CFE of the lattice structure is remarkably improved.The CFE is nearly proportional to the central angle,increasing from 0.37 at 0to 2.18 at 120.The CFE is tightly relating to the crushing pattern.Lattice with layer-by-layer crushing mode has CFE smaller than 0.74.Lattice with hybrid crushing mode has CFE from 0.89 to 1.51.The CFE of BIMSs with simultaneous crushing mode is close to or even much larger than 2.0.Greatly reduced IPF,remarkably improved CFE and little changed SEA make the BIMS a perfect energy absorber in some protective structures.

The curved-walled topology endows the BIMS negative Poisson's ratio.In crushing,when the struts contact with each other,the square cells convert to triangular cells,and the Poisson's ratio changes to positive,which is mechanism of the gradual rising loaddisplacement curve and the improved CFE.

Based on the four simplified super folding element (SSFE) and flattening element,a theoretical model to predict the MCF of the BIMS is proposed.The maximum error between the theoretical MCF and the experimental value is 12.11 %.Therefore,the MCF calculated based on the theory of simplified super folding element and flattening element is acceptable.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Supports from National Natural Science Foundation of China(11972184 and U20A20286),China National Key Laboratory Foundation of Science and Technology on Materials under Shock and Impact (6142902200203),Natural Science Foundation of Jiangsu Province of China (BK20201286),and Science and Technology Project of Jiangsu Province of China (BE2020716) are gratefully acknowledged.