Adaptive robust control for triple avoidance -striking -arrival performance of uncertain tank mechanical systems
Zong-fan Wang,Guo-lai Yang,Xiu-ye Wang,Qin-qin Sun,Yu-ze Ma
The School of Mechanical Engineering,Nanjing University of Science and Technology,Jiangsu,People's Republic of China
Keywords:Adaptive robust control Multivariable tank system Uncertainty Constraint following Avoidance -striking -arrival
ABSTRACT This paper puts forward an unprecedented avoidance-striking-arrival problem aiming to address the need for tank's uncertain mechanical systems on the intelligent battlefield.The associated system uncertainties (possibly rapid) are time-varying but bounded (possibly unknown).The goal is to design a controller that enables the tank to aim at and attack the enemy tank while keeping itself (out of the enemy fire zone).The tank maintains this condition until reaching the predefined region.In this paper,an approximate constraint following control method is adopted to solve this problem,and the original constraints are creatively divided into two categories: the avoidance -tracking constraint and the striking -arrival constraint.An adaptive robust control method is proposed and consequently verified through simulation experiments.It is proved that the system fully obeys the avoidance -tracking -constraint and strictly obeys the striking -arrival constraint under the control input τ.Besides,the control of the tank vehicle running system and tank gun bidirectional stabilization system are unified to deal with the control signal delay caused by complex uncertainties on the battlefield.Overall,this paper reduced the delay of signal transmission in the system while solved the avoidance -striking -arrival problem.
1.Introduction
The modern battlefield environment is complex with frequently encounters,and it is essential to destroy the enemy while ensuring self-security during encountering.In this paper,an unprecedented avoidance -striking -arrival problem is solved for the current ground weapons and equipment cluster war.The associated system uncertainties (possibly rapid) are time-varying but bounded(possibly unknown).The system consists of our tank hull,the enemy tank,and our tank gun.The problem is intended to obtain a controller which achieves three performances:avoidance,striking,and arrival.In the avoidance performance,the tank is out of the enemy's effective fire zone;in the arrival performance,the tank can reach a predefined region;and in the striking performance,the enemy tank is targeted by our tank within our effective fire zone.
The tank gun bidirectional stabilization system and the tank vehicle running system were considered two independent systems.When the tank gun bidirectional stabilization system is taken as the control object,the current attitude of the vehicle is often ignored[1-3],and the connection between the hull and the turret is saddle ring[4]which is considered a linear relationship even with ground excitation.When the tank vehicle running system is taken as the control object,the turret is only taken as the load,the longitudinal vibration of the vehicle,and the influence of the saddle ring in parameter passing are ignored [5-7].Therefore,transmitting the parameters increases the nonlinearity when the two systems are independently controlled,which reduces the transmission authenticity and real-time performance and increases the control cost.In this paper,two independent systems are combined and the inter-system nonlinearities are converted to intra-system nonlinearities.The nonlinear problems in the transmission of control parameters are solved,and the fast and true response performance of the weapon system is guaranteed in the intelligent battlefield.
In the vehicle running system,the avoidance problem was generally discussed together with the vehicle collision control[8-10].In the military aspect,it was mainly applied to target interception [11-13].However,the problem of arrival is always ignored.In recent years,some scholars had introduced avoidancearrival control considering the simultaneity of avoidance and arrival problems[14,15].In the tank gun bidirectional stabilization system,the tank is only considered static or in linear motion,which is not in line with reality.Therefore,in this paper,a dynamic model is built by integrating the two systems.The expected muzzle angle is no longer dependent solely on the observed value but can be adjusted in advance according to the position of our tank.Besides,it is necessary to ensure that the enemy is within our effective fire zone during the striking process.Hence,the tank vehicle running control system needs to implement tracking performance except for the avoidance and arrival performance.
In the past decades,increasing attention had been paid to the control of uncertain mechanical systems [16-18],and many methods had been proposed to deal with uncertainty.A tracking control method presented by Udwadia and Kalaba had made major contributions to the control of uncertain mechanical systems[19,20],which is widely used in areas such as satellite formation control,and vehicle intelligent driving control[21,22].A method to deal with the uncertainties of the tank avoidance-striking-arrival problem is presented based on it.Here,the uncertainties are timevarying (possibly rapid) but bounded (possibly unknown).Firstly,the control problem in the system is expressed in the form of the approximate following constraints.The dynamic equations are transformed into a general description of the constrained mechanical system with uncertainties.According to the expected performance,constraint equations and tracking objects β are obtained.An adaptive robust control is used to ensure that β is uniformly bounded and uniformly ultimately bounded.Meanwhile,the adaptive law is expressed in the analytic form of binding force for ensuring that the system strictly obeys the constraints.Finally,the compensation item is introduced to deal with the inevitable uncertainties of the system.It can be expected that the ideal system performance will be replaced by the actual system performance,which will allow certain constraints to violate the threshold,i.e.,the approximately followed constraints will replace the actually followed constraints.
The main contributions of this paper are four aspects:Firstly,the independent tank vehicle running control system and the tank gun bidirectional stabilization control system are unified,the control costs of the system are reduced,and the control precision is improved.Secondly,for an uncertain tank system,the simple avoidance or arrival problem is extended to another more practical avoidance-striking-arrival problem.Therefore,the constraints of uncertain mechanical systems are divided into avoidance constraint,striking constraint,and arrival constraint.Thirdly,an adaptive robust control method is proposed in this paper.A supplementary control item is adopted to overcome the influence of time-varying system uncertainties,and the expected system performances are satisfied simultaneously.Fourthly,the system state is uniformly bounded and ultimately uniformly bounded,ensuring that the system fully obeys the avoidance constraint,striking constraint,and arrival constraint,and the proposed method is comprehensively introduced and demonstrated.
2.Tank system dynamics modeling
2.1.Tank gun bidirectional stabilization system dynamics modeling
The dynamic model of the tank bidirectional stabilization system is shown in Fig.1.It contains two sets of loads:the turret load and the barrel load driven by two motors[23].Let m,R,φbe the mass,radius,and angle of the turret,respectively,and let m,R,φbe the mass,radius,and angle of the barrel.The dynamic equations of the system are derived by the Euler -Lagrange equations.Considering the kinetic energy of the turret and the barrel:

Then,consider the turret to be the zero potential energy plane i.e.,H=0.The potential energy of the barrel is H=(mgRsin φ)/2.The system Lagrange is defined as L=V+V-H-H.Suppose the torques acting on the turret and barrel links are τand τ,respectively.Then,the Euler-Lagrange equations:

Substituting V,V,Hand Hinto the formula,the dynamic equations of the tank bidirectional stabilization system are obtained:
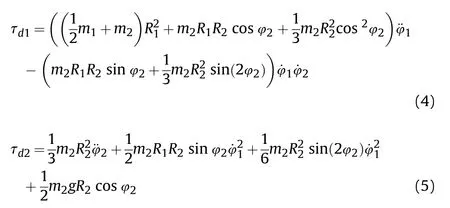
Which can be rewritten in matrix form as:

It is worth noting that m,m,Rand Rare uncertain due to system modeling errors.In addition,the road excitation is not completely measurable.
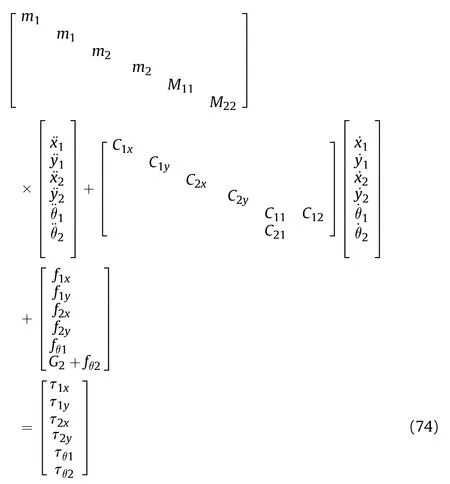
2.2.Tank vehicle running system dynamics modeling
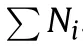
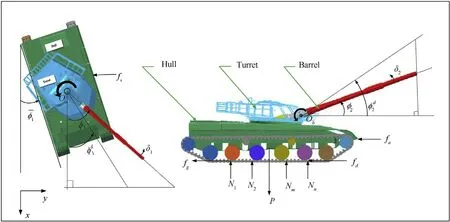
Fig.1.The tank vehicle running system and the tank gun bidirectional stabilization system.
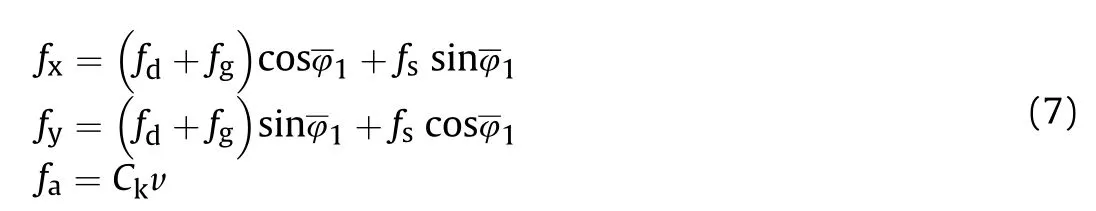
The dynamic equations of the tank vehicle running are represented by

Here the resistances f,f,fand fare all related to the vehicle's gravity P and drag coefficient μ,which are uncertain quantities that fluctuate around the nominal value due to different driving conditions.In addition,since the effective fire zone of the tank is much larger than its turning radius,the coupling problem caused by turning is ignored when calculating the tank dynamic equations.
The tank vehicle system connects with the tank gun bidirectional stabilization system through the saddle ring,a large roller bearing structure for rotating and bracing.Thus it is a highly nonlinear component because of the clearance and elastic deformation.As a result,there are uncontrollable nonlinear factors in the parameter transmission between the two independently controlled systems.Therefore,the saddle nonlinearities were turned into intra-system nonlinearity and solved when the two systems were jointly controlled.
2.3.General description of the constrained mechanical system with uncertainties
The tank vehicle running control system and the tank gun bidirectional stabilization control system can be regarded as a mechanical system with uncertainties (e.g.,road excitation and transmission error).Next,a general form of an n-dimensional controlled mechanical system is considered [25,26].
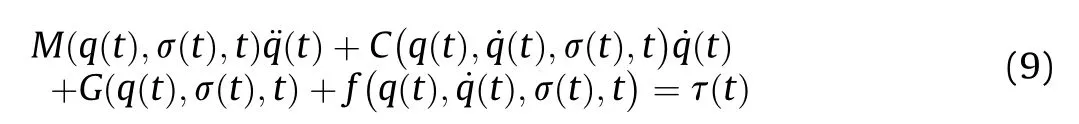
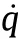
In the following analysis,some parameters in brackets,except for a few critical ones,are omitted for convenience,provided they do not cause confusion.
First,the constraint equations that the system needs to obey are considered,and the first-order form is:


Thus,Eq.(12) can be rewritten as:
3.Constraint -following analysis for the avoidance -striking-arrival problem
3.1.Avoidance -striking -arrival problem statement
In this chapter,the avoidance-striking-arrival problem for an uncertain system is considered as described in the system(1).The constraint-following control is adopted to solve this problem.Therefore,the first problem to solve is constraint -following analysis.The constraints are divided creatively into two categories in this problem:avoidance-tracing constraint and striking-arrival constraint,which are discussed respectively: the avoidance -tracing constraint analysis and the striking -arrival constraint analysis.Firstly,some subsets are defined for later analysis.
System(1)avoids W,if q(t)∉W,then q(t)∉W for all t∊[t,t),where q(·):[t,t)→R
System(1)traces M,if q(t)∊M,then q(t)∊M for all
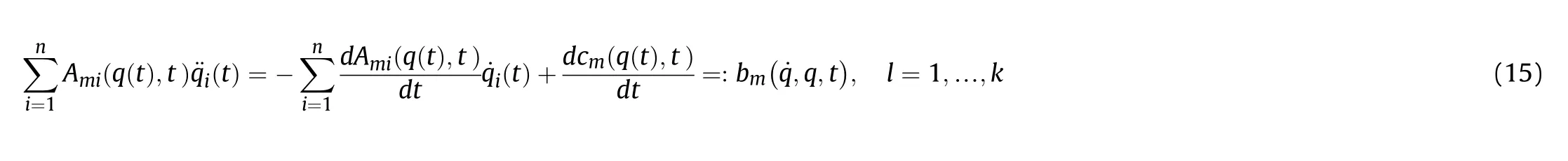
Similarly,let b=[b,b…b],then

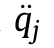
In practical application engineering,the requirements for confinement performance are often not too strict,as long as the constraint conditions strictly follow Eq.(16),which is the difference between engineering constraints and structural constraints (uncertain and unrestricted conditions).In summary,the original constraints can be replaced with the derived constraints when an appropriate control τ is found.This control makes the system strictly obey the constraints of Eq.(16).The constraint following errors are defined as:

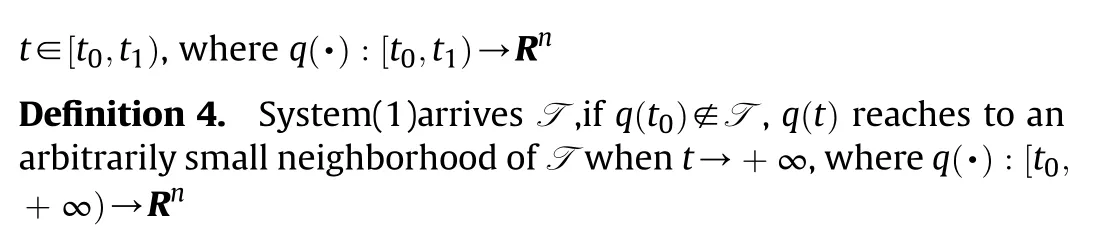
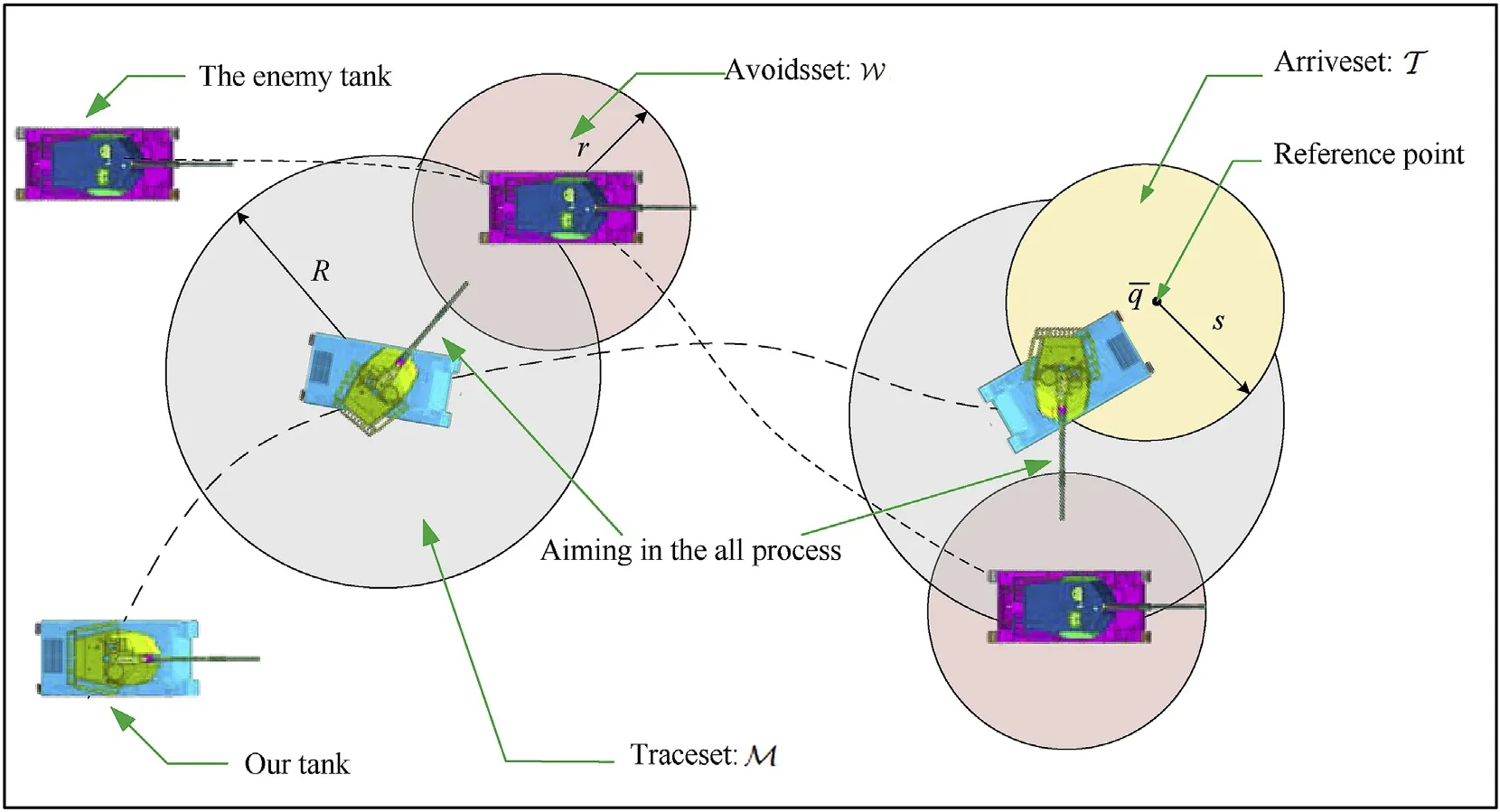
Specifically,the purpose here is to find a controller that keeps the tank out of the enemy's effective fire zone and the enemy tank within our effective fire zone.Moreover,they can reach their respective designated target locations closely while maintaining this relationship.This problem is visually demonstrated in Fig.2:where W ⊂Δ is the avoids set,M ⊂Δ is the traces set,and the arrives set T is a circle of reference point q and radius s.
3.2.The avoidance -tracing constraint analysis


where r,R∊Rare constant,which respectively represent the radius of the effective fire zone of the enemy and our tank.Therefore,to ensure the safety of the tank on the premise of attacking the enemy,the distance between the two is:
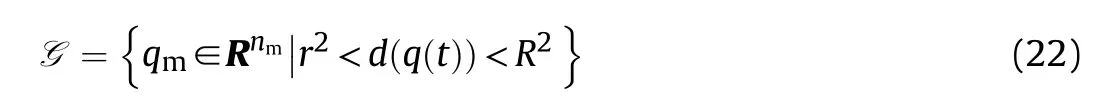
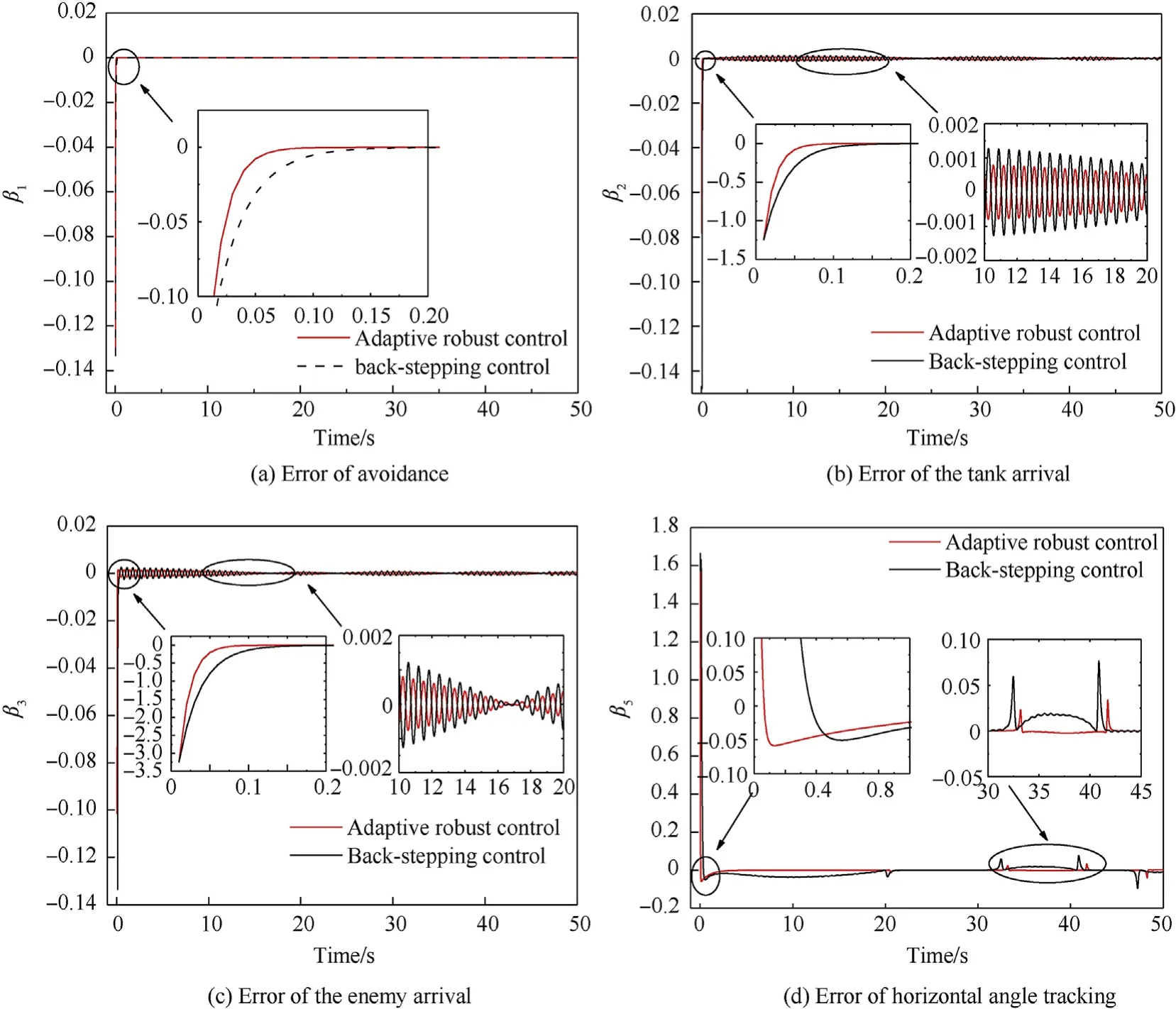
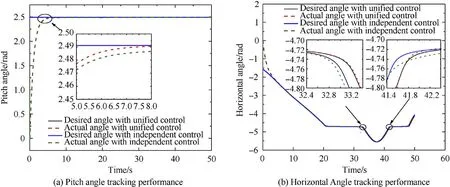
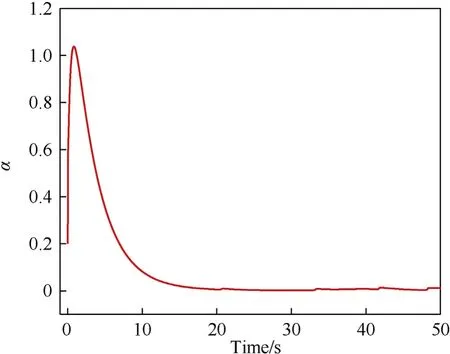
It can be seen that if the tank system is capable of attacking the enemy while protecting itself,a controller is needed that guarantees the distance between the enemy and our tank r The avoidance-tracing constraint system is considered,and the error function is defined as: Taking the first derivative of time: Rewriting it in the first-order form as: and taking the second derivative of time related.Similarly,rewriting it in the second-order form as: Considering the previous definition of constraint -following error(17),there are when r according to the definition of the constraint following errors Eq.(17),assume that the system satisfies Thus,the derived constraint equation and the first and second derivatives are obtained based on the original constraint. The derived constraints are different from the original constraints in expression,but there is a non-negligible relationship between them,i.e.,the derived constraints are derived from the original constraints.Khalil [28,29] proved that,the original constraints could be replaced by derived constraints when a controller is found.The controller makes the derived constraints closely conform to the original constraints. The constraints can be expressed as Eqs.(35) and (36)with different parameter values whether in the tank vehicle running control or in the tank gun bidirectional stabilization control. In this chapter,an adaptive robust control is designed to solve the constraint -following problem of the system,M(∙),C(∙),g(∙)andf(∙)are functions ofq(t),.q(t),σ(t)andt,decomposing them as (Udwadia and Kalaba [30],p.233).Consider the nominal system(41)and the constraint Eq.(16),the constraint force the Lagrange's form of d 'Alembert's principle [31] is considered,and the constraints are satisfied through guiding the system. The Lagrange's form of d 'Alembert's principle guarantees the minimum norm of the constraint force (Eq.(40))and satisfies the Gaussian minimum principle in all the optional forces which conform to Eq.(16) [30]. According to Theorem 2,the system satisfies Eq.(16)by the control inputτ=Τwhen there are no uncertainties in the system.Therefore,these constraints are model-based.However,when there are uncertainties in the system,a transformation is needed if the constraint equation can be continually applied in uncertain mechanical systems. let There is a constant (possibly unknown) η>-1,such that for all(q,t)∊R× R and (iii) non-decreasing with respect to each component of its argumentα. Note that 1+η>0 based on the Assumption η>-1,the vector α may be relevant to the bounding set Σ which is unknown. when only the nominal values are considered in the system,it is easy to obtain that Substituting Eq.(46) and performing it to matrix simplify By Assumption 1 and adopting Rayleigh's principle [32],we have Sorting out Eqs.(58-63),then, Next,by Assumption 2(2),and using Eqs.(48) and (64), Bringing Eq.(50) into the second item of Eq.(55), For the first item of it Khalil and Chen [33,34] had proven that the controlled mechanical system is uniform boundedness by invoking the standard arguments.Let Furthermore,uniform ultimate boundedness also follows with Since constraint βis uniformly bounded and uniformly ultimate bounded by Theorem 3.Therefore,the performance of staying away from the avoidance region and reaching the predetermined region can be achieved when the approximate constraint following control problem is solved. Fig.2.The avoidance -striking -arrival problem for an uncertain tank system. 1) Keep the distance between the enemy and us within our effective fire zone and out of the enemy effective fire zone. 2) The barrel of our tank is always sighting at the enemy tank by adjusting. 3) Maintain relationships (1) and (2) until our tank reaches the predetermined position. The motion equations of the tank are obtained by establishing the coordinate system in Fig.2. Then,the dynamic equations of the tank bidirectional stabilization control system are established through Eq.(6), where mis the mass of the tank,f is external disturbance(possibly from the ground)and τ is the control.Simultaneous Eqs.(72) and (73), The specific meanings and forms have been given above.Next,the constraints of the system will be analyzed from three aspects. Assume that r and R respectively represent the radius of the effective fire zone of the enemy and our tank.According to the expected performance,the distance between the enemy and our tank should be in set S, Then,the derived avoidance-tracing constraint is obtained with Eq.(23) in the first-order form as Taking the second derivative of time where Dis a constant that depends on the external ballistic parameters. Our tank barrel actual angle is [φ,φ],let H(φ,φ)=φ-φ,s=0,writing constraint (37) and (38) in the first-order form and second-order form as where Based on the above results with(77)(78)(80)(81)(82)(83)(85)(86),it is easy to check that where αα>0 are unknown constant parameters.Therefore,Assumption 2 is met by choosing and the adaptive law can be selected according to Eqs.(49) and(50), where kare both scalars. For simulations,the parameters are selected as At the same time,the back-stepping control was selected for the comparative experiment,and the simulation parameters are set as where V,Vare Lyapunov function,β,zare the virtual control objects,and the remaining parameters are the same as above. Fig.3.History of constraint -following error β. Fig.4.Comparison of distance control performance of the enemy and our tank. Fig.5.Tank system trajectories comparison. Fig.6.Comparison of the tank gun angle tracking performance. Fig.7.History of the adaptive parameter . In this paper,the avoidance-strike-arrival problem is proposed for the tank system,which is an uncertainty mechanical system with two sets of control systems.The uncertainties of the system are time-varying (probably rapid) but bounded (probably unknown).A control method is adopted to improve the ability to operate in coordination,formation,encounter combat,and survival.The controller can keep the distance between our tank and the enemy tank within a certain range and adjust the muzzle angle of our tank gun to aim at the enemy tank.Moreover,this relationship can be maintained until our tank reaches the predetermined position or the enemy tank is no longer a threat to our tank.In order to solve this problem,the approximate constraints are used to replace the original constraints,and the control constraints are divided into the avoidance-tracking constraint and the striking -arrival constraint.These constraints include equality constraints and inequality constraints.Then,an adaptive robust controller is designed to ensure that the system can meet two constraints.and the expected performances can be achieved.Comparing with previous studies,the main contributions of this paper are as follows: 1.The tank vehicle running system and the tank gun bidirectional stability system are uniformly controlled for the first time,and the problem of signal transmission delay between the two is solved.The lag of aiming and firing caused by the highly tank vehicle moving has been avoided,and the accuracy of tank gun strikes has been improved. 2.The adaptive robust control method can better adapt to the complex uncertainties of the battlefield and improve control accuracy.Simultaneously,the control object contains multiple degrees of freedom,which is more suitable to the actual situation. 3.This paper provides a theoretical reference for tank control during moving,obstacle avoidance,shooting,arrival,and group combat.Moreover,it avoids self-damage during weapon coordinated combat. This work was partially supported by the Provincial Natural Science Foundation of Jiangsu (Project no.BK20180474),the Natural Science Foundation of China (Project no.51805263,no.51705253,no.11572158). The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.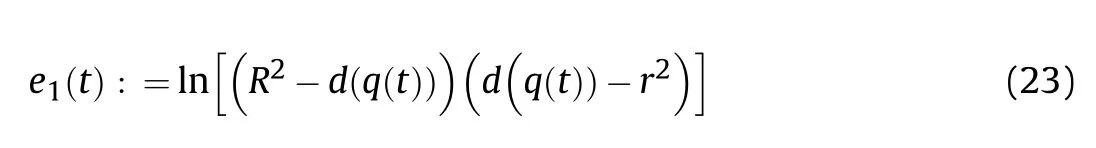
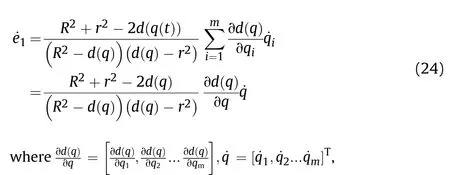

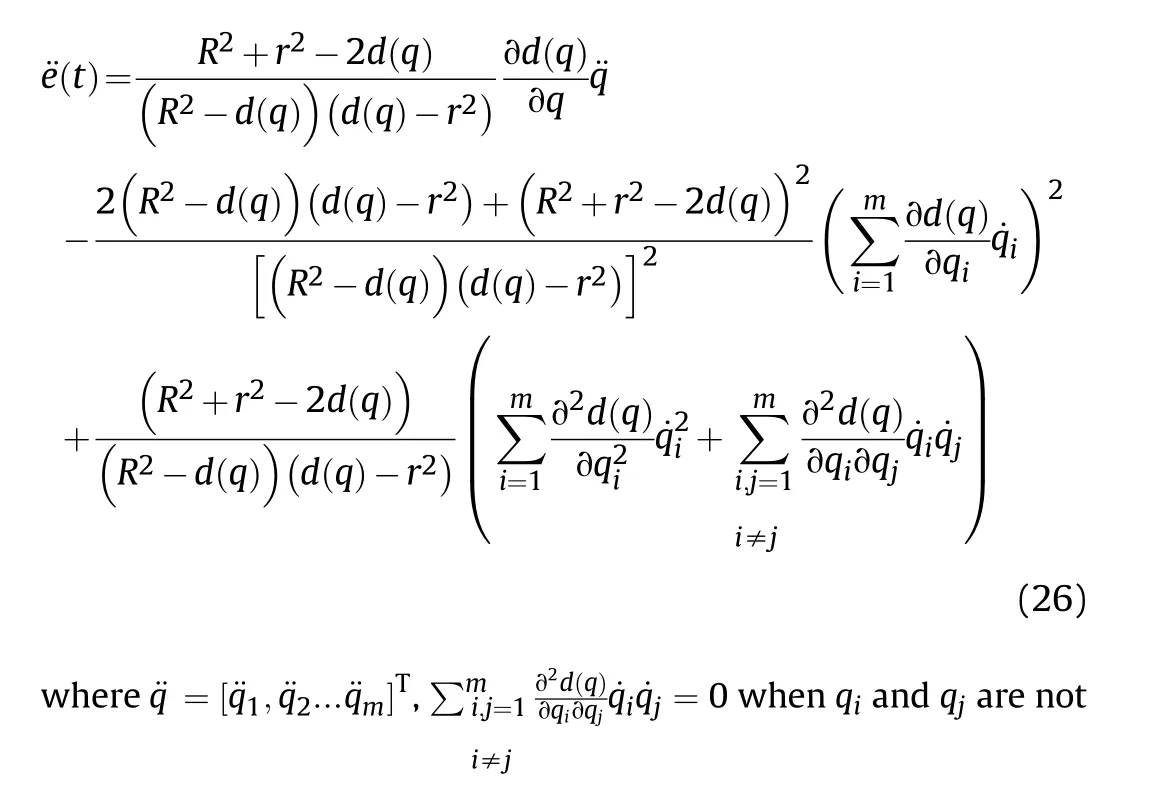



3.3.The striking -arrival constraint analysis



4.Adaptive robust control design


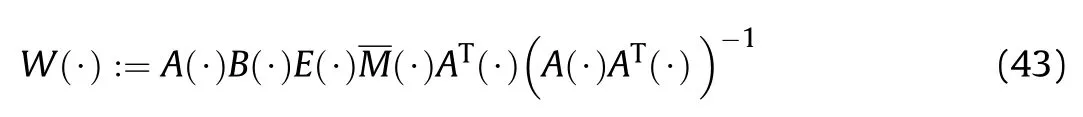

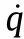

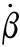

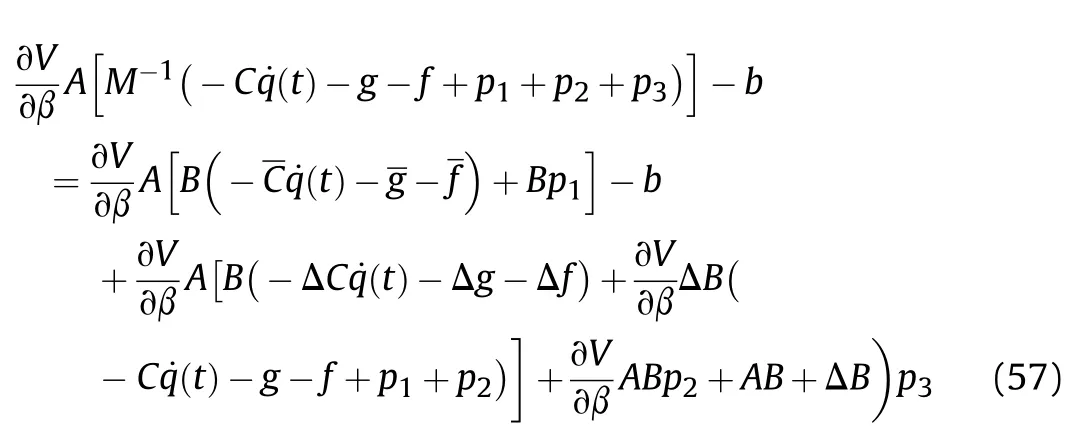
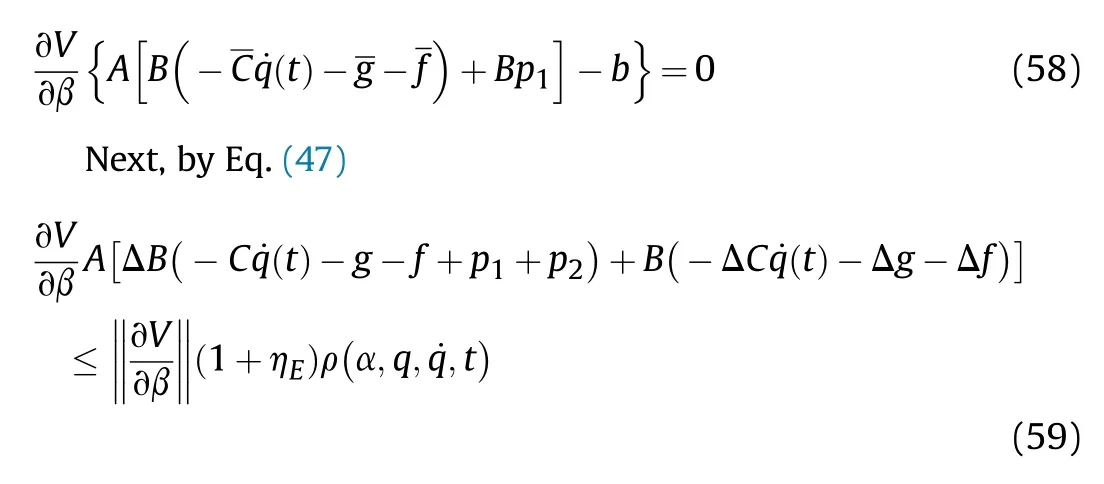

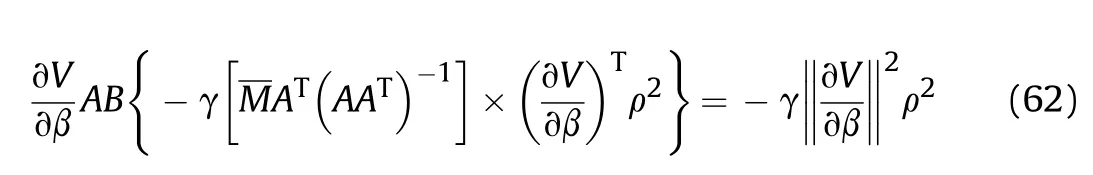
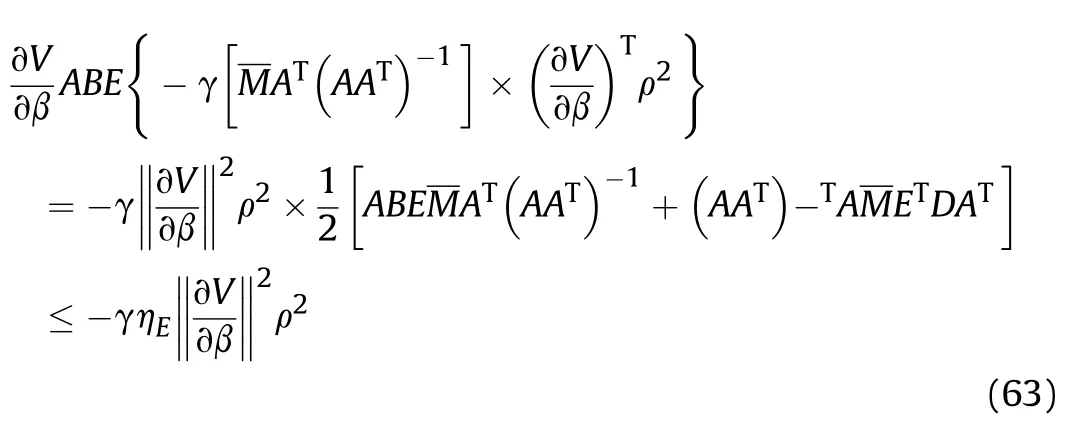

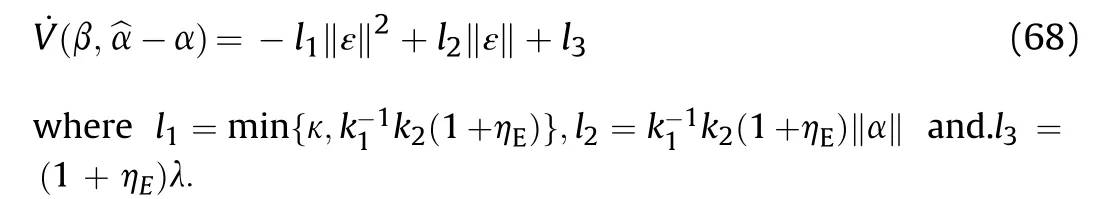

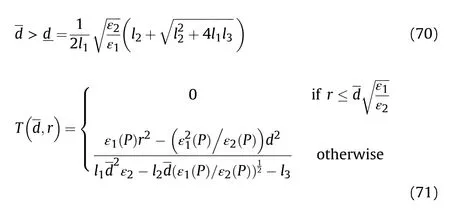
5.Simulations
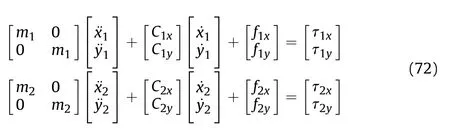
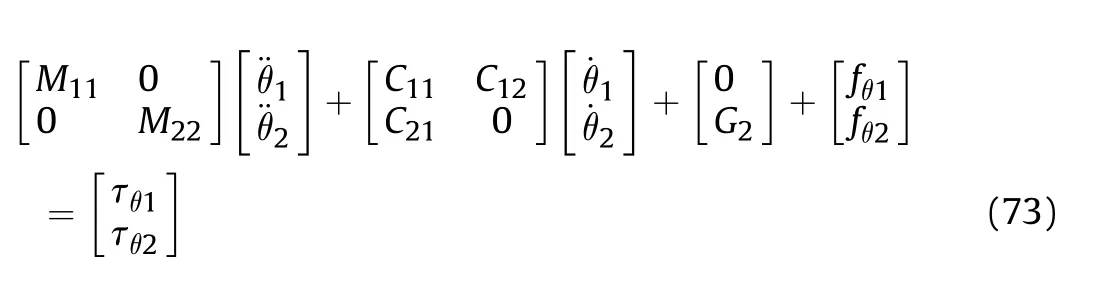
5.1.Constraint of the avoidance -tracing


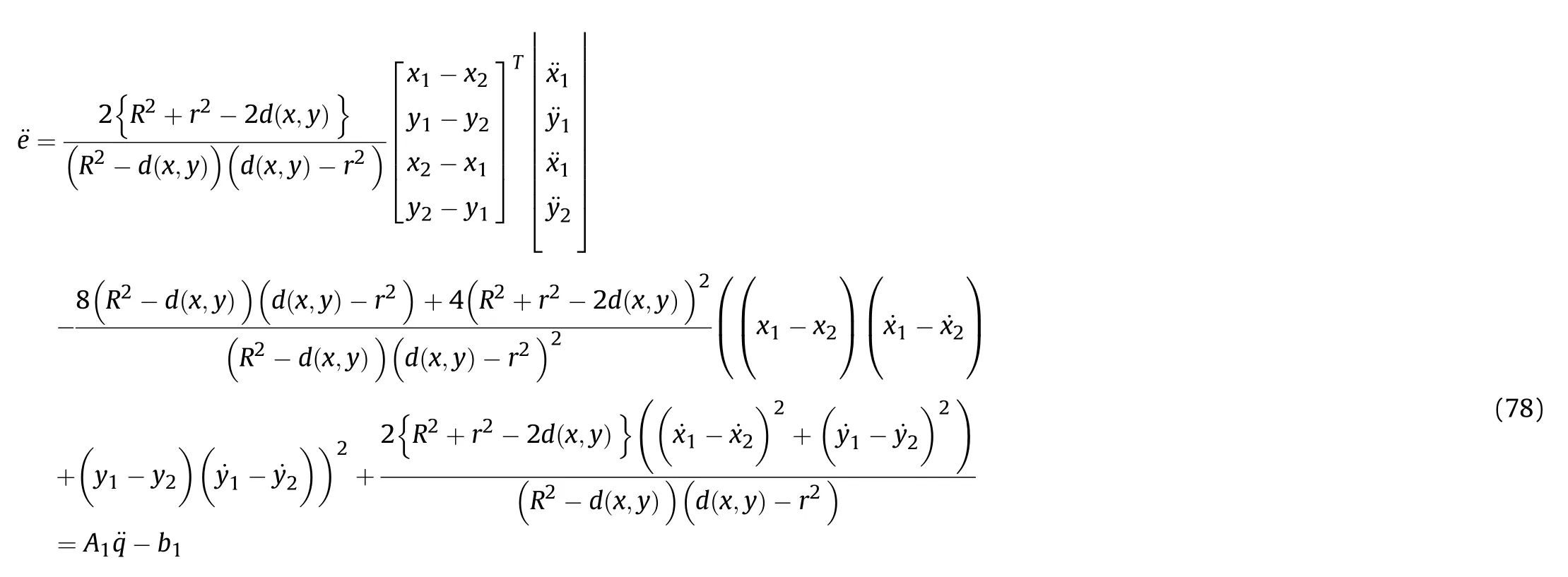
5.2.Constraint of arriving at a predetermined position


5.3.Constraint of bidirectional stabilization control on the tank barrel
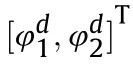
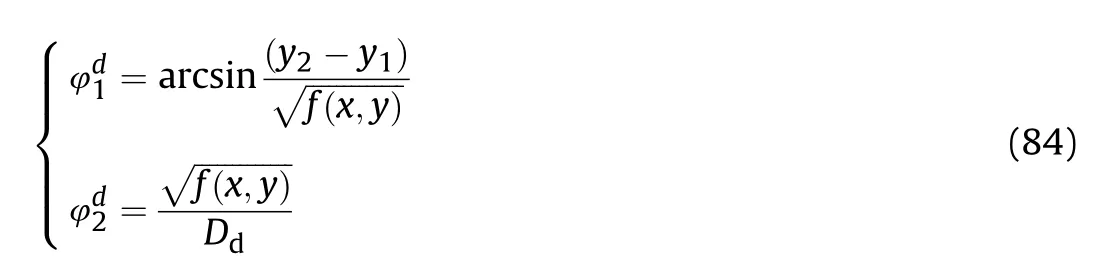
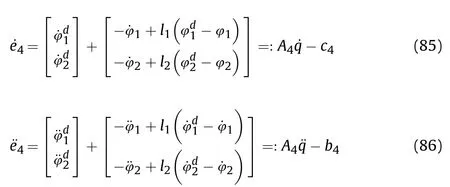
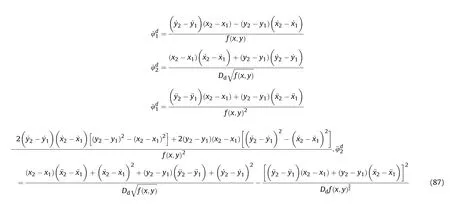
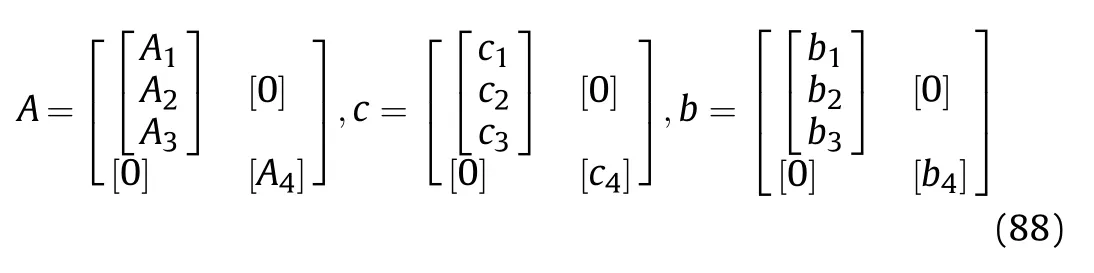

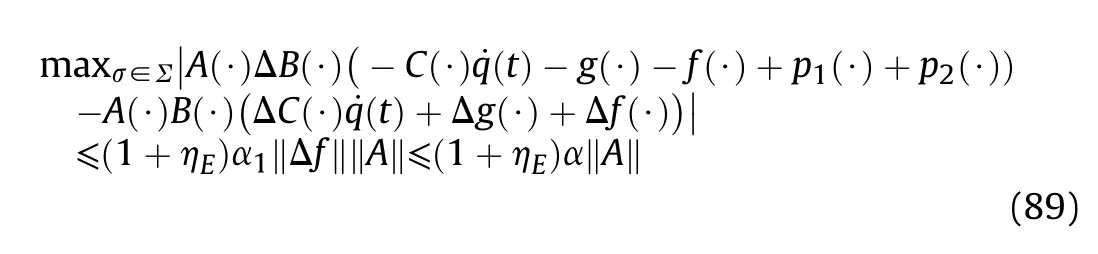

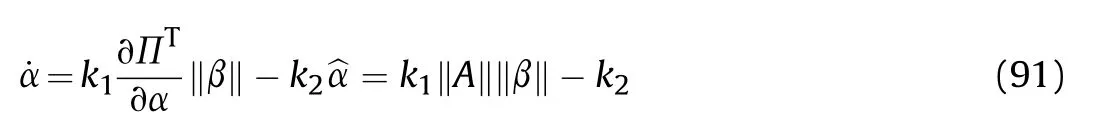





6.Conclusions

