改进麻雀算法优化Elman神经网络的短期电力负荷预测
邹定江, 刘天羽, 王 勉, 段震宇
(上海电机学院 电气学院, 上海 201306)
电力的消耗情况在一定层面上反映了社会的发展现状,由于通过现有手段无法将电能大量储存起来,故对电能进行精准生产和分配就显得尤为重要[1]。短期电力负荷预测是指预测未来几小时、一天或者几天的负荷值,对其进行精准预测可以减少电能及其他资源的浪费[2]。近几十年来,研究者们将智能思想与负荷预测模型相结合[3],如人工神经网络方法[4]、专家系统法[5]、灰色系统法[6]等,旨在提高负荷预测精度。Elman网络属于人工神经网络中的一种,早期被用于解决语音处理问题,后来一些学者将其应用于故障诊断、负荷预测等工程问题[7]。宋明达等[8]将Elman网络用于电力负荷预测,建立了Elman预测模型和BP预测模型,并针对某地区月负荷数据进行了仿真实验,验证了Elman预测模型具有精度高与耗时短的优点。刘远龙等[9]针对Elman神经网络算法容易陷入局部最优以及收敛速度慢等缺点,提出采用粒子群算法(Particle Swarm Optimization,PSO)对Elman网络进行优化并建立了预测模型,经仿真验证该方法能有效克服原模型的缺点。杨芳君等[10]引入随机游动过程与混沌扰动因子的布谷鸟算法(Cuckoo Search,CS),对融合了输入-输出层的Elman神经网络进行优化,并建立了预测模型,通过实例仿真与其他模型的预测结果对比,表明该方法能够减小预测误差。
上述研究均有效提高了电力负荷的预测精度,但是没有解决Elman网络在训练过程中收敛稳定性差的问题。因此,本文针对此缺陷,利用Logistic混沌映射初始化种群并加入随机游走扰动的麻雀搜索算法(Sparrow Search Algorithm,SSA),以优化Elman网络的预测模型。该模型能提高初始解质量及算法搜索能力且具有更优的收敛稳定性,通过实例验证了本文方法的有效性与精确性。
1 SSA
SSA是近两年提出的一种新型群智能优化算法,主要是根据其觅食行为与反捕食行为制定规则,进而构建出数学模型。该算法具有寻优能力强、收敛速度快、参数较少等优点[11]。
1.1 基本原理
麻雀种群分为发现者与跟随者两种类型,并加入了预警机制。觅食规则主要有:①发现者的任务是搜寻拥有大量食物的区域,同时给跟随者提供方向,若麻雀个体适应度值越高,代表其食物资源越多,越容易作为发现者;②种群中一旦有麻雀发现外来入侵威胁,它便会为其他个体传播预警信息,只要预警值超过安全值时,跟随者会跟随发现者前往其他区域觅食;③在能够找到更优食物资源的条件下,跟随者可以成为发现者,发现者也能成为跟随着,但在整个种群中两者各自所占比重不变;④跟随者自身能量越低,其所处位置就越不利,饥饿过度的跟随者会倾向其他区域搜索食物;⑤跟随者始终可以识别出提供最好食物资源的发现者,从该发现者资源里获取食物或从其周围搜索食物,部分跟随者会时刻监视发现者的搜寻状态,然后去争夺食物进而提高自身捕食率;⑥当种群受到外来威胁时,搜索空间外围的个体会立刻往其他安全区域移动,搜索空间内部的个体则会试图靠近其他麻雀[12]。
1.2 数学建模
将麻雀种群用矩阵形式表示为

式中:d为维数;n为种群规模;x nd为第n个麻雀在第d维中的位置。
将种群适应度值用矩阵形式表示为

式中:f为麻雀个体的适应度值。
根据规则①,在种群搜索过程中,食物率先被发现者获得,发现者的位置更新可描述为
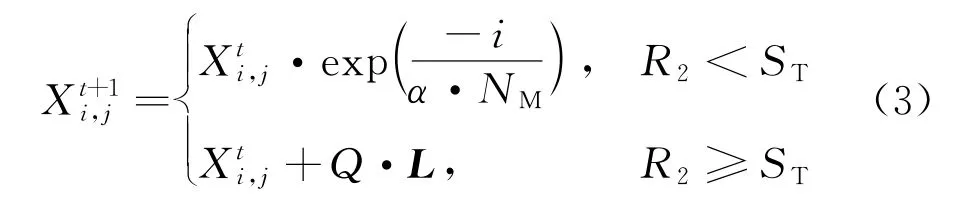
式中:t为当前迭代次数;NM为最大迭代次数;X i,j为第i个麻雀在j维中的位置信息,j为1至d的整数;Q为服从正态分布的随机数;L为单位行向量;α为[0,1]的随机数;R2为预警值,R2∈[0,1];ST为安全值,ST∈[0.5,1]。
根据规则③、④,跟随者位置更新可表示为
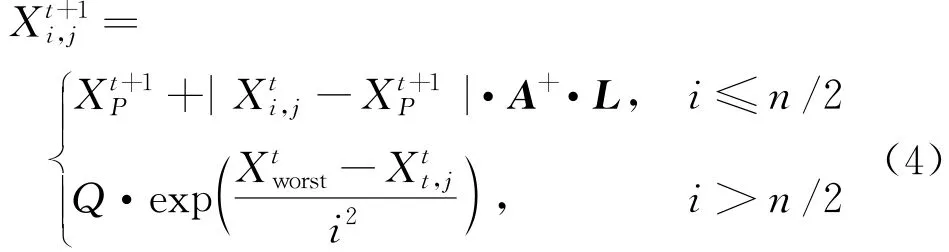
当i>n/2时,表明适应度值较低的第i个跟随者没有觅到食物,需要飞往其他地方觅食。
种群中能感受到外来威胁的个体称为警戒者,占种群数量的10%~20%,其初始位置会随机产生,根据规则⑥可将其位置更新描述为
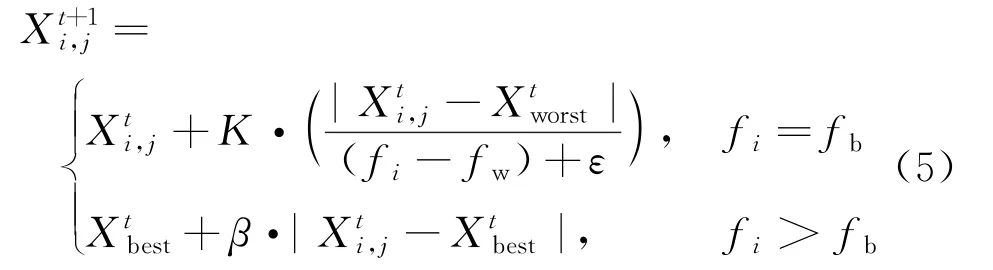
当f i>fb时,搜索空间边缘的个体容易受到外来攻击;当f i=fb时,搜索空间中间的个体也受到了外来威胁,需要向其他个体移动以降低被捕风险。
2 改进麻雀算法
SSA容易在寻优过程中陷入局部最优,可能会获取不到网络最优的参数以致模型的预测精度降低。因此,引入混沌策略提高初始解质量,并利用随机游走策略对最优麻雀进行位置扰动,从而提高局部与全局搜索能力。
2.1 Logistic混沌映射策略
混沌映射常用来生成混沌序列,这是由简单的确定性系统产生的随机性序列,一般混沌序列有非线性、对初值的敏感依赖性、随机性等特征[13]。利用混沌映射对目标进行优化时,可以产生一系列0~1范围内的混沌数。本文将麻雀种群随机初始化,通过Logistic混沌映射的混沌性来替代,可以均匀地使麻雀分布在搜索空间。
Logistic映射的数学表达式为
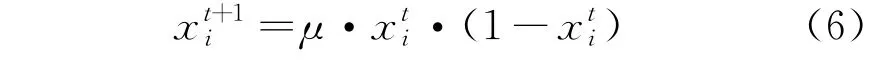
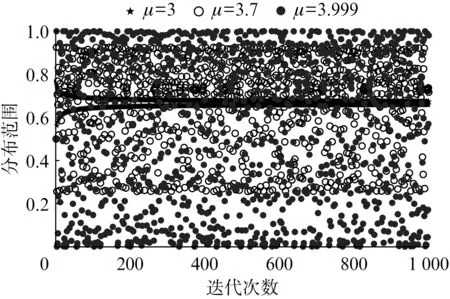
图1 Logistic映射迭代图(x i=0.5)
由图1可见,μ=3.999时,迭代1 000次产生的值均匀分布在0~1之间;μ=3.7时,迭代1 000次产生的值大致均匀分布在0.3~0.9之间;而μ=3时,迭代1 000次产生的值逐渐收敛至0.65附近。因此,在对麻雀种群进行初始化时,让μ值尽量靠近4,这能使麻雀种群均匀散布在搜索空间。
2.2 随机游走策略
随机游走是布朗运动的理想数学状态[14],能使麻雀个体在空间中随机地前进,不局限于某一区域。其形成的算法特点是操作简单且不易陷入局部最优,是一个全局最优化的方法。
最优麻雀随机游走轨迹数组的数学表达式为
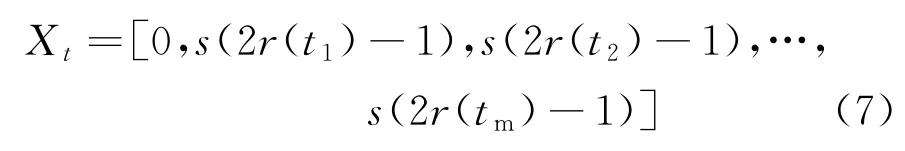
式中:s为计算累加和;t为随机游走步数,即当前迭代次数;tm为最大迭代次数,本文选用NM;r(t)为随机函数,其表达式为
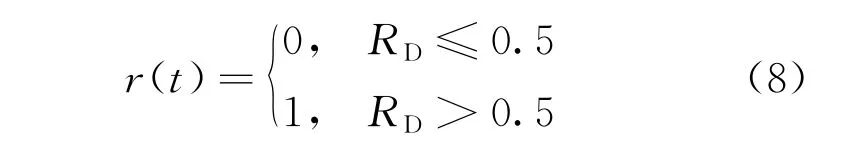
式中:RD为0~1之间的随机数,迭代次数t每增加一次都需重新取值。
为了防止麻雀个体在搜索时越出搜索空间边界,对其进行归一化,其表达式为
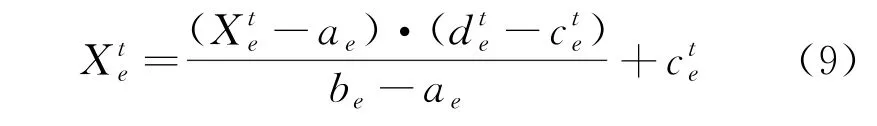
2.3 算法性能分析
改进麻雀搜索算法(Improved Sparrow Search Algorithm,ISSA)寻优过程如下:
(1) 利用Logistic映射策略初始化麻雀种群位置,并确定NM、n、PD、SD、ST参数(PD为发现者比重,SD为警戒者比重)。
(2) 计算麻雀适应度值并进行排序。
(3) 根据式(3)更新发现者的位置。
(4) 根据式(4)、式(5)更新跟随者及警戒者的位置。
(5) 计算麻雀的适应度值并更新麻雀位置。
(6) 根据式(7)、式(9)对最优麻雀位置更新。
(7) 计算麻雀适应度值,更新全局最优位置。
(8) 判断是否满足停止条件。若满足则退出并输出结果;否则重复执行(2)~(7)。
为进一步体现ISSA具有优越性,本文选取了6个经典基准函数见表1。使用SSA、PSO 算法、CS算法与ISSA进行测试并作对比。将所有算法种群规模设置为30,最大迭代次数设置为100次,选用平均值和标准差作为测试评价指标。每个算法独立运行30次,函数测试结果如表2所示,表中加粗数据为各指标最优值。

表1 测试函数
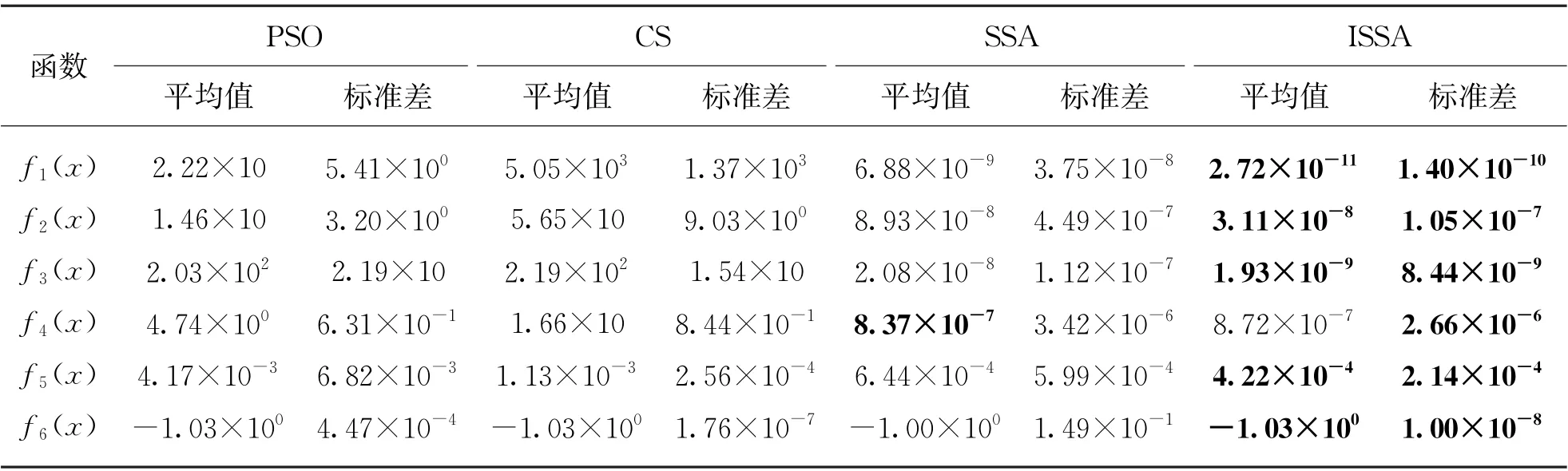
表2 测试结果
由表2可知,对于函数f1(x)、f2(x),ISSA的平均值与标准差远优于PSO、CS,高出SSA 两个数量级;在f3(x)中,ISSA的寻优精度及寻优稳定性远优于PSO及CS,略优于SSA;而在f4(x)中,SSA 与ISSA 寻优精度与稳定性远优于PSO、CS,但SSA的寻优精度略优于ISSA;在f5(x)中,ISSA的寻优精度与稳定性均比其他3种算法强;在f6(x)中,4种算法的寻优精度相差不大,但寻优稳定性远强于其他3种算法。综上所述,ISSA对本文6个函数的寻优性能均有不同程度的提升,并表现出稳定性更好、鲁棒性更强的优势,证明了ISSA的优越性与可行性。
3 ISSA-Elman预测模型
Elman递归神经网络由输入层、隐含层、承接层以及输出层4部分构成[15],如图2所示。图中,w1、w2、w3分别为输入层到隐含层、隐含层到输出层、承接层到隐含层的连接权值;u(k)为输入;x(k)为隐含层节点向量;xc(k)为反馈状态向量;y(k)为输出。
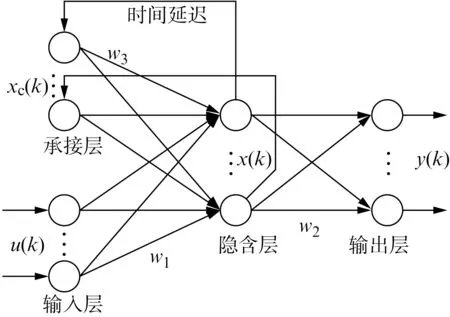
图2 Elman神经网络结构
Elman网络的非线性状态空间表达式如下:
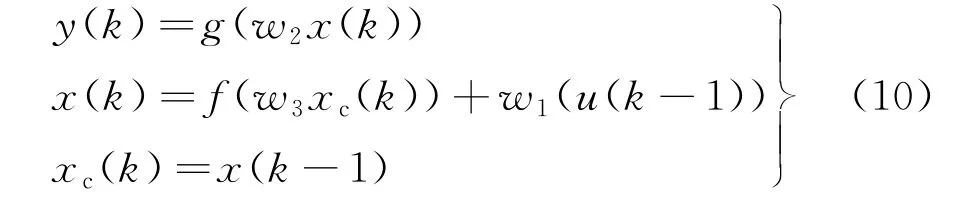
式中:g(·)为输出神经元的传递函数;f(·)为隐含层神经元的传递函数。
采用ISSA优化Elman神经网络算法的建模步骤如下:
步骤1输入数据并进行预处理。
步骤2确定Elman网络的拓扑结构并初始化网络权值与阈值。
步骤3利用Logistic映射策略初始化麻雀种群位置,并设定算法参数。
步骤4计算麻雀适应度值并进行排序。
步骤5麻雀种群进行觅食与反捕食行为并更新个体位置。
步骤6对最优麻雀进行随机扰动,计算麻雀个体的适应度值并更新麻雀位置。
步骤7判断是否满足停止条件。若满足则退出并输出最优参数;否则执行步骤4至步骤6。
4 实例仿真
4.1 选取数据
本文使用某地区公开电力数据集中1月5日~2月5日和5月5日~6月5日两个时间段内,以小时为采样点的1 536组数据作为训练样本,分别对2月6日以及6月6日24个整点时刻的负荷,共48个测试样本进行仿真预测。
电力负荷数据集中,温度、负荷等数据间的量纲不同,需要归一化处理,公式如下:
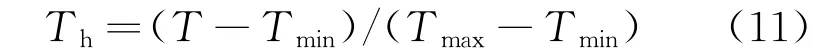
式中:T、Th分别为归一化前后的数据;Tmax、Tmin为归一化前数据集中最大、最小值。
4.2 仿真分析
为了验证ISSA-Elman的精确性,与Elman、PSO-Elman、CS-Elman、SSA-Elman 模型的预测结果进行比较。将历史负荷、温度、日类型等变量作为模型的输入,某一时刻的负荷值作为输出,设置所有种群规模n为10,最大进化代数NM为30,Elman网络最大训练次数为1 000次,学习速率为0.01,训练目标最小误差为1.0×10-6。PSO 加速因子c1、c2均为2,惯性权重w为0.9;布谷鸟种群发现外来鸟蛋概率p a设置为25;SSA 与ISSA 的ST为0.6,PD为0.7,SD为0.2。
图3为算法进化曲线。2月6日,PSO、CS、SSA及ISSA分别在第4、17、22、5次达到收敛,但ISSA的收敛精度相对更高;6月6日,PSO及SSA都在迭代20次时达到收敛状态,CS在迭代27次时达到收敛状态,而ISSA 在迭代至第3次时就已经达到收敛状态,且两天中ISSA 的收敛精度相比另外3种算法更高,可见ISSA 同时保证了适应度与收敛速度,进而提高了算法寻优效率。
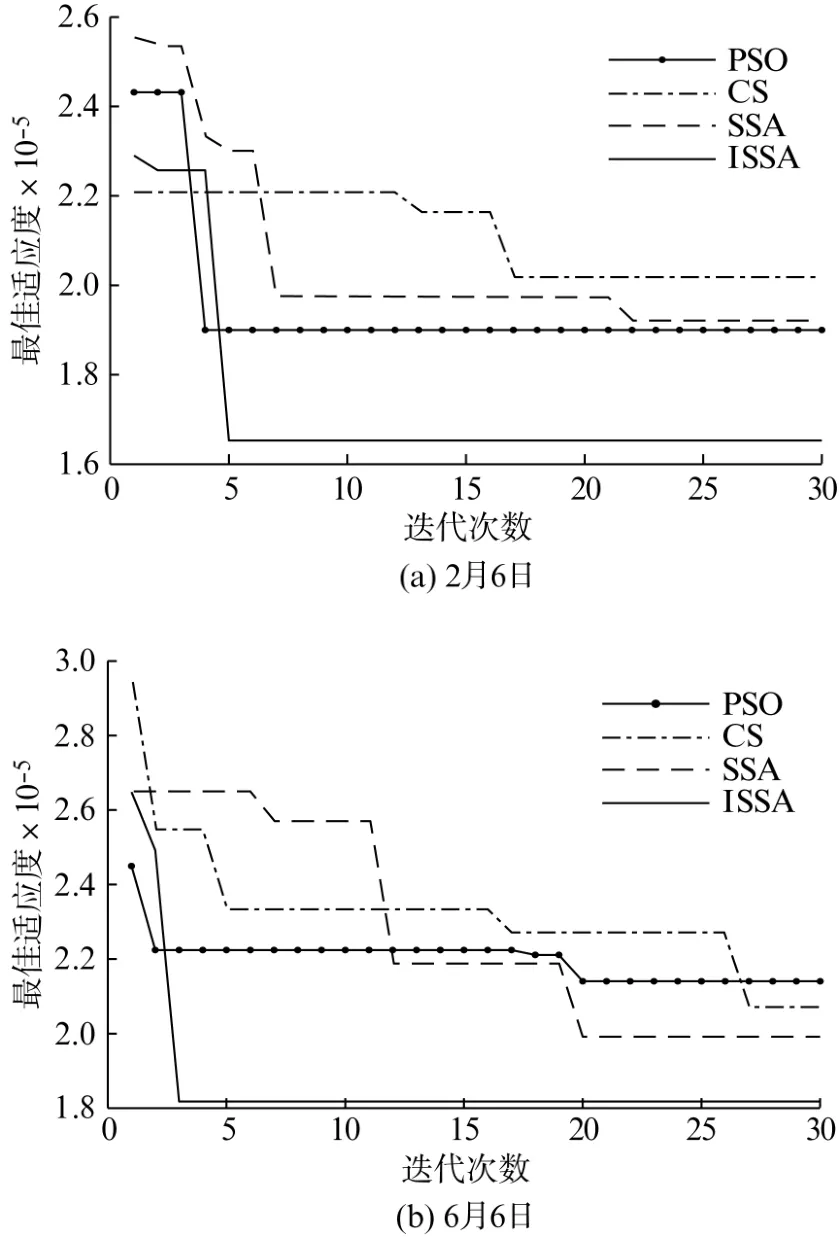
图3 进化曲线
图4为不同模型的预测对比图。ISSA-Elman相比Elman、PSO-Elman、CS-Elman、SSA-Elman模型,其预测曲线与真实曲线拟合度更高。图5为不同模型预测的相对误差曲线,ISSA 模型在两天中的预测相对误差大部分在2%以下,均仅有一个值超过3%,最低分别达到了0.01%及0.22%,且相对误差曲线更平稳,误差值更小。
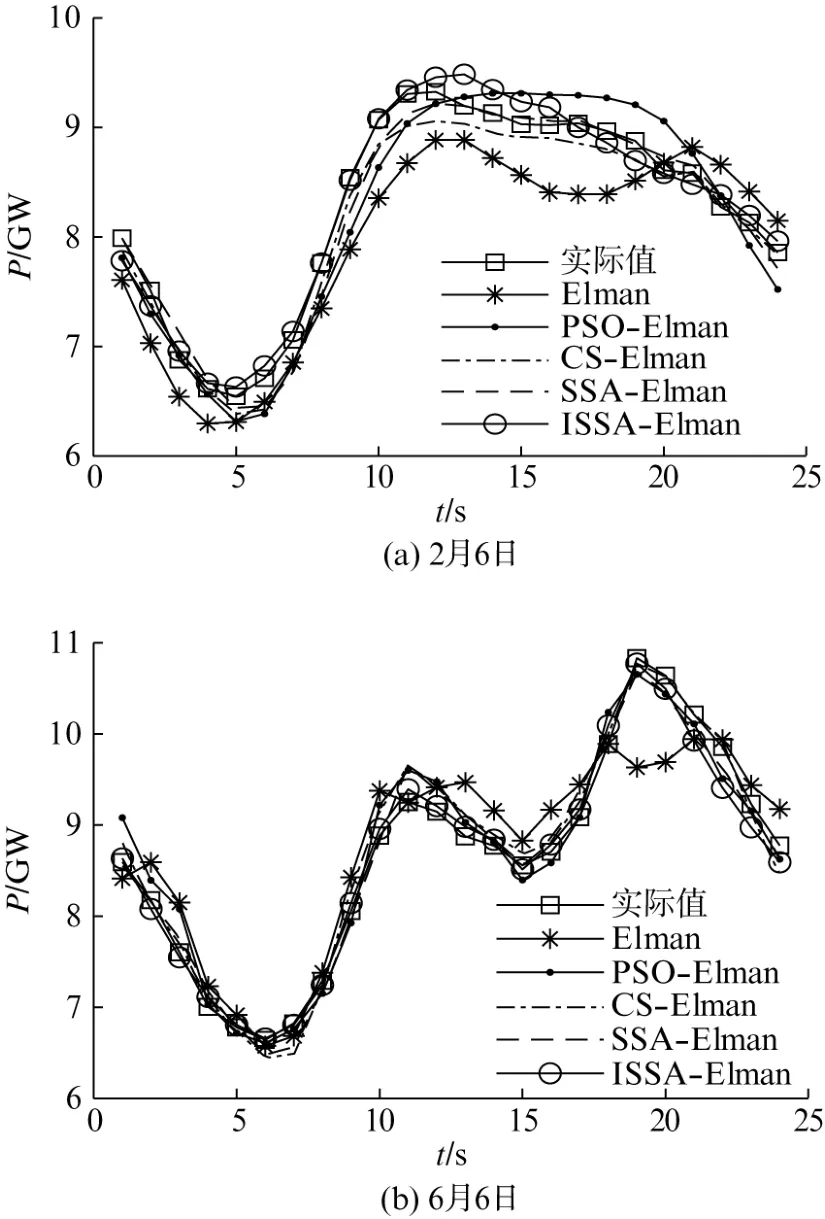
图4 不同模型的预测对比图
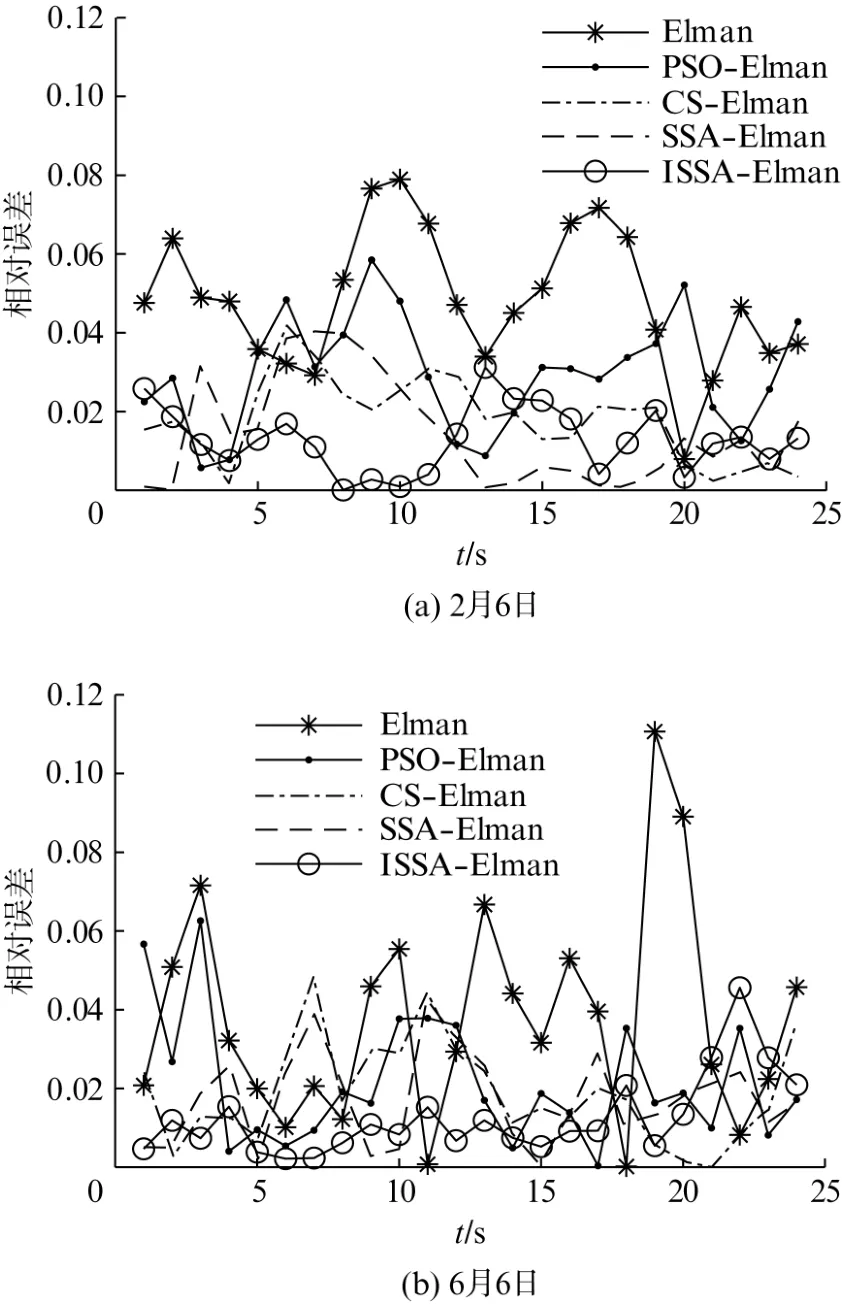
图5 不同模型预测的相对误差曲线
为了进一步体现ISSA-Elman预测模型在实际应用中的优越性,本文通过平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)对模型预测效果进行性能评价,如表3所示,其值越低,表明该模型相对更优,此时负荷预测值与实际负荷值更加接近。
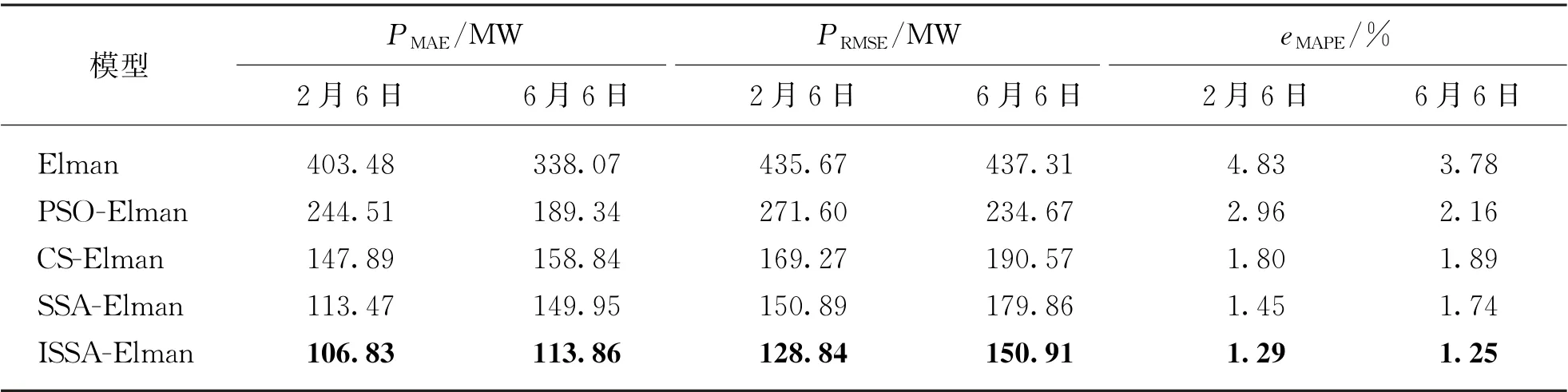
表3 性能对比
由表3可见,两天中ISSA-Elman预测模型的3个指标值均为最低值,对于2月6日,相对其他4种模型的MAE 分别降低了73.52%、56.31%、27.76%、5.85%,RMSE降低了70.43%、52.56%、23.88%、14.61%,MAPE降低了73.29%、56.42%、28.33%、11.03%;对于6月6日,MAE分别降低了66.32%、39.86%、28.32%、24.07%,RMSE降低了65.49%、35.69%、20.81%、16.1%,MAPE降低了66.93%、42.13%、33.86%、28.16%,说明了本文预测模型性能更优。
综上所述,本文提出的ISSA-Elman预测方法提高了对短期电力负荷的预测精度,克服了Elman模型易陷入局部最优的缺点,增强了预测模型的稳定性,针对实际电力负荷体现出了优良的预测效果。
5 结 语
本文提出了一种基于改进SSA 优化Elman神经网络的短期负荷预测方法,该方法根据Logistic映射的混沌性原理对麻雀种群进行了初始化,提高了初始解质量;在种群搜索后,利用随机游走对最优位置的麻雀进行扰动,从而对Elman神经网络进行优化并应用于短期负荷预测中。经实例仿真,ISSA 对Elman网络进行优化后,能够增强收敛稳定性,同时将预测的相对误差值稳定在1.5%以下,有效提高了电力负荷预测精度,对实际工程应用具有重要意义。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

