基于负载观测器的永磁同步电动机自抗扰控制研究
王卓用, 姚晓东
(上海电机学院 电气学院, 上海 201306)
新能源电动汽车驱动系统的核心是电机控制技术,而永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)作为汽车驱动系统主要的受控对象,在应对复杂的路面情况时负载会发生突变,以传统PID调速控制方式易于实现,但是无法高效地满足驱动系统的动态性能和抗干扰的要求[1-2],需要进一步提升电机调速性能和抗干扰能力[3]。现代电机控制理论发展至今,由单一的方式变得更加多元,例如自抗扰控制在速度环中的应用[4]、滑模变结构控制在观测器和速度控制器中的应用[5]、模糊神经网络[6]、模型预测[7]和线性自抗扰[8]等控制方式。虽然在模糊神经网络控制下具有解决快速性和超调量的能力,但是模糊规则的选取,神经网络的结构优化问题还有待解决;滑模变结构能够提高系统稳定性,但不能克服滑模结构自身存在的抖动缺陷[9];模型预测虽然有不错的稳态和动态性能,但目前存在运算量较大的问题[10];线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC)具有较低的运算量、较少的调参量和良好的鲁棒性的优点,但是在负载干扰时存在系统调节时间相对较长的问题;自抗扰控制(Active Disturbance Rejection Control,ADRC)技术是针对传统PID存在诸多问题而设计出的解决方法,其可以不依赖于精确的数学模型,对非线性系统有良好的控制性能[11]。为了进一步提高系统的鲁棒性,有学者采用观测器将负载转矩变化用于前馈补偿,通过控制器减小扰动,而降维负载观测器[12]以其结构简单、运算量小和辨识精度高被广泛应用。
通过以上分析,本文将采用ADRC技术设计速度环代替传统控制器控制[13],利用降维负载转矩观测器对负载转矩进行观测,并将转矩前馈至速度环控制器中进行校正补偿[14-15]。仿真结果验证了该方法可以有效提高电机抗负载扰动的能力。
1 PMSM 的数学模型
假设PMSM 为理想电机,不计各种损耗和饱和,且电流为三相对称的正弦波。则在d-q同步旋转坐标系下定子电压方程为
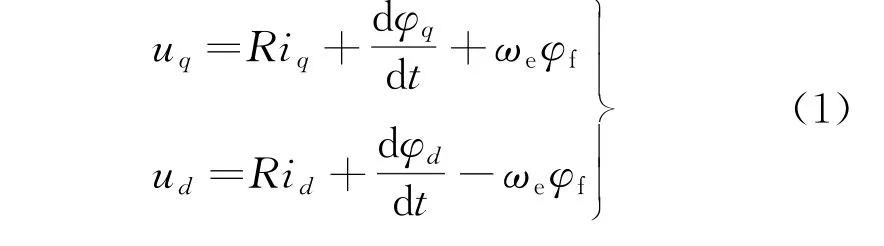
式中:φd、φq为直、交轴磁链;R、ωe为定子电阻、电角速度;u d、u q为直、交轴电压;φf为永磁体磁链;i d、i q为定子直轴、交轴电流。
定子磁链方程为
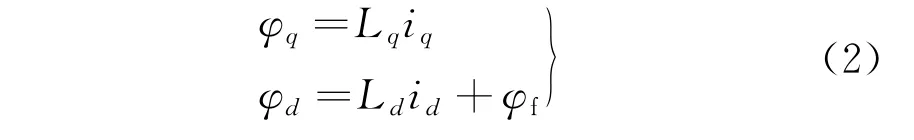
式中:L d、L q为直、交轴电感。
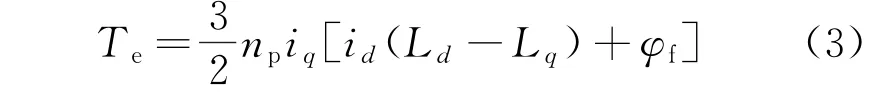
电机机械运动方程为
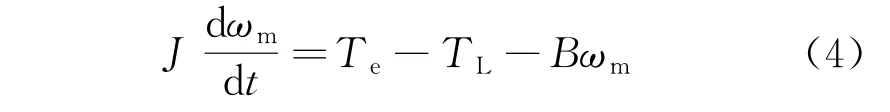
式中:B为摩擦因数;J、TL为转动惯量、负载转矩;ωm为电机机械角速度。
2 速度环自抗扰控制器设计
鉴于电流环的输入信号实时响应的要求,调速系统的电流内环继续由PI控制,而外环速度环则由ADRC 技术结合PMSM 数学模型重新设计。由于ADRC是基于PID控制方法利用控制目标与实际目标之间的误差去消除自身误差,再通过现代控制理论减少PID 闭环系统易产生的超调量,使误差微分的作用充分反馈到系统中,因而具有算法结构简单、各环节参数数量少且调节难度简单、抗干扰能力强等优点。结合以上分析可知典型ADRC是利用跟踪微分环节控制过渡的过程,为非线性环节提供状态参数值和控制参数值,扩展观测器观测负载扰动,最后补偿干扰造成的影响,其结构如图1所示。
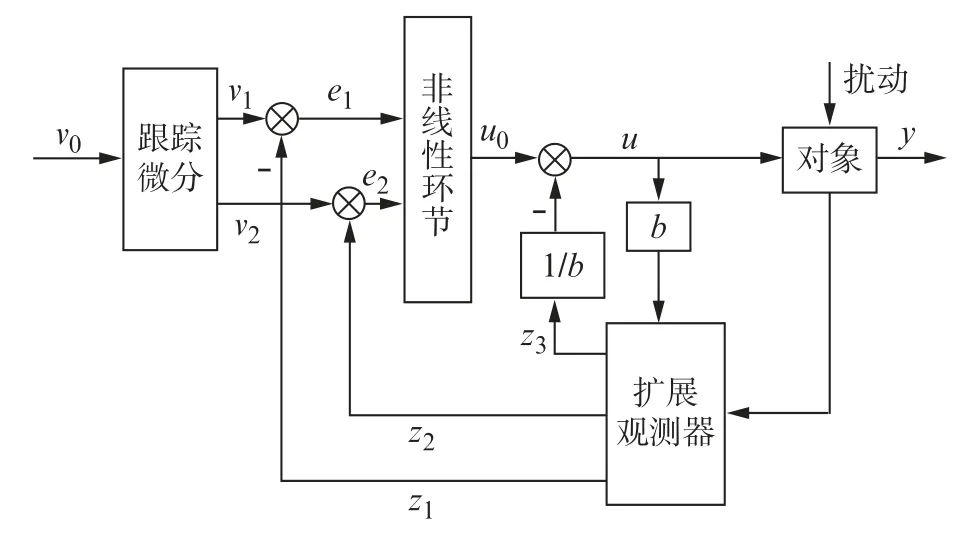
图1 典型ADRC结构
2.1 跟踪微分环节
针对初始状态时,控制量与反馈量之间误差过大会导致控制信号失控,对控制系统产生较大的影响,故利用跟踪微分环节快速跟踪输入转速信号,合理安排一个过渡过程,同步计算出该过程的各阶微分量,即
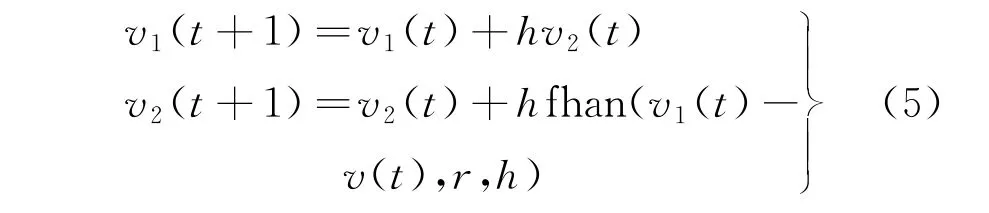
式中:v1(t)为v(t)的跟踪信号值,其中v(t)为输入信号值;v2(t)为v1(t)微分信号值;h为采样因子;r为速度常数;函数fhan为
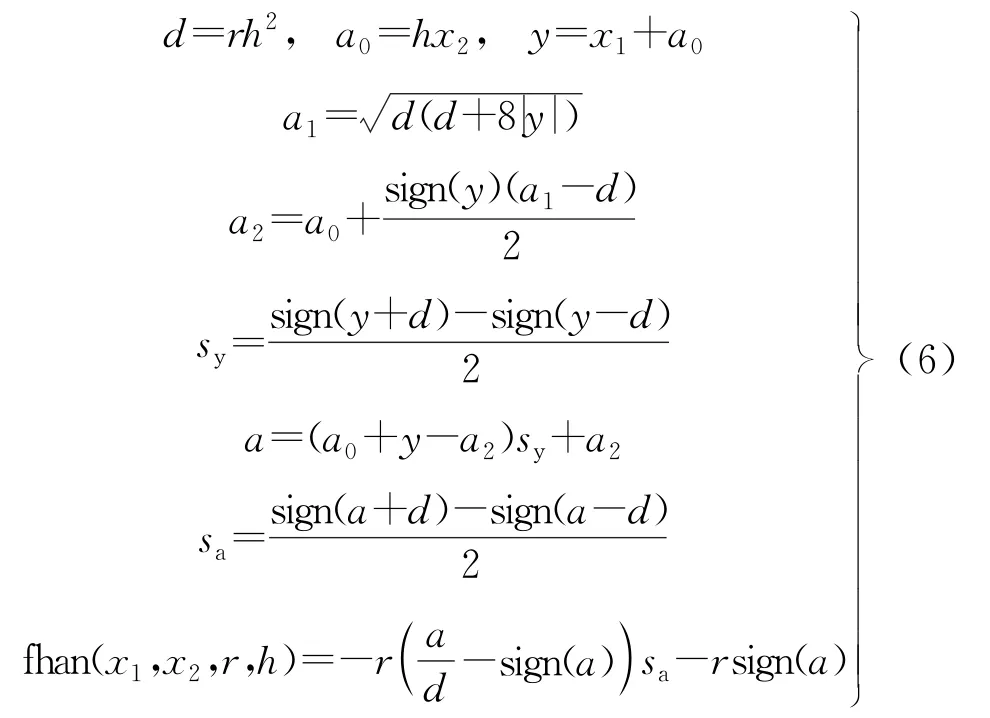
式中:x1、x2为输入量;d、a0、a1、a2为中间量;sy、sa为自定义函数;sign为符号函数。
(3)硅质岩为霏细-粒状结构,层状、块状、蜂窝状构造,金属矿物及其氧化物沿裂隙呈脉状或浸染状分布。硅质岩的成因及沉积环境对成矿作用具有重要意义。
2.2 扩张观测器
通过扩张观测器来观测系统的输出状态量及扰动情况,对输出量进行滤波并消除系统内部各部分增益带来的影响,增强系统的抗噪能力,输出相应的补偿量为
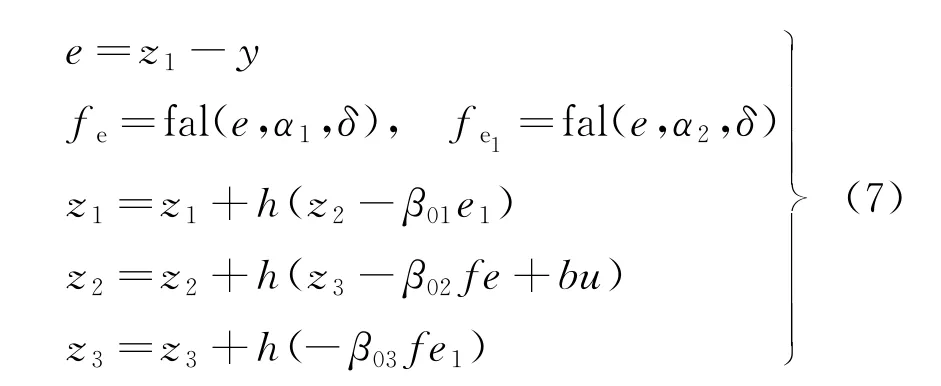
式中:e为内部误差量;z为中间量;β为灵敏度控制量;u为控制指令;b为补偿参数;α为幂次;δ为线性区间;fal函数为
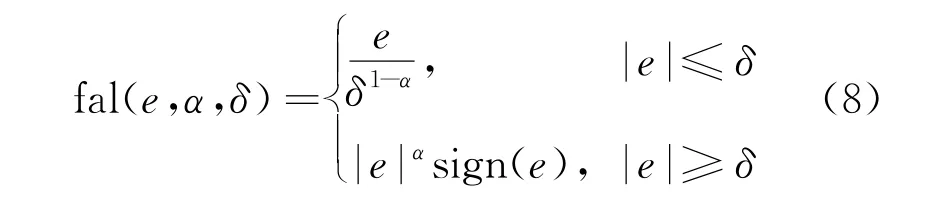
2.3 非线性控制律
非线性控制律主要通过控制参考输入量和误差反馈以抵消扰动量,使误差快速收敛且无高频抖振现象,并经过该环节内部计算可获得被控对象的控制指令,表达式为
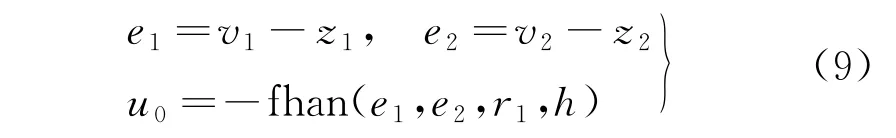
式中:u0为未补偿指令信号;r1为速度常数。
2.4 扰动补偿环节
根据未补偿的控制信号与估计扰动信号,通过线性计算获得补偿信号,表达式为
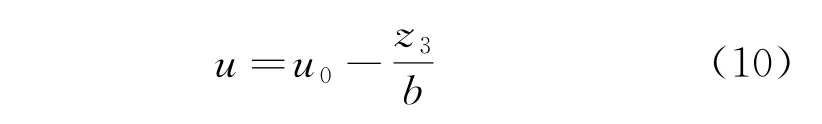
2.5 ADRC参数整定
在跟踪微分环节中需要整定采样因子h和速度常数r。h也为控制器的采样步长,设置过小会加大运算量,对实际影响不大,一般取0.001;r反映了对跟踪目标的响应速度快慢,一般参数设置越大跟踪越快,但会导致超调和噪声含量较大。根据PMSM 自身特性及实践经验,可将r设置为1/h2左右[16]。
扩展观测器涉及参数过多,首先fal函数中幂次α分别设置为0.5、0.25,线性区间δ设置为2.5h,δ值主要反映系统误差范围,过小会导致高频振荡。其中β01一般设置为1/h即可,β02一般设置为1/(2.5h1.25)左右,β03 一般设置为β02 的1~2个数量级即可,参数β主要反映了系统状态误差的反馈增益,取值越大调节速度越快,过高时会导致系统超调且波动较大。b可根据式(12)计算得出[11]。
在非线性控制律中,参数r1取值越大,响应速度越快,过大会导致曲线振荡较大,较小时响应速度变慢,跟踪不上设置目标,一般取值为0.05/h左右[3]。
3 PMSM 控制模型设计
ADRC的控制状态方程标准形式为
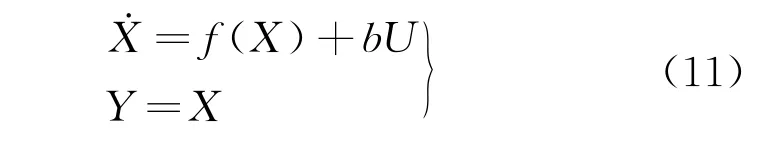
式中:U为输入量;X为中间量;Y为输出量;b为补偿参数。
将PMSM 的数学模型和ADRC相结合,根据式(3)、式(4)可得转速的状态方程,将交轴电流i q设置为转速环的输入变量,状态方程中间变量为转速ωm,则转速环的输出变量为Y,即转速环的状态方程可表示为
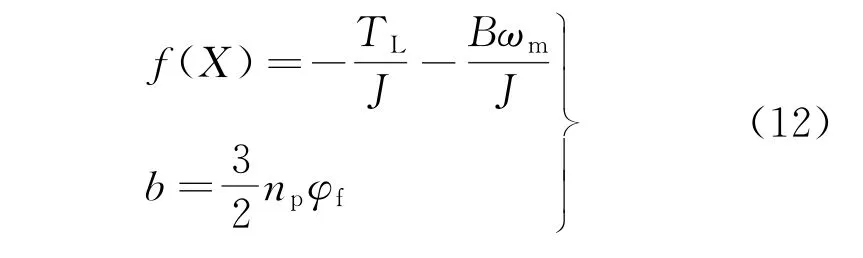
4 负载转矩观测器及前馈补偿设计
4.1 负载转矩观测器
假设采样周期足够小,则可近似认定在一个采样周期内TL是一个恒值[17],即

根据式(4)、式(13)对状态量x=[ωTL]设计负载降维观测器:
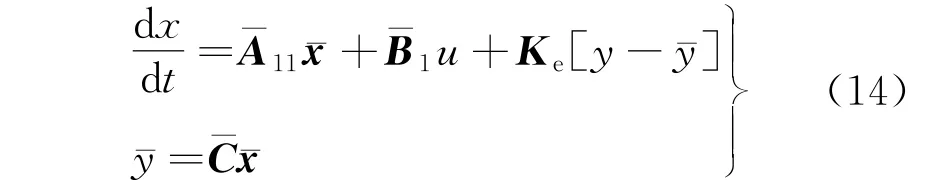
式中:
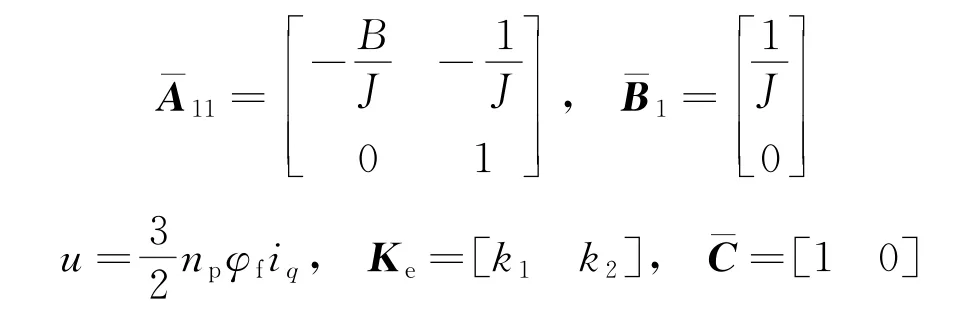
则其特征方程为
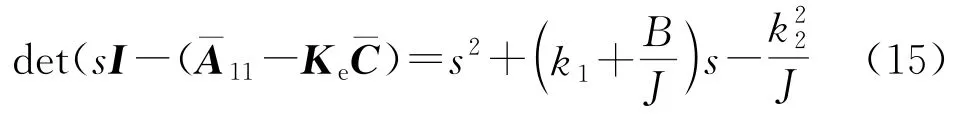
式中:s为复参变量;I为单位矩阵;Ke为反馈增益矩阵;k1、k2分别为反馈增益值。
由极点配置方法配置负载观测器的增益Ke,假设期望极点是α、β,则期望的特征根多项式为
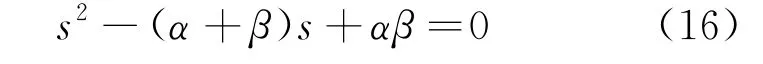
假设B=0,根据式(15)、式(16)配置期望特征根方程,即可得
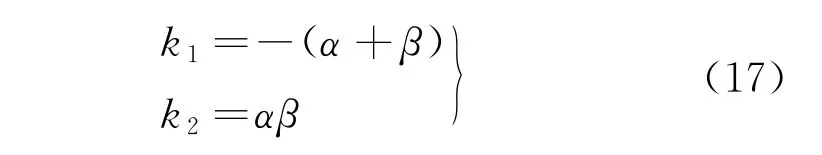
根据式(14)简化得
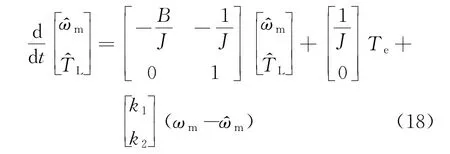
根据式(18)构建降维负载观测器,其结构如图2所示。
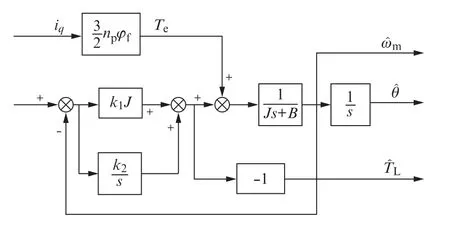
图2 降维负载观测器结构
4.2 转矩前馈补偿
将负载观测器观测到的负载转矩信号,按照一定比例前馈补偿[18]到ADRC控制器输出的转矩电流中,其中负载转矩的补偿系数为Kt=1.5npφf。
5 仿真与实验验证
为检验该模型的自抗扰特性,在Matlab平台上设计了PMSM-ADRC 模型。该控制模型的电流环由于要求输入电流值,实时性较高而继续由PI控制,速度环则根据ADRC技术结合PMSM 数学模型重新设计,以及负载观测器将转矩电流前馈的补偿环节,与传统PI控制、LADRC系统在仿真平台上进行仿真比较。PMSM 和ADRC 参数如表1、表2所示。
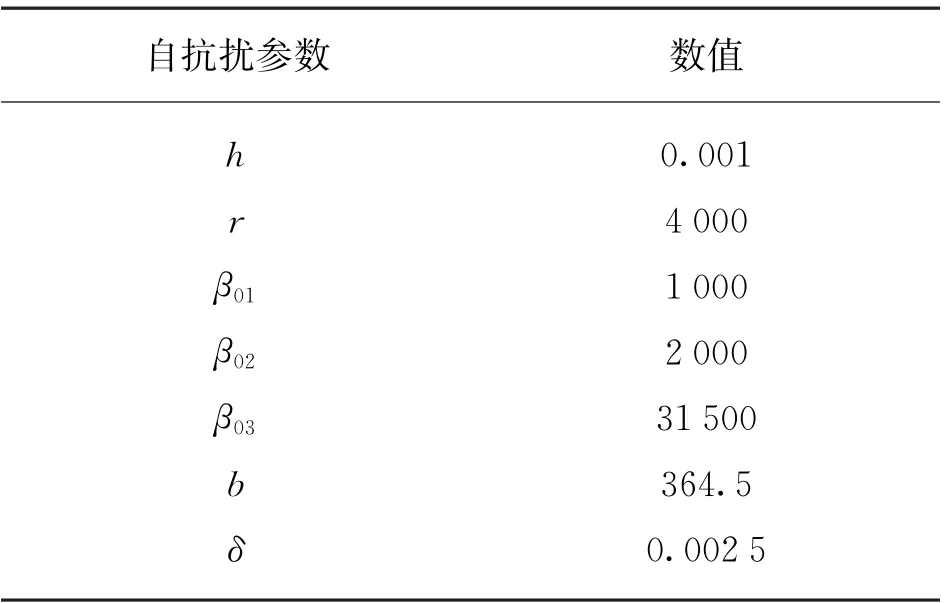
表1 ADRC参数
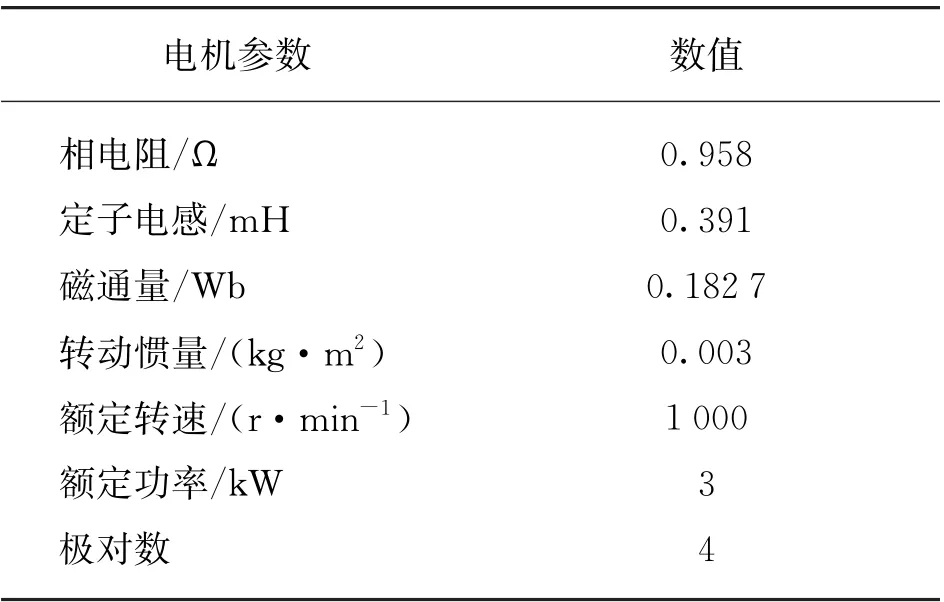
表2 PMSM 参数
5.1 负载转矩跟踪分析
图3为负载转矩跟踪波形图,可知PMSM 在零时刻处于零转矩负载启动,在0.15 s时刻负载转矩为8 N·m 并持续了0.1 s,在0.25 s时负载转矩下降为6 N·m 并持续到结束。从收敛速度上来看,在0.155 s时转矩观测值就跟踪上控制目标转矩,在0.178 s时就使观测曲线与实际曲线重合且振荡趋于稳定,而且转矩超调量为50 mN·m,之后的稳态误差均不超过10 mN·m。在实际转矩下降为6 N·m 时,负载转矩观测器的动态响应时间仅为80 ms,转矩超调量仅为45 m N·m,稳定误差为11 mN·m。由此可见,观测器在任何时刻应对负载突然改变时,对实际目标能做出快速反应并准确地追踪,而且观测精度较高。
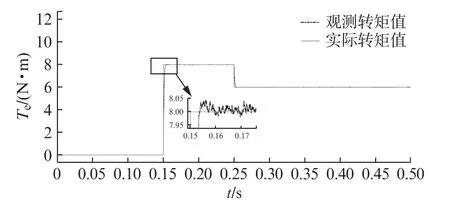
图3 负载转矩跟踪波形
5.2 ADRC调速分析
在初始条件下PMSM 在零负载启动时将转速预设置为1 000 r/min。在启动后0.2 s突加负载8 N·m 和0.3 s突减负载4 N·m 进行测试。PI控制、LADRC控制以及带有转矩前馈的ADRC调速曲线如图4所示。电机在零负载启动时,自抗扰控制能够快速达到预定转速值,从细节图中可以发现自抗扰控制器可以实现几乎为零的超调量。
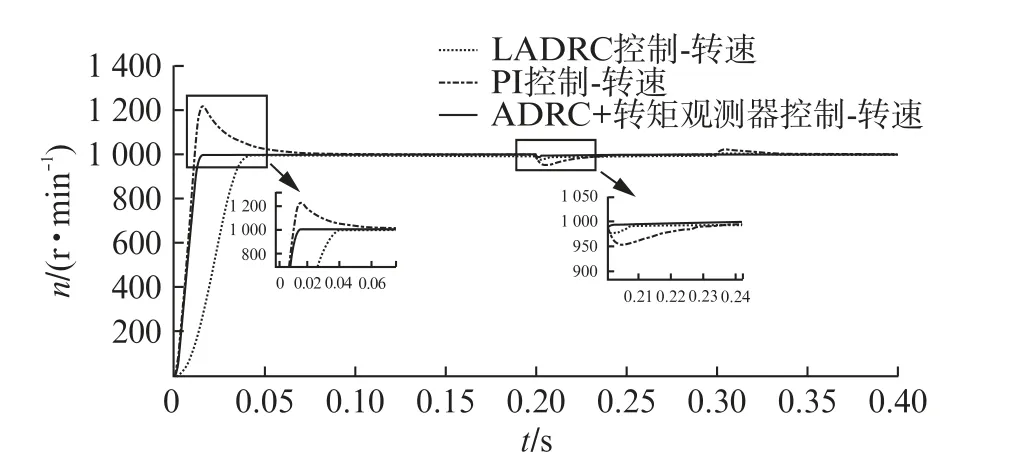
图4 PI、LADRC和ADRC调速曲线
由图4可知,PI控制在达到调速目标时产生了较大的超调量,且曲线波动较大。从局部细节可以看到,在达到给定转速时PI的超调量为20%且达到稳定转速需要60 ms;LADRC控制几乎无超调,但是响应速度较慢且达到稳定转速需要时间为40 ms;带有转矩前馈的ADRC的超调量几乎为零且达到目标转速的时间比PI快了近50 ms,相较于LADRC快了近30 ms;在0.2 s时负载转矩为8 N·m,PI响应时间较长且超调量为0.9%;LADRC的超调量为0.15%之后很快趋于平稳;带有转矩前馈的ADRC转速曲线几乎无变化;在转矩突降4 N·m 时,PI控制调速系统响应时间长而且曲线毛刺较多,超调均差远大于带有转矩前馈的ADRC控制和LADRC控制,恢复到目标转速所需时间较长,而且带有转矩前馈的ADRC控制的转速曲线几乎无波动。
图5、图6为电机在LADRC控制和带有转矩前馈的ADRC 控制下的转矩输出曲线,可得ADRC控制的速度环在负载转矩发生突变时有转矩前馈补偿的作用,其转矩可以迅速跟踪负载转矩,整个曲线趋势相对稳定,超调均差且超调量都比较小,输出曲线比LADRC控制更为平稳。
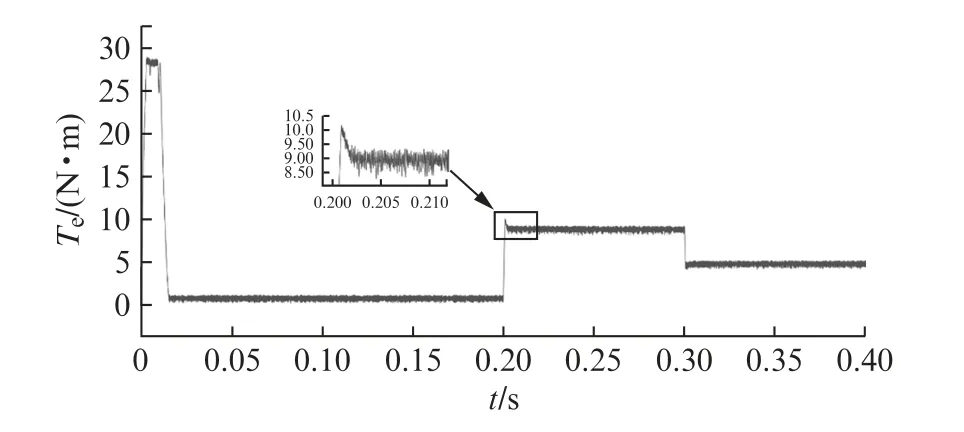
图5 ADRC+负载观测器的转矩曲线
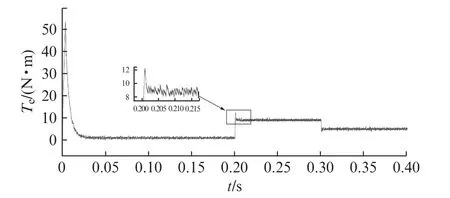
图6 LADRC转矩曲线
6 结 语
通过仿真验证,本文采用的降维负载转矩观测器可以快速准确地跟踪给定转矩值。基于转矩前馈的ADRC控制相较于传统的PI及LADRC控制,在应对转矩突变时,转速波动小、动态性能高、响应时间短、超调均差小且系统稳态性能强,提升了调速系统抗突变的能力,对PMSM 抗负载转矩扰动研究有一定的参考价值。

